Shallow Water Measurements Using a Single Green Laser Corrected by Building a Near Water Surface Penetration Model
Abstract
:1. Introduction
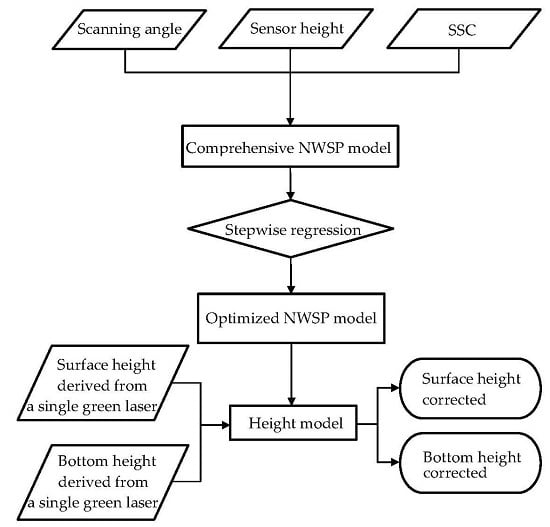
2. Building the NWSP Model
2.1. Comprehensive NWSP Model
2.2. Development of the NWSP Model
2.3. Variable Selection of the NWSP Model
3. Height Models of the Green ALB System
4. Experiment and Analysis
4.1. Data Acquisition
4.2. Construction and Optimization of the NWSP Model
4.3. Height Calculation
4.4. Accuracy Analysis
4.4.1. Accuracy Analysis for the NWSP Models
4.4.2. Accuracy Analysis of the Height Models
5. Discussion
- (1)
- Addition of an assistant IR laser scannerIf an assistant IR laser scanner is mounted on the same platform as the green laser ALB system, the assistant IR laser can provide the reference water surface height. The assistant IR laser scanner is only used prior to the measurement. This scheme was also proposed by Mandlburger et al. [5] and validated to be efficient in various water areas.
- (2)
- Water level of calm waterIf the measured water area (e.g., lakes) is calm, then the reference water surface height can be determined through the water level. The water level can easily be determined, such as through the use of Global Positioning System (GPS) or leveling measurement.
- (1)
- Set the sampling stations with a certain density to ensure that the SSC from these stations can reflect the SSC variations in the water area measured.
- (2)
- Set the stations at the representative locations. Only a few stations are arranged in the water area with small SSC change. By contrast, numerous stations have evident SSC change.
6. Conclusions and Suggestion
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| LiDAR | Light Detection And Ranging |
| ALB | Airborne LiDAR Bathymetry |
| NWSP | Near Water Surface Penetration |
| SSC | Suspended Sediment Concentration |
| CZMIL | Coastal Zone Mapping and Imaging LiDAR |
| EAARL | Experimental Advanced Airborne Research LiDAR |
| GPS | Global Positioning System |
| Probability Density Function | |
| IDW | Inverse Distance Weighting |
| RMSE | Root Mean Square Error |
Appendix A
References
- Guenther, G.C.; Cunningham, A.G.; Laroque, P.E.; Reid, D.J. Meeting the accuracy challenge in airborne Lidar bathymetry. In Proceedings of the 20th EARSeL Symposium: Workshop on Lidar Remote Sensing of Land and Sea, Dresden, Germany, 16–17 June 2000. [Google Scholar]
- Guenther, G.C. Airborne Laser Hydrography: System Design and Performance Factors. Available online: http://shoals.sam.usace.army.mil/downloads/Publications/AirborneLidarHydrography.pdf (accessed on 25 February 2017).
- Maune, D.F. Digital Elevation Model Technologies and Applications: The DEM Users Manual; ASPRS Publications: Annapolis, MD, USA, 2007; pp. 253–320. [Google Scholar]
- Guenther, G.C.; Mesick, H.C. Analysis of airborne laser hydrography waveforms. In Proceedings of the Fourth Laser Hydrography Symposium, Salisbury, Australia, 30 September–3 October 1980. [Google Scholar]
- Mandlburger, G.; Pfennigbauer, M.; Pfeifer, N. Analyzing near water surface penetration in laser bathymetry—A case study at the River Pielach. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Antalya, Turkey, 11–13 November 2013. [Google Scholar]
- Alne, I.S. Topo-Bathymetric Lidar for Hydraulic Modeling-Evaluation of Lidar Data from Two Rivers. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2016. [Google Scholar]
- Quadros, N.D. Unlocking the characteristics of Bathymetric Lidar Sensors. Available online: http://www.lidarmag.com/content/view/10159/199/ (accessed on 18 January 2017).
- Bonisteel, J.M.; Nayegandhi, A.; Wright, C.W.; Brock, J.C.; Nagle, D. Experimental Advanced Airborne Research Lidar (eaarl) Data Processing Manual. Available online: https://pubs.usgs.gov/of/2009/1078/pdf/OFR2009-1078.pdf (accessed on 1 April 2017).
- McKean, J.A.; Isaak, D.J.; Wright, C.W. Geomorphic controls on salmon nesting patterns described by a new, narrow-beam terrestrial–aquatic Lidar. Front. Ecol. Environ. 2008, 6, 125–130. [Google Scholar] [CrossRef]
- McKean, J.; Isaak, D.; Wright, W. Improving stream studies with a small-footprint green Lidar. Trans. Am. Geophys. Union 2009, 90, 341–342. [Google Scholar] [CrossRef]
- McKean, J.; Isaak, D.; Wright, W. Stream and riparian habitat analysis and monitoring with a high-resolution terrestrial-aquatic Lidar. In Proceedings of the Remote Sensing Applications for Aquatic Resource Monitoring, Portland, MD, USA, 28 April–2 May 2008. [Google Scholar]
- McKean, J.; Nagel, D.; Tonina, D.; Bailey, P.; Wright, C.W.; Bohn, C.; Nayegandhi, A. Remote sensing of channels and riparian zones with a narrow-beam aquatic-terrestrial Lidar. Remote Sens. 2009, 1, 1065–1096. [Google Scholar] [CrossRef]
- McKean, J.; Tonina, D.; Bohn, C.; Wright, C. Effects of bathymetric Lidar errors on flow properties predicted with a multi-dimensional hydraulic model. J. Geophys. Res. Earth Surf. 2014, 119, 644–664. [Google Scholar] [CrossRef]
- Nayegandhi, A.; Brock, J.; Wright, C. Small-Footprint, waveform-resolving Lidar estimation of submerged and sub-canopy topography in coastal environments. Int. J. Remote Sens. 2009, 30, 861–878. [Google Scholar] [CrossRef]
- Nayegandhi, A.; Brock, J.C.; Wright, C.W.; O’Connell, M.J. Evaluating a small footprint, waveform-resolving Lidar over coastal vegetation communities. Photogramm. Eng. Remote Sens. 2006, 72, 1407–1417. [Google Scholar] [CrossRef]
- Guenther, G.C.; LaRocque, P.E.; Lillycrop, W.J. Multiple surface channels in Scanning Hydrographic Operational Airborne Lidar Survey (SHOALS) airborne Lidar. Proc. SPIE 1994, 2258, 422–430. [Google Scholar]
- Guenther, G.C. Wind and nadir angle effects on airborne Lidar water surface returns. Proc. SPIE 1986, 637, 277–286. [Google Scholar]
- Mandlburger, G.; Hauer, C.; Wieser, M.; Pfeifer, N. Topo-Bathymetric Lidar for monitoring river morphodynamics and instream habitats—A case study at the pielach river. Remote Sens. 2015, 7, 6160. [Google Scholar] [CrossRef]
- Pierce, J.W.; Fuchs, E.; Nelson, S.; Feygels, V.; Tuell, G. Development of a novel laser system for the CZMIL Lidar. Proc. SPIE 2010. [Google Scholar] [CrossRef]
- Gippel, C.J. Potential of turbidity monitoring for measuring the transport of suspended solids in streams. Hydrol. Processes 1995, 9, 83–97. [Google Scholar] [CrossRef]
- Lewis, J. Turbidity-controlled suspended sediment sampling for runoff-event load estimation. Water Resour. Res. 1996, 32, 2299–2310. [Google Scholar] [CrossRef]
- Grayson, R.; Finlayson, B.L.; Gippel, C.; Hart, B. The potential of field turbidity measurements for the computation of total phosphorus and suspended solids loads. J. Environ. Manag. 1996, 47, 257–267. [Google Scholar] [CrossRef]
- Smith, D.; Davies-Colley, R. If visual clarity is the issue then why not measure it. In Proceedings of the National Monitoring Conference, Madison, MA, USA, 19–23 May 2002. [Google Scholar]
- Mitchell, S.; Burgess, H.; Pope, D. Observations of fine-sediment transport in a semi-enclosed sheltered natural harbour (Pagham Harbour, UK). J. Coast. Res. 2004, 41, 141–147. [Google Scholar]
- Pavanelli, D.; Bigi, A. Indirect methods to estimate suspended sediment concentration: Reliability and relationship of turbidity and settleable solids. Biosyst. Eng. 2005, 90, 75–83. [Google Scholar] [CrossRef]
- Chanson, H.; Takeuchi, M.; Trevethan, M. Using turbidity and acoustic backscatter intensity as surrogate measures of suspended sediment concentration in a small subtropical estuary. J. Environ. Manag. 2008, 88, 1406–1416. [Google Scholar] [CrossRef] [PubMed]
- Bouhdaoui, A.; Bailly, J.-S.; Baghdadi, N.; Abady, L. Modeling the water bottom geometry effect on peak time shifting in Lidar bathymetric waveforms. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1285–1289. [Google Scholar] [CrossRef]
- Carr, D.A. A study of the Target Detection Capabilities of an Airborne Lidar Bathymetry System. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2013. [Google Scholar]
- Stepwise Regression. Available online: http://ncss.wpengine.netdna-cdn.com/wp-content/themes/ncss/ pdf/Procedures/NCSS/Stepwise_Regression.pdf (accessed on 18 January 2017).
- Fuchs, E.; Mathur, A. Utilizing circular scanning in the CZMIL system. Proc. SPIE 2010. [Google Scholar] [CrossRef]
- Stavn, R.H. Lambert-beer law in ocean waters: Optical properties of water and of dissolved/suspended material, optical energy budgets. Appl. Opt. 1988, 27, 222–231. [Google Scholar] [CrossRef] [PubMed]
- Bartier, P.M.; Keller, C.P. Multivariate interpolation to incorporate thematic surface data using inverse distance weighting (idw). Comput. Geosci. 1996, 22, 795–799. [Google Scholar] [CrossRef]
- Lawson, S.; Wiberg, P.; McGlathery, K.; Fugate, D. Wind-driven sediment suspension controls light availability in a shallow coastal lagoon. Estuar. Coasts 2007, 30, 102–112. [Google Scholar] [CrossRef]
- Wu, D.; Hu, G. Interpolation calculation methods for suspended sediment concentration in the yangtze estuary. In Proceedings of the IEEE International Conference on Intelligent Computing and Intelligent Systems, Shanghai, China, 20–22 November 2009. [Google Scholar]
- Thurman, H.V.; Trujillo, A.P. Introductory Oceanography, 10th ed.; Pearson Education: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Conner, J.T.; Tonina, D. Effect of cross-section interpolated bathymetry on 2D hydrodynamic results in a large river. Earth Surf. Process. Landf. 2014, 39, 463–475. [Google Scholar] [CrossRef]
- Gao, J. Bathymetric mapping by means of remote sensing: Methods, accuracy and limitations. Prog. Phys. Geogr. 2009, 33, 103–116. [Google Scholar] [CrossRef]
- Dickey, T.; Lewis, M.; Chang, G. Optical oceanography: Recent advances and future directions using global remote sensing and in situ observations. Rev. Geophys. 2006. [Google Scholar] [CrossRef]
- Dörnhöfer, K.; Göritz, A.; Gege, P.; Pflug, B.; Oppelt, N. Water constituents and water depth retrieval from Sentinel-2a—A first evaluation in an oligotrophic lake. Remote Sens. 2016, 8, 941. [Google Scholar] [CrossRef]
- Gege, P. WASI-2D: A software tool for regionally optimized analysis of imaging spectrometer data from deep and shallow waters. Comput. Geosci. 2014, 62, 208–215. [Google Scholar] [CrossRef]
- Uriel, E. Hypothesis Testing in the Multiple Regression Model. Available online: http://ctu.edu.vn/~dvxe/ econometrics/uriel_chapter4.pdf (accessed on 18 January 2017).
- Keith, T.Z. Multiple Regression and Beyond; Pearson Education: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Miller, J. Statistical significance testing—A panacea for software technology experiments? J. Syst. Softw. 2004, 73, 183–192. [Google Scholar] [CrossRef]
- Hamilton, L.C. Regression with Graphics: A Second Course in Applied Statistics; Brooks/Cole Pub. Co.: Pacific Grove, CA, USA, 1992. [Google Scholar]
- Afifi, A.; May, S.; Clark, V.A. Computer-Aided Multivariate Analysis; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]







| Performance Index | Parameter |
|---|---|
| Operating altitude | 400 m (nominal) |
| Aircraft speed | 140 kts (nominal) |
| Pulse width | 2.2 ns |
| Pulse repetition frequency | 10 kHz |
| Circular scan rate | 27 Hz |
| λ | IR: 1064 nm; green: 532 nm |
| Maximum depth single pulse | Kd·Dmax = 3.75–4.0 daytime (bottom reflectivity >15%) |
| Minimum depth | <0.15 m |
| Depth accuracy | (0.32 + (0.013 depth)²)½ m, 2σ |
| Sounding scope | 0–30 m |
| Horizontal accuracy | (3.5 + 0.05 depth) m, 2σ |
| Sounding density | 2 m × 2 m nominal |
| Scan angle | 20° (fixed off-nadir, circular pattern) |
| Swath width | 294 m (nominal) |
| Sampling Station | SSC of the Surface Layer (mg/L) |
|---|---|
| 1 | 315 |
| 2 | 122 |
| 3 | 134 |
| 4 | 110 |
| 5 | 185 |
| SSC of the Surface Layer C (mg/L) | Sensor Height H (m) | Beam Scanning Angle φ (°) | NWSP Δd (cm) | |
|---|---|---|---|---|
| Max. | 315 | 438 | 23.5 | 39.4 |
| Min. | 110 | 408 | 17.2 | 17.2 |
| Median | 134 | 423 | 20.1 | 28.5 |
| Item | Coefficient (Units) | Comprehensive Model | Optimized Model | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Value | SE | t | p | Value | SE | t | p | ||
| φ | β1 (m·deg−1) | 8.17 × 10−3 | 6.30 × 10−3 | 1.2981 | 0.1942 | 8.44×10−3 | 2.80×10−4 | 30.093 | 0.0000 |
| φ2 | β2 (m·deg−2) | 1.66 × 10−6 | 1.54 × 10−4 | 0.0107 | 0.9913 | ||||
| H | β3 (1) | 8.03 × 10−3 | 6.10 × 10−3 | 1.3160 | 0.1882 | ||||
| H2 | β4 (m−1) | −9.74 × 10−6 | 7.25 × 10−6 | −1.3428 | 0.1793 | −1.9×10−7 | 8.89×10−8 | −2.1574 | 0.0309 |
| C | β5 (m·mg−1·L) | 2.11 × 10−3 | 4.12 × 10−5 | 51.279 | 0.0000 | 2.12×10−3 | 4.09×10−5 | 51.899 | 0.0000 |
| C2 | β6 (m·mg−2·L2) | −4.63 × 10−6 | 8.98 × 10−8 | −51.489 | 0.0000 | −4.65×10−6 | 8.80×10−8 | −52.843 | 0.0000 |
| Constant | β7 (m) | −1.7389 | 1.2734 | −1.3656 | 0.1721 | −5.4×10−2 | 1.73×10−2 | −3.1341 | 0.0017 |
| Parameter in the NWSP Model | φ | H2 | C | C2 |
|---|---|---|---|---|
| 2.74 × 10−1 | −2.35 × 10−2 | 4.314 | −4.144 |
| NWSP Model | Max/cm | Min/cm | Mean/cm | Std./cm |
|---|---|---|---|---|
| Comprehensive model | 10.52 | −9.01 | 0.1 | 3.1 |
| Optimized model | 10.51 | −8.97 | 0.1 | 3.0 |
| Statistic Parameter | Max./cm | Min./cm | Mean/cm | Std./cm |
|---|---|---|---|---|
| Error of the water-surface height model | 19.8 | −20.0 | 1.3 | 5.3 |
| Error of the water-bottom height model | 5.6 | −8.7 | 0.7 | 1.3 |
| Wind Speed in km/h | Average Height in m | Average Wavelength in m | Wave Slope Range in Degrees |
|---|---|---|---|
| 20 | 0.3 | 10.6 | (−3.2, 3.2) |
| 30 | 0.9 | 22.2 | (−4.6, 4.6) |
| 40 | 1.8 | 39.7 | (−5.2, 5.2) |
| 50 | 3.2 | 61.8 | (−5.9, 5.9) |
| 60 | 5.1 | 89.2 | (−6.5, 6.5) |
| 70 | 7.4 | 121.4 | (−7.0, 7.0) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Zhao, X.; Zhang, H.; Zhou, F. Shallow Water Measurements Using a Single Green Laser Corrected by Building a Near Water Surface Penetration Model. Remote Sens. 2017, 9, 426. https://doi.org/10.3390/rs9050426
Zhao J, Zhao X, Zhang H, Zhou F. Shallow Water Measurements Using a Single Green Laser Corrected by Building a Near Water Surface Penetration Model. Remote Sensing. 2017; 9(5):426. https://doi.org/10.3390/rs9050426
Chicago/Turabian StyleZhao, Jianhu, Xinglei Zhao, Hongmei Zhang, and Fengnian Zhou. 2017. "Shallow Water Measurements Using a Single Green Laser Corrected by Building a Near Water Surface Penetration Model" Remote Sensing 9, no. 5: 426. https://doi.org/10.3390/rs9050426
APA StyleZhao, J., Zhao, X., Zhang, H., & Zhou, F. (2017). Shallow Water Measurements Using a Single Green Laser Corrected by Building a Near Water Surface Penetration Model. Remote Sensing, 9(5), 426. https://doi.org/10.3390/rs9050426