A Quantitative Comparison of Total Suspended Sediment Algorithms: A Case Study of the Last Decade for MODIS and Landsat-Based Sensors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset
2.1.1. HydroLight Simulation
2.1.2. Extrapolation of Simulated Dataset
2.1.3. Grouping of Datasets
2.1.4. HydroLight-Derived Reflectance to Sensor Equivalent Reflectance
2.2. TSS Models
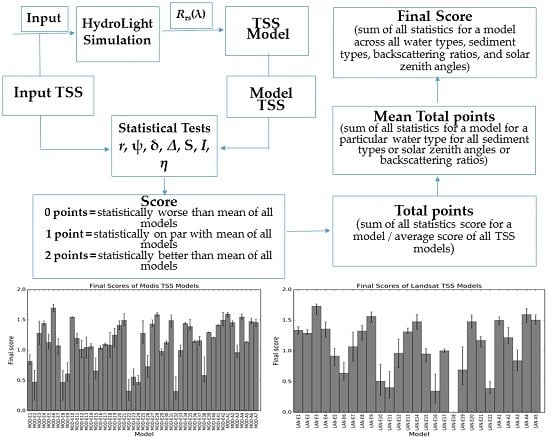
2.3. Statistical Tests and Scoring System
2.3.1. Pearson Correlation Coefficient (r) Test
2.3.2. Root Mean Square Error (ψ) Test
2.3.3. The Bias (δ) Test
2.3.4. The Center-Pattern Root Mean Square Error (Δ) Test
2.3.5. The Slope (S) and Intercept (I) of a Type-2 regression Test
2.3.6. Percentage of Possible Retrievals (η)
2.3.7. Total Points
2.3.8. Mean of Total Points
2.3.9. Final Score
3. Results
3.1. TSS Model Comparisons
3.2. Evaluation of Models
3.2.1. Model Evaluation Using HydroLight Data
3.3.2. Model Evaluation Using In situ Data
4. Discussion
4.1. Data and Methodological Limitation
4.2. TSS Model Selection Guidelines
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Algorithm | Reference | Location | TSS Range (mg/L) | Bands/Algorithms | Regression Coefficient (R2) | Error | N |
|---|---|---|---|---|---|---|---|
| MOD-E1 | Kumar, et al. (2016) [71] | Chilika Lagoon, India | 3.9–161.7 | 0.915 | RMSE = 2.64 mg/L | 54 | |
| MOD-E2 | Ayana, et al. (2015) [40] | Gumera catchment, Lake Tana, Ethiopia | ~5–255 | 0.95 | SE = 10.77 mg/L | 54 | |
| MOD-E3 | Chen, et al. (2015) [22] | Estuary of Yangtze River and Xuwen Coral Reef, China | 5.8–577.2 | 0.752 | RMSE = 2.1 mg/L RMSE = 38.6 mg/l | 40 | |
| MOD-E4 | Zhang, et al. (2016) [72] and Shi, et al. (2015) [21] | Lake Taihu, China | 1.7–343.9 | 0.70 | RMSE = 14.0 mg/L | 150 | |
| MOD-E5 | Choi, et al. (2014) [34] | Mokpo coastal area, Korea | 1.03–193.10 | 0.92 | - | 96 | |
| MOD-E6 | Feng, et al. (2014) [35] | Yangtze estuary | 4.3–1762.1 | 0.88 (low) 0.93 (high) | RMSE = 27.7% | 78 | |
| MOD-E7 | Hudson, et al. (2014) [23] | Fjord in Southwest Greenland | 1.2–716 | 0.84 | - | 143 | |
| MOD-E8 | Kaba, et al. (2014) [31] | Lake Tana, Ethiopia | ~5–255 | 0.95 | RMSE = 16.5 mg/L | 54 | |
| MOD-E9 | Lu, et al. (2014) [73] | Bohai Sea, China | ~<160 | 0.75 | RE ≤ 20% | 627 | |
| MOD-E10 | Park and Latrubesse, (2014) [32] | Amazon River system | 30–150 | 0.88 | RMSE = 6.2 mg/L | 232 | |
| MOD-E11 | Sokoletsky, et al. (2014) [74] | Yangtze river estuary | 0–2500 | - | 361 | ||
| MOD-E12 | Chen, et al. (2014) [61] | Bohai Sea | 4–106.4 | 0.954 | RMS = 30.12% | 48 | |
| MOD-E13 | Cui, et al. (2013) [75] | Ponyang lake, China | 0–141.9 | 0.91 | SE = 11.20 mg/L | 54 | |
| MOD-E14 | Kazemzadeh, et al. (2013) [76] | Bahmanshir River, Iran | 30–500 | 0.63 | RMSE = 261.84 | 23 | |
| MOD-E15 | Raag, et al. (2013) [17] | Pakri Bay, Gulf of Finland | 0–10 | 0.52 | 77 | ||
| MOD-E16 | Qui (2013) [46] | Yellow River Estuary, China | 1.9–1896.5 | 0.95 | MAE = 24.5 mg/L | 81 | |
| MOD-E17 | Villar, et al. (2013) [77] | Maderia River | 25–622 | 0.62 | - | 282 | |
| MOD-E18 | Min, et al. (2012) [78] | Saemangeum coastal area, Korea | 0.1–55 | 0.90 | - | 88 | |
| MOD-E19 | Ondrusek, et al. (2012) [62] | Chesapeake Bay | 4.5–14.92 | 0.95 | MPD = 4.2% | 35 | |
| MOD-E20 | Son and Wang, (2012) [39] | Chesapeake Bay | 1.0–20 | 0.77 | STD = 0.48 | 15,720 | |
| MOD-E21 | Wang, et al. (2012) [60] | Hangzhou Bay, China | 133–1,950 | 0.82 | 35 | ||
| MOD-E22 | Chen, et al. (2011) [24] | Apalachicola Bay, USA | 1.29–208 | 0.86 | RMSE = 4.76 mg/L | 32 | |
| MOD-E23 | Chen, et al. (2011) [36] | Apalachicola Bay, USA | 1.29–208 | 0.8 | RMSE = 4.79 | 25 | |
| MOD-E24 | Jiang and Liu(2011) as cited in [22] | Poyang Lake, China | 0–40 | 0.81 | - | 27 | |
| MOD-E25 | Siswanto, et al. (2011) [79] | Yellow and East China Sea | 0.04–340.07 | 0.92 | RPD = 15.7% | 223 | |
| MOD-E26 | Zhao, et al. (2011) [80] | Mobile Bay estuary, Alabama | 0–87.8 | 0.781 | RMSE = 5.42 | 63 | |
| MOD-E27 | Petus, et al. (2010) [81] and Petus, et al. (2014) [37] | Bay of Biscay, France | 0.3–145.6 | 0.97 | RMSE = 61% | 74 | |
| MOD-E28 | Wang and Lu (2010) [25] | Yangtze River, China | 45–909 | 0.78 | RRMSE = 36.5% | 35 | |
| MOD-E29 | Wang, et al. (2010) [82] | Apalachicola Bay, USA | 1–64 | 0.72 | - | 16 | |
| MOD-E30 | Wang, et al. (2010) [47] | Middle and Lower Yangtze River, China | 75–881 | 0.73 | RMSE = 29.7% | 153 | |
| MOD-E31 | Zhang, et al. (2010) [83] | Yellow and East China Sea | 0.68–27.2 | 0.87 | ARE = 26% | 81 | |
| MOD-E32 | Chen, et al. (2009) [63] | Apalachicola Bay, USA | 1.29–208 | 0.853 | RMSE = 5.5 mg/L | 25 | |
| MOD-E33 | Chu, et al. (2009) [84] | Kangerlussuaq Fjord, Greenland | ~500 | - | - | - | |
| MOD-E34 | Doxaran, et al. (2009L) [85] | Gironde Estuary, France | 77–2182 | 0.89 | RMSE: 18%–22% | 204 | |
| MOD-E35 | Jiang, et al. (2009) [86] | Taihu Lake, China | 0–170 | 0.81 | ARE = 20.5% | 56 | |
| MOD-E36 | Liu and Rossiter (2008) as cited in [22] | Poyang Lake, China | 15.6–518.8 | 0.91 | - | 25 | |
| MOD-E37 | Wang, et al. (2008) [87] | Hangzhou Bay, China | 17–6949 | 0.76 | RMSE = 424 mg/L | 25 | |
| MOD-E38 | Wu and Cui (2008) as cited in [22] | Poyang Lake, China | 0-142 | 0.92 | - | 42 | |
| MOD-E39 | Kutser, et al. (2007) [26] | Muuga and Sillmae Port, Estonia | 2–8 | 0.86 | - | 11 | |
| MOD-E40 | Liu, et al. (2006) [58] | Middle Yangtze River, China | 23.4–61.2 | 0.72 | RE = 34.7% | 41 | |
| MOD-E41 | Sipelgas, et al. (2006) [27] | Parki Bay, Finland | 3–10 | 0.58 | - | 48 | |
| MOD-E42 | Miller and Mckee, (2004) [3] | Northern Gulf of Maxico, USA | 1.0–55.0 | 0.89 | RMSE = 4.74 mg/L | 52 | |
| MOD-A1 | Dorji, et al. (2016) [67] | Onslow, Western Australia | 2.4–69.6 | 0.85 | MARE = 33.33% | 48 | |
| MOD-A2 | Han, et al. (2016) [88] | Europe, French Guiana, Vietnam, North Canada, and China | 0.154–2627 | - | MRAD = 51.9-59% | TSSL = 366 TSSH = 46 | |
| MOD-A3 | Shen, et al. (2014) [89] | Yangtze estuary, China | - | 0.91 | RMSE = 0.0048 (sr−1) | 144 | |
| MOD-A4 | Vanhellemont and Ruddick (2014) [11] | Southern North Sea, UK | 0.5–100 | - | - | - | |
| MOD-A5 | Chen, et al. (2013) [56] | Changjiang River Estuary, China | 70–710 | 0.89 | MRE = 28.99% | 20 | |
| MOD-A6 | Katlane, et al. (2013) [90] | Gulf of Gabes | 0.7–30 | - | - | 56 | |
| MOD-A7 | Nechad, et al. (2010) [38] | Southern North Sea | 1.24–110.27 | 0.80 | RMSE = 11.23 mg/L MRE = 38.9% | 72 | |
| LAN-E1 | Cai, et al. (2015) [91] | Hangzho Bay, China | 203–481 | 0.951 | - | 35 | |
| LAN-E2 | Cai, et al. (2015) [92] | Hangzho, Bay | 179–389.58 | 0.976 | - | 27 | |
| LAN-E3 | Kong, et al. (2015) [7] | Gulf of Bohai Sea | 2.1–208.7 | 0.844 | RMSE = 5.59 | 70 | |
| LAN-E4 | Kong, et al. (2015) [93] | Caofeidian, Bohai Sea | 4.3–104.1 | 0.977 | RMSE = 7.22 mg/L MRE = 25.35 | ||
| LAN-E5 | Lim and Choi (2015) [94] | Nakdong River, South Korea | ~3–14 | 0.74 | RMSE = 1.40 | 48 | |
| LAN-E6 | Wu, et al. (2015) [9] | Dongting Lake, China | 0–63.2 | 0.91 | RMSE = 4.41 mg/L | 52 | |
| LAN-E7 | Zheng, et al. (2015) [95] | Dongting Lake, China | 4.0–101 | 0.82 | MAPE = 21.3% RMSE = 7.01 mg/L | 42 | |
| LAN-E8 | In-Young, et al. (2014) [96] | Old Women Creek Estuary, Ohio, US | 1.0–278 | 0.65 | 11 | ||
| LAN-E9 | Zhang, et al. (2014) [10] | Yellow river estuary | 1.0–1500 | 0.9672 | MRE = 26.1% | 44 | |
| LAN-E10 | Hao, et al. (2013) [97] | Yangtze Estuary, China | ~40.0–750 | 0.8175 | ARE = 36.83 | 17 | |
| LAN-E11 | Hicks, et al. (2013) [98] | Waikato River, New Zealand | 2.0–962 | 0.939 | RMSE = 21.3 | 35 | |
| LAN-E12 | Min, et al. (2013) [78] | Saemangeum coastal area, Korea | 0.1–55 | 0.90 | - | 88 | |
| LAN-E13 | Miller, et al. (2011) [99] | Albemarle-Pamlico Estuarine System, North Carolina, USA | ~5.0–30 | 0.87 | - | 599 | |
| LAN-E14 | Li, et al. (2010) [100] | Changjiang Estuary | ~1.5–560 | 0.915 | - | 21 | |
| LAN-E15 | Wang, et al. (2009) [12] | Yangtze river, China | 22–2610 | 0.88 | MRE = 14.83% | 24 | |
| LAN-E16 | Onderka and Pekarova (2008) [101] | Danube River, Slovakia | 19.5–57.5 | 0.93 | SE = 3.2 mg/L | 10 | |
| LAN-E17 | Teodoro, et al. (2008) [102] | Douro River and Mira Lagoon, Portugal | 14–449 | 0.995 | RMSE = 25.3 mg/L | 11 | |
| LAN-E18 | Aparslan, et al. (2007) [103] | Omerli Dam, Turkey | 0.4–2.9 | 0.99 | SE = 0.0085 mg/L | 6 | |
| LAN-E19 | Wang, et al. (2007) [104] | Yangtze River, China | 0–900 | 0.92 | MAE = 68.9 RMSE = 83.2 | 14 | |
| LAN-E20 | Doxaran, et al. (2006) [105] | Gironde Estuary, France | 10–2000 | 0.88 | SD = 21% | 132 | |
| LAN-E21 | Wang, et al. (2006) [33] | Lake Reelfoot, USA | 11.5–33.5 | 0.52 | - | 18 | |
| LAN-E22 | Zhou, et al. (2006) [15] | Lake Taihu, China | 48.32–120.80 | 0.74 | MPE = 65.40% | ||
| LAN-A1 | Dorji, et al. (2016) [67] | Onslow, Western Australia | 2.4–69.6 | 0.85 | MARE = 33.36% | 48 | |
| LAN-A2 | Han, et al. (2016) [88] | Europe, French Guiana, Vietnam, North Canada, and China | 0.154–2627 | - | MRAD = 51.9%–59% | TSSL = 366 TSSH = 38 | |
| LAN-A3 | Zhang, et al. (2016) [106] | Xinánjiang Resevoir, China | 0.67–5.66 | >0.8 | MRE = 24.3% | 45 | |
| LAN-A4 | Kong, et al. (2015) [7] | Gulf of Bohai Sea | 2.1–208.7 | 0.844 | RMSE = 4.53 | 70 | |
| LAN-A5 | Vanhellemont and Ruddick (2014) [11] | Southern North Sea, UK | 0.5–100 | - | - | - |
Appendix B
| MODEL | Mean Total Score from Sediment | Mean Total Score from Backscattering Ratio (bb/b) | Mean Total Score from Solar Zenith Angles | Final Score | Error Final Score | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | I | II | III | IV | V | I | II | III | IV | V | Lower Bound | Upper Bound | ||
| MOD-E6 | 1.69 | 1.61 | 1.66 | 1.61 | 1.63 | 2.00 | 1.72 | 1.98 | 1.75 | 1.72 | 1.71 | 1.60 | 1.67 | 1.53 | 1.59 | 1.70 | 1.64 | 1.76 |
| MOD-A1 | 1.46 | 1.53 | 1.50 | 1.56 | 1.46 | 1.54 | 1.71 | 1.57 | 1.82 | 1.67 | 1.54 | 1.67 | 1.55 | 1.73 | 1.65 | 1.60 | 1.55 | 1.63 |
| MOD-E28 | 1.53 | 1.51 | 1.53 | 1.51 | 1.51 | 1.71 | 1.71 | 1.71 | 1.74 | 1.71 | 1.52 | 1.55 | 1.52 | 1.51 | 1.56 | 1.59 | 1.56 | 1.63 |
| MOD-A4 | 1.47 | 1.55 | 1.48 | 1.42 | 1.43 | 1.57 | 1.71 | 1.57 | 1.59 | 1.51 | 1.61 | 1.62 | 1.60 | 1.54 | 1.57 | 1.55 | 1.51 | 1.60 |
| MOD-E10 | 1.54 | 1.54 | 1.54 | 1.54 | 1.54 | 1.57 | 1.57 | 1.57 | 1.57 | 1.57 | 1.59 | 1.50 | 1.55 | 1.47 | 1.50 | 1.54 | 1.54 | 1.56 |
| MOD-E42 | 1.48 | 1.49 | 1.46 | 1.42 | 1.47 | 1.57 | 1.16 | 1.57 | 1.76 | 1.57 | 1.61 | 1.17 | 1.60 | 1.51 | 1.62 | 1.50 | 1.40 | 1.63 |
| MOD-E21 | 1.57 | 1.50 | 1.58 | 1.49 | 1.50 | 1.73 | 1.46 | 1.76 | 1.51 | 1.53 | 1.68 | 1.24 | 1.37 | 1.20 | 1.29 | 1.49 | 1.40 | 1.60 |
| MOD-E31 | 1.45 | 1.46 | 1.43 | 1.42 | 1.42 | 1.55 | 1.60 | 1.52 | 1.46 | 1.46 | 1.55 | 1.51 | 1.51 | 1.48 | 1.55 | 1.49 | 1.38 | 1.58 |
| MOD-A6 | 1.47 | 1.46 | 1.49 | 1.42 | 1.40 | 1.43 | 1.57 | 1.43 | 1.57 | 1.43 | 1.47 | 1.54 | 1.49 | 1.50 | 1.47 | 1.48 | 1.44 | 1.53 |
| MOD-A7 | 1.50 | 1.47 | 1.54 | 1.47 | 1.44 | 1.44 | 1.53 | 1.57 | 1.55 | 1.43 | 1.53 | 1.31 | 1.59 | 1.28 | 1.25 | 1.46 | 1.39 | 1.51 |
| MOD-E44 | 1.32 | 1.30 | 1.31 | 1.26 | 1.30 | 1.57 | 1.56 | 1.57 | 1.51 | 1.55 | 1.58 | 1.47 | 1.57 | 1.44 | 1.56 | 1.46 | 1.39 | 1.49 |
| MOD-E27 | 1.38 | 1.42 | 1.37 | 1.41 | 1.41 | 1.46 | 1.57 | 1.47 | 1.57 | 1.54 | 1.49 | 1.33 | 1.49 | 1.27 | 1.35 | 1.44 | 1.38 | 1.50 |
| MOD-E4 | 1.47 | 1.41 | 1.47 | 1.40 | 1.42 | 1.57 | 1.43 | 1.57 | 1.43 | 1.45 | 1.49 | 1.36 | 1.47 | 1.32 | 1.39 | 1.44 | 1.41 | 1.49 |
| MOD-E34 | 1.43 | 1.43 | 1.43 | 1.43 | 1.43 | 1.43 | 1.43 | 1.43 | 1.45 | 1.43 | 1.49 | 1.43 | 1.50 | 1.44 | 1.43 | 1.44 | 1.43 | 1.46 |
| MOD-E41 | 1.41 | 1.40 | 1.41 | 1.40 | 1.41 | 1.43 | 1.43 | 1.43 | 1.43 | 1.43 | 1.46 | 1.34 | 1.45 | 1.32 | 1.46 | 1.41 | 1.41 | 1.43 |
| MOD-E20 | 1.36 | 1.40 | 1.33 | 1.46 | 1.46 | 1.33 | 1.47 | 1.30 | 1.57 | 1.52 | 1.37 | 1.30 | 1.33 | 1.43 | 1.53 | 1.41 | 1.34 | 1.49 |
| MOD-E35 | 1.15 | 1.52 | 1.15 | 1.56 | 1.23 | 1.29 | 1.58 | 1.29 | 1.68 | 1.39 | 1.29 | 1.53 | 1.28 | 1.56 | 1.40 | 1.39 | 1.33 | 1.51 |
| MOD-E39 | 1.31 | 1.31 | 1.31 | 1.31 | 1.31 | 1.28 | 1.29 | 1.29 | 1.29 | 1.29 | 1.31 | 1.26 | 1.30 | 1.25 | 1.31 | 1.29 | 1.29 | 1.30 |
| MOD-E25 | 1.15 | 1.19 | 1.14 | 1.32 | 1.20 | 1.31 | 1.40 | 1.24 | 1.15 | 1.34 | 1.39 | 1.36 | 1.31 | 1.32 | 1.39 | 1.28 | 1.10 | 1.49 |
| MOD-E3 | 0.99 | 1.21 | 0.83 | 1.25 | 1.10 | 1.39 | 1.75 | 1.09 | 1.67 | 1.53 | 1.29 | 1.33 | 1.03 | 1.23 | 1.53 | 1.28 | 1.09 | 1.48 |
| MOD-E19 | 1.39 | 1.22 | 1.42 | 1.26 | 1.24 | 1.30 | 1.12 | 1.40 | 1.36 | 1.14 | 1.38 | 0.90 | 1.43 | 0.98 | 1.22 | 1.25 | 1.05 | 1.36 |
| MOD-E40 | 1.14 | 1.20 | 1.14 | 1.23 | 1.20 | 1.14 | 1.29 | 1.14 | 1.29 | 1.29 | 1.16 | 1.25 | 1.15 | 1.29 | 1.24 | 1.21 | 1.20 | 1.22 |
| MOD-E11 | 1.15 | 1.19 | 1.12 | 1.21 | 1.18 | 1.23 | 1.26 | 1.16 | 1.18 | 1.26 | 1.26 | 1.19 | 1.15 | 1.18 | 1.25 | 1.20 | 1.11 | 1.28 |
| MOD-E37 | 1.13 | 1.09 | 1.13 | 1.09 | 1.10 | 1.24 | 1.22 | 1.25 | 1.27 | 1.23 | 1.14 | 1.11 | 1.14 | 1.11 | 1.14 | 1.16 | 1.08 | 1.23 |
| MOD-E36 | 1.18 | 1.17 | 1.19 | 1.17 | 1.16 | 1.14 | 1.14 | 1.14 | 1.14 | 1.14 | 1.16 | 1.11 | 1.15 | 1.10 | 1.11 | 1.15 | 1.12 | 1.17 |
| MOD-A5 | 1.14 | 1.12 | 1.14 | 1.12 | 1.13 | 1.14 | 1.14 | 1.14 | 1.14 | 1.14 | 1.14 | 1.14 | 1.13 | 1.14 | 1.14 | 1.14 | 1.13 | 1.14 |
| MOD-E5 | 1.30 | 1.16 | 1.32 | 1.18 | 1.19 | 1.19 | 0.90 | 1.20 | 1.08 | 0.96 | 1.33 | 0.94 | 1.22 | 1.01 | 0.97 | 1.13 | 1.02 | 1.26 |
| MOD-E30 | 1.12 | 1.09 | 1.12 | 1.08 | 1.09 | 1.14 | 1.14 | 1.14 | 1.14 | 1.14 | 1.16 | 1.14 | 1.16 | 1.13 | 1.14 | 1.13 | 1.10 | 1.16 |
| MOD-E17 | 1.22 | 1.06 | 1.24 | 1.06 | 1.07 | 1.27 | 1.00 | 1.29 | 1.00 | 1.00 | 1.30 | 0.81 | 1.31 | 0.75 | 1.10 | 1.10 | 1.07 | 1.12 |
| MOD-E18 | 1.23 | 1.12 | 1.08 | 1.05 | 1.11 | 1.32 | 1.16 | 1.12 | 0.84 | 0.92 | 1.47 | 1.01 | 1.28 | 0.71 | 0.88 | 1.09 | 0.88 | 1.30 |
| MOD-E7 | 1.17 | 1.13 | 1.19 | 1.15 | 1.15 | 0.98 | 1.04 | 1.01 | 1.13 | 1.02 | 0.99 | 1.05 | 0.99 | 1.09 | 1.05 | 1.08 | 0.93 | 1.19 |
| MOD-E14 | 1.18 | 1.03 | 1.21 | 1.03 | 1.03 | 1.16 | 1.00 | 1.22 | 1.00 | 1.00 | 1.20 | 0.80 | 1.24 | 0.75 | 1.07 | 1.06 | 1.02 | 1.11 |
| MOD-E13 | 0.85 | 1.02 | 0.82 | 1.08 | 1.03 | 0.84 | 1.25 | 0.81 | 1.41 | 1.28 | 0.97 | 1.11 | 0.93 | 1.17 | 1.16 | 1.05 | 0.87 | 1.22 |
| MOD-E16 | 1.11 | 1.04 | 1.06 | 1.16 | 1.12 | 1.00 | 1.00 | 1.00 | 1.14 | 1.05 | 1.04 | 0.80 | 1.05 | 0.85 | 1.15 | 1.04 | 1.01 | 1.07 |
| MOD-E12 | 1.00 | 1.14 | 1.04 | 1.14 | 1.13 | 0.88 | 1.00 | 0.89 | 1.07 | 1.09 | 0.99 | 0.97 | 0.99 | 1.01 | 0.96 | 1.02 | 0.88 | 1.16 |
| MOD-E33 | 0.94 | 1.03 | 0.91 | 1.07 | 1.03 | 0.90 | 1.10 | 0.82 | 1.14 | 1.12 | 0.93 | 1.02 | 0.88 | 1.03 | 1.07 | 1.00 | 0.90 | 1.09 |
| MOD-E29 | 1.00 | 0.91 | 1.03 | 0.87 | 0.92 | 1.14 | 1.00 | 1.14 | 1.00 | 1.00 | 1.10 | 0.81 | 1.10 | 0.78 | 0.94 | 0.98 | 0.92 | 1.03 |
| MOD-E45 | 0.94 | 1.09 | 0.94 | 1.09 | 0.93 | 0.87 | 1.13 | 0.87 | 1.22 | 0.93 | 0.82 | 0.98 | 0.80 | 0.98 | 0.86 | 0.96 | 0.88 | 1.08 |
| MOD-E1 | 0.91 | 0.85 | 0.92 | 0.84 | 0.86 | 0.76 | 0.72 | 0.78 | 0.72 | 0.72 | 0.82 | 0.82 | 0.85 | 0.83 | 0.86 | 0.82 | 0.77 | 0.93 |
| MOD-E26 | 0.85 | 0.79 | 0.86 | 0.83 | 0.78 | 0.62 | 0.50 | 0.64 | 0.72 | 0.55 | 0.80 | 0.65 | 0.82 | 0.80 | 0.76 | 0.73 | 0.55 | 0.92 |
| MOD-E15 | 0.45 | 0.86 | 0.44 | 0.85 | 0.58 | 0.35 | 0.96 | 0.35 | 0.98 | 0.67 | 0.49 | 0.85 | 0.49 | 0.82 | 0.77 | 0.66 | 0.52 | 0.88 |
| MOD-E9 | 0.60 | 0.71 | 0.59 | 0.75 | 0.73 | 0.48 | 0.49 | 0.47 | 0.58 | 0.56 | 0.68 | 0.57 | 0.68 | 0.67 | 0.60 | 0.61 | 0.49 | 0.80 |
| MOD-E38 | 0.45 | 0.52 | 0.42 | 0.61 | 0.56 | 0.50 | 0.64 | 0.50 | 0.75 | 0.63 | 0.62 | 0.62 | 0.58 | 0.73 | 0.66 | 0.59 | 0.47 | 0.89 |
| MOD-E23 | 0.75 | 0.44 | 0.79 | 0.44 | 0.44 | 0.75 | 0.30 | 0.80 | 0.53 | 0.30 | 0.80 | 0.27 | 0.86 | 0.34 | 0.57 | 0.56 | 0.43 | 0.69 |
| MOD-E8 | 0.51 | 0.41 | 0.51 | 0.35 | 0.48 | 0.62 | 0.60 | 0.59 | 0.24 | 0.55 | 0.60 | 0.44 | 0.56 | 0.24 | 0.40 | 0.47 | 0.18 | 0.67 |
| MOD-E2 | 0.51 | 0.42 | 0.51 | 0.34 | 0.48 | 0.63 | 0.59 | 0.60 | 0.23 | 0.54 | 0.61 | 0.45 | 0.56 | 0.24 | 0.40 | 0.47 | 0.17 | 0.67 |
| MOD-E24 | 0.46 | 0.45 | 0.45 | 0.48 | 0.46 | 0.44 | 0.44 | 0.43 | 0.55 | 0.47 | 0.45 | 0.49 | 0.44 | 0.57 | 0.51 | 0.47 | 0.43 | 0.58 |
| MOD-E22 | 0.44 | 0.23 | 0.54 | 0.32 | 0.24 | 0.31 | 0.11 | 0.42 | 0.37 | 0.16 | 0.46 | 0.09 | 0.58 | 0.25 | 0.40 | 0.33 | 0.17 | 0.52 |
| MOD-E32 | 0.38 | 0.31 | 0.49 | 0.42 | 0.32 | 0.04 | 0.14 | 0.36 | 0.45 | 0.18 | 0.29 | 0.15 | 0.53 | 0.40 | 0.39 | 0.32 | 0.18 | 0.57 |
| MODEL | Mean Total Score from Sediment | Mean Total Score from Backscattering Ratio (bb/b) | Mean Total Score from Solar Zenith Angles | Final Score | Error | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Final Score | ||||||||||||||||||
| I | II | III | IV | V | I | II | III | IV | V | I | II | III | IV | V | Lower Bound | Upper Bound | ||
| LAN-E3 | 1.66 | 1.69 | 1.67 | 1.69 | 1.70 | 1.85 | 1.81 | 1.86 | 1.82 | 1.84 | 1.79 | 1.61 | 1.74 | 1.61 | 1.64 | 1.73 | 1.60 | 1.77 |
| LAN-A4 | 1.54 | 1.63 | 1.54 | 1.63 | 1.64 | 1.62 | 1.69 | 1.64 | 1.71 | 1.67 | 1.59 | 1.50 | 1.56 | 1.48 | 1.50 | 1.60 | 1.46 | 1.69 |
| LAN-E9 | 1.28 | 1.38 | 1.24 | 1.36 | 1.39 | 1.74 | 1.94 | 1.65 | 1.97 | 1.98 | 1.47 | 1.54 | 1.39 | 1.55 | 1.62 | 1.57 | 1.47 | 1.64 |
| LAN-A5 | 1.38 | 1.51 | 1.39 | 1.52 | 1.43 | 1.52 | 1.60 | 1.53 | 1.59 | 1.49 | 1.52 | 1.54 | 1.52 | 1.52 | 1.52 | 1.51 | 1.44 | 1.59 |
| LAN-A1 | 1.33 | 1.53 | 1.34 | 1.58 | 1.45 | 1.54 | 1.69 | 1.46 | 1.80 | 1.63 | 1.52 | 1.27 | 1.48 | 1.33 | 1.59 | 1.50 | 1.43 | 1.56 |
| LAN-E14 | 1.47 | 1.32 | 1.46 | 1.33 | 1.45 | 1.76 | 1.37 | 1.78 | 1.42 | 1.56 | 1.75 | 1.09 | 1.74 | 1.12 | 1.56 | 1.48 | 1.35 | 1.60 |
| LAN-E20 | 1.56 | 1.57 | 1.53 | 1.61 | 1.60 | 1.52 | 1.45 | 1.52 | 1.48 | 1.48 | 1.54 | 1.17 | 1.51 | 1.16 | 1.49 | 1.48 | 1.37 | 1.59 |
| LAN-E4 | 1.53 | 1.42 | 1.42 | 1.33 | 1.58 | 1.41 | 1.54 | 1.46 | 0.91 | 1.45 | 1.51 | 1.21 | 1.46 | 0.68 | 1.50 | 1.36 | 1.23 | 1.48 |
| LAN-E1 | 1.36 | 1.36 | 1.36 | 1.36 | 1.36 | 1.37 | 1.34 | 1.36 | 1.35 | 1.35 | 1.29 | 1.33 | 1.29 | 1.32 | 1.30 | 1.34 | 1.28 | 1.40 |
| LAN-E8 | 1.31 | 1.35 | 1.32 | 1.35 | 1.35 | 1.35 | 1.36 | 1.36 | 1.41 | 1.36 | 1.29 | 1.26 | 1.27 | 1.28 | 1.28 | 1.33 | 1.18 | 1.42 |
| LAN-E13 | 1.36 | 1.39 | 1.38 | 1.35 | 1.37 | 1.30 | 1.28 | 1.35 | 1.27 | 1.30 | 1.35 | 1.20 | 1.35 | 1.12 | 1.35 | 1.31 | 1.28 | 1.37 |
| LAN-E2 | 1.33 | 1.33 | 1.32 | 1.34 | 1.33 | 1.34 | 1.30 | 1.33 | 1.32 | 1.30 | 1.16 | 1.26 | 1.21 | 1.26 | 1.23 | 1.29 | 1.27 | 1.35 |
| LAN-A2 | 1.18 | 1.08 | 1.19 | 1.11 | 1.12 | 1.38 | 1.04 | 1.43 | 1.20 | 1.23 | 1.42 | 1.08 | 1.41 | 1.16 | 1.26 | 1.22 | 1.13 | 1.38 |
| LAN-E21 | 1.16 | 1.11 | 1.20 | 1.10 | 1.11 | 1.28 | 1.13 | 1.43 | 1.01 | 1.08 | 1.25 | 1.16 | 1.40 | 1.05 | 1.15 | 1.17 | 1.07 | 1.24 |
| LAN-E7 | 1.11 | 0.93 | 1.09 | 0.93 | 0.85 | 1.38 | 1.04 | 1.39 | 1.09 | 0.89 | 1.47 | 0.79 | 1.46 | 0.74 | 0.91 | 1.07 | 0.83 | 1.31 |
| LAN-E17 | 1.09 | 1.04 | 1.10 | 1.08 | 1.09 | 1.00 | 0.99 | 1.01 | 1.02 | 1.00 | 0.89 | 0.97 | 0.89 | 0.97 | 0.94 | 1.01 | 0.98 | 1.03 |
| LAN-E12 | 1.13 | 1.02 | 0.96 | 1.12 | 1.24 | 1.09 | 0.74 | 1.11 | 0.61 | 1.05 | 1.25 | 0.71 | 1.19 | 0.50 | 0.75 | 0.96 | 0.73 | 1.20 |
| LAN-E15 | 0.98 | 0.91 | 0.97 | 0.99 | 0.97 | 1.04 | 0.92 | 1.02 | 0.97 | 0.99 | 1.06 | 0.71 | 1.09 | 0.69 | 0.99 | 0.95 | 0.83 | 1.04 |
| LAN-E5 | 0.97 | 0.95 | 0.95 | 0.99 | 0.99 | 0.94 | 0.88 | 0.90 | 0.89 | 0.96 | 0.97 | 0.70 | 0.94 | 0.72 | 1.03 | 0.92 | 0.76 | 1.05 |
| LAN-A3 | 0.93 | 0.93 | 0.90 | 0.93 | 0.89 | 0.92 | 0.85 | 0.88 | 0.66 | 0.61 | 0.92 | 0.91 | 0.90 | 0.72 | 0.69 | 0.84 | 0.68 | 1.02 |
| LAN-E19 | 0.66 | 0.67 | 0.67 | 0.69 | 0.64 | 0.64 | 0.73 | 0.80 | 0.87 | 0.76 | 0.60 | 0.65 | 0.66 | 0.70 | 0.67 | 0.69 | 0.45 | 1.07 |
| LAN-E6 | 0.59 | 0.68 | 0.57 | 0.73 | 0.66 | 0.61 | 0.61 | 0.56 | 0.76 | 0.63 | 0.68 | 0.58 | 0.62 | 0.69 | 0.65 | 0.64 | 0.53 | 0.81 |
| LAN-E10 | 0.42 | 0.45 | 0.39 | 0.45 | 0.45 | 0.65 | 0.59 | 0.61 | 0.65 | 0.48 | 0.66 | 0.44 | 0.60 | 0.44 | 0.36 | 0.51 | 0.28 | 0.78 |
| LAN-E11 | 0.40 | 0.46 | 0.40 | 0.48 | 0.41 | 0.45 | 0.37 | 0.46 | 0.52 | 0.38 | 0.42 | 0.30 | 0.40 | 0.36 | 0.27 | 0.41 | 0.23 | 0.67 |
| LAN-E22 | 0.99 | 0.84 | 1.02 | 0.67 | 0.75 | 0.56 | 0.00 | 0.19 | 0.00 | 0.00 | 0.47 | 0.05 | 0.34 | 0.00 | 0.00 | 0.39 | 0.31 | 0.51 |
| LAN-E16 | 0.29 | 0.20 | 0.30 | 0.30 | 0.31 | 0.43 | 0.30 | 0.43 | 0.42 | 0.45 | 0.36 | 0.27 | 0.41 | 0.32 | 0.44 | 0.35 | 0.16 | 0.62 |
| LAN-E18 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
Appendix C
References
- Bukata, R.P. Applications of water quality products to environmental monitoring. In Satellite Monitoring of Inland and Coastal Water Quality; CRC Press: Boca Raton, FL, USA, 2005; pp. 27–29. [Google Scholar]
- Macdonald, R.K.; Ridd, P.V.; Whinney, J.C.; Larcombe, P.; Neil, D.T. Towards environmental management of water turbidity within open coastal waters of the great barrier reef. Mar. Pollut. Bull. 2013, 74, 82–94. [Google Scholar] [CrossRef] [PubMed]
- Miller, R.L.; McKee, B.A. Using MODIS Terra 250 m imagery to map concentrations of total suspended matter in coastal waters. Remote Sens. Environ. 2004, 93, 259–266. [Google Scholar] [CrossRef]
- Chen, X.; Lu, J.; Cui, T.; Jiang, W.; Tian, L.; Chen, L.; Zhao, W. Coupling remote sensing retrieval with numerical simulation for spm study—Taking bohai sea in China as a case. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S203–S211. [Google Scholar] [CrossRef]
- Havens, K.E.; Beaver, J.R.; Casamatta, D.A.; East, T.L.; James, R.T.; Mccormick, P.; Phlips, E.J.; Rodusky, A.J. Hurricane effects on the planktonic food web of a large subtropical lake. J. Plankton Res. 2011, 33, 1081–1094. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.; Liu, X.; Wang, M.; Qin, B. Remote sensing of diffuse attenuation coefficient of photosynthetically active radiation in lake taihu using MERIS data. Remote Sens. Environ. 2014, 140, 365–377. [Google Scholar] [CrossRef]
- Kong, J.-L.; Sun, X.-M.; Wong, D.; Chen, Y.; Yang, J.; Yan, Y.; Wang, L.-X. A semi-analytical model for remote sensing retrieval of suspended sediment concentration in the Gulf of Bohai, China. Remote Sens. 2015, 7, 5373–5397. [Google Scholar] [CrossRef] [Green Version]
- Chang, N.-B.; Imen, S.; Vannah, B. Remote sensing for monitoring surface water quality status and ecosystem state in relation to the nutrient cycle: A 40-year perspective. Crit. Rev. Environ. Sci. Technol. 2015, 45, 101–166. [Google Scholar] [CrossRef]
- Wu, G.; Cui, L.; Liu, L.; Chen, F.; Fei, T.; Liu, Y. Statistical model development and estimation of suspended particulate matter concentrations with Landsat 8 oli images of Dongting Lake, China. Int. J. Remote Sens. 2015, 36, 343–360. [Google Scholar] [CrossRef]
- Zhang, M.; Dong, Q.; Cui, T.; Xue, C.; Zhang, S. Suspended sediment monitoring and assessment for Yellow River estuary from Landsat TM and ETM + Imagery. Remote Sens. Environ. 2014, 146, 136–147. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Turbid wakes associated with offshore wind turbines observed with Landsat 8. Remote Sens. Environ. 2014, 145, 105–115. [Google Scholar] [CrossRef]
- Wang, J.-J.; Lu, X.X.; Liew, S.C.; Zhou, Y. Retrieval of suspended sediment concentrations in large turbid rivers using Landsat Etm+: An example from the Yangtze River, china. Earth Surf. Process. Landf. 2009, 34, 1082–1092. [Google Scholar] [CrossRef]
- Wu, G.; De Leeuw, J.; Skidmore, A.K.; Prins, H.H.T.; Liu, Y. Comparison of modis and Landsat TM5 images for mapping tempo–Spatial dynamics of secchi disk depths in Poyang Lake national Nature Reserve, China. Int. J. Remote Sens. 2008, 29, 2183–2198. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year landsat water clarity census of Minnesota's 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, S.; Zhou, Y.; Troy, A. Mapping the concentrations of total suspended matter in Lake Taihu, China, using Landsat-5 TM data. Int. J. Remote Sens. 2006, 27, 1177–1191. [Google Scholar] [CrossRef]
- Chen, X.; Han, X.; Feng, L. Towards a practical remote-sensing model of suspended sediment concentrations in turbid waters using meris measurements. Int. J. Remote Sens. 2015, 36, 3875–3889. [Google Scholar] [CrossRef]
- Raag, L.; Uiboupin, R.; Sipelgas, L. Analysis of historical meris and modis data to evaluate the impact of dredging to monthly mean surface tsm concentration. Proc. SPIE 2013. [Google Scholar] [CrossRef]
- Yang, W.; Matsushita, B.; Chen, J.; Fukushima, T. Estimating constituent concentrations in case II waters from meris satellite data by semi-analytical model optimizing and look-up tables. Remote Sens. Environ. 2011, 115, 1247–1259. [Google Scholar] [CrossRef] [Green Version]
- Shen, F.; Verhoef, W.; Zhou, Y.; Salama, M.S.; Liu, X. Satellite estimates of wide-range suspended sediment concentrations in Changjiang (Yangtze) estuary using MERIS data. Estuar. Coast. 2010, 33, 1420–1429. [Google Scholar] [CrossRef]
- Alikas, K.; Reinart, A. Validation of the meris products on large european lakes: Peipsi, Vänern and Vättern. Hydrobiologia 2008, 599, 161–168. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.; Zhu, G.; Liu, X.; Zhou, Y.; Xu, H.; Qin, B.; Liu, G.; Li, Y. Long-term remote monitoring of total suspended matter concentration in Lake Taihu using 250 m Modis-Aqua data. Remote Sens. Environ. 2015, 164, 43–56. [Google Scholar] [CrossRef]
- Chen, S.; Han, L.; Chen, X.; Li, D.; Sun, L.; Li, Y. Estimating wide range total suspended solids concentrations from Modis 250-m imageries: An improved method. ISPRS J. Photogramm. Remote Sens. 2015, 99, 58–69. [Google Scholar] [CrossRef]
- Hudson, B.; Overeem, I.; McGrath, D.; Syvitski, J.P.M.; Mikkelsen, A.; Hasholt, B. Modis observed increase in duration and spatial extent of sediment plumes in greenland fjords. The Cryosphere 2014, 8, 1161–1176. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Huang, W.; Chen, W.; Chen, X. An enhanced modis remote sensing model for detecting rainfall effects on sediment plume in the coastal waters of apalachicola bay. Mar. Environ. Res. 2011, 72, 265–272. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.J.; Lu, X.X. Estimation of suspended sediment concentrations using Terra MODIS: An example from the lower Yangtze River, China. Sci. Total Environ. 2010, 408, 1131–1138. [Google Scholar] [CrossRef] [PubMed]
- Kutser, T.; Metsamaa, L.; Vahtmae, E.; Aps, R. Operative monitoring of the extent of dredging plumes in coastal ecosystems using MODIS satellite imagery. J. Coast. Res 2007, 50, 180–184. [Google Scholar]
- Sipelgas, L.; Raudsepp, U.; Kõuts, T. Operational monitoring of suspended matter distribution using MODIS images and numerical modelling. Adv. Space Res. 2006, 38, 2182–2188. [Google Scholar] [CrossRef]
- Doxaran, D.; Froidefond, J.M.; Lavender, S.; Castaing, P. Spectral signature of highly turbid waters: Application with spot data to quantify suspended particulate matter concentrations. Remote Sens. Environ. 2002, 81, 149–161. [Google Scholar] [CrossRef]
- Ekercin, S. Water quality retrievals from high resolution ikonos multispectral imagery: A case study in Istanbul, Turkey. Water Air Soil Pollut. 2007, 183, 239–251. [Google Scholar] [CrossRef]
- Lim, H.S.; MatJafri, M.Z.; Abdullah, K.; Asadpour, R. A two-band algorithm for total suspended solid concentration mapping using theos data. J. Coast. Res. 2013, 29, 624–630. [Google Scholar] [CrossRef]
- Kaba, E.; Philpot, W.; Steenhuis, T. Evaluating suitability of MODIS-Terra images for reproducing historic sediment concentrations in water bodies: Lake tana, ethiopia. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 286–297. [Google Scholar] [CrossRef]
- Park, E.; Latrubesse, E.M. Modeling suspended sediment distribution patterns of the Amazon River using MODIS data. Remote Sens. Environ. 2014, 147, 232–242. [Google Scholar] [CrossRef]
- Wang, F.; Han, L.; Kung, H.T.; Van Arsdale, R.B. Applications of Landsat-5 TM imagery in assessing and mapping water quality in Reelfoot lake, Tennessee. Int. J. Remote Sens. 2006, 27, 5269–5283. [Google Scholar] [CrossRef]
- Choi, J.-K.; Park, Y.J.; Lee, B.R.; Eom, J.; Moon, J.-E.; Ryu, J.-H. Application of the geostationary ocean color imager (GOCI) to mapping the temporal dynamics of coastal water turbidity. Remote Sens. Environ. 2014, 146, 24–35. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Chen, X.; Song, Q. Influence of the three gorges dam on total suspended matters in the Yangtze estuary and its adjacent coastal waters: Observations from MODIS. Remote Sens. Environ. 2014, 140, 779–788. [Google Scholar] [CrossRef]
- Chen, S.; Huang, W.; Chen, W.; Wang, H. Remote sensing analysis of rainstorm effects on sediment concentrations in apalachicola bay, USA. Ecol. Inform. 2011, 6, 147–155. [Google Scholar] [CrossRef]
- Petus, C.; Marieu, V.; Novoa, S.; Chust, G.; Bruneau, N.; Froidefond, J.-M. Monitoring spatio-temporal variability of the adour river turbid plume (Bay of Biscay, France) with MODIS 250-m imagery. Cont. Shelf Res. 2014, 74, 35–49. [Google Scholar] [CrossRef] [Green Version]
- Nechad, B.; Ruddick, K.G.; Park, Y. Calibration and validation of a generic multisensor algorithm for mapping of total suspended matter in turbid waters. Remote Sens. Environ. 2010, 114, 854–866. [Google Scholar] [CrossRef]
- Son, S.; Wang, M. Water properties in Chesapeake Bay from MODIS-Aqua measurements. Remote Sens. Environ. 2012, 123, 163–174. [Google Scholar] [CrossRef]
- Ayana, E.K.; Worqlul, A.W.; Steenhuis, T.S. Evaluation of stream water quality data generated from MODIS images in modeling total suspended solid emission to a freshwater lake. Sci. Total Environ. 2015, 523, 170–177. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.R.; Yamaguchi, Y.; Ogawa, K. Suspended sediment in the Ganges and Brahmaputra rivers in bangladesh: Observation from TM and AVHRR data. Hydrol. Process. 2001, 15, 493–509. [Google Scholar] [CrossRef]
- Evans, R.; Murray, K.L.; Field, S.; Moore, J.A.Y.; Shedrawi, G.; Huntley, B.G.; Fearns, P.; Broomhall, M.; Mckinna, L.I.W.; Marrable, D. Digitise this! A quick and easy remote sensing method to monitor the daily extent of dredge plumes. PLoS ONE 2012, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.A.; Lan-Wei, W.; Smith, C.J.; Reddy, S.; Lewis, A.; Smith, A. Evaluation of satellite remote sensing for operational monitoring of sediment plumes produced by dredging at hay point, Queensland, Australia. J. Appl. Remote Sens. 2007, 1, 011506–011515. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Sathyendranath, S.; Müller, D.; Brockmann, C.; Deschamps, P.-Y.; Devred, E.; Doerffer, R.; Fomferra, N.; Franz, B.; Grant, M.; et al. The ocean colour climate change initiative: III. A round-robin comparison on in-water bio-optical algorithms. Remote Sens. Environ. 2015, 162, 271–294. [Google Scholar] [CrossRef]
- Curran, P.J.; Novo, E.M.M. The relationship between suspended sediment concentration and remotely sensed spectral radiance: A review. J. Coast. Res. 1988, 4, 351–368. [Google Scholar]
- Qiu, Z. A simple optical model to estimate suspended particulate matter in Yellow River Estuary. Opt. Expr. 2013, 21, 27891–27904. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.-J.; Lu, X.X.; Liew, S.C.; Zhou, Y. Remote sensing of suspended sediment concentrations of large rivers using multi-temporal modis images: An example in the middle and lower Yangtze River, China. Int. J. Remote Sens. 2010, 31, 1103–1111. [Google Scholar] [CrossRef]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic San Diego: San Diego, CA, USA, 1994. [Google Scholar]
- Mobley, C.D.; Sundman, L.K. Hydrolight 4.2 Technical Documentation; Sequoia Scientific, Inc.: Redmond, WA, USA, 2001. [Google Scholar]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.C.; Baker, K.S. Optical properties of the clearest natural waters (200–800 nm). Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef] [PubMed]
- Prieur, L.; Sathyendranath, S. An optical classification of coastal and oceanic waters based on the specific spectral absorption curves of phytoplankton pigments, dissolved organic matter, and other particulate materials1. Limnol. Oceanogr. 1981, 26, 671–689. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Arst, H. Optical Properties and Remote Sensing of Multicomponental Water Bodies; Praxis Publishing Ltd: Chichester, UK, 2003. [Google Scholar]
- Chen, J.; Cui, T.W.; Qiu, Z.F.; Lin, C.S. A semi-analytical total suspended sediment retrieval model in turbid coastal waters: A case study in Changjiang River Estuary. Opt. Expr. 2013, 21, 13018–13031. [Google Scholar] [CrossRef] [PubMed]
- Constantin, S.; Doxaran, D.; Constantinescu, Ș. Estimation of water turbidity and analysis of its spatio-temporal variability in the Danube River Plume (Black Sea) using MODIS satellite data. Cont. Shelf Res. 2016, 112, 14–30. [Google Scholar] [CrossRef]
- Liu, C.D.; He, B.Y.; Li, M.-t.; Ren, X.-y. Quantitative modeling of suspended sediment in middle Changjiang River from MODIS. Chin. Geogr. Sci. 2006, 16, 79–82. [Google Scholar] [CrossRef]
- Hu, C.; Chen, Z.; Clayton, T.D.; Swarzenski, P.; Brock, J.C.; Muller–Karger, F.E. Assessment of estuarine water-quality indicators using MODIS medium-resolution bands: Initial results from Tampa Bay, FL. Remote Sens. Environ. 2004, 93, 423–441. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, B.; Liu, X.; Zhou, G.; Zhao, K. Remote-sensing inversion model of surface water suspended sediment concentration based on in situ measured spectrum in Hangzhou Bay, China. Environ. Earth Sci. 2012, 67, 1669–1677. [Google Scholar] [CrossRef]
- Chen, J.; Tingwei, C.; Zhongfeng, Q.; Changsong, L. A split-window model for deriving total suspended sediment matter from MODIS data in the Bohai Sea. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2611–2618. [Google Scholar] [CrossRef]
- Ondrusek, M.; Stengel, E.; Kinkade, C.S.; Vogel, R.L.; Keegstra, P.; Hunter, C.; Kim, C. The development of a new optical total suspended matter algorithm for the Chesapeake Bay. Remote Sens. Environ. 2012, 119, 243–254. [Google Scholar] [CrossRef]
- Chen, S.; Huang, W.; Wang, H.; Li, D. Remote sensing assessment of sediment re-suspension during hurricane frances in Apalachicola Bay, USA. Remote Sens. Environ. 2009, 113, 2670–2681. [Google Scholar] [CrossRef]
- Glover, D.M.; Jenkins, W.J.; Doney, S.C. Modeling Methods for Marine Science; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Chen, J.; Lee, Z.; Hu, C.; Wei, J. Improving satellite data products for open oceans with a scheme to correct the residual errors in remote sensing reflectance. J. Geophys. Res. 2016. [Google Scholar] [CrossRef]
- Dorji, P.; Fearns, P.; Broomhall, M. A semi-analytic model for estimating total suspended sediment concentration in turbid coastal waters of northern Western Australia using MODIS-Aqua 250 m data. Remote Sens. 2016, 8, 556. [Google Scholar] [CrossRef]
- Albert, A.; Mobley, C.D. An analytical model for subsurface irradiance and remote sensing reflectance in deep and shallow case-2 waters. Opt. Expr. 2003, 11, 2873–2890. [Google Scholar] [CrossRef]
- Du, K.; Lee, Z.; Carder, K.L. Closure between Remote Sens. reflectance and inherent optical properties. Proc. SPIE 2006. [Google Scholar] [CrossRef]
- Passang, D.; Peter, F.; Mark, B. A semi-analytic model for estimating total suspended sediment concentration in turbid coastal waters of Northern Western Australia using MODIS-Aqua 250 m data. Curtin University of Technology: Perth, Australia, 2016. [Google Scholar]
- Kumar, A.; Equeenuddin, S.M.; Mishra, D.R.; Acharya, B.C. Remote monitoring of sediment dynamics in a coastal lagoon: Long-term spatio-temporal variability of suspended sediment in Chilika. Estuar. Coast. Shelf Sci. 2016, 170, 155–172. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, K.; Zhou, Y.; Liu, X.; Qin, B. Monitoring the river plume induced by heavy rainfall events in large, shallow, Lake Taihu using MODIS 250 m imagery. Remote Sens. Environ. 2016, 173, 109–121. [Google Scholar] [CrossRef]
- Lu, J.; Chen, X.; Tian, L.; Zhang, W. Numerical simulation-aided MODIS capture of sediment transport for the Bohai sea in China. Int. J. Remote Sens. 2014, 35, 4225–4238. [Google Scholar] [CrossRef]
- Sokoletsky, L.; Yang, X.; Shen, F. MODIS-based retrieval of suspended sediment concentration and diffuse attenuation coefficient in chinese estuarine and coastal waters. Proc. SPIE 2014. [Google Scholar] [CrossRef]
- Cui, L.; Qiu, Y.; Fei, T.; Liu, Y.; Wu, G. Using remotely sensed suspended sediment concentration variation to improve management of Poyang Lake, China. Lake Reser Manag. 2013, 29, 47–60. [Google Scholar] [CrossRef]
- Kazemzadeh, M.B.; Ayyoubzadeh, S.A.; Moridnezhad, A. Remote sensing of temporal and spatial variations of suspended sediment concentration in Bahmanshir Estuary, Iran. Indian J. Sci. Technol. 2013, 6, 5036–5045. [Google Scholar]
- Espinoza Villar, R.; Martinez, J.-M.; Le Texier, M.; Guyot, J.-L.; Fraizy, P.; Meneses, P.R.; Oliveira, E.d. A study of sediment transport in the madeira river, brazil, using modis remote-sensing images. J. South Am. Earth Sci. 2013, 44, 45–54. [Google Scholar] [CrossRef]
- Min, J.-E.; Ryu, J.-H.; Lee, S.; Son, S. Monitoring of suspended sediment variation using Landsat and MODIS in the Saemangeum Coastal Area of Korea. Mar. Pollut. Bull. 2012, 64, 382–390. [Google Scholar] [CrossRef] [PubMed]
- Siswanto, E.; Tang, J.; Yamaguchi, H.; Ahn, Y.-H.; Ishizaka, J.; Yoo, S.; Kim, S.W.; Kiyomoto, Y.; Yamada, K.; Chiang, C.; et al. Empirical ocean-color algorithms to retrieve chlorophyll-A, total suspended matter, and colored dissolved organic matter absorption coefficient in the Yellow and East China Seas. J. Oceanogr. 2011, 67, 627–650. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, Q.; Walker, N.D.; Zheng, Q.; MacIntyre, H.L. A study of sediment transport in a shallow estuary using MODIS imagery and particle tracking simulation. Int. J. Remote Sens. 2011, 32, 6653–6671. [Google Scholar] [CrossRef]
- Petus, C.; Chust, G.; Gohin, F.; Doxaran, D.; Froidefond, J.M.; Sagarminaga, Y. Estimating turbidity and total suspended matter in the adour river plume (South Bay of Biscay) using MODIS 250-m imagery. Cont. Shelf Res. 2010, 30, 379–392. [Google Scholar] [CrossRef]
- Wang, H.; Hladik, C.M.; Huang, W.; Milla, K.; Edmiston, L.; Harwell, M.A.; Schalles, J.F. Detecting the spatial and temporal variability of chlorophyll—A concentration and total suspended solids in Apalachicola bay, Florida using MODIS imagery. Int. J. Remote Sens. 2010, 31, 439–453. [Google Scholar] [CrossRef]
- Zhang, M.; Tang, J.; Dong, Q.; Song, Q.; Ding, J. Retrieval of total suspended matter concentration in the Yellow and East China Seas from MODIS imagery. Remote Sens. Environ. 2010, 114, 392–403. [Google Scholar] [CrossRef]
- Chu, V.W.; Smith, L.C.; Rennermalm, A.K.; Forster, R.R.; Box, J.E.; Reeh, N. Sediment plume response to surface melting and supraglacial lake drainages on the greenland ice sheet. J. Glaciol. 2009, 55, 1072–1082. [Google Scholar] [CrossRef]
- Doxaran, D.; Froidefond, J.-M.; Castaing, P.; Babin, M. Dynamics of the turbidity maximum zone in a macrotidal estuary (the Gironde, France): Observations from field and MODIS satellite data. Estuar. Coast. Shelf Sci. 2009, 81, 321–332. [Google Scholar] [CrossRef]
- Jiang, X.; Tang, J.; Zhang, M.; Ma, R.; Ding, J. Application of MODIS data in monitoring suspended sediment of Taihu Lake, China. Chin. J. Oceanol. Limnol. 2009, 27, 614–620. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, B.; Xu, J.; Song, L.; Wang, X. Application of neural netword and MODIS 250m imagery for estimating suspended sediments concentration in Hangzhou Bay, China. Environ. Geol. 2008, 56, 1093–1101. [Google Scholar] [CrossRef]
- Han, B.; Loisel, H.; Vantrepotte, V.; Mériaux, X.; Bryère, P.; Ouillon, S.; Dessailly, D.; Xing, Q.; Zhu, J. Development of a semi-analytical algorithm for the retrieval of suspended particulate matter from remote sensing over clear to very turbid waters. Remote Sens. 2016, 8, 211. [Google Scholar] [CrossRef]
- Shen, F.; Zhou, Y.; Peng, X.; Chen, Y. Satellite multi-sensor mapping of suspended particulate matter in turbid estuarine and coastal ocean, China. Int. J. Remote Sens. 2014, 35, 4173–4192. [Google Scholar] [CrossRef]
- Katlane, R.; Nechad, B.; Ruddick, K.; Zargouni, F. Optical remote sensing of turbidity and total suspended matter in the gulf of gabes. Arab. J. Geosci. 2013, 6, 1527–1535. [Google Scholar] [CrossRef]
- Cai, L.; Tang, D.; Li, C. An investigation of spatial variation of suspended sediment concentration induced by a bay bridge based on Landsat Tm and OLI data. Adv. Space Res. 2015, 56, 293–303. [Google Scholar] [CrossRef]
- Cai, L.; Tang, D.; Levy, G.; Liu, D. Remote sensing of the impacts of construction in coastal waters on suspended particulate matter concentration—The case of the Yangtze River Delta, China. Int. J. Remote Sens. 2015, 1–16. [Google Scholar] [CrossRef]
- Kong, J.; Sun, X.; Wang, W.; Du, D.; Chen, Y.; Yang, J. An optimal model for estimating suspended sediment concentration from Landsat Tm images in the Caofeidian Coastal waters. Int. J. Remote Sens. 2015, 36, 5257–5272. [Google Scholar] [CrossRef]
- Lim, J.; Choi, M. Assessment of water quality based on Landsat 8 operational land imager associated with human activities in Korea. Environ. Monit. Asses. 2015, 187, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Li, Y.; Guo, Y.; Xu, Y.; Liu, G.; Du, C. Landsat-based long-term monitoring of total suspended matter concentration pattern change in the wet season for Dongting Lake, China. Remote Sens. 2015, 7, 13975–13999. [Google Scholar] [CrossRef]
- In-Young, Y.; Lang, M.; Vermote, E. Improved understanding of suspended sediment transport process using multi-temporal Landsat data: A case study from the Old Woman Creek Estuary (Ohio). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 636–647. [Google Scholar]
- Hao, J.L.; Cao, T.; Zhang, Z.J.; Yin, L.P. Retrieval and analysis on the sediment concentration of the south branch of the Yangtze Estuary based on TM. Appl. Mech. Mater. 2013, 353–356, 2763–2768. [Google Scholar] [CrossRef]
- Hicks, B.J.; Stichbury, G.A.; Brabyn, L.K.; Allan, M.G.; Ashraf, S. Hindcasting water clarity from Landsat satellite images of unmonitored shallow lakes in the Waikato Region, New Zealand. Environ. Monit. Assess. 2013, 185, 7245–7261. [Google Scholar] [CrossRef] [PubMed]
- Miller, R.L.; Liu, C.-C.; Buonassissi, C.J.; Wu, A.-M. A multi-sensor approach to examining the distribution of total suspended matter (TSM) in the albemarle-pamlico estuarine system, NC, USA. Remote Sens. 2011, 3, 962–974. [Google Scholar] [CrossRef]
- Li, J.; Gao, S.; Wang, Y. Delineating suspended sediment concentration patterns in surface waters of the changjiang estuary by remote sensing analysis. Acta Oceanol. Sin. 2010, 29, 38–47. [Google Scholar] [CrossRef]
- Onderka, M.; Pekárová, P. Retrieval of suspended particulate matter concentrations in the Danube River from Landsat ETM data. Sci. Total Environ. 2008, 397, 238–243. [Google Scholar] [CrossRef] [PubMed]
- Teodoro, A.C.; Veloso-Gomes, F.; Gonçalves, H. Statistical techniques for correlating total suspended matter concentration with seawater reflectance using multispectral satellite data. J. Coast. Res. 2008, 24, 40–49. [Google Scholar] [CrossRef]
- Alparslan, E.; Aydöner, C.; Tufekci, V.; Tüfekci, H. Water quality assessment at ömerli dam using remote sensing techniques. Environ. Monit. Assess. 2007, 135, 391–398. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Lu, X.; Zhou, Y. Retrieval of suspended sediment concentrations in the turbid water of the upper Yangtze River using Landsat ETM+. Chin. Sci. Bull. 2007, 52, 273–280. [Google Scholar] [CrossRef]
- Doxaran, D.; Castaing, P.; Lavender, S.J. Monitoring the maximum turbidity zone and detecting fine-scale turbidity features in the gironde estuary using high spatial resolution satellite sensor (Spot HRV, Landsat ETM+) data. Int. J. Remote Sens. 2006, 27, 2303–2321. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Shi, K.; Zha, Y.; Zhou, Y.; Liu, M. A Landsat 8 oli-based, semianalytical model for estimating the total suspended matter concentration in the slightly turbid Xinanjiang Reservoir (China). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 398–413. [Google Scholar] [CrossRef]





| CHL (mg/m3) | CDOM (m−1) | TSS (mg/L) |
|---|---|---|
| 0.01, 3.0, 20.0 | 0.001, 1.0, 10.0 | 0.01–1.00 at 0.01 interval |
| 1.00–10.00 at 0.1 interval | ||
| 10.00–50.00 at 1.0 interval | ||
| 50.00–100.00 at 2.0 interval | ||
| 100.00–250.00 at 5.0 interval | ||
| 250.00–500.00 at 10.0 interval | ||
| 500.00–2000.00 at 50.0 interval | ||
| 2000.00–7000.00 at 250.0 interval |
| CLASS | CDOM (m−1) | CHL (mg/m3) |
|---|---|---|
| I | 0.01 | 20.0 |
| II | 10.0 | 0.1 |
| III | 10.0 | 20.0 |
| IV | 0.01 | 0.1 |
| V | 1.0 | 5.0 |
| Model | Relative Errors from HydroLight Data Validation | ARE from RRS Uncertainty (%) | ||||
|---|---|---|---|---|---|---|
| SRE (%) | MARE (%) | LRE (%) | −(+) 10% Δ Rrs | −(+) 20% Δ Rrs | −(+) 50% Δ Rrs | |
| MOD-E6 | 59.35 | 94.30 | 139.35 | 70.46 (113.02) | 44.59 (129.11) | 91.94 (170.65) |
| MOD-A1 | 15.00 | 75.56 | 151.14 | 39.24 (126.59) | 38.89 (182.84) | 97.92 (294.93) |
| MOD-E28 | 51.61 | 148.62 | 191.97 | 97.96 (211.76) | 49. 89 (271.68) | 53.30 (497.21) |
| MOD-A4 | 63.14 | 257.59 | 386.87 | 157.51 (346.27) | 68.10 (410.35) | 96.13 (530.23) |
| MOD-E10 | 32.17 | 92.42 | 171.47 | 53.64 (149.97) | 33.54 (242.01) | 49.85 (396.29) |
| MOD-E8 | 189.55 | 220.69 | 344.16 | 244.77 (197.29) | 268.89 (180.18) | 341.16 (164.68) |
| MOD-E2 | 189.55 | 220.69 | 344.16 | 244.77(197.29) | 268.89 180.18() | 341.16 (164.68) |
| MOD-E24 | 77.87 | 141.49 | 218.80 | 10824.61 (9960.40) | 11278.06 (9549.92) | 12747.84 (8416.88) |
| MOD-E22 | 42.31 | 1832.79 | 5403.47 | 2461.87(1149.55) | 1369.44 (1306.50) | 187.31 (1206.94) |
| MOD-E32 | 39.90 | 1717.85 | 6778.93 | 2575.05(1067.58) | 1381.65 (1385.73) | 184.20 (288.28) |
| LAN-E3 | 59.31 | 120.37 | 166.68 | 69.03 (170.14) | 33.14 (220.15) | 76.58 (387.62) |
| LAN-A4 | 57.05 | 197.26 | 266.40 | 134.36 (262.03) | 72.73 (331.63) | 74.29 (541.89) |
| LAN-E9 | 23.52 | 481.82 | 1109.80 | 171.42 (857.00) | 51.00 (1167.00) | 92.43 (1974.47) |
| LAN-A5 | 62.86 | 244.28 | 362.44 | 149. 20 (341.63) | 66. 53 (414.85) | 95.90 (543.85) |
| LAN-A1 | 16.07 | 69.96 | 141.53 | 38.02 (115.85) | 39.00 (169.17) | 97. 78 (286.31) |
| LAN-E10 | 76.17 | 106.43 | 118.16 | 88.74 (126.91) | 82.69 (161.62) | −(357.92) |
| LAN-E11 | 213.54 | 241.28 | 337.58 | 260.07 (22.48) | 278.86 (203.89) | 335.21 (177.52) |
| LAN-E22 | 19.41 | 110.69 | 164.56 | 110. 70 (110.688) | 110. 64 (110.72) | 196.66 (110.60) |
| LAN-E16 | 77.55 | 135.45 | 222.93 | 150.00 (109.18) | 151.20 (103.59) | 223.24 (85.67) |
| LAN-E18 | - | - | - | - | - | - |
| Error/Model | MOD-E10 | MOD-A1 * | MOD-A4 | MOD-E1 | MOD-E38 | LAN-E9 | LAN-A1 * | LAN-A5 | LAN-E6 | LAN-A3 |
|---|---|---|---|---|---|---|---|---|---|---|
| Mare (%) | 46.20 | 33.33 | 100.85 | 341.04 | 256.00 | 43.11 | 33.36 | 102.59 | 55.23 | 35.62 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dorji, P.; Fearns, P. A Quantitative Comparison of Total Suspended Sediment Algorithms: A Case Study of the Last Decade for MODIS and Landsat-Based Sensors. Remote Sens. 2016, 8, 810. https://doi.org/10.3390/rs8100810
Dorji P, Fearns P. A Quantitative Comparison of Total Suspended Sediment Algorithms: A Case Study of the Last Decade for MODIS and Landsat-Based Sensors. Remote Sensing. 2016; 8(10):810. https://doi.org/10.3390/rs8100810
Chicago/Turabian StyleDorji, Passang, and Peter Fearns. 2016. "A Quantitative Comparison of Total Suspended Sediment Algorithms: A Case Study of the Last Decade for MODIS and Landsat-Based Sensors" Remote Sensing 8, no. 10: 810. https://doi.org/10.3390/rs8100810
APA StyleDorji, P., & Fearns, P. (2016). A Quantitative Comparison of Total Suspended Sediment Algorithms: A Case Study of the Last Decade for MODIS and Landsat-Based Sensors. Remote Sensing, 8(10), 810. https://doi.org/10.3390/rs8100810