Early Drought Detection by Spectral Analysis of Satellite Time Series of Precipitation and Normalized Difference Vegetation Index (NDVI)

Abstract

The time lag between anomalies in precipitation and vegetation activity plays a critical role in early drought detection as agricultural droughts are caused by precipitation shortages. The aim of this study is to explore a new approach to estimate the time lag between a forcing (precipitation) and a response (NDVI) signal in the frequency domain by applying cross-spectral analysis. We prepared anomaly time series of image data on TRMM3B42 precipitation (accumulated over antecedent durations of 10, 60, and 150 days) and NDVI, reconstructed and interpolated MOD13A2 and MYD13A2 to daily interval using a Fourier series method to model time series affected by gaps and outliers (iHANTS) for a dry and a wet year in a drought-prone area in the northeast region of China. Then, the cross-spectral analysis was applied pixel-wise and only the phase lag of the annual component of the forcing and response signal was extracted. The 10-day antecedent precipitation was retained as the best representation of forcing. The estimated phase lag was interpreted using maps of land cover and of available soil water-holding capacity and applied to investigate the difference in phenology responses between a wet and dry year. In both the wet and dry year, we measured consistent phase lags across land cover types. In the wet year with above-average precipitation, the phase lag was rather similar for all land cover types, i.e., 7.6 days for closed to open grassland and 14.5 days for open needle-leaved deciduous or evergreen forest. In the dry year, the phase lag increased by 7.0 days on average, but with specific response signals for the different land cover types. Interpreting the phase lag against the soil water-holding capacity, we observed a slightly higher phase lag in the dry year for soils with a higher water-holding capacity. The accuracy of the estimated phase lag was assessed through Monte Carlo simulations and presented reliable estimates for the annual component.

1. Introduction

Every climate zone experiences droughts with impacts varying across regions [1,2]. Drought affects ecosystems and multiple sectors of society, whereas different climate and regional characteristics influence the severity of droughts [3,4]. In this paper, we focus on agricultural drought whereby precipitation shortage leads to decreased vegetation activity [5,6,7].

Since the 1960s, drought-detection systems have been developed to detect and measure the emergence, probability of occurrence and severity of droughts [8,9]. The creation of Drought Early Warning Systems (DEWS) started with the development of drought indices based on meteorological observations. Due to the rapid advancement in earth-observation techniques since the 1970s, a series of remote sensing-derived products can capture most features of the hydrological cycle [10,11,12,13]. Simultaneously, a number of drought indices based on remote sensing products are widely used to monitor the dynamic process of drought events [14,15,16,17]. The inherent advantage of earth observation from space is the capability to capture spatial patterns of multiple indicators of drought at high temporal resolution. DEWS can describe and distinguish particular drought impacts, although the interpretation is constrained to the region for which the DEWS is employed [18]. The drought indices and the effects of drought vary from place to place. The effects of droughts can be mitigated in regions with advanced irrigation systems, or exacerbated due to poor water management and over-grazing [19]. One widely adopted DEWS is based on the combined drought indicator that focuses on the anomalies of precipitation, soil moisture, and vegetation activity, whereby a shortage of rainfall leads to soil moisture deficit and then to reduced biomass production [20].

An important aspect of DEWS is the estimation of the time lag between abnormal precipitation events and its effect on vegetation development reflected by the anomalies in vegetation growth. Within current models, this time lag is estimated by measuring the linear correlation or cross-correlation between changes in two or more drought indicators over time. However, these estimations can lead to poor results as the relationship is affected firstly by random fluctuations, secondly by the influence of the varying growth periods of different vegetation types [21], and thirdly by the magnitude of correlation for different, pre-defined time lags [20,22].

In this study, we applied for the first time conventional cross-spectral analysis techniques to remote sensing data in order to improve the estimation of the time lag, thereby overcoming the need to use predefined lag shifts. Spectral analysis was developed to determine how the total power is distributed in the frequency domain and to detect periodic components in the observed signals by estimating the amplitudes of different periodic components from a signal in the time domain [23,24]. Cross-spectral analysis has been applied in other scientific fields to investigate simultaneously the relationship and corresponding time lags between two stationary time series in the frequency domain [25,26]. Adopting this approach, the time lag is given by the difference in the phase value of the components with high cross-spectral power. Since our precipitation and vegetation activity signals were dominated by the annual component, we focused our analysis on the phase lag of the annual component. This can be regarded as a measure of the causal relationship between forcing (precipitation) and response (vegetation activity). These temporal reaction patterns were interpreted using maps of land cover and of soil water-holding capacity that both are known to influence the time lag [21].

An improved understanding of the sensitivity and temporal response of vegetation to precipitation anomalies would help develop and improve existing preparedness plans to reduce and mitigate the impacts of agricultural droughts. The final objective of this study is to assess and investigate the spatial distribution of the differences in time lag between a dry year with negative precipitation and vegetation activity anomalies and a wet year with positive precipitation and vegetation activity anomalies in a drought-prone region in China.

2. Study Area

A drought-prone region, located between 111°58′E–123°52′E and 40°39′N–49°27′N, centered around Xilinhot in northeastern China was selected for this study (Figure 1a). This region has a complex topography with elevations ranging from 0 to 2120 m, with mountains in the southwest and alluvial plains dominating the central part with a mean annual rainfall of 430 mm/year over the period of 2002 to 2012 [27]. Western Inner Mongolia (Figure 1b) has a 200 mm mean annual precipitation, whereas the Eastern Liaoning province near Shenyang has a mean annual precipitation reaching 800 mm/year. To the northeast of the study region, there is a mean annual precipitation of 600 mm/year. The coefficient of variation of the annual precipitation (Figure 1c) shows that interannual variability of precipitation increases by more than 40% in the Southern Liaoning province near the shoreline of Liaodong Bay, as well as in the west where Inner Mongolia borders with Mongolia. In the northeast and centre of the region, the interannual variability of the precipitation is near or below 20%. The mean annual potential evapotranspiration (ET) in the study area is estimated at 710 mm/year over the period of 2008 to 2013 by applying the method described in Hu and Jia [28]. Higher values were estimated in the south, reaching 1000 mm/year, while the eastern and northern regions have values of 600 mm/year. By comparing the mean annual precipitation with mean annual potential ET over the entire study region, we estimated a mean annual (potential) water deficit of 280 mm/year. The area is characterized by a single crop season, which follows the summer rain season.

Vast portions of the region under study (Figure 2) are covered by sparse vegetation or bare soil. Rain-fed cropland is often surrounded by mixed natural vegetation and crops. Small and scattered irrigated crops occur in the north of Hebei and in the west of Heilongjiang and Jilin provinces. The northeast of the region is covered by needle-leaf deciduous or evergreen forest surrounded by grasslands.

The region is drought prone, experiencing severe and prolonged dry periods since the late 1990s. Both Zou et al. [29] and Yu et al. [30], using the Palmer Drought Severity Index (PDSI) and Standardized Precipitation Evapotranspiration Index (SPEI), respectively, concluded that the significant drying trend in northeast China is striking and unprecedented with droughts in 1982, 1999, 2000, 2001, 2002, 2006 and 2009, with its most extensive drought in 2001 affecting almost 80% of the area. The lower precipitation and above-average air temperature during the summer of 2009 resulted in severe impacts on the vegetation growth [31,32]. In this study, we focus on the dry year of 2009 and the wet year of 2008. In the dry year of 2009 we analyzed the magnitude and lag time of the impact of the negative precipitation anomaly on the negative anomaly in vegetation activity. We compared these results with the same analysis of the positive precipitation anomaly in the wetter year 2008 and the resulting positive anomaly of vegetation activity.

3. Data

3.1. Normalized Difference Vegetation Index (NDVI) Data

As indicators of vegetation activity, we used the Normalized Difference Vegetation Index (NDVI) from MOD13A2 and MYD13A2 data products generated with the radiometric observations collected by the Moderate Resolution Imaging Spectroradiometer (MODIS) on board both the Terra and Aqua satellites [33]. NDVI data was adopted as this region does not face the saturation known in some biomes [34]. The data products MOD13A2 and MYD13A2 are composites over 8 days at a spatial resolution of 1 km. We generated time series of normalized anomaly for the period 1 January 2002–31 December 2012. The years 2008 and 2009 were the wettest and the driest year in this period, respectively, so we focused on these two years for the detailed analysis of vegetation response to precipitation. We used the improved Harmonic ANalysis of Time Series (iHANTS) algorithm, which was updated from the original HANTS described by Menenti, et al. [35] and Verhoef et al. [36], for the time series reconstruction including temporal interpolation and outliers removal in the two MODIS NDVI products. In addition to signal reconstruction, HANTS estimates the amplitude and phase values of periodic components in the observed signal, which is information of direct climatological and phenological relevance. We used the pixel-wise model of time series generated by iHANTS to interpolate the 8-day composites and obtained daily estimates of NDVI. The iHANTS algorithm is a Fourier Transfer based algorithm, widely used for NDVI products. A detailed description of this algorithm including a review of applications can be found in several references [35,36,37,38,39]. A global evaluation of iHANTS performance in the reconstruction of NDVI time series was given by Zhou, et al. [40] and Zhou, et al. [41]. In this study, we analyzed each year separately and applied the four lowest frequency components.

3.2. Precipitation Data

We used the 3B42 data product generated with the observations acquired by the Tropical Rainfall Measuring Mission (TRMM) in the period 1 January 2002–31 December 2012. These daily precipitation estimates have been available since 1998 with an original spatial resolution of 25 km × 25 km. Hu et al. [42] concluded that this product gives the most accurate satellite estimates of rainfall over humid regions in China. We evaluated different durations of antecedent precipitation to understand better the response of vegetation to water availability, particularly the time lag. We retained the daily temporal resolution, but calculated accumulated precipitation over antecedent durations of 10, 60, and 150 days.

3.3. Land Cover and Soils Data

We used as a reference the 2009 global land cover map (ESA GlobCover Project) generated with the radiometric data collected by the Medium Resolution Imaging Spectrometer (MERIS) on board the ENVISAT satellite [43]. The original radiometric data have a spatial resolution of 300 m, which was aggregated to a 1 km spatial resolution for consistency with the precipitation and NDVI data using the majority method. The original land cover map considers 23 different land cover classes of which 14 are present in our study region (Figure 2). Only the seven land cover classes (Figure 3) that have a fractional abundance >1% and together cover 90% of our region were considered for analysis of the results of time series analysis.

The soil water reservoir acts as a buffer in the processes determining vegetation response to precipitation. We used the Available Water Capacity (AWC) of the soils in the study region. The AWC was computed using the difference in soil water content at pressure head of 33 kPa (field capacity) and 1500 kPa (permanent wilting point) determined from the soil water retention curves extracted from the China soil properties database developed by Dai et al. (2013) [44]. The original dataset considers seven soil layers to the depth of 1.38 m. We used the first six layers, i.e., 0–0.05 m, 0.05–0.09 m, 0.09–0.17 m, 0.17–0.29 m, 0.29–0.49 m, 0.49–0.83 m, since Li et al. [45] determined by field investigation that rooting depth of agricultural crops did not exceed 0.80 m in northeast China, and calculated total AWC as:

$${\mathsf{\theta }}_a=\frac{1}{h_{total}}\sum ({\mathsf{\theta }}_{f{c}_n}-{\mathsf{\theta }}_{pw{p}_n})h_n$$

(1)

where ${\mathsf{\theta }}_a$ is the (weighted) mean available water capacity (cm³·cm⁻³); ${\mathsf{\theta }}_{f{c}_n}$ is the field capacity of layer n in cm³·cm⁻³ and ${\mathsf{\theta }}_{pw{p}_n}$ is the permanent wilting point for layer n in cm³·cm⁻³; $h_n$ is the thickness of soil layer n in cm and $h_{total}$ is the total soil depth, i.e., 0.83 m. The spatial resolution of the original dataset is 30 arc-seconds, resampled to a spatial resolution of 1 km using the majority method, so that it is consistent with the other 1 km resolution datasets. Figure 4 describes the estimated available water capacity of the study region.

4. Methods

4.1. NDVI and Precipitation Anomalies

Daily precipitation retrieved from TRMM data was accumulated over the 10 days preceding each NDVI observation; the 10-day cumulative precipitation was used as a measure of available water. We have constructed time series of normalized daily anomalies for vegetation activity and normalized 10-day cumulative precipitation (see Equation (2)). The standard score $z$ of variable $x$ at a pixel ($p$) on day ($d$) of year ($q$) is given by:

$$z_{p,q}\left(d\right)=\frac{x_{p,q}\left(d\right)-\overline{x_{p,q}}}{{\sigma }_{p,q}}$$

(2)

where $\overline{x_{p,q}}$ is the mean at pixel $p$ over the year $q$ , and ${\sigma }_{p,q}$ is the standard deviation at pixel $p$ over the year $q$. Hereafter, $z_i$ is the standard score of 10-day cumulative precipitation and $z_j$ the standard score of daily NDVI. This makes the time series of anomalies at different locations and vegetation cover comparable. The analysis was carried out for each year in the data records.

4.2. Time Lag Estimation in the Frequency Domain

To estimate the time lag in the frequency domain, first the power spectral density (PSD) of both signals is estimated using the multi-taper estimation function. The objective of this method is to estimate the spectrum ($\widehat{f}$) in the frequency ($\omega$) domain by taking $K$ tapers to obtain a set of $K$ eigenspectra including $k$ eigencomponents using time series ($z_i$ and $z_j$) with $N$ data points and constant sampling interval, so that $t=1,2,\dots ,N$. This set of eigenspectra of $z_i$ is defined as follow:

$${\widehat{f}}_{z_i{z}_i}^k\left(\omega \right)={\left|{\sum }_{t=1}^N{z}_i\left(t\right)g_k\left(t\right)e^{-\omega t}\right|}^2$$

(3)

where $g_k\left(t\right)$ is the data taper for the $k$^th eigencomponent and $e^{-\omega t}$ the Fourier transform. The set of data tapers have the shape of Slepian sequences and provide a good protection against leakage. From here, the final multitaper PSD (${\widehat{f}}^{MT}$) is estimated by taking the mean as follows:

$${\widehat{f}}_{z_i{z}_i}^{MT}\left(\omega \right)=\frac{1}{K}{\sum }_{k=1}^K{\widehat{f}}_{z_i{z}_i}^k\left(\omega \right)$$

(4)

where ${\widehat{f}}_{z_i{z}_i}^k\left(\omega \right)$ is the set of $K$ eigenspectra of $z_i$. The cross-spectral density (CSD) estimate is computed using the real valued PSD estimate of $z_i$ defined as ${\widehat{f}}_{z_i{z}_i}^{MT}\left(\omega \right)$ and the complex conjugate of the PSD estimate of $z_j$ defined as ${\widehat{f}}_{z_j{z}_j}^{\ast MT}\left(\omega \right)$ and given by:

$${\widehat{f}}_{z_i{z}_j}^{MT}\left(\omega \right)=\frac{1}{N}{\sum }_{n=1}^N{\widehat{f}}_{z_i{z}_i}^{MT}\left(\omega \right){\widehat{f}}_{z_j{z}_j}^{\ast MT}\left(\omega \right)$$

(5)

The estimate of the coherence $\widehat{C}o{h}_{z_i{z}_j}\left(\omega \right)$ (Equation (6)) indicates how well $z_i$ correspond to $z_j$ at each frequency and is a measure of the strength of the relationship valued between 0 and 1 and defined as:

$$\widehat{C}o{h}_{z_i{z}_j}\left(\omega \right)=\frac{{\left|{\widehat{f}}_{z_i{z}_j}^{MT}\left(\omega \right)\right|}^2}{{\widehat{f}}_{z_i{z}_i}^{MT}\left(\omega \right){\widehat{f}}_{z_j{z}_j}^{MT}\left(\omega \right)}$$

(6)

The phase spectrum estimate ${\phi }_{z_i{z}_j}\left(\omega \right)$ is expressed in units of radian, is bound between −π and π and is the phase difference at each frequency between $z_i$ and $z_j$. It is calculated from the imaginary and real part of the CSD:

$${\phi }_{z_i{z}_j}\left(\omega \right)={\text{tan}}^{-1}\left[\frac{\text{img}{\widehat{f}}_{z_i{z}_j}^{MT}\left(\omega \right)}{\text{real}{\widehat{f}}_{z_i{z}_j}^{MT}\left(\omega \right)}\right]$$

(7)

where $\text{img}{\widehat{f}}_{z_i{z}_j}^{MT}\left(\omega \right)$ is the imaginary part of the CSD and $\text{real}{\widehat{f}}_{z_i{z}_j}^{MT}\left(\omega \right)$ is the real part of the CSD. The time lag ${\phi }_{z_i{z}_j}\left(t\right)$ is expressed in units of days and obtained from the phase spectrum as:

$${\phi }_{z_i{z}_j}\left(t\right)={\phi }_{z_i{z}_j}\left(\omega \right)/\left(2\pi ·\omega \right)$$

(8)

where ${\phi }_{z_i{z}_j}\left(\omega \right)$ is the phase in radian and $\omega$ is the radian frequency. The uncertainty of the phase spectrum is estimated by applying a Monte Carlo simulation. This method adopts a repeated semi-random sampling to obtain the distribution of the phase spectrum. The semi-random time series of $z_i$ and $z_j$ are created as follows:

$$\begin{array}{c}\hfill {z_i}_{rand}\left(t\right)=z_I\left(\omega \right)e^{+\omega t}\hfill \\ \hfill {z_j}_{rand}\left(t\right)=\left(z_J\left(\omega \right)·\sqrt{1-\widehat{C}o{h}_{z_i{z}_j}{\left(\omega \right)}^2}\right)e^{+\omega t}+z_J\left(\omega \right)e^{+\omega t}\hfill \end{array}$$

(9)

where $z_I\left(\omega \right)$ and $z_J\left(\omega \right)$ are the Fourier transforms of the random realizations of the time series divided by the absolute sum of the norm of each realization (as in $z_I\left(\omega \right)={z_i}_n{e}^{-\omega t}$; $z_I\left(\omega \right)=z_I\left(\omega \right)/\sum \left|z_I\left(\omega \right)\right|)$, and $e^{+\omega t}$ represent the inverse Fourier transform. Using these semi-random time series, the phase spectrum is estimated for 100 Monte Carlo simulations and the phase values are estimated at the 95% confidence level.

4.3. Data Processing

The methodology for producing time lag estimates of the annual component is presented in Figure 5. It aims at addressing contamination in NDVI data and preparation of anomaly datasets from the 10 years of precipitation and NDVI data before applying the cross-spectral analysis.

To address the contamination in NDVI, iHANTS was applied to model a time series iteratively using user-selected periodic components. Outliers are identified at each iteration with respect to the current model by applying a user-selected threshold. Noise can be filtered by removing the high frequency and keeping the lower frequency components. Moreover, the reconstruction gives estimates of daily NDVI. We used the four lower frequency components, namely 12-month, 6-month, 4-month and 3-month components. To assess the accuracy of the reconstruction, we did a qualitative check by selecting a pixel from each of the seven dominant land cover types (Figure 6) and observed that the adopted method did capture correctly the phenology response of each land cover type. The areas classified as Rain-fed cropland, mosaic cropland/vegetation, mosaic vegetation/cropland, and open deciduous or evergreen forest have a relatively large increase in NDVI during the summer period, while land cover types—characterised as closed to open herbaceous vegetation, sparse vegetation and bare area—still have a smaller yet clear peak in summer. Abrupt changes in NDVI, such as those due to snowmelt in a short period of time, are difficult to capture by iHANTS, as in April for mosaic vegetation/cropland (Figure 6), at least without using high frequency components.

The cross-spectral analysis was applied to the gap-filled and smoothed time series generated by iHANTS. A denser frequency grid in the frequency domain was obtained through zero-padding and, to accommodate for the limited number of samples in a single year, the sampling rate was increased by repeating the signal to obtain a longer time series [46]. Furthermore, to reduce estimation bias we applied eight independent Slepian sequences as data tapers to the power spectral density of both $z_i$ and $z_j$. The phase spectrum is obtained directly from the CSD, while the time lag of the annual frequency component is obtained by taking the mean phase lag over frequencies within a range of ±5 days (1/360 days~1/370 days) resulting in the frequency band between 0.00270 and 0.00278 Hz. The biannual and higher frequency components are not considered in this study as the precipitation and vegetation activity have both a single annual peak in summer for the selected study region in northeastern China as discussed in Section 2. For areas containing multiple growing seasons, higher frequency components can be of interest as well. The development of the computational code and analysis was done using the Python open-source programming language Nitime library.

5. Results

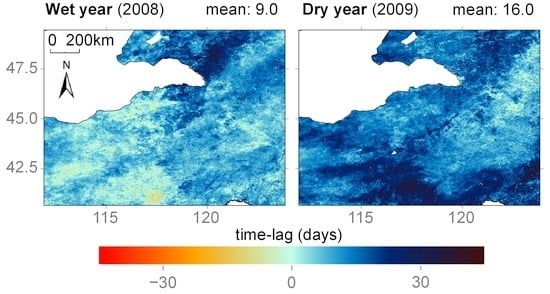
5.1. Temporal Response of Vegetation to Precipitation Anomalies

The time lag is estimated from the multi-taper CSD analysis as explained in Section 4.2. The procedure is illustrated by the intermediate results in Figure 7 using the time series extracted from a random pixel in the study area. We have evaluated the time series of accumulated precipitation described in Section 3.2 and concluded that the 10-day antecedent precipitation characterized best the forcing on vegetation response. Using the cross-spectrum of $z_i$ and $z_j$ the phase spectrum is derived (Equation (7)) and expressed as time lag in days (Equation (8)), where the distribution of the phase spectrum is obtained through a Monte Carlo simulation (Equation (9)). For the pixel considered in this example (Figure 7), the first two components at frequencies of 0.0027 Hz and 0.0055 Hz, have positive power corresponding to the 12-month and 6-month components, respectively (1/0.0027 Hz = 365 days), with a higher power for the 12-month component (Figure 7b), indicating that both periodic components of the two time series are correlated, as shown by the coherence values close to 1 at the same frequencies (Figure 7c). By computing estimates of the phase spectrum, we were then able to analyze the causality between the two time series for all available frequencies. As the region is characterized by single vegetation growth season we focused only on the annual component using a band-pass filter as described in Section 4.3. The phase lag of the annual component for this pixel was 0.54 radian, i.e., a time lag of 31.7 days (Figure 7e,f). This means that the annual component of the normalized vegetation activity anomaly responds with a delay of 31.7 days to the normalized anomaly of the 10-day antecedent precipitation.

As explained in Section 3.2 three durations of antecedent precipitation were evaluated (Figure 8). A longer duration smooths the anomaly time series to yield a better estimate of the amplitude (Figure 8a, 150-day P composite). A shorter duration yields a more complex signal (Figure 8a, 10-day P composite), although the dominant annual component is still observable as was assessed by a qualitative check on the 10-day P composite in Figure 8b. Figure 8a,b suggest that the time lag is positive (NDVI lags P) for the 10-day Ps only, and negative for 60 and 150 days and was verified for the annual components using cross-spectral analysis. The annual component had the strongest power for each duration of antecedent precipitation (Figure 8c–e), where the time lags for the annual component were 16.8, −11.2 and −49.6 days for the 10-, 60- and 150-day Ps, respectively (Figure 8f–h).

Longer duration of antecedent precipitation gives slightly higher cross-power values for the annual component (Figure 8d,e), but the time lag values of the annual component become negative with durations longer than 60 days (Figure 8g,h). Using the 10-day antecedent precipitation we can still capture the cross-power and the time lag for the annual component while the time lag is positive as it should be, i.e., NDVI is expected to lag precipitation, not the other way around. Therefore, we chose the time series of 10-day antecedent precipitation and results presented from now on relate to this dataset only. Clear differences in the time lag were observed in the wet year with positive anomalies and in the dry year with negative anomalies (Figure 9 and

Table 1. Distribution of the time lag of the annual component in the wet year and dry year.

Time Lag (Days)	Wet Year (2008) (%)	Dry Year (2009) (%)
0–10	62	18
10–20	32	57
20–30	5	22
>30	1	3

). Shorter time lags were observed for the wet year with positive anomalies (Figure 9a). In the wet year, the time lag was less than 10 days in 62% of the region and 32% between 10 and 20 days. In the dry year, with negative anomalies, there is a clear shift towards longer time lags (Table 1).

In the dry year, the mean time lag over the entire region was 16 days, i.e., between 10 and 20 days in 57% of the region. In 3% of the region, the time lag was as long as 30 days. In the southern part of the region, the time lag was negligible in the wet year, while a delayed response of vegetation activity was clearly observable in the dry year.

5.2. Stratification by Land Cover and Available Water Capacity

The vulnerability of agricultural crops and natural vegetation changes across species and varieties. Besides genetic traits that determine the response to water stress, the rooting depth in combination with soil water retention buffers the response of vegetation to water availability [21,47]. Accordingly, we have analyzed the observed spatial pattern in time lag (Figure 10) by land cover type (see Figure 2) and taking into account the AWC (Figure 4). In a dry year, with negative anomalies, higher AWC will compensate a below-average precipitation and delay vegetation response. Contrariwise, in a wet year, with positive anomalies, lower AWC will lead earlier past rainfall events to higher soil water potential (i.e., to conditions favourable to plant growth).

To evaluate the dependence of vegetation response to vegetation type and AWC we have first stratified the map of time lag (Figure 9) by land cover type using the seven selected land cover classes that cover 90% of the region (Figure 3). In the dry year, the time lag is longer for all seven land cover classes (Figure 10a), but the temporal response distributions are different as shown by both median and width of each distribution (Figure 10). For rain-fed crops, the median indicates that time lag in the dry year is 10.3 days longer than in the wet year. Overall, the median time lag in the dry year is 18.0 days longer than in the wet year, with a wider spread, as shown by the increase in the interquartile range from 7.3 in the wet year to 10.7 days in the dry one. The interquartile range in rain-fed croplands is 6 days, 41% larger in the dry year, while it decreases from 9.8 days to 6.1 days, 38% in open needle-leaf deciduous or evergreen forest, but with median time lag increasing by 4.8 days. In open grassland, the time lag increases by 9.0 days in the dry year, but the inter-quartile range remains very similar with 7.8 days in the wet and 8.3 days in the dry year. Much smaller is the difference in inter-quartile range for mosaic cropland/vegetation and mosaic vegetation/cropland with 4.4 and 4.3 days, respectively. The near identical response of these two similar classes documents the reliability of the proposed method.

A similar analysis was carried out to evaluate the dependence of time lag on the AWC of the 0–0.5 m soil layer. Overall, in the dry year, longer time lags were observed in the soils with higher AWC. More specifically, the median time lag was 7.4 days in the soils with an AWC between 8.7 and 10.9%, while it was 16.3 days in the soils with the highest AWC, i.e., between 15.4 and 18.9 cm³·cm⁻³. In the wet year, the time lag varies much less across the AWC range of soils in the region: 7.4 days for AWC = 8.7–10.9 cm³·cm⁻³ and 6.8 days for 10.9–12.3 cm³·cm⁻³, respectively. A small increase in the time lag to 8.1 days was estimated for two AWC ranges, i.e., 12.3% to 13.7% and 13.7% to 15.4%. The longest time lag, i.e., 11.6 days, was estimated for the soils with the highest AWC.

6. Discussion

We have presented a novel method to evaluate the causal relationship between two time series of satellite observations on precipitation and vegetation activity in a semi-arid zone with a large difference between precipitation and reference evapotranspiration in summer. The method estimates the time lag for all significant spectral components of the cross-spectral density. We applied this method to satellite precipitation and NDVI data products in northeastern China to investigate the temporal response of vegetation activity to precipitation. Specifically, we analyzed annual time series of standardized anomalies in precipitation and vegetation activity in a wet year (2008) with positive anomalies and a dry year (2009) with negative anomalies. We have evaluated different durations of antecedent precipitation and concluded that a duration of 10 days may not give the highest cross-power amplitude (highest correlation with NDVI anomaly), but could provide reliable estimates of the time lag. Iwasaki [48] used the same cumulative period of 10 days to study the influence of rainfall on NDVI anomaly for a similarly arid region in Mongolia.

6.1. Time Lag Estimations in the Frequency Domain

Numerous studies focused on estimating the time lag of NDVI relative to precipitation [49,50,51,52] or NDVI anomaly relative to precipitation anomaly [22,53]. These authors used cross-correlation analysis in the time domain. The phase-lag method differs from these methods in several ways. Our method is applied in the frequency domain and the phase spectrum provides separate estimates of the phase lag for all the significant spectral components. Noise will appear in the cross-power-spectrum as small amplitude components, which can be filtered out in the frequency domain. Another significant difference is that the amplitude components of the cross-spectrum indicate the causal relationship, while the phase spectrum gives concurrently the phase lag for the corresponding components. This results in the ability of measuring the temporal lag and correlation (causality) simultaneously. Other work on measuring causality such as Granger causality [54,55] and recently, convergent cross-mapping [56] offer an optimized way of detecting the correlation in complex systems. These methods, however, still require an additional method to get robust estimations of the temporal lag between the forcing (precipitation) and response (vegetation activity) signal components that are related to each other.

The novel method to capture and analyze the temporal differences between two time series is based on the decomposition of these time series into multiple frequency components using the Fourier transform. The phase difference computation of two linear time series based on Fourier analysis implicitly assumes that the underlying processes are stationary in time [57]. Cross-spectrum analysis methods can also be applied to signals more complex than the ones analyzed in this study, by taking into account multiple periodic components, e.g., annual and semi-annual in areas where double cropping is widespread. Future research could focus on advanced techniques that might overcome this by using the wavelet transform or the Hilbert-Huang transform. The wavelet transform decomposes a time series into periodic components but determines the temporal variation of the components [58]. The Hilbert-Huang transform is an adaptive analysis method that combines the empirical mode decomposition and the Hilbert spectral analysis to decompose nonlinear and non-stationary processes into intrinsic mode functions resulting in an energy-time-frequency distribution [59].

6.2. Temporal Response in Northeast China

Our results on the northeastern region of China document the feasibility of measuring the response of vegetation activity to precipitation by applying the multi-taper cross-spectral estimation method to time series of satellite observations. To assess this forcing-response relationship, we filtered noise and focused on the most significant periodic component. This study indicates that vegetation activity responds to precipitation anomalies with a time lag of 9.0 days for a wet year (2008) and 16.0 days for a dry year (2009). A similar region in Mongolia was studied [48], and concluded that the temporal lag of the phenological response of grasslands to precipitation is about one month. We have analyzed in detail the time lag in vegetation response for different land cover types and Available (soil) Water Capacity. Overall, the time lag was significantly longer in the dry year, with a clear effect of higher AWC, which gave longer time lags as expected. The analysis by land cover gave less clear-cut indications: time lag in forests was longer than both crops and grasslands, as expected. The slightly longer time lag observed for crops in comparison with grasslands seems to suggest a significant effect of crop management. While we only included land cover types that were significantly represented in the study region (lowest fractional area of land cover type was 4%), influence of mixed pixels in the classification of land cover could have had an influence on the stratification of the time lag maps.

Nezlin et al. [53] and Gessner et al. [22] used time series of absolute anomalies to estimate the temporal lag between anomalies in precipitation and vegetation activity and evaluated their findings by land cover types. Gessner et al. [22] found that in Central Asia the mean time lags of the land cover types “grasslands”, “sparse shrub and sparse herbaceous” and “bare soil” were a maximum of one month in the same order of magnitude as the time lags observed in our study.

For the estimation of the available water capacity, we chose a soil depth corresponding to the dominant rooting depth for the land cover of the region, i.e., a soil depth of 0.80 m. The time lag increases with increasing AWC, but less than linearly. The time lag in open needle-leaf deciduous or evergreen forest was rather similar in the wet and dry year, most likely because of the deeper rooting depth and water uptake in the deeper soil layers as observed by Gessner et al. [22] and Li et al. [60]. In our analysis we focused especially on the effects that occur during the same year; however, for some ecosystems, there is likely also a multi-year lag of soil respiration and forest browning [61]. Additionally, for regions containing multiple growing seasons and/or multiple drying and wetting cycles within a year, multi-annual and/or higher frequency components could have been analyzed with the same methods.

7. Conclusions

We have presented a novel method using the phase spectrum of the cross-spectral density to measure the time lag in the response of vegetation activity to precipitation with the goal of providing useful information to improve early drought detection. An important characteristic of this spectral analysis method is that both the strength of the relationship and the phase lag are determined simultaneously for all significant periodic components. In this study, we determined the cross-power and the phase spectrum of satellite-derived time series on precipitation and NDVI anomalies in a wet and a dry year in a northeast region of China. We found that the time lag was on average 9.0 days in the wet year and 16.0 days in the dry year. We also identified the land cover types where the time lags increased most from the wet to the dry year, i.e., rain-fed croplands, bare soil and open grasslands. The beneficial effect of large Available Water Capacity (15.4–18.9 cm³·cm⁻³) was clearly documented by the small difference in time lag between the wet and dry year (i.e., only 4.7 days). These results provide useful insights on vegetation response to precipitation. As drought originates from a lack of sufficient precipitation, the understanding of the relationship with vegetation activity provides additional information for areas which are more susceptible to drought. More importantly, the corresponding time lag provides valuable information on how vegetation activity responds if there is sufficient precipitation or lack of precipitation.

While much work remains to be done, such as the detection of temporal delay in nonlinear and non-stationary processes, we sense that this method is a valuable addition to current methods of estimating the time lag between time series of satellite observations capturing paired forcing and response signals, as in our case with precipitation and vegetation activity.