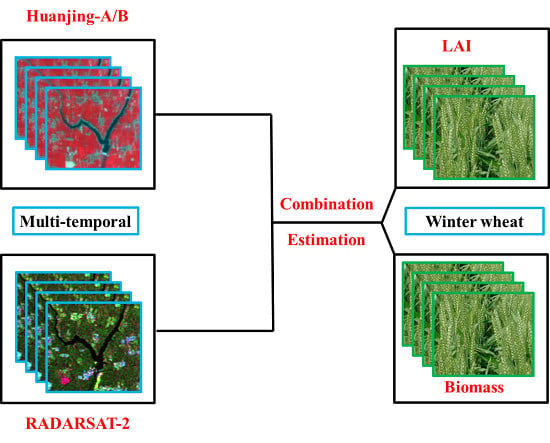
Combined Multi-Temporal Optical and Radar Parameters for Estimating LAI and Biomass in Winter Wheat Using HJ and RADARSAR-2 Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area

2.2. Field Data Measurements
| Date of Samples | Maximum Temperature (°C) | MinimumTemperature (°C) | Precipitation per 24 h (mm) | Relative Humidity (%) | Wind Speed (m/s) | Number of Samples |
|---|---|---|---|---|---|---|
| 4 March 2014 | 13.8 | 5.0 | 0 | 52 | 1.7 | 30 |
| 5 March 2014 | 7.4 | 3.1 | 1.1 | 66 | 1.6 | |
| 28 March 2014 | 20.9 | 9.6 | 0 | 68 | 1.3 | 30 |
| 29 March 2014 | 23.0 | 9.7 | 0 | 56 | 1.6 | |
| 27 April 2014 | 21.6 | 7.9 | 0 | 60 | 1.0 | 30 |
| 28 April 2014 | 23.8 | 8.9 | 0 | 64 | 1.5 | |
| 14 May 2014 | 20.6 | 14.4 | 0 | 67 | 1.5 | 30 |
| 15 May 2014 | 24.5 | 12.2 | 0 | 54 | 1.4 | |
| 16 May 2014 | 21.3 | 13.8 | 0 | 67 | 1.0 | |
| 17 May 2014 | 25.5 | 12.3 | 0 | 64 | 0.7 | |
| 18 May 2014 | 27.6 | 14.3 | 0 | 63 | 1.3 |

| Name | Subset | Samples Size | Min | Mean | Max | Range | SD a | CV b (%) |
|---|---|---|---|---|---|---|---|---|
| LAI | Calibration set | 80 | 0.95 | 3.91 | 6.95 | 6.00 | 1.36 | 34.78 |
| -- | Validation set | 40 | 0.96 | 3.33 | 6.14 | 5.18 | 1.29 | 38.73 |
| Biomass | Calibration set | 80 | 73.89 | 714.67 | 1711.91 | 1638.02 | 400.63 | 56.06 |
| -- | Validation set | 40 | 167.27 | 723.72 | 1634.78 | 1467.51 | 350.24 | 48.39 |
2.3. Satellite Image Preprocessing
2.3.1. Environment and Disaster Monitoring Satellite Constellation (HuanJing-1A/B)
| HJ-1 A/B | ||||||
| Spectral Region (μm) | Spatial Resolution (m) | Orbit Altitude (km) | Swath (km) | |||
| B1: 0.43–0.52 B2: 0.52–0.60 B3: 0.63–0.69 B4: 0.76–0.90 | 30 | 649 | 340 | |||
| RADARSAT-2 | ||||||
| Imaging Mode | Center Frequency | Spatial Resolution (m) | Mean incidence Angle (°) | Orbit Direction | Beam Mode | Resolution Range × Azimuth (m) |
| Fine quad-polarization (HH, HV, VH, VV) | 5.405 GHz (C-band) | 8 | 37 | Ascend | FQ18 | 5.2 × 7.2 |
| Huanjing-1A/B | ||||||
| Date | Scene ID | Acquisition Time (GMT) | Illumination (°) | Path | Row | |
| Sun Zenith | Sun Azimuth | |||||
| 4 March 2014(tillering) | 1182664 | 02:45:12.03 | 38.679 | 317.856 | 15 | 72 |
| 7 April 2014(jointing) | 1190156 | 02:22:15.49 | 47.867 | 300.079 | 7 | 76 |
| 29 April 2014(anthesis) | 1200272 | 02:39:02.22 | 54.754 | 297.400 | 12 | 72 |
| 20 May 2014(filling) | 1208502 | 02:30:07.89 | 56.114 | 283.492 | 8 | 76 |
| RADARSAT-2 | ||||||
| Date | Scene ID | Acquisition Time (GMT) | Illumination (°) | Absolute Orbit | ||
| Incidence Angle | Sun Azimuth | |||||
| 5 March 2014 (tillering) | 313491 | 10:41:46.789 | 27.778 | 349.708 | 32483.0936 | |
| 29 March 2014 (jointing) | 317448 | 10:41:47.153 | 27.777 | 349.710 | 32826.0936 | |
| 22 April 2014 (anthesis) | 321564 | 10:41:47.289 | 27.773 | 349.709 | 33169.0936 | |
| 16 May 2014 (filling) | 325928 | 10:41:47.413 | 27.781 | 349.712 | 33512.0936 | |
2.3.2. RADARSAT-2
2.3.3. Polarization Decomposition Method
2.4. Radar Polarimetric Parameters and Optical Spectral Vegetation Indices Selection
| Vegetation Index | Abbreviation | Formula | Reference |
|---|---|---|---|
| Ratio vegetation index | RVI1# | RNIR/RR | [49] |
| Normalized Difference Vegetation Index | NDVI | (RNIR − RR)/(RNIR + RR) | [50] |
| Soil adjusted vegetation index | SAVI | (1 + L)(RNIR − RR)/(RNIR + RR + L); L = 0.5 | [51] |
| Optimized soil adjusted vegetation index | OSAVI | (RNIR − RR)/(RNIR + RR + 0.16) | [52] |
| Enhanced Vegetation Index | EVI | 2.5(RNIR − RR)/(1 + RNIR + 6RR − 7.5 × RB) | [53] |
| Modified triangular vegetation index 2 | MTVI2 | [18] |
2.5. Method
2.6. Statistical Analysis
3. Results
3.1. Relationships between Optical Spectral Vegetation Indices and LAI, Biomass
| Vegetation Indices | LAI | Biomass | ||||||
|---|---|---|---|---|---|---|---|---|
| Regression Equations | R2 | RMSE | nRMSE (%) | Regression Equations | R2 | RMSE (g/m2) | nRMSE (%) | |
| RVI1 | y = 1.3573x0.7615 | 0.38 ** | 0.77 | 23.21 | y = 77.178x1.596 | 0.51** | 337.35 | 46.61 |
| NDVI | y = 1.1151e2.1763x | 0.39 ** | 0.89 | 26.69 | y = 2898.2x2.401 | 0.55** | 306.40 | 42.34 |
| SAVI | y = 7.317x0.8061 | 0.43 ** | 0.73 | 21.92 | y = 2613.8x1.6528 | 0.58** | 267.25 | 36.95 |
| OSAVI | y = 6.5324x + 0.9519 | 0.43 ** | 0.80 | 24.02 | y = 2573.2x1.696 | 0.62** | 245.63 | 33.93 |
| EVI | y = 6.2125x0.8524 | 0.50 ** | 0.72 | 21.49 | y = 1867.4x1.7007 | 0.68** | 198.65 | 27.44 |
| MTVI2 | y = 5.8067x0.4841 | 0.58 ** | 0.70 | 21.02 | y = 1397.6x0.8554 | 0.63** | 227.41 | 31.42 |
3.2. Relationships between Radar Polarimetric Parameters and LAI, Biomass
| Vegetation Indices | LAI | Biomass | ||||||
|---|---|---|---|---|---|---|---|---|
| Regression Equations | R2 | RMSE | nRMSE (%) | Regression Equations | R2 | RMSE (g/m2) | nRMSE (%) | |
| Entropy | y = 7.5432x − 1.3889 | 0.36** | 1.05 | 31.53 | y = 2515.2x − 988.45 | 0.42** | 297.38 | 41.09 |
| Anisotropy | y = 1.5255ln(x) + 5.4445 | 0.37** | 1.04 | 31.23 | y = 1534.3x0.9401 | 0.44** | 302.45 | 41.79 |
| Alpha | y = 0.3491x0.6558 | 0.33** | 1.06 | 31.83 | y = 1.7927x1.6506 | 0.51** | 288.62 | 39.88 |
| SERD | y = 0.6849e2.3616x | 0.38** | 1.21 | 36.33 | y = 1949.4x3.3077 | 0.58** | 265.01 | 36.31 |
| DERD | y = 1.5644e1.3671x | 0.53** | 0.91 | 27.35 | y = 116.04e2.7989x | 0.71** | 164.21 | 22.70 |
| RVI | y = 0.7202e2.4857x | 0.63** | 0.70 | 21.02 | y = 2518.5x2.8948 | 0.68** | 176.52 | 24.39 |
| HH | y = 13.072x + 1.6461 | 0.52** | 0.99 | 29.73 | y = 4279.6x + 21.069 | 0.63** | 204.82 | 28.30 |
| VV | y = 12.064x + 2.6551 | 0.22** | 2.94 | 88.28 | y = 4312x + 301.59 | 0.27** | 343.25 | 47.43 |
| HV | y = 4.1333e−6.021x | 0.10**. | 3.23 | 96.99 | y = 978.93e−25.4x | 0.11** | 407.14 | 56.26 |
| HH/VV | y = 0.4147x + 2.4973 | 0.46** | 0.96 | 28.83 | y = 133.7x + 261.98 | 0.57** | 234.24 | 32.37 |
| HH/HV | y = 1.3621ln(x) + 0.9885 | 0.42** | 1.01 | 30.33 | y = 108.73x0.8142 | 0.56** | 258.62 | 35.73 |
| VV/HV | y = 2.2514x0.2808 | 0.29** | 1.09 | 32.73 | y = 180.22x0.6895 | 0.51** | 332.02 | 45.88 |
| Vol/Span | y = 5.0295x + 0.8625 | 0.37** | 1.10 | 33.03 | y = 998.53ln(x) + 1272.7 | 0.44** | 356.12 | 49.20 |
| Dbl/Span | y = 0.3357ln(x) + 4.8477 | 0.03n.s. | 3.48 | 104.50 | y = 430.17e3.9395x | 0.03n.s. | 492.46 | 68.05 |
| Odd/Span | y = 3.913x0.0228 | 0.01n.s. | 3.64 | 109.30 | y = 439.07e5.5937x | 0.01n.s. | 596.32 | 82.40 |
3.3. Relationships of Combined Optical Spectral Vegetation Indices and Radar Polarimetric Parameters with Biomass and LAI
| Vegetation Indices | LAI | Biomass | ||||||
|---|---|---|---|---|---|---|---|---|
| Regression Equations | R2 | RMSE | nRMSE (%) | Regression Equations | R2 | RMSE (g/m2) | nRMSE (%) | |
| RVI1 × RVI | y = 2.1548x0.6209 | 0.56** | 0.70 | 20.72 | y = 231.5x1.2164 | 0.72** | 182.42 | 25.20 |
| NDVI × RVI | y = 1.4685e2.4896x | 0.58** | 0.75 | 22.52 | y = 3217.6x1.4544 | 0.77** | 151.27 | 20.90 |
| SAVI × RVI | y = 8.0998x0.6071 | 0.60** | 0.68 | 20.46 | y = 3186.5x1.2003 | 0.76** | 168.31 | 23.26 |
| OSAVI × RVI | y = 8.1476x0.6233 | 0.61** | 0.74 | 22.22 | y = 3163.9x1.2232 | 0.77** | 155.65 | 20.51 |
| EVI × RVI | y = 6.9326x°.5973 | 0.64** | 0.67 | 20.12 | y = 2394.4x1.1858 | 0.80** | 146.33 | 20.21 |
| MTVI2 × RVI | y = 6.2472x0.3814 | 0.68** | 0.65 | 19.52 | y = 1816.2x0.7426 | 0.75** | 170.58 | 23.57 |
| RVI1 × DERD | y = 2.037e0.2308x | 0.52** | 0.75 | 22.52 | y = 190.5e0.4714x | 0.71** | 201.47 | 27.84 |
| NDVI × DERD | y = 1.8016e1.992x | 0.56** | 0.80 | 24.02 | y = 151.66e4.1117x | 0.79** | 159.52 | 22.04 |
| SAVI × DERD | y = 1.9088e2.2375x | 0.58** | 0.70 | 20.72 | y = 174.92e4.4701x | 0.76** | 161.21 | 22.28 |
| OSAVI × DERD | y = 1.896e2.2107x | 0.60** | 0.72 | 21.62 | y = 171.94e4.404x | 0.79** | 148.65 | 20.54 |
| EVI × DERD | y = 1.848e1.8344x | 0.62** | 0.78 | 23.42 | y = 171.25e3.5926x | 0.78** | 156.67 | 21.65 |
| MTVI2 × DERD | y = 6.1902x + 2.0154 | 0.67** | 0.68 | 20.46 | y = 1781.2x + 216.35 | 0.72** | 178.43 | 24.65 |

3.4. Estimation of LAI and Biomass Using Multiple Stepwise Regression (MSR) and Partial Least Squares Regression (PLSR) Methods
| Methods | LAI | Biomass | ||||||
|---|---|---|---|---|---|---|---|---|
| Variables | R2 | RMSE | nRMSE (%) | Variables | R2 | RMSE (g/m2) | nRMSE (%) | |
| Multiple Stepwise regression | EVI × RVI, MTVI2 × DERD | 0.73** | 0.64 | 19.22 | SAVI × RVI, OSAVI × DERD, MTVI2 × DERD | 0.81** | 142.63 | 19.71 |
| Partial least squares regression | 12 COSVI-RPPs | 0.76** | 0.61 | 18. 31 | 12 COSVI-RPPs | 0.85** | 137.21 | 18.96 |
| Multiple stepwise regression | EVI, DERD, EVI × RVI, MTVI2 × DERD | 0.74 | 0.63 | 18.92 | MTVI2, DERD, SAVI × RVI, OSAVI × DERD, MTVI2 × DERD, | 0.83** | 140.34 | 19.39 |
| Partial least squares regression | 12 COSVI-RPPs, 6 OSVIs, 15 RPPs | 0.78 | 0.58 | 17.42 | 12 COSVI-RPPs, 6 OSVIs, 15 RPPs | 0.87** | 134.68 | 18.61 |


4. Discussion
5. Conclusion
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Scharf, P.C.; Lory, J.A. Calibrating corn color from aerial photographs to predict side-dress nitrogen need. Agron. J. 2002, 94, 397–404. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Molden, D.J.; Makin, I.W. Remote sensing for irrigated agriculture examples from research and possible applications. Agr. Water Manage. 2000, 46, 137–155. [Google Scholar] [CrossRef]
- Hunsaker, D.J.; Barnes, E.M.; Clarke, T.R.; Fitzgerald, G.J.; Pinter, P.J. Cotton irrigation scheduling using remotely sensed and FAO-56 basal crop coefficients. Trans. ASAE 2005, 48, 1395–1407. [Google Scholar] [CrossRef]
- Luedeling, E.; Hale, A.; Zhang, M.; Bentley, W.J.; Dharmasri, L.C. Remote sensing of spider mite damage in California peach orchards. Int. J. Appl. Earth Obs. 2009, 11, 244–255. [Google Scholar]
- Mahlein, A.K.; Oerke, E.C.; Steiner, U.; Dehne, H.W. Recent advances in sensing plant diseases for precision crop protection. Eur. J. Plant. Pathol. 2012, 133, 197–209. [Google Scholar] [CrossRef]
- Groten, S.M.E. NDVI-crop monitoring and early yield assessment of Burkina Faso. Int. J. Remote Sens. 1993, 14, 1495–1515. [Google Scholar] [CrossRef]
- Mkhabela, M.S.; Bullock, P.; Raj, S.; Wang, S.; Yang, Y. Crop yield forecasting on the Canadian Prairies using MODIS NDVI data. Agr. Forest Meteorol. 2011, 151, 385–393. [Google Scholar] [CrossRef]
- Dente, L.; Satalino, G.; Mattia, F.; Rinaldi, M. Assimilation of leaf area index derived from ASAR and MERIS data into CERES-wheat model to map wheat yield. Remote Sens. Environ. 2008, 112, 1395–1407. [Google Scholar] [CrossRef]
- Bala, S.K.; Islam, A.S. Correlation between potato yield and MODIS-derived vegetation indices. Int. J. Remote Sens. 2009, 30, 2491–2507. [Google Scholar] [CrossRef]
- Li, X.C.; Zhang, Y.J.; Luo, J.H.; Jin, X.L.; Xu, Y.; Yang, W.Z. Quantification winter wheat LAI with HJ-1CCD image features over multiple growing seasons. Int. J. Appl. Earth Obs. 2015, 44, 104–112. [Google Scholar] [CrossRef]
- Koppe, W.; Gnyp, M.L.; Hennig, S.D.; Li, Fei.; Miao, Y.X.; Chen, X.P.; Jia, L.L.; Bareth, G. Multi-temporal hyperspectral and radar remote sensing for estimating winter wheat biomass in the North China Plain. Photogramm. Fernerkund. Geoinf. 2012, 2012, 281–298. [Google Scholar] [CrossRef]
- Chen, P.; Tremblay, N.; Wang, J.; Vigneaulta, P. New index for crop canopy fresh biomass estimation. Spectrosc. Spect. Anal. 2010, 30, 512–517. [Google Scholar]
- Liu, J.; Pattey, E.; Miller, J.R.; McNairn, H.; Smith, A.; Hu, B. Estimating crop stresses, aboveground dry biomass and yield of corn using multi-temporal optical data combined with a radiation use efficiency model. Remote Sens. Environ. 2010, 114, 1167–1177. [Google Scholar] [CrossRef]
- Liu, J.; Pattey, E.; Jégo, J.R.G. Assessment of vegetation indices for regional crop green LAI estimation from Landsat images over multiple growing seasons. Remote Sens. Environ. 2012, 123, 347–358. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.; Gitelson, A.; Peng, Y.; Vina, A.; Arkebauer, T.; Rundquist, D. Green leaf area index estimation in maize and soybean: Combining vegetation indices to achieve maximal sensitivity. Agron. J. 2012, 104, 1336–1347. [Google Scholar] [CrossRef]
- Jin, X.L.; Diao, W.Y.; Xiao, C.H.; Wang, F.Y.; Chen, B.; Wang, K.R.; Li, S.K. Estimation of wheat agronomic parameters using new spectral indices. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyper-spectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Liu, J.; Pattey, E.; Shang, J.; Admira, S.; Jégo, G.; McNairn, H.; Smith, A.; Hu, B.; Zhang, F.; Freementle, J. Quantifying crop biomass accumulation using multi-temporal optical remote sensing observations. In Proceedings of the 30th Canadian Symposium on Remote Sensing, Lethbridge, AB, Canada, 22–25 June 2009.
- Vina, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of different vegetation indices for the remote assessment of green leaf area index of crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Ramoelo, A.; Skidmore, A.K.; Cho, M.A.; Schlerf, M.; Mathieu, R.; Heitkönig, I.M.A. Regional estimation of savanna grass nitrogen using the red-edge band of the spaceborne RapidEye sensor. Int. J. Appl. Earth Obs. 2012, 19, 151–162. [Google Scholar] [CrossRef]
- Tang, S.; Chen, J.M.; Zhu, Q.; Li, X.; Chen, M.; Sun, R.; Zhou, Y.; Deng, F.; Xie, D. LAI inversion algorithm based on directional reflectance kernels. J. Environ. Manage. 2007, 85, 638–648. [Google Scholar] [CrossRef] [PubMed]
- Ulaby, F.; Moore, R.; Fung, A. Microwave Remote Sensing: From Theory to Applications; Artech House Publishers: Norwood, MA, USA, 1986. [Google Scholar]
- Gao, S.; Niu, Z.; Huang, N.; Hou, X.H. Estimating the leaf area index, height and biomass of maize using HJ-1 and RADARSAT-2. Int. J. Appl. Earth Obs. 2013, 24, 1–8. [Google Scholar] [CrossRef]
- eoPortal Directory. Satellite Missions Database. Available online: https://directory.eoportal.org/web/eoportal/satellite-missions (accessed on 21 August 2015).
- Global Monitoring for Environment and Security (GMES)-Observing the Earth. Synthetic Aperture Radar Missions. Available online: http://www.esa.int/Our_Activities/Observing_the_Earth/GMES/SAR_missions (accessed on 21 August 2015).
- Capodici, F.; D’Urso, G.; Maltese, A. Investigating the Relationship between X-Band SAR Data from COSMO-SkyMed Satellite and NDVI for LAI Detection. Remote Sens. 2013, 5, 1389–1404. [Google Scholar] [CrossRef] [Green Version]
- Cutler, M.E.J.; Boyd, D.S.; Foody, G.M.; Vetrivel, A. Estimating tropical forest biomass with a combination of SAR image texture and Landsat TM data: An assessment of predictions between regions. ISPRS J. Photogramm. Remote Sens. 2012, 70, 66–77. [Google Scholar] [CrossRef] [Green Version]
- Imhoff, M.L. Radar backscatter and biomass saturation: Ramifications for global biomass inventory. IEEE Trans. Geosci. Remote Sens. 1995, 33, 511–518. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Rauste, Y. Multi-temporal JERS SAR data in boreal forest mapping. Remote Sens. Environ. 2005, 97, 263–275. [Google Scholar] [CrossRef]
- Castel, T.; Guerra, F.; Caraglio, Y.; Houllier, F. Retrieval biomass of a large Venezuelan pine plantation using JERS-1 SAR data-Analysis of forest structure impact on radar signature. Remote Sens. Environ. 2002, 79, 30–41. [Google Scholar] [CrossRef]
- Lucas, R.M.; Cronin, N.; Lee, A.; Moghaddam, M.; Witte, C.; Tickle, P. Empirical relationships between AIRSAR backscatter and LiDAR-derived forest biomass, Queensland, Australia. Remote Sens. Environ. 2006, 100, 407–425. [Google Scholar] [CrossRef]
- Lucas, R.M.; Cronin, N.; Moghaddam, M.; Lee, A.; Armston, J.; Bunting, P.; Witte, C. Integration of radar and Landsat-derived foliage projected cover for woody regrowth mapping, Queensland, Australia. Remote Sens. Environ. 2006, 100, 388–406. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Vanleeuwen, H.J.C. Combined use of optical and microwave remote sensing data for crop growth monitoring. Remote Sens. Environ. 1996, 56, 42–51. [Google Scholar] [CrossRef]
- Manninen, T.; Smolander, H.; Voipio, P.; Stenberg, P.; Rautiainen, M.; Ahola, H. Boreal forest LAI retrieval using both optical and microwave data of ENVISAT. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 25–29 July 2005.
- Kar, G.; Verma, H.N.; Singh, R. Effect of winter crop and supplementary irrigation on crop yield, water use efficiency and profitability in rainfed rice based on cropping system of eastern India. Agr. Water Manage. 2006, 79, 280–292. [Google Scholar] [CrossRef]
- Dettwiler, M. Radarsat-2 Product Format Definition; Macdonald, Dettwiler and Associates Ltd.: Richmond, BC, Canada, 2008. [Google Scholar]
- Koppe, W.; Gnyp, M.L.; Hütt, C.; Yao, Y.; Miao, Y.; Chen, X.; Bareth, G. Rice monitoring with multi-temporal and dual-polarimetric TerraSAR-X data. Int. J. Appl. Earth Obs. 2013, 21, 568–576. [Google Scholar] [CrossRef]
- Johnstone, I.M.; Raimondo, M. Periodic boxcar deconvolution and diophantine approximation. Ann. Stat. 2004, 32, 1781–1804. [Google Scholar]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: New York, NY, USA, 2009. [Google Scholar]
- Sheng, Y.; Alsdorf, D.E. Automated georeferencing and orthorectification of Amazon basin-wide SAR mosaics using SRTM DEM data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1929–1940. [Google Scholar] [CrossRef]
- Gens, R.; Pottier, E.; Atwood, D.K. Geocoding of polarimetric processing results: Alternative processing strategies. Remote Sens. Lett. 2013, 4, 39–45. [Google Scholar] [CrossRef]
- Cloude, S.R. Polarisation: Applications in Remote Sensing; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Allain, S.; Ferro-Famil, L.; Pottier, E. A polarimetric classification from POLSAR data using SERD/DERD parameters. In Proceedings of the 6th European Conference on Synthetic Aperture Radar, Dresden, Germany, 16–18 May 2006.
- Kim, Y.; van Zyl, J.J. Comparison of forest estimation techniques using SAR data. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1395–1397.
- Birth, G.S.; McVey, G. Measuring the color of growing turf with a reflectance spectroradiometer. Agron. J. 1968, 60, 640–643. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Advancement of Retrogradation (Green Wave Effect) of Natural Vegetation; Texas A & M University: Greenbelt, MD, USA, 1974. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Liu, H.Q.; Huete, A.R. A feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote Sens. 1995, 33, 457–465. [Google Scholar]
- Jin, X.L.; Wang, K.R.; Xiao, C.H.; Diao, W.Y.; Wang, F.Y.; Chen, B.; Li, S.K. Comparison of two methods for estimation of leaf total chlorophyll content using remote sensing in wheat. Field Crop. Res. 2012, 135, 24–29. [Google Scholar] [CrossRef]
- Jin, X.L.; Xu, X.G.; Song, X.Y.; Li, Z.H.; Wang, J.H.; Guo, W.S. Estimation of leaf water content in winter wheat using grey relational analysis–Partial least squares modeling with hyperspectral data. Agron. J. 2013, 105, 1385–1392. [Google Scholar] [CrossRef]
- Wang, B.S. Field-Experiment and Statistic-Method; China Agriculture Press: Beijing, China, 2002. [Google Scholar]
- Koay, J.Y.; Tan, C.P.; Lim, K.S.; Bin Abu Bakar, S.B.; Ewe, H.T.; Chuah, H.T.; Kong, J.A. Paddy fields as electrically dense media: Theoretical modeling and measurement comparisons. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2837–2849. [Google Scholar] [CrossRef]
- Karam, M.; Fung, A.; Lang, R.; Chauhan, N. A microwave scattering model for layered vegetation. IEEE Trans. Geosci. Remote Sens. 1992, 30, 767–784. [Google Scholar] [CrossRef]
- Fourty, T.; Baret, F. Vegetation water and dry matter contents estimated from top-of-the-atmosphere reflectance data: A simulation. Remote Sens. Environ. 1997, 61, 34–45. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, X.; Yang, G.; Xu, X.; Yang, H.; Feng, H.; Li, Z.; Shen, J.; Lan, Y.; Zhao, C. Combined Multi-Temporal Optical and Radar Parameters for Estimating LAI and Biomass in Winter Wheat Using HJ and RADARSAR-2 Data. Remote Sens. 2015, 7, 13251-13272. https://doi.org/10.3390/rs71013251
Jin X, Yang G, Xu X, Yang H, Feng H, Li Z, Shen J, Lan Y, Zhao C. Combined Multi-Temporal Optical and Radar Parameters for Estimating LAI and Biomass in Winter Wheat Using HJ and RADARSAR-2 Data. Remote Sensing. 2015; 7(10):13251-13272. https://doi.org/10.3390/rs71013251
Chicago/Turabian StyleJin, Xiuliang, Guijun Yang, Xingang Xu, Hao Yang, Haikuan Feng, Zhenhai Li, Jiaxiao Shen, Yubin Lan, and Chunjiang Zhao. 2015. "Combined Multi-Temporal Optical and Radar Parameters for Estimating LAI and Biomass in Winter Wheat Using HJ and RADARSAR-2 Data" Remote Sensing 7, no. 10: 13251-13272. https://doi.org/10.3390/rs71013251
APA StyleJin, X., Yang, G., Xu, X., Yang, H., Feng, H., Li, Z., Shen, J., Lan, Y., & Zhao, C. (2015). Combined Multi-Temporal Optical and Radar Parameters for Estimating LAI and Biomass in Winter Wheat Using HJ and RADARSAR-2 Data. Remote Sensing, 7(10), 13251-13272. https://doi.org/10.3390/rs71013251