A New Method to Combine Coastal Sea Surface Height Estimates from Multiple Retrackers by Using the Dijkstra Algorithm
Abstract
:1. Introduction
2. Data and Study Region
2.1. Altimeter Data
2.2. Tide Gauge Records
2.3. Study Region
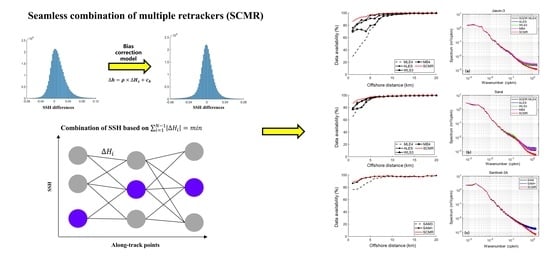
3. Methodology
- (1)
- To optimize the range and geophysical corrections in the study area. The along-track SSH estimates are obtained as follows,where the retracked range is derived from the waveform retracker, which is the input as illustrated in Figure 2.The appropriate range and geophysical corrections are selected based on the trade-off between minimum SLA variance criterion and data availability, which will be described in Section 3.1.
- (2)
- To calculate the temporal-averaged MSS at each along-track point (Section 3.1). The SSH estimates from all repeat cycles are referenced to the Topex ellipsoid and reduced to the nominal points of each reference track by using the nearest neighborhood approach. The reduced SSH estimates are then used to calculate the temporal-averaged MSS at each along-track point following the method in [4]. The along-track MSS can be used to remove the SSH outliers (see Section 3.4).
- (3)
- To determine and remove the bias of SSH estimates from different retrackers. The SSH bias is estimated with respect to the WLS3 (SAMOSA+) retracker for Jason-3 and Saral missions (Sentinel-3A mission) by the method introduced in Section 3.2.
- (4)
- To derive the most appropriate along-track SSH profile using the Dijkstra algorithm. This assumes that the high-rate SSH estimates vary insignificantly along the ground track (see Section 3.3). The along-track SLA profile is finally derived as the difference between the along-track SSH and MSS.
3.1. Regional Corrections and MSS
3.2. Removing SSH Bias
3.3. Combining SSH Estimates by Dijkstra Algorithm
3.4. Assessing the Performance of SCMR Strategy
4. Results
4.1. SSH Bias between Different Retrackers
4.2. Data Availability and Precision
4.3. Validation against Tide Gauge Records
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deng, X.; Featherstone, W.E. A coastal retracking system for satellite radar altimeter waveforms: Application to ERS-2 around Australia. J. Geophys. Res. Ocean. 2006, 111. [Google Scholar] [CrossRef]
- Jain, M. Improved Sea-Level Determination in the Arctic Regions through Development of Tolerant Altimetry Retracking. Ph.D. Thesis, DTU Space, Lyngby, Denmark, 2015. [Google Scholar]
- Idris, N.H.; Deng, X.; Din, A.H.M.; Idris, N.H. CAWRES: A waveform retracking fuzzy expert system for optimizing coastal sea levels from Jason-1 and Jason-2 satellite altimetry data. Remote Sens. 2017, 9, 603. [Google Scholar] [CrossRef]
- Peng, F.; Deng, X.; Cheng, X. Quantifying the precision of retracked Jason-2 sea level data in the 0–5 km Australian coastal zone. Remote Sens. Environ. 2021, 263, 112539. [Google Scholar] [CrossRef]
- Yang, L.; Lin, M.; Liu, Q.; Pan, D. A coastal altimetry retracking strategy based on waveform classification and sub-waveform extraction. Int. J. Remote Sens. 2012, 33, 24. [Google Scholar] [CrossRef]
- Peng, F.; Deng, X. A new retracking technique for Brown peaky altimetric waveforms. Mar. Geod. 2018, 41, 99–125. [Google Scholar] [CrossRef]
- Passaro, M.; Cipollini, P.; Vignudelli, S.; Quartly, G.D.; Snaith, H.M. ALES: A multi-mission adaptive subwaveform retracker for coastal and open ocean altimetry. Remote Sens. Environ. 2014, 145, 173–189. [Google Scholar] [CrossRef]
- Poisson, J.C.; Quartly, G.D.; Kurekin, A.A.; Thibaut, P.; Hoang, D.; Nencioli, F. Development of an Envisat altimetry processor providing sea level continuity between open ocean and Arctic leads. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5299–5319. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Roscher, R.; Uebbing, B.; Kusche, J. STAR: Spatio-temporal altimeter waveform retracking using sparse representation and conditional random fields. Remote Sens. Environ. 2017, 201, 148–164. [Google Scholar] [CrossRef]
- Oettershagen, L.; Uebbing, B.; Charfreitag, J.; Mutzel, P.; Kusche, J. mSTAR: Multicriteria Spatio Temporal Altimetry Retracking. In Proceedings of the EGU General Assembly Conference, Virtual, 19–30 April 2021. [Google Scholar]
- Cipollini, P.; Calafat, F.M.; Jevrejeva, S.; Melet, A.; Prandi, P. Monitoring sea level in the coastal zone with satellite altimetry and tide gauges. In Integrative Study of the Mean Sea Level and Its Components; Springer: Berlin/Heidelberg, Germany, 2017; pp. 35–59. [Google Scholar]
- Bonnefond, P.; Verron, J.; Aublanc, J.; Babu, K.N.; Berge-Nguyen, M.; Cancet, M.; Watson, C. The benefits of the Ka-band as evidenced from the SARAL/AltiKa altimetric mission: Quality assessment and unique characteristics of AltiKa data. Remote Sens. 2018, 10, 83. [Google Scholar] [CrossRef]
- Dinardo, S.; Fenoglio-Marc, L.; Buchhaupt, C.; Becker, M.; Scharroo, R.; Fernandes, M.J.; Benveniste, J. Coastal SAR and PLRM altimetry in German Bight and west Baltic Sea. Adv. Space Res. 2018, 62, 1371–1404. [Google Scholar] [CrossRef]
- Fenoglio-Marc, L.; Dinardo, S.; Scharroo, R.; Roland, A.; Sikiric, M.D.; Lucas, B.; Becker, M.; Benveniste, J.; Weiss, R. The German Bight: A validation of CryoSat-2 altimeter data in SAR mode. Adv. Space Res. 2015, 55, 2641–2656. [Google Scholar] [CrossRef]
- Passaro, M.; Rose, S.K.; Andersen, O.B.; Boergens, E.; Calafat, F.M.; Dettmering, D.; Benveniste, J. ALES+: Adapting a homogenous ocean retracker for satellite altimetry to sea ice leads, coastal and inland waters. Remote Sens. Environ. 2018, 211, 456–471. [Google Scholar] [CrossRef]
- Vincent, P.; Steunou, N.; Caubetq, E.; Phalippou, L.; Rey, L.; Thouvenot, E.; Verron, J. AltiKa: A Ka-band altimetry payload and system for operational altimetry during the GMES period. Sensors 2006, 6, 208–234. [Google Scholar] [CrossRef]
- Hithin, N.K.; Remya, P.G.; Nair, T.B.; Harikumar, R.; Kumar, R.; Nayak, S. Validation and intercomparison of SARAL/AltiKa and PISTACH-derived coastal wave heights using in-situ measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2015, 8, 4120–4129. [Google Scholar] [CrossRef]
- Peng, F.; Deng, X. Improving precision of high-rate altimeter sea level anomalies by removing the sea state bias and intra-1-Hz covariant error. Remote Sens. Environ. 2020, 251, 112081. [Google Scholar] [CrossRef]
- Deng, X.; Griffin, D.A.; Ridgway, K.; Church, J.A.; Featherstone, W.E.; White, N.J.; Cahill, M. Satellite altimetry for geodetic, oceanographic, and climate studies in the Australian region. In Coastal Altimetry; Springer: Berlin/Heidelberg, Germany, 2011; pp. 473–508. [Google Scholar]
- Riddell, A.R.; King, M.A.; Watson, C.S. Present-day vertical land motion of Australia from GPS observations and geophysical models. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018034. [Google Scholar] [CrossRef]
- Hemer, M.A.; Church, J.A.; Hunter, J.R. Waves and climate change on the Australian coast. J. Coast. Res. 2007, 50, 432–437. [Google Scholar]
- Nerem, R.S.; Beckley, B.D.; Fasullo, J.T.; Hamlington, B.D.; Masters, D.; Mitchum, G.T. Climate-change–driven accelerated sea-level rise detected in the altimeter era. Proc. Natl. Acad. Sci. USA 2018, 115, 2022–2025. [Google Scholar] [CrossRef]
- Dinardo, S. Techniques and Applications for Satellite SAR Altimetry over Water, Land and Ice. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2020. [Google Scholar]
- Pujol, M.I.; Schaeffer, P.; Faugere, Y.; Raynal, M.; Dibarboure, G.; Picot, N. Gauging the improvement of recent mean sea surface models: A new approach for identifying and quantifying their errors. J. Geophys. Res. Ocean. 2018, 123, 5889–5911. [Google Scholar] [CrossRef]
- Gómez-Enri, J.; Gonzalez, C.J.; Passaro, M.; Vignudelli, S.; Alvarez, O.; Cipollini, P.; Lzquiedo, A. Wind-induced cross-strait sea level variability in the strait of Gibraltar from coastal altimetry and in-situ measurements. Remote Sens. Environ. 2019, 221, 596–608. [Google Scholar] [CrossRef]
- Fernandes, M.J.; Lázaro, C. GPD+ wet tropospheric corrections for CryoSat-2 and GFO altimetry missions. Remote Sens. 2016, 8, 851. [Google Scholar] [CrossRef]
- Cartwright, D.E.; Tayler, R.J. New computations of the tide-generating potential. Geophys. J. Int. 1971, 23, 45–73. [Google Scholar] [CrossRef]
- Cartwright, D.E.; Edden, A.C. Corrected tables of tidal harmonics. Geophys. J. Int. 1973, 33, 253–264. [Google Scholar] [CrossRef]
- Desai, S.; Wahr, J.; Beckley, B. Revisiting the pole tide for and from satellite altimetry. J. Geod. 2015, 89, 1233–1243. [Google Scholar] [CrossRef]
- Gommenginger, C.; Thibaut, P.; Fenoglio-Marc, L.; Quartly, G.; Deng, X.; Gómez-Enri, J.; Challenor, P.; Gao, Y. Retracking altimeter waveforms near the coasts. In Coastal Altimetry; Springer: Berlin, Germany, 2011; pp. 61–101. [Google Scholar]
- Hamlington, B.D.; Gardner, A.S.; Ivins, E.; Lenaerts, J.T.; Reager, J.T.; Trossman, D.S.; Willis, M.J. Understanding of contemporary regional sea-level change and the implications for the future. Rev. Geophys. 2020, 58, e2019RG000672. [Google Scholar] [CrossRef] [PubMed]
- Amarouche, L.; Thibaut, P.; Zanife, O.Z.; Dumount, J.P.; Vincent, P.; Steunou, N. Improving the Jason-1 ground retracking to better account for attitude effects. Mar. Geod. 2004, 27, 171–197. [Google Scholar] [CrossRef]
- Vignudelli, S.; Birol, F.; Benveniste, J.; Fu, L.L.; Picot, N.; Raynal, M.; Roinard, H. Satellite altimetry measurements of sea level in the coastal zone. Surv. Geophys. 2019, 40, 1319–1349. [Google Scholar] [CrossRef]
- Cazenave, A.; Gouzenes, Y.; Birol, F.; Leger, F.; Passaro, M.; Calafat, F.M.; Shaw, A.; Nino, F.; Legeais, J.F.; Oelsmann, J.; et al. Sea level along the world’s coastlines can be measured by a network of virtual altimetry stations. Commun. Earth Environ. 2022, 3, 1–9. [Google Scholar] [CrossRef]
- Zanifé, O.Z.; Vincent, P.; Amarouche, L.; Dumont, J.P.; Thibaut, P.; Labroue, S. Comparison of the Ku-Band range noise level and the relative sea-state bias of the Jason-1, TOPEX, and Poseidon-1 radar altimeters. Mar. Geod. 2003, 26, 201–238. [Google Scholar] [CrossRef]
- Jiang, M.; Xu, K.; Wang, J. Evaluation of Sentinel-6 altimetry data over ocean. Remote Sens. 2023, 15, 12. [Google Scholar] [CrossRef]
- Aldarias, A.; Gómez-Enri, J.; Laiz, I.; Tejedor, B.; Vignudelli, S.; Cipollini, P. Validation of Sentinel-3A SRAL Coastal Sea Level Data at High Posting Rate: 80-Hz. IEEE Transact. Geosci. Remote Sens. 2020, 58, 3809–3821. [Google Scholar] [CrossRef]
- Birol, F.; Léger, F.; Gouzenes, Y.; Schwatke, C.; Benveniste, J. The X-TRACK/ALES multi-mission processing system: New advances in altimetry towards the coast. Adv. Space Res. 2021, 67, 2398–2415. [Google Scholar] [CrossRef]
- Schlembach, F.; Passaro, M.; Quartly, G.D.; Kurekin, A.; Nencioli, F.; Dodet, G.; Piollé, J.-F.; Ardhuin, F.; Bidlot, J.; Schwatke, C.; et al. Round Robin Assessment of Radar Altimeter Low Resolution Mode and Delay-Doppler Retracking Algorithms for Significant Wave Height. Remote Sens. 2020, 12, 1254. [Google Scholar] [CrossRef]















| Missions | Jason-3 | Saral | Sentinel-3A | |
|---|---|---|---|---|
| Corrections | ||||
| DTC | ECMWF | ERA | ECMWF | |
| WTC | GPD+ [27] | ECMWF | ||
| Ionospheric correction | GIM | |||
| Sea state bias | Peng and Deng [19] | |||
| Geocentric ocean tide | FES2014 | |||
| DAC | MOG2D | |||
| Solid earth tide | Cartwright and Taylor [28] Cartwright and Taylor [29] | |||
| Pole tide | Desai et al. [30] | |||
| Mean sea surface | Along-track MSS [4] | |||
| Missions | Jason-3 | Saral | Sentinel-3A | ||||
|---|---|---|---|---|---|---|---|
| Retrackers | |||||||
| SGDR MLE4 | −0.0558 | 16.9 | −0.0778 | 3.7 | / | / | |
| ALES | −0.0676 | −17.1 | −0.0722 | −9.6 | / | / | |
| MB4 | −0.0866 | −2.2 | −0.0993 | −7.3 | / | / | |
| SAM | / | / | / | / | 0.0136 | 5.3 | |
| Missions | Jason-3 | Saral | Sentinel-3A | ||||
|---|---|---|---|---|---|---|---|
| Retrackers | Before | After | Before | After | Before | After | |
| SGDR MLE4 | 22.9 | 0.6 | 6.0 | 0.2 | / | / | |
| ALES | −18.6 | −2.6 | −6.4 | −0.4 | / | / | |
| MB4 | −7.0 | −3.0 | −7.8 | −0.8 | / | / | |
| SAM | / | / | / | / | 6.8 | 0.5 | |
| Missions | Jason-3 | Saral | Sentinel-3A | ||||
|---|---|---|---|---|---|---|---|
| Retrackers | Before | After | Before | After | Before | After | |
| SGDR MLE4 | 57.4 | 28.7 | 45.9 | 42.7 | / | / | |
| ALES | 43.2 | 35.5 | 37.4 | 33.6 | / | / | |
| MB4 | 36.2 | 30.5 | 36.2 | 32.3 | / | / | |
| SAM | / | / | / | / | 63.0 | 62.5 | |
| Missions | Jason-3 | Saral | Sentinel-3A | ||||
|---|---|---|---|---|---|---|---|
| Retrackers | 0–20 km | 20–100 km | 0–20 km | 20–100 km | 0–20 km | 20–100 km | |
| SCMR vs. MLE4 | 13.90 | 10.48 | 15.60 | 14.07 | / | / | |
| SCMR vs. ALES | 24.32 | 14.67 | 20.67 | 14.26 | / | / | |
| SCMR vs. WLS3 | 16.54 | 10.24 | 11.74 | 8.35 | / | / | |
| SCMR vs. MB4 | 21.97 | 12.69 | 17.54 | 12.03 | / | / | |
| SCMR vs. SAM | / | / | / | / | 25.07 | 25.07 | |
| SCMR vs. SAM+ | / | / | / | / | 21.18 | 19.68 | |
| Missions | Jason-3 | Saral | Sentinel-3A | |
|---|---|---|---|---|
| Retrackers | ||||
| SGDR MLE4 | 6.18 | 4.41 | / | |
| ALES | 6.61 | 4.97 | / | |
| WLS3 | 6.34 | 4.70 | / | |
| MB4 | 6.71 | 4.57 | / | |
| SAM | / | / | 5.32 | |
| SAM+ | / | / | 5.04 | |
| SCMR | 4.65 | 3.05 | 3.42 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, F.; Deng, X.; Jiang, M.; Dinardo, S.; Shen, Y. A New Method to Combine Coastal Sea Surface Height Estimates from Multiple Retrackers by Using the Dijkstra Algorithm. Remote Sens. 2023, 15, 2329. https://doi.org/10.3390/rs15092329
Peng F, Deng X, Jiang M, Dinardo S, Shen Y. A New Method to Combine Coastal Sea Surface Height Estimates from Multiple Retrackers by Using the Dijkstra Algorithm. Remote Sensing. 2023; 15(9):2329. https://doi.org/10.3390/rs15092329
Chicago/Turabian StylePeng, Fukai, Xiaoli Deng, Maofei Jiang, Salvatore Dinardo, and Yunzhong Shen. 2023. "A New Method to Combine Coastal Sea Surface Height Estimates from Multiple Retrackers by Using the Dijkstra Algorithm" Remote Sensing 15, no. 9: 2329. https://doi.org/10.3390/rs15092329
APA StylePeng, F., Deng, X., Jiang, M., Dinardo, S., & Shen, Y. (2023). A New Method to Combine Coastal Sea Surface Height Estimates from Multiple Retrackers by Using the Dijkstra Algorithm. Remote Sensing, 15(9), 2329. https://doi.org/10.3390/rs15092329