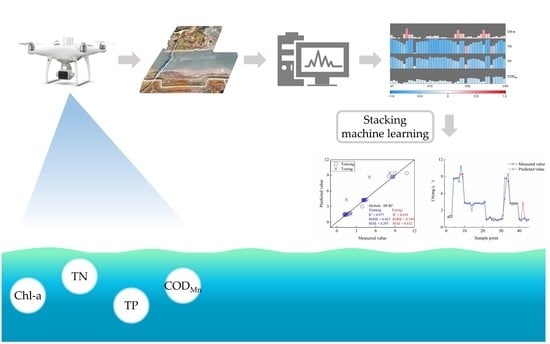
UAV Multispectral Image-Based Urban River Water Quality Monitoring Using Stacked Ensemble Machine Learning Algorithms—A Case Study of the Zhanghe River, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection and Processing
2.2.1. UAV Multispectral Image Collection and Preprocessing
2.2.2. Ground Monitoring Data
2.3. Method
2.3.1. Calculation of Spectral Index
2.3.2. Traditional Regression Methods
2.3.3. Stacking ML Method
2.3.4. Accuracy Evaluation
3. Results
3.1. Data Analysis
3.2. Spectral Index Correlation Analysis
3.3. Results of Simple Regression Methods
3.4. Comparison of Results of ML Models and Stacked ML Models
4. Discussion
4.1. Performance of Stacked ML Models in Monitoring Water Quality
4.2. Differences in Inversion Models for Different Water Quality Parameters
4.3. Limitations and Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fezzi, C.; Harwood, A.R.; Lovett, A.A.; Bateman, I.J. The environmental impact of climate change adaptation on land use and water quality. Nat. Clim. Chang. 2015, 5, 255–260. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Cao, Y.; Fan, Y.; Yang, H.; Feng, X.; Li, L.; Zhang, H.; Xing, L.; Zhao, M. Ladderane records over the last century in the East China sea: Proxies for anammox and eutrophication changes. Water Res. 2019, 156, 297–304. [Google Scholar] [CrossRef] [PubMed]
- Basu, N.B.; Van Meter, K.J.; Byrnes, D.K.; Van Cappellen, P.; Brouwer, R.; Jacobsen, B.H.; Jarsjo, J.; Rudolph, D.L.; Cunha, M.C.; Nelson, N.; et al. Managing nitrogen legacies to accelerate water quality improvement. Nat. Geosci. 2022, 15, 97–105. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, L.; Mu, C.; Huang, X. Water quality change and pollution source accounting of Licun River under long-term governance. Sci. Rep. 2022, 12, 2779. [Google Scholar] [CrossRef] [PubMed]
- Tao, T.; Xin, K. A sustainable plan for China’s drinking water. Nature 2014, 511, 527–528. [Google Scholar] [CrossRef] [PubMed]
- Determan, R.T.; White, J.D.; McKenna, L.W., III. Quantile regression illuminates the successes and shortcomings of long-term eutrophication remediation efforts in an urban river system. Water Res. 2021, 202, 117434. [Google Scholar] [CrossRef] [PubMed]
- Guan, Q.; Feng, L.; Hou, X.; Schurgers, G.; Zheng, Y.; Tang, J. Eutrophication changes in fifty large lakes on the Yangtze Plain of China derived from MERIS and OLCI observations. Remote Sens. Environ. 2020, 246, 111890. [Google Scholar] [CrossRef]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef] [Green Version]
- Feng, L.; Dai, Y.; Hou, X.; Xu, Y.; Liu, J.; Zheng, C. Concerns about phytoplankton bloom trends in global lakes. Nature 2021, 590, E35–E47. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, L.; Zhou, Y.; Zhang, L.; Yao, X.; Shi, K.; Jeppesen, E.; Yu, Q.; Zhu, W. Chromophoric dissolved organic matter in inland waters: Present knowledge and future challenges. Sci. Total Environ. 2021, 759, 143550. [Google Scholar] [CrossRef]
- Doernhoefer, K.; Oppelt, N. Remote sensing for lake research and monitoring—Recent advances. Ecol. Indic. 2016, 64, 105–122. [Google Scholar] [CrossRef]
- Aurin, D.; Mannino, A.; Franz, B. Spatially resolving ocean color and sediment dispersion in river plumes, coastal systems, and continental shelf waters. Remote Sens. Environ. 2013, 137, 212–225. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Shen, Q.; Yao, Y.; Li, J.; Chen, F.; Wang, R.; Xu, W.; Gao, Z.; Wang, L.; Zhou, Y. Estimation of Chlorophyll-a Concentrations in Small Water Bodies: Comparison of Fused Gaofen-6 and Sentinel-2 Sensors. Remote Sens. 2022, 14, 229. [Google Scholar] [CrossRef]
- Sagan, V.; Peterson, K.T.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, B.A.; Maalouf, S.; Adams, C. Monitoring inland water quality using remote sensing: Potential and limitations of spectral indices, bio-optical simulations, machine learning, and cloud computing. Earth-Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Templin, T.; Popielarczyk, D.; Kosecki, R. Application of Low-Cost Fixed-Wing UAV for Inland Lakes Shoreline Investigation. Pure Appl. Geophys. 2018, 175, 3263–3283. [Google Scholar] [CrossRef] [Green Version]
- Acharya, B.S.; Bhandari, M.; Bandini, F.; Pizarro, A.; Perks, M.; Joshi, D.R.; Wang, S.; Dogwiler, T.; Ray, R.L.; Kharel, G.; et al. Unmanned Aerial Vehicles in Hydrology and Water Management: Applications, Challenges, and Perspectives. Water Resour. Res. 2021, 57, e2021WR029925. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, S.; Fu, Y.H.; Xiao, Y.; Wu, W.; Wang, H.; de Beurs, K. Comparison of Multi-Methods for Identifying Maize Phenology Using PhenoCams. Remote Sens. 2022, 14, 244. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, Y.; Shi, K.; Zhang, Y.; Li, N.; Wang, W.; Huang, X.; Qin, B. Monitoring water quality using proximal remote sensing technology. Sci. Total Environ. 2022, 803, 149805. [Google Scholar] [CrossRef]
- Xiang, T.-Z.; Xia, G.-S.; Zhang, L. Mini-Unmanned Aerial Vehicle-Based Remote Sensing Techniques, applications, and prospects. IEEE Geosci. Remote Sens. Mag. 2019, 7, 29–63. [Google Scholar] [CrossRef] [Green Version]
- Yao, H.; Qin, R.; Chen, X. Unmanned Aerial Vehicle for Remote Sensing Applications-A Review. Remote Sens. 2019, 11, 1443. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Fu, Y.H.; Chen, S.; Bryant, C.R.; Li, X.; Senthilnath, J.; Sun, H.; Wang, S.; Wu, Z.; de Beurs, K. Integrating spectral and textural information for identifying the tasseling date of summer maize using UAV based RGB images. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102435. [Google Scholar] [CrossRef]
- Chen, B.; Mu, X.; Chen, P.; Wang, B.; Choi, J.; Park, H.; Xu, S.; Wu, Y.; Yang, H. Machine learning-based inversion of water quality parameters in typical reach of the urban river by UAV multispectral data. Ecol. Indic. 2021, 133, 108434. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L.; Ren, H.; Liu, Y.; Zheng, Y.; Liu, Y.; Dong, J. Mapping Water Quality Parameters in Urban Rivers from Hyperspectral Images Using a New Self-Adapting Selection of Multiple Artificial Neural Networks. Remote Sens. 2020, 12, 336. [Google Scholar] [CrossRef] [Green Version]
- Niu, C.; Tan, K.; Jia, X.; Wang, X. Deep learning based regression for optically inactive inland water quality parameter estimation using airborne hyperspectral imagery*. Environ. Pollut. 2021, 286, 117534. [Google Scholar] [CrossRef]
- Su, T.-C. A study of a matching pixel by pixel (MPP) algorithm to establish an empirical model of water quality mapping, as based on unmanned aerial vehicle (UAV) images. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 213–224. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L.; Ren, H.; Deng, L.; Zhang, P. Retrieval of Water Quality Parameters from Hyperspectral Images Using Hybrid Bayesian Probabilistic Neural Network. Remote Sens. 2020, 12, 1567. [Google Scholar] [CrossRef]
- Sibanda, M.; Mutanga, O.; Chimonyo, V.G.P.; Clulow, A.D.; Shoko, C.; Mazvimavi, D.; Dube, T.; Mabhaudhi, T. Application of Drone Technologies in Surface Water Resources Monitoring and Assessment: A Systematic Review of Progress, Challenges, and Opportunities in the Global South. Drones 2021, 5, 84. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Nguyen, H.; et al. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Guo, Y.; Fu, Y.; Hao, F.; Zhang, X.; Wu, W.; Jin, X.; Bryant, C.R.; Senthilnath, J. Integrated phenology and climate in rice yields prediction using machine learning methods. Ecol. Indic. 2021, 120, 106935. [Google Scholar] [CrossRef]
- Arias-Rodriguez, L.F.; Duan, Z.; de Jesus Diaz-Torres, J.; Hazas, M.B.; Huang, J.; Kumar, B.U.; Tuo, Y.; Disse, M. Integration of Remote Sensing and Mexican Water Quality Monitoring System Using an Extreme Learning Machine. Sensors 2021, 21, 4118. [Google Scholar] [CrossRef]
- Ma, Y.; Song, K.; Wen, Z.; Liu, G.; Shang, Y.; Lyu, L.; Du, J.; Yang, Q.; Li, S.; Tao, H.; et al. Remote Sensing of Turbidity for Lakes in Northeast China Using Sentinel-2 Images with Machine Learning Algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9132–9146. [Google Scholar] [CrossRef]
- Wei, L.; Huang, C.; Zhong, Y.; Wang, Z.; Hu, X.; Lin, L. Inland Waters Suspended Solids Concentration Retrieval Based on PSO-LSSVM for UAV-Borne Hyperspectral Remote Sensing Imagery. Remote Sens. 2019, 11, 1455. [Google Scholar] [CrossRef] [Green Version]
- Wei, L.; Wang, Z.; Huang, C.; Zhang, Y.; Wang, Z.; Xia, H.; Cao, L. Transparency Estimation of Narrow Rivers by UAV-Borne Hyperspectral Remote Sensing Imagery. IEEE Access 2020, 8, 168137–168153. [Google Scholar] [CrossRef]
- Liu, J.; Ding, J.; Ge, X.; Wang, J. Evaluation of Total Nitrogen in Water via Airborne Hyperspectral Data: Potential of Fractional Order Discretization Algorithm and Discrete Wavelet Transform Analysis. Remote Sens. 2021, 13, 4643. [Google Scholar] [CrossRef]
- Qun’ou, J.; Lidan, X.; Siyang, S.; Meilin, W.; Huijie, X. Retrieval model for total nitrogen concentration based on UAV hyper spectral remote sensing data and machine learning algorithms—A case study in the Miyun Reservoir, China. Ecol. Indic. 2021, 124, 107356. [Google Scholar] [CrossRef]
- Feng, X.; Liang, Y.; Shi, X.; Xu, D.; Wang, X.; Guan, R. Overfitting Reduction of Text Classification Based on AdaBELM. Entropy 2017, 19, 330. [Google Scholar] [CrossRef] [Green Version]
- Dietterich, T. Overfitting and undercomputing in machine learning. ACM Comput. Surv. 1995, 27, 326–327. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble methods in machine learning. In Multiple Classifier Systems; Kittler, J., Roli, F., Eds.; Lecture Notes in Computer Science; Springer: Boston, MA, USA, 2000; Volume 1857, pp. 1–15. [Google Scholar]
- Breiman, L. Stacked regressions. Machine Learning 1996, 24, 49–64. [Google Scholar] [CrossRef] [Green Version]
- Pavlyshenko, B. Using Stacking Approaches for Machine Learning Models. In Proceedings of the 2nd IEEE International Conference on Data Stream Mining and Processing (DSMP), Lviv, Ukraine, 21–25 August 2018; pp. 255–258. [Google Scholar]
- Floehr, T.; Xiao, H.; Scholz-Starke, B.; Wu, L.; Hou, J.; Yin, D.; Zhang, X.; Ji, R.; Yuan, X.; Ottermanns, R.; et al. Solution by dilution?—A review on the pollution status of the Yangtze River. Environ. Sci. Pollut. Res. 2013, 20, 6934–6971. [Google Scholar] [CrossRef]
- Tian, J.; Chang, J.; Zhang, Z.; Wang, Y.; Wu, Y.; Jiang, T. Influence of Three Gorges Dam on Downstream Low Flow. Water 2019, 11, 65. [Google Scholar] [CrossRef] [Green Version]
- Zeng, C.; Richardson, M.; King, D.J. The impacts of environmental variables on water reflectance measured using a lightweight unmanned aerial vehicle (UAV)-based spectrometer system. ISPRS J. Photogramm. Remote Sens. 2017, 130, 217–230. [Google Scholar] [CrossRef]
- Giles, A.B.; Davies, J.E.; Ren, K.; Kelaher, B. A deep learning algorithm to detect and classify sun glint from high-resolution aerial imagery over shallow marine environments. ISPRS J. Photogramm. Remote Sens. 2021, 181, 20–26. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Wu, Z.; Wang, S.; Sun, H.; Senthilnath, J.; Wang, J.; Bryant, C.R.; Fu, Y. Modified Red Blue Vegetation Index for Chlorophyll Estimation and Yield Prediction of Maize from Visible Images Captured by UAV. Sensors 2020, 20, 5055. [Google Scholar] [CrossRef]
- Ha, N.T.T.; Koike, K.; Nhuan, M.T. Improved Accuracy of Chlorophyll-a Concentration Estimates from MODIS Imagery Using a Two-Band Ratio Algorithm and Geostatistics: As Applied to the Monitoring of Eutrophication Processes over Tien Yen Bay (Northern Vietnam). Remote Sens. 2014, 6, 421–442. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Wang, S.; Yang, R.; Ma, Y.; Shen, M.; You, Y.; Hai, K.; Baqa, M.F. Remote Sensing Retrieval of Turbidity in Alpine Rivers based on high Spatial Resolution Satellites. Remote Sens. 2019, 11, 3010. [Google Scholar] [CrossRef] [Green Version]
- Bouasria, A.; Namr, K.I.; Rahimi, A.; Ettachfini, E.M.; Rerhou, B. Evaluation of Landsat 8 image pansharpening in estimating soil organic matter using multiple linear regression and artificial neural networks. Geo-Spat. Inf. Sci. 2022. [Google Scholar] [CrossRef]
- Forkuor, G.; Hounkpatin, O.K.L.; Welp, G.; Thiel, M. High Resolution Mapping of Soil Properties Using Remote Sensing Variables in South-Western Burkina Faso: A Comparison of Machine Learning and Multiple Linear Regression Models. PLoS ONE 2017, 12, e0170478. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. Ser. B-Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Han, H.; Wan, R.; Li, B. Estimating Forest Aboveground Biomass Using Gaofen-1 Images, Sentinel-1 Images, and Machine Learning Algorithms: A Case Study of the Dabie Mountain Region, China. Remote Sens. 2022, 14, 176. [Google Scholar] [CrossRef]
- Said, S.; Khan, S.A. Remote sensing-based water quality index estimation using data-driven approaches: A case study of the Kali River in Uttar Pradesh, India. Environ. Dev. Sustain. 2021, 23, 18252–18277. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Sheykhmousa, M.; Mahdianpari, M.; Ghanbari, H.; Mohammadimanesh, F.; Ghamisi, P.; Homayouni, S. Support Vector Machine Versus Random Forest for Remote Sensing Image Classification: A Meta-Analysis and Systematic Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6308–6325. [Google Scholar] [CrossRef]
- Belgiu, M.; Dragut, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C.; Assoc Comp, M. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Xu, Y.; Zhen, J.; Jiang, X.; Wang, J. Mangrove species classification with UAV-based remote sensing data and XGBoost. J. Remote Sens. 2021, 25, 737–752. [Google Scholar]
- Shen, H.; Shi, J.; Xu, J.; Zhu, S.; Zheng, J. Wave forecasting algorithm with stacking ensemble machine learning method. J. Hohai Univ. Nat. Sci. 2020, 48, 354–358. [Google Scholar]
- Meharie, M.G.; Mengesha, W.J.; Gariy, Z.A.; Mutuku, R.N.N. Application of stacking ensemble machine learning algorithm in predicting the cost of highway construction projects. Eng. Constr. Archit. Manag. 2021; online ahead of print. [Google Scholar] [CrossRef]
- Cillero Castro, C.; Dominguez Gomez, J.A.; Delgado Martin, J.; Hinojo Sanchez, B.A.; Cereijo Arango, J.L.; Cheda Tuya, F.A.; Diaz-Varela, R. An UAV and Satellite Multispectral Data Approach to Monitor Water Quality in Small Reservoirs. Remote Sens. 2020, 12, 1514. [Google Scholar] [CrossRef]
- Kupssinsku, L.S.; Guimaraes, T.T.; de Souza, E.M.; Zanotta, D.C.; Veronez, M.R.; Gonzaga, L., Jr.; Mauad, F.F. A Method for Chlorophyll-a and Suspended Solids Prediction through Remote Sensing and Machine Learning. Sensors 2020, 20, 2125. [Google Scholar] [CrossRef] [Green Version]
- Bo, Z.; Bai, Z.; Mei, H.; Hongtao, D.; Kaishan, S.; Zongming, W. Advance in remote sensing of lake water quality. Adv. Water Sci. 2007, 18, 301–310. [Google Scholar]
- Wang, E.K.; Wang, F.; Sun, R.P.; Liu, X. A new privacy attack network for remote sensing images classification with small training samples. Math. Biosci. Eng. 2019, 16, 4456–4476. [Google Scholar] [CrossRef] [PubMed]
- Rocha, A.D.; Groen, T.A.; Skidmore, A.K.; Darvishzadeh, R.; Willemen, L. The Naive Overfitting Index Selection (NOIS): A new method to optimize model complexity for hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2017, 133, 61–74. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Alikas, K.; Anstee, J.; Barbosa, C.; Binding, C.; Bresciani, M.; Cremella, B.; Giardino, C.; Gurlin, D.; et al. Simultaneous retrieval of selected optical water quality indicators from Landsat-8, Sentinel-2, and Sentinel-3. Remote Sens. Environ. 2022, 270, 112860. [Google Scholar] [CrossRef]
- Mathew, M.M.; Rao, N.S.; Mandla, V.R. Development of regression equation to study the Total Nitrogen, Total Phosphorus and Suspended Sediment using remote sensing data in Gujarat and Maharashtra coast of India. J. Coast. Conserv. 2017, 21, 917–927. [Google Scholar] [CrossRef]
- Xiong, Y.; Ran, Y.; Zhao, S.; Zhao, H.; Tian, Q. Remotely assessing and monitoring coastal and inland water quality in China: Progress, challenges and outlook. Crit. Rev. Environ. Sci. Technol. 2020, 50, 1266–1302. [Google Scholar] [CrossRef]
- Ariman, S. Determination of inactive water quality variables by MODIS data: A case study in the Kizilirmak Delta-Balik Lake, Turkey. Estuar. Coast. Shelf Sci. 2021, 260, 107505. [Google Scholar] [CrossRef]
- Vakili, T.; Amanollahi, J. Determination of optically inactive water quality variables using Landsat 8 data: A case study in Geshlagh reservoir affected by agricultural land use. J. Clean. Prod. 2020, 247, 119134. [Google Scholar] [CrossRef]
- Guo, H.; Huang, J.J.; Chen, B.; Guo, X.; Singh, V.P. A machine learning-based strategy for estimating non-optically active water quality parameters using Sentinel-2 imagery. Int. J. Remote Sens. 2021, 42, 1841–1866. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, H.; Bi, S.; Lyu, H. Research progress of remote sensing monitoring of case II water environmental parameters based on water optical classification. J. Remote Sens. 2022, 26, 19–31. [Google Scholar]
- Guo, Y.; Senthilnath, J.; Wu, W.; Zhang, X.; Zeng, Z.; Huang, H. Radiometric Calibration for Multispectral Camera of Different Imaging Conditions Mounted on a UAV Platform. Sustainability 2019, 11, 978. [Google Scholar] [CrossRef] [Green Version]
- Lee, Z.P.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Tian, G.; Wang, X.; Wang, X.; Song, Q. The Methods of Water Spectra Measurement and Analysis I: Above-Water Method. J. Remote Sens. 2004, 8, 37–44. [Google Scholar]
- Chen, Y.; Shen, F. Influence of Suspended Particulate Matter on Chlorophyll-a Retrieval Algorithms in Yangtze River Estuary and Adjacent Turbid Waters. Remote Sens. Technol. Appl. 2016, 31, 126–133. [Google Scholar]
- Zhang, Y.; Wu, L.; Deng, L.; Ouyang, B. Retrieval of water quality parameters from hyperspectral images using a hybrid feedback deep factorization machine model. Water Res. 2021, 204, 117618. [Google Scholar] [CrossRef] [PubMed]








| Band | Wavelength Range (nm) |
|---|---|
| Blue | 450 ± 16 |
| Green | 560 ± 16 |
| Red | 650 ± 16 |
| Red Edge | 730 ± 16 |
| NIR | 840 ± 26 |
| Latitude (°) | Longitude (°) | Height (m) | |
|---|---|---|---|
| GCP1 | 31.259 **** 206 | 118.348 **** 842 | 14.486 |
| GCP2 | 31.261 **** 197 | 118.346 **** 353 | 14.664 |
| GCP3 | 31.263 **** 819 | 118.344 **** 467 | 14.742 |
| GCP4 | 31.265 **** 372 | 118.342 **** 444 | 15.035 |
| GCP5 | 31.266 **** 428 | 118.339 **** 442 | 14.724 |
| GCP6 | 31.194 **** 003 | 118.335 **** 058 | 13.205 |
| GCP7 | 31.193 **** 181 | 118.339 **** 867 | 15.005 |
| GCP8 | 31.170 **** 525 | 118.373 **** 894 | 15.123 |
| GCP9 | 31.166 **** 014 | 118.373 **** 214 | 14.861 |
| GCP10 | 31.161 **** 006 | 118.372 **** 244 | 14.867 |
| GCP11 | 31.160 **** 542 | 118.372 **** 544 | 14.660 |
| GCP12 | 31.161 **** 264 | 118.369 **** 700 | 14.486 |
| GCP13 | 31.164 **** 594 | 118.368 **** 031 | 14.672 |
| GCP14 | 31.170 **** 653 | 118.368 **** 997 | 14.761 |
| GCP15 | 31.189 **** 236 | 118.334 **** 994 | 14.022 |
| GCP16 | 31.190 **** 422 | 118.330 **** 050 | 13.859 |
| GCP17 | 31.258 **** 436 | 118.345 **** 289 | 14.597 |
| GCP18 | 31.260 **** 203 | 118.343 **** 697 | 14.292 |
| GCP19 | 31.262 **** 744 | 118.339 **** 114 | 14.376 |
| GCP20 | 31.263 **** 244 | 118.336 **** 519 | 14.350 |
| GCP21 | 31.265 **** 744 | 118.334 **** 228 | 14.695 |
| Index | Formula | Index | Formula | Index | Formula |
|---|---|---|---|---|---|
| V1 | B1 | V16 | B1 + B2 | V31 | B2/B4 |
| V2 | B2 | V17 | B1 + B3 | V32 | B2/B5 |
| V3 | B3 | V18 | B1 + B4 | V33 | B3/B4 |
| V4 | B4 | V19 | B1 + B5 | V34 | B3/B5 |
| V5 | B5 | V20 | B2 + B3 | V35 | B4/B5 |
| V6 | B1 − B2 | V21 | B2 + B4 | V36 | (B1 − B2)/(B1 + B2) |
| V7 | B1 − B3 | V22 | B2 + B5 | V37 | (B1 − B3)/(B1 + B3) |
| V8 | B1 − B4 | V23 | B3 + B4 | V38 | (B1 − B4)/(B1 + B4) |
| V9 | B1 − B5 | V24 | B3 + B5 | V39 | (B1 − B5)/(B1 + B5) |
| V10 | B2 − B3 | V25 | B4 + B5 | V40 | (B2 − B3)/(B2 + B3) |
| V11 | B2 − B4 | V26 | B1/B2 | V41 | (B2 − B4)/(B2 + B4) |
| V12 | B2 − B5 | V27 | B1/B3 | V42 | (B2 − B5)/(B2 + B5) |
| V13 | B3 − B4 | V28 | B1/B4 | V43 | (B3 − B4)/(B3 + B4) |
| V14 | B3 − B5 | V29 | B1/B5 | V44 | (B3 − B5)/(B3 + B5) |
| V15 | B4 − B5 | V30 | B2/B3 | V45 | (B4 − B5)/(B4 + B5) |
| Date | Chl-a (μg/L) | TN (mg/L) | TP (mg/L) | CODMn (mg/L) | |
|---|---|---|---|---|---|
| Zhanghe River 20 February 2021 (N = 13) | Max | 74.00 | 10.80 | 0.38 | 6.10 |
| Min | 6.00 | 1.90 | 0.09 | 3.10 | |
| Mean | 33.62 | 6.45 | 0.23 | 4.36 | |
| SD | 25.60 | 3.29 | 0.10 | 1.01 | |
| Zhanghe River 9–10 December 2021 (N = 32) | Max | 13.50 | 4.58 | 0.17 | 4.90 |
| Min | 1.00 | 1.12 | 0.06 | 2.80 | |
| Mean | 4.81 | 2.88 | 0.11 | 3.96 | |
| SD | 2.76 | 1.45 | 0.03 | 0.52 | |
| All data (N = 45) | Max | 74.00 | 10.80 | 0.38 | 6.10 |
| Min | 1.00 | 1.12 | 0.06 | 2.80 | |
| Mean | 12.88 | 3.94 | 0.15 | 4.06 | |
| SD | 18.94 | 2.64 | 0.08 | 0.71 |
| Parameter | Index | Method | Training Dataset | Testing Dataset | ||
|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | |||
| Chl-a | B1 − B3 | Linear | 0.247 | 2.077 | 1.548 | 0.203 |
| Exponential | 0.262 | 2.135 | 1.513 | 0.186 | ||
| Logarithmic | - | - | - | - | ||
| Second order polynomial | 0.263 | 2.055 | 1.497 | 0.170 | ||
| Power | - | - | - | - | ||
| TN | B1 + B4 | Linear | 0.579 | 3.001 | 2.519 | 0.645 |
| Exponential | 0.693 | 1.741 | 1.357 | 0.662 | ||
| Logarithmic | 0.669 | 1.598 | 1.303 | 0.597 | ||
| Second order polynomial | 0.688 | 1.556 | 1.316 | 0.616 | ||
| Power | 0.690 | 1.674 | 1.321 | 0.601 | ||
| TP | (B3 − B5)/(B3 + B5) | Linear | 0.545 | 0.055 | 0.039 | 0.376 |
| Exponential | 0.609 | 0.052 | 0.038 | 0.406 | ||
| Logarithmic | 0.615 | 0.050 | 0.035 | 0.413 | ||
| Second order polynomial | 0.630 | 0.049 | 0.034 | 0.416 | ||
| Power | 0.616 | 0.051 | 0.036 | 0.431 | ||
| CODMn | (B2 − B5)/(B2 + B5) | Linear | 0.120 | 0.579 | 0.482 | 0.107 |
| Exponential | 0.125 | 0.579 | 0.483 | 0.111 | ||
| Logarithmic | 0.154 | 0.568 | 0.478 | 0.143 | ||
| Second order polynomial | 0.209 | 0.549 | 0.453 | 0.204 | ||
| Power | 0.160 | 0.568 | 0.479 | 0.151 | ||
| Parameter | Modeling Formula | Training Dataset | Testing Dataset | ||
|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | ||
| Chl-a | y = 34.28 × (B1 − B3) + 3.09 | 0.247 | 2.077 | 1.548 | 0.203 |
| TN | y = 13.55e − 2.65 × (B1 + B4) | 0.693 | 1.741 | 1.357 | 0.662 |
| TP | 0.616 | 0.051 | 0.036 | 0.431 | |
| CODMn | 0.209 | 0.549 | 0.453 | 0.204 | |
| Parameter | Method | Training Dataset | Testing Dataset | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| Chl-a | MLR | 0.298 | 2.005 | 1.461 | 0.101 | 2.237 | 1.601 |
| Lasso | 0.247 | 2.086 | 1.520 | 0.203 | 2.079 | 1.544 | |
| BP | 0.288 | 2.021 | 1.468 | 0.122 | 2.210 | 1.569 | |
| RF | 0.762 | 1.393 | 1.087 | 0.317 | 1.943 | 1.505 | |
| XGBoost | 0.958 | 0.801 | 0.478 | 0.415 | 2.074 | 1.521 | |
| RF-BP | 0.991 | 0.224 | 0.169 | 0.341 | 2.112 | 1.613 | |
| BP-RF | 0.780 | 1.338 | 1.051 | 0.320 | 1.939 | 1.513 | |
| XGB-RF | 0.854 | 1.061 | 0.801 | 0.368 | 1.945 | 1.527 | |
| XGB-BP | 0.995 | 0.168 | 0.115 | 0.396 | 4.739 | 3.075 | |
| XGB-BP | 0.998 | 0.107 | 0.063 | 0.347 | 2.424 | 1.739 | |
| BP-XGB | 0.905 | 1.139 | 0.697 | 0.334 | 2.122 | 1.611 | |
| RF-XGB | 0.999 | 0.019 | 0.017 | 0.504 | 1.770 | 1.272 | |
| ML-MLR | 0.692 | 1.324 | 0.992 | 0.398 | 1.895 | 1.571 | |
| Parameter | Method | Training Dataset | Testing Dataset | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| TN | MLR | 0.589 | 1.760 | 1.415 | 0.644 | 1.458 | 1.266 |
| Lasso | 0.589 | 1.764 | 1.417 | 0.642 | 1.450 | 1.279 | |
| BP | 0.956 | 0.579 | 0.434 | 0.822 | 1.273 | 0.843 | |
| RF | 0.909 | 0.850 | 0.702 | 0.698 | 1.499 | 1.131 | |
| XGBoost | 0.946 | 1.057 | 0.842 | 0.708 | 1.326 | 1.034 | |
| RF-BP | 0.976 | 0.423 | 0.279 | 0.750 | 1.414 | 1.002 | |
| BP-RF | 0.977 | 0.430 | 0.293 | 0.839 | 1.189 | 0.632 | |
| XGB-RF | 0.941 | 0.686 | 0.545 | 0.708 | 1.494 | 1.036 | |
| BP-XGB | 0.951 | 0.678 | 0.516 | 0.831 | 1.089 | 0.707 | |
| RF-XGB | 0.910 | 0.959 | 0.750 | 0.700 | 1.385 | 1.042 | |
| ML-MLR | 0.958 | 0.564 | 0.423 | 0.819 | 1.280 | 0.866 | |
| Parameter | Method | Training Dataset | Testing Dataset | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| TP | MLR | 0.552 | 0.054 | 0.040 | 0.381 | 0.059 | 0.046 |
| Lasso | 0.545 | 0.055 | 0.040 | 0.376 | 0.057 | 0.047 | |
| BP | 0.626 | 0.051 | 0.037 | 0.432 | 0.053 | 0.045 | |
| RF | 0.913 | 0.026 | 0.018 | 0.350 | 0.061 | 0.044 | |
| XGBoost | 0.958 | 0.019 | 0.015 | 0.279 | 0.073 | 0.046 | |
| RF-BP | 0.880 | 0.031 | 0.022 | 0.347 | 0.062 | 0.042 | |
| XGB-BP | 0.835 | 0.035 | 0.026 | 0.311 | 0.063 | 0.046 | |
| BP-RF | 0.909 | 0.026 | 0.018 | 0.313 | 0.064 | 0.045 | |
| XGB-RF | 0.935 | 0.022 | 0.015 | 0.319 | 0.064 | 0.044 | |
| BP-XGB | 0.963 | 0.018 | 0.013 | 0.241 | 0.077 | 0.050 | |
| RF-XGB | 0.943 | 0.020 | 0.014 | 0.342 | 0.062 | 0.043 | |
| ML-MLR | 0.961 | 0.016 | 0.012 | 0.273 | 0.072 | 0.044 | |
| Parameter | Method | Training Dataset | Testing Dataset | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| CODMn | MLR | 0.152 | 0.569 | 0.479 | 0.060 | 0.832 | 0.710 |
| Lasso | 0.144 | 0.573 | 0.487 | 0.073 | 0.827 | 0.700 | |
| BP | 0.508 | 0.433 | 0.343 | 0.224 | 0.796 | 0.685 | |
| RF | 0.880 | 0.257 | 0.221 | 0.203 | 0.799 | 0.712 | |
| XGBoost | 0.911 | 0.280 | 0.220 | 0.113 | 0.860 | 0.794 | |
| RF-BP | 0.940 | 0.152 | 0.133 | 0.199 | 0.802 | 0.711 | |
| XGB-BP | 0.805 | 0.273 | 0.206 | 0.130 | 0.851 | 0.771 | |
| BP-RF | 0.903 | 0.219 | 0.178 | 0.272 | 0.767 | 0.674 | |
| XGB-RF | 0.915 | 0.198 | 0.164 | 0.172 | 0.824 | 0.732 | |
| BP-XGB | 0.961 | 0.181 | 0.115 | 0.192 | 0.825 | 0.744 | |
| RF-XGB | 0.980 | 0.115 | 0.091 | 0.142 | 0.827 | 0.715 | |
| ML-MLR | 0.884 | 0.210 | 0.174 | 0.190 | 0.816 | 0.723 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Guo, Y.; Yin, G.; Zhang, X.; Shi, Y.; Hao, F.; Fu, Y. UAV Multispectral Image-Based Urban River Water Quality Monitoring Using Stacked Ensemble Machine Learning Algorithms—A Case Study of the Zhanghe River, China. Remote Sens. 2022, 14, 3272. https://doi.org/10.3390/rs14143272
Xiao Y, Guo Y, Yin G, Zhang X, Shi Y, Hao F, Fu Y. UAV Multispectral Image-Based Urban River Water Quality Monitoring Using Stacked Ensemble Machine Learning Algorithms—A Case Study of the Zhanghe River, China. Remote Sensing. 2022; 14(14):3272. https://doi.org/10.3390/rs14143272
Chicago/Turabian StyleXiao, Yi, Yahui Guo, Guodong Yin, Xuan Zhang, Yu Shi, Fanghua Hao, and Yongshuo Fu. 2022. "UAV Multispectral Image-Based Urban River Water Quality Monitoring Using Stacked Ensemble Machine Learning Algorithms—A Case Study of the Zhanghe River, China" Remote Sensing 14, no. 14: 3272. https://doi.org/10.3390/rs14143272
APA StyleXiao, Y., Guo, Y., Yin, G., Zhang, X., Shi, Y., Hao, F., & Fu, Y. (2022). UAV Multispectral Image-Based Urban River Water Quality Monitoring Using Stacked Ensemble Machine Learning Algorithms—A Case Study of the Zhanghe River, China. Remote Sensing, 14(14), 3272. https://doi.org/10.3390/rs14143272