Middle- and Long-Term UT1-UTC Prediction Based on Constrained Polynomial Curve Fitting, Weighted Least Squares and Autoregressive Combination Model
Abstract
:1. Introduction
2. Methodology
2.1. Polynomial Curve Fitting
2.2. Weighted Least Squares
2.3. AR Model
2.4. Error Analysis
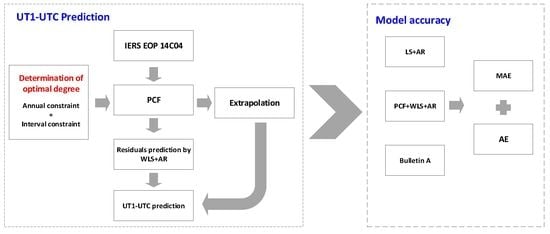
3. The Constrained PCF+WLS+AR Prediction Model
3.1. Data Description
3.2. Application of PCF in UT1R-TAI Modeling
3.2.1. Determination of Degree of PCF by Annual Constraint Method
3.2.2. Optimization of PCF Degree Using the Interval Constraint Method
3.3. The Processing of the Constrained PCF+WLS+AR Model
- (1)
- Determination of the PCF model.
- Based on the annual constraint method, the CV is calculated and compared with the annual prediction value to determine the initial optimal PCF degree;
- Optimize with interval constraints to obtain the final optimal PCF degree;
- Use the optimal degree for polynomial curve fitting and extrapolation.
- (2)
- Construction of WLS model.
- 4.
- Model the residuals of PCF and obtain the WLS extrapolation.
- (3)
- Residual prediction based on AR model.
- 5.
- Model the residuals of WLS.
- (4)
- UT1-UTC prediction using the combined PCF+WLS+AR model.
- 6.
- Add the leap seconds and solid Earth zonal tides.
4. Results and Discussion
- Case 1: UT1-UTC prediction based on the LS+AR model;
- Case 2: UT1-UTC prediction based on the constrained PCF+WLS+AR model (considering annual constraint);
- Case 3: UT1-UTC prediction based on the constrained PCF+WLS+AR model (considering annual constraint and interval constraint);
- Case 4: Bulletin A results achieved by IERS.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kalarus, M.; Schuh, H.; Kosek, W.; Akyilmaz, O.; Bizouard, C.; Gambis, D.; Gross, R.; Jovanović, B.; Kumakshev, S.; Kutterer, H.; et al. Achievements of the Earth orientation parameters prediction comparison campaign. J. Geod. 2010, 84, 587–596. [Google Scholar] [CrossRef]
- Schuh, H.; Ulrich, M.; Egger, D.; Müller, J.; Schwegmann, W. Prediction of Earth orientation parameters by artificial neural networks. J. Geod. 2002, 76, 247–258. [Google Scholar] [CrossRef]
- Schuh, H.; Behrend, D. VLBI: A fascinating technique for geodesy and astrometry. J. Geodyn. 2012, 61, 68–80. [Google Scholar] [CrossRef] [Green Version]
- Pearlman, M.R.; Degnan, J.J.; Bosworth, J.M. The international laser ranging service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]
- Hein, G.W. Status, perspectives and trends of satellite navigation. Satell. Navig. 2020, 1, 22. [Google Scholar] [CrossRef]
- Willis, P.; Fagard, H.; Ferrage, P.; Lemoine, F.G.; Noll, C.E.; Noomen, R.; Otten, M.; Ries, J.C.; Rothacher, M.; Soudarin, L. The international DORIS service (IDS): Toward maturity. Adv. Space Res. 2010, 45, 1408–1420. [Google Scholar] [CrossRef]
- Gambis, D. Monitoring Earth orientation using space-geodetic techniques: State-of-the-art and prospective. J. Geod. 2004, 78, 295–303. [Google Scholar] [CrossRef]
- Nilsson, T.; Heinkelmann, R.; Karbon, M.; Raposo-Pulido, V.; Soja, B.; Schuh, H. Earth orientation parameters estimated from VLBI during the CONT11 campaign. J. Geod. 2014, 88, 491–502. [Google Scholar] [CrossRef]
- Gross, R.S.; Marcus, S.L.; Eubanks, T.M.; Dickey, J.O.; Keppenne, C.L. Detection of an ENSO signal in seasonal length-of-day variations. Geophys. Res. Lett. 1996, 23, 3373–3376. [Google Scholar] [CrossRef]
- Kosek, W.; Kalarus, M.; Johnson, T.; Wooden, W.; McCarthy, D.; Popinski, W. A comparison of UT1-UTC forecasts by different prediction techniques. Proc. Journeys Syst. Ref. Spatiotemporal 2004, 140–141. [Google Scholar]
- Niedzielski, T.; Kosek, W. Prediction of UT1–UTC, LOD and AAM χ3 by combination of least-squares and multivariate stochastic methods. J. Geod. 2007, 82, 83–92. [Google Scholar] [CrossRef]
- McCarthy, D.D.; Petit, G. IERS Conventions (2003); International Earth Rotation And Reference Systems Service (IERS): Cologne, Germany, 2004. [Google Scholar]
- Kosek, W.; Kalarus, M.; Johnson, T.; Wooden, W.; McCarthy, D.; Popinski, W. A comparison of LOD and UT1-UTC forecasts by different combined prediction techniques. Artif Satell 2005, 40, 119–125. [Google Scholar]
- Kosek, W.; McCarthy, D.; Luzum, B. Possible improvement of Earth orientation forecast using autocovariance prediction procedures. J. Geod. 1998, 72, 189–199. [Google Scholar] [CrossRef]
- Gross, R.S.; Eubanks, T.M.; Steppe, J.A.; Freedman, A.P.; Dickey, J.O.; Runge, T.F. A Kalman-filter-based approach to combining independent Earth-orientation series. J. Geod. 1998, 72, 215–235. [Google Scholar] [CrossRef]
- Kosek, W. Future Improvements in EOP Prediction; Springer: Berlin/Heidelberg, Germany, 2012; pp. 513–520. [Google Scholar]
- Xu, X.Q.; Zhou, Y.H.; Liao, X.H. Short-term earth orientation parameters predictions by combination of the least-squares, AR model and Kalman filter. J. Geodyn. 2012, 62, 83–86. [Google Scholar] [CrossRef]
- Dill, R.; Dobslaw, H.; Thomas, M. Improved 90-day Earth orientation predictions from angular momentum forecasts of atmosphere, ocean, and terrestrial hydrosphere. J. Geod. 2018, 93, 287–295. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Wilson, C. Hydrological excitations of polar motion, 1993–2002. Geophys. J. Int. 2005, 160, 833–839. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Guo, J.Y.; Liu, X.; Kong, Q.L.; Guo, L.X.; Li, W. Long-term prediction of polar motion using a combined SSA and ARMA model. J. Geod. 2018, 92, 333–343. [Google Scholar] [CrossRef]
- Zheng, D.; Chao, B.; Zhou, Y.; Yu, N. Improvement of edge effect of the wavelet time–frequency spectrum: Application to the length-of-day series. J. Geod. 2000, 74, 249–254. [Google Scholar] [CrossRef]
- Burden, R.L.; Faires, J.D.; Burden, A.M. Numerical Analysis; Cengage Learning: Boston, MA, USA, 2015. [Google Scholar]
- Keren, D.; Gotsman, C. Fitting curves and surfaces with constrained implicit polynomials. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 31–41. [Google Scholar] [CrossRef] [Green Version]
- Peck, J. Polynomial curve fitting with constraint. SIAM Rev. 1962, 4, 135–141. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, T. Prediction of earth rotation parameters based on improved weighted least squares and autoregressive model. Geod. Geodyn. 2012, 3, 57–64. [Google Scholar]
- Weisstein, E.W. Least Squares Fitting. 2002. Available online: https://mathworld.wolfram.com/ (accessed on 10 July 2020).
- Cohen, A.; Migliorati, G. Optimal weighted least-squares methods. SMAI J. Comput. Math. 2017, 3, 181–203. [Google Scholar] [CrossRef]
- Bizouard, C.; Lambert, S.; Gattano, C.; Becker, O.; Richard, J.-Y. The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014. J. Geod. 2019, 93, 621–633. [Google Scholar] [CrossRef]
- Jia, S.; Xu, T.H.; Sun, Z.Z.; Li, J.J. Middle and long-term prediction of UT1-UTC based on combination of Gray Model and Autoregressive Integrated Moving Average. Adv. Space Res. 2017, 59, 888–894. [Google Scholar] [CrossRef]
- Modiri, S.; Belda, S.; Hoseini, M.; Heinkelmann, R.; Ferrándiz, J.M.; Schuh, H. A new hybrid method to improve the ultra-short-term prediction of LOD. J. Geod. 2020, 94, 23. [Google Scholar] [CrossRef] [Green Version]
- Bigun, J. Optimal Orientation Detection of Linear Symmetry; Linköping University Electronic Press: Linköping, Sweden, 1987. [Google Scholar]












| Time | Optimal Degree of PCF by Annual Constraint | True/False |
|---|---|---|
| 1 January 2014 | 4 | T |
| 1 July 2014 | 4 | T |
| 1 January 2015 | 4 | T |
| 1 July 2015 | 5 | T |
| 1 January 2016 | 5 | T |
| 1 July 2016 | 5 | T |
| 1 January 2017 | 5 | T |
| 1 July 2017 | 5 | T |
| 1 January 2018 | 4 | F |
| 1 July 2018 | 4 | T |
| Span | Case 1 | Case 2 | Case 3 | Case 4 | Improvement |
|---|---|---|---|---|---|
| 1 | 0.036 | 0.037 | 0.036 | 0.056 | 35.5% |
| 10 | 1.049 | 1.124 | 1.083 | 0.452 | −139.4% |
| 20 | 2.460 | 2.749 | 2.596 | 1.601 | −62.1% |
| 30 | 3.544 | 4.151 | 3.802 | 2.910 | −30.7% |
| 60 | 7.396 | 8.722 | 7.616 | 7.284 | −4.6% |
| 90 | 12.390 | 13.191 | 11.332 | 11.271 | −0.5% |
| 120 | 18.338 | 17.867 | 15.077 | 15.626 | 3.5% |
| 180 | 33.148 | 29.346 | 23.954 | 25.962 | 7.7% |
| 240 | 51.349 | 41.785 | 33.250 | 39.485 | 15.8% |
| 300 | 71.272 | 52.021 | 40.979 | 56.666 | 27.7% |
| 360 | 92.197 | 65.819 | 50.934 | 76.217 | 33.2% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Xu, T.; Sun, Z.; Nie, W.; Fang, Z. Middle- and Long-Term UT1-UTC Prediction Based on Constrained Polynomial Curve Fitting, Weighted Least Squares and Autoregressive Combination Model. Remote Sens. 2022, 14, 3252. https://doi.org/10.3390/rs14143252
Yang Y, Xu T, Sun Z, Nie W, Fang Z. Middle- and Long-Term UT1-UTC Prediction Based on Constrained Polynomial Curve Fitting, Weighted Least Squares and Autoregressive Combination Model. Remote Sensing. 2022; 14(14):3252. https://doi.org/10.3390/rs14143252
Chicago/Turabian StyleYang, Yuguo, Tianhe Xu, Zhangzhen Sun, Wenfeng Nie, and Zhenlong Fang. 2022. "Middle- and Long-Term UT1-UTC Prediction Based on Constrained Polynomial Curve Fitting, Weighted Least Squares and Autoregressive Combination Model" Remote Sensing 14, no. 14: 3252. https://doi.org/10.3390/rs14143252
APA StyleYang, Y., Xu, T., Sun, Z., Nie, W., & Fang, Z. (2022). Middle- and Long-Term UT1-UTC Prediction Based on Constrained Polynomial Curve Fitting, Weighted Least Squares and Autoregressive Combination Model. Remote Sensing, 14(14), 3252. https://doi.org/10.3390/rs14143252