A Continuous Change Tracker Model for Remote Sensing Time Series Reconstruction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
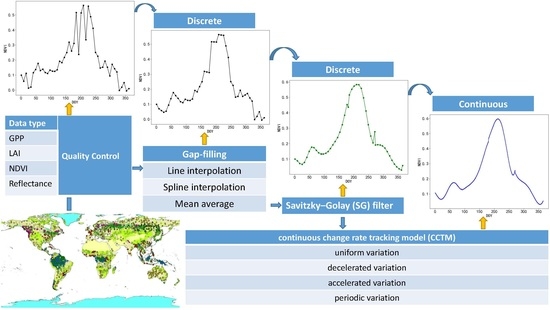
2.2. Time Series Reconstruction Flow
2.3. Data Preprocessing
2.3.1. Points Sampling and Quality Control
2.3.2. Gap Filling
2.3.3. Enhanced SG Filtering
2.4. Model Fitting
2.4.1. CCTM Model
2.4.2. Two Patterns of the CCTM Model
2.4.3. Comparison Models
2.4.4. Evaluation of Time Series Reconstruction Accuracy
2.4.5. Accuracy Validation of Yearly and Seasonal Time Series Patterns
3. Results
3.1. Comparison of Yearly Timeseries Pattern
3.2. Reconstruction with Seasonal Segment Time-Series Fitting
3.2.1. Smoothing Process
3.2.2. Reconstruction with Smoothing Process by Seasonal Segment Fitting
4. Discussion
4.1. Advantages and Limitations
4.2. Potential Applications
4.3. Time Series Functionalization and Compression
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ehrlich, D.; Estes, J.E.; Singh, A. Applications of NOAA-AVHRR 1 km data for environmental monitoring. Int. J. Remote Sens. 1994, 15, 145–161. [Google Scholar] [CrossRef]
- Schepaschenko, D.; Chave, J.; Phillips, O.L.; Lewis, S.L.; Davies, S.J.; Réjou-Méchain, M.; Sist, P.; Scipal, K.; Perger, C.; Herault, B.; et al. The Forest Observation System, building a global reference dataset for remote sensing of forest biomass. Sci. Data 2019, 6, 198. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barnes, W.; Xiong, X.; Salomonson, V. Status of terra MODIS and aqua modis. Adv. Space Res. 2003, 32, 2099–2106. [Google Scholar] [CrossRef]
- Irons, J.R.; Dwyer, J.; Barsi, J.A. The next Landsat satellite: The Landsat Data Continuity Mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar] [CrossRef] [Green Version]
- Kuenzer, C.; Ottinger, M.; Wegmann, M.; Guo, H.; Wang, C.; Zhang, J.; Dech, S.; Wikelski, M. Earth observation satellite sensors for biodiversity monitoring: Potentials and bottlenecks. Int. J. Remote Sens. 2014, 35, 6599–6647. [Google Scholar] [CrossRef] [Green Version]
- Kuenzer, C.; Dech, S.; Wagner, W. Remote sensing time series revealing land surface dynamics: Status quo and the pathway ahead. In Remote Sensing Time Series; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–24. [Google Scholar]
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H.; et al. A long-term Global LAnd Surface Satellite (GLASS) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Tuia, D.; Ratle, F.; Pacifici, F.; Kanevski, M.; Emery, W. Active Learning Methods for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2218–2232. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E.; Holden, C.; Yang, Z. Generating synthetic Landsat images based on all available Landsat data: Predicting Landsat surface reflectance at any given time. Remote Sens. Environ. 2015, 162, 67–83. [Google Scholar] [CrossRef]
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing Information Reconstruction of Remote Sensing Data: A Technical Review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Tian, H.; Wang, Y.; Chen, T.; Zhang, L.; Qin, Y. Early-Season Mapping of Winter Crops Using Sentinel-2 Optical Imagery. Remote Sens. 2021, 13, 3822. [Google Scholar] [CrossRef]
- Tian, H.; Qin, Y.; Niu, Z.; Wang, L.; Ge, S. Summer Maize Mapping by Compositing Time Series Sentinel-1A Imagery Based on Crop Growth Cycles. J. Indian Soc. Remote Sens. 2021, 49, 2863–2874. [Google Scholar] [CrossRef]
- Tian, H.; Chen, T.; Li, Q.; Mei, Q.; Wang, S.; Yang, M.; Wang, Y.; Qin, Y. A Novel Spectral Index for Automatic Canola Mapping by Using Sentinel-2 Imagery. Remote Sens. 2022, 14, 1113. [Google Scholar] [CrossRef]
- Li, S.; Xu, L.; Jing, Y.; Yin, H.; Li, X.; Guan, X. High-quality vegetation index product generation: A review of NDVI time series reconstruction techniques. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102640. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Roy, D.P. Investigation of the maximum Normalized Difference Vegetation Index (NDVI) and the maximum surface temperature (Ts) AVHRR compositing procedures for the extraction of NDVI and Ts over forest. Int. J. Remote Sens. 1997, 18, 2383–2401. [Google Scholar] [CrossRef]
- Taddei, R. Maximum Value Interpolated (MVI): A Maximum Value Composite method improvement in vegetation index profiles analysis. Int. J. Remote Sens. 1997, 18, 2365–2370. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A. Comparison of cloud-reconstruction methods for time series of composite NDVI data. Remote Sens. Environ. 2010, 114, 618–625. [Google Scholar] [CrossRef]
- Wenwen, C.; Jinling, S.; Jindi, W.; Zhiqiang, X. High spatial-and temporal-resolution NDVI produced by the assimilation of MODIS and HJ-1 data. Can. J. Remote Sens. 2011, 37, 327–612. [Google Scholar] [CrossRef]
- Gu, J.; Li, X.; Huang, C.; Okin, G. A simplified data assimilation method for reconstructing time-series MODIS NDVI data. Adv. Space Res. 2009, 44, 501–509. [Google Scholar] [CrossRef]
- Gu, J.; Li, X.; Huang, C. Spatio-Temporal Reconstruction of MODIS NDVI Data Sets Based on Data Assimilation Methods. In Proceedings of the 8th International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences, Shanghai, China, 25–27 June 2008; pp. 242–247. [Google Scholar]
- Lange, M.; DeChant, B.; Rebmann, C.; Vohland, M.; Cuntz, M.; Doktor, D. Validating MODIS and Sentinel-2 NDVI Products at a Temperate Deciduous Forest Site Using Two Independent Ground-Based Sensors. Sensors 2017, 17, 1855. [Google Scholar] [CrossRef] [Green Version]
- Viovy, N.; Arino, O.; Belward, A.S. The Best Index Slope Extraction ( BISE): A method for reducing noise in NDVI time-series. Int. J. Remote Sens. 1992, 13, 1585–1590. [Google Scholar] [CrossRef]
- Liu, R.; Shang, R.; Liu, Y.; Lu, X. Global evaluation of gap-filling approaches for seasonal NDVI with considering vegetation growth trajectory, protection of key point, noise resistance and curve stability. Remote Sens. Environ. 2016, 189, 164–179. [Google Scholar] [CrossRef] [Green Version]
- Lovell, J.L.; Graetz, R.D. Filtering pathfinder AVHRR land NDVI data for Australia. Int. J. Remote Sens. 2001, 22, 2649–2654. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Chen, Y.; Cao, R.; Chen, J.; Liu, L.; Matsushita, B. A practical approach to reconstruct high-quality Landsat NDVI time-series data by gap filling and the Savitzky–Golay filter. ISPRS J. Photogramm. Remote Sens. 2021, 180, 174–190. [Google Scholar] [CrossRef]
- Zhao, A.-X.; Tang, X.-J.; Zhang, Z.-H.; Liu, J.-H. The parameters optimization selection of Savitzky-Golay filter and its application in smoothing pretreatment for FTIR spectra. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2014; pp. 516–521. [Google Scholar]
- Luo, J.; Ying, K.; Bai, J. Savitzky–Golay smoothing and differentiation filter for even number data. Signal Process. 2005, 85, 1429–1434. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Lu, X.; Liu, R.; Liu, J.; Liang, S. Removal of Noise by Wavelet Method to Generate High Quality Temporal Data of Terrestrial MODIS Products. Photogramm. Eng. Remote Sens. 2007, 73, 1129–1139. [Google Scholar] [CrossRef] [Green Version]
- Beck, P.S.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ. 2006, 100, 321–334. [Google Scholar] [CrossRef]
- Sellers, P.J.; Tucker, C.J.; Collatz, G.J.; Los, S.O.; Justice, C.O.; Dazlich, D.A.; Randall, D.A. A Global 1-Degrees by 1-Degrees Ndvi Data Set for Climate Studies. The Generation of Global Fields of Terrestrial Biophysical Parameters from the Ndvi (Vol 15, Pg 3519, 1995). Int. J. Remote Sens. 1995, 16, 1571. [Google Scholar]
- Chen, J.; Deng, F.; Chen, M. Locally adjusted cubic-spline capping for reconstructing seasonal trajectories of a satellite-derived surface parameter. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2230–2238. [Google Scholar] [CrossRef]
- Yang, G.; Shen, H.; Zhang, L.; He, Z.; Li, X. A Moving Weighted Harmonic Analysis Method for Reconstructing High-Quality SPOT VEGETATION NDVI Time-Series Data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6008–6021. [Google Scholar] [CrossRef]
- Roerink, G.J.; Menenti, M.; Verhoef, W. Reconstructing cloudfree NDVI composites using Fourier analysis of time series. Int. J. Remote Sens. 2000, 21, 1911–1917. [Google Scholar] [CrossRef]
- Zhou, J.; Jia, L.; Menenti, M.; Liu, X. Optimal Estimate of Global Biome—Specific Parameter Settings to Reconstruct NDVI Time Series with the Harmonic ANalysis of Time Series (HANTS) Method. Remote Sens. 2021, 13, 4251. [Google Scholar] [CrossRef]
- Zhou, J.; Jia, L.; van Hoek, M.; Menenti, M.; Lu, J.; Hu, G. An optimization of parameter settings in HANTS for global NDVI time series reconstruction. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3422–3425. [Google Scholar]
- Zhou, J.; Jia, L.; Menenti, M. Reconstruction of global MODIS NDVI time series: Performance of Harmonic ANalysis of Time Series (HANTS). Remote Sens. Environ. 2015, 163, 217–228. [Google Scholar] [CrossRef]
- Xu, L.; Li, B.; Yuan, Y.; Gao, X.; Zhang, T. A Temporal-Spatial Iteration Method to Reconstruct NDVI Time Series Datasets. Remote Sens. 2015, 7, 8906–8924. [Google Scholar] [CrossRef] [Green Version]
- Cao, R.; Chen, Y.; Shen, M.; Chen, J.; Zhou, J.; Wang, C.; Yang, W. A simple method to improve the quality of NDVI time-series data by integrating spatiotemporal information with the Savitzky-Golay filter. Remote Sens. Environ. 2018, 217, 244–257. [Google Scholar] [CrossRef]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Ma, M.; Veroustraete, F. Reconstructing pathfinder AVHRR land NDVI time-series data for the Northwest of China. Adv. Space Res. 2006, 37, 835–840. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef] [Green Version]
- Madden, H.H. Comments on the Savitzky-Golay convolution method for least-squares-fit smoothing and differentiation of digital data. Anal. Chem. 1978, 50, 1383–1386. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Woodcock, C.E.; Olofsson, P. Continuous monitoring of forest disturbance using all available Landsat imagery. Remote Sens. Environ. 2012, 122, 75–91. [Google Scholar] [CrossRef]
- Liu, J.; Liu, M.; Tian, H.; Zhuang, D.; Zhang, Z.; Zhang, W.; Tang, X.; Deng, X. Spatial and temporal patterns of China’s cropland during 1990–2000: An analysis based on Landsat TM data. Remote Sens. Environ. 2005, 98, 442–456. [Google Scholar] [CrossRef]
- Lausch, A.; Erasmi, S.; King, D.J.; Magdon, P.; Heurich, M. Understanding Forest Health with Remote Sensing -Part I—A Review of Spectral Traits, Processes and Remote-Sensing Characteristics. Remote Sens. 2016, 8, 1029. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Hill, M.J.; Zhang, X.; Wang, Z.; Richardson, A.D.; Hufkens, K.; Filippa, G.; Baldocchi, D.D.; Ma, S.; Verfaillie, J.; et al. Using data from Landsat, MODIS, VIIRS and PhenoCams to monitor the phenology of California oak/grass savanna and open grassland across spatial scales. Agric. For. Meteorol. 2017, 237–238, 311–325. [Google Scholar] [CrossRef]
- Katznelson, Y. An Introduction to Harmonic Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]











| Dataset | Date | URL | Description |
|---|---|---|---|
| MCD15A3H (MODIS Leaf Area Index/FPAR 4-Day Global 500 m) | 2001–2005 | https://developers.google.com/earth-engine/datasets/catalog/MODIS_006_MCD15A3H (accessed on 21 April 2022) | The MCD15A3H V6 level 4, Combined Fraction of Photosynthetically Active Radiation (FPAR), and Leaf Area Index (LAI) product is a 4-day composite data set with 500 m pixel size. |
| MOD17A2H (Terra Gross Primary Productivity 8-Day Global 500 M) | 2001–2005 | https://developers.google.com/earth-engine/datasets/catalog/MODIS_006_MOD17A2H (accessed on 21 April 2022) | The MOD17A2H V6 Gross Primary Productivity (GPP) product is a cumulative 8-day composite with a 500 m resolution. |
| MOD09Q1 (Terra Surface Reflectance 8-Day Global 250 m) | 2001–2005 | https://developers.google.com/earth-engine/datasets/catalog/MODIS_006_MOD09Q1 (accessed on 21 April 2022) | The MOD09Q1 product provides an estimate of the surface spectral reflectance of bands 1 and 2 at 250 m resolution and corrected for atmospheric conditions such as gasses, aerosols, and Rayleigh scattering. |
| Data type | GPP | |||||||
| land cover | Grassland | Cropland | DBF | EBF | ENF | MF | Savannas | Shrubland |
| R2 (>0.9) | 99 | 97 | 100 | 93 | 100 | 100 | 99 | 96 |
| RMSE (<5) | 99 | 99 | 93 | 64 | 97 | 97 | 97 | 100 |
| num_points | 985 | 985 | 490 | 485 | 480 | 490 | 470 | 980 |
| Data type | NDVI | |||||||
| landcover | Grassland | Cropland | DBF | EBF | ENF | MF | Savannas | Shrubland |
| R2 (>0.9) | 95 | 90 | 100 | 33 | 94 | 98 | 94 | 86 |
| RMSE (>0.01) | 96 | 99 | 100 | 99 | 100 | 100 | 100 | 79 |
| num_points | 945 | 842 | 481 | 202 | 415 | 470 | 446 | 977 |
| Data type | LAI | |||||||
| landcover | Grassland | Cropland | DBF | EBF | ENF | MF | Savannas | Shrubland |
| R2 (>0.9) | 98 | 97 | 97 | 93 | 98 | 98 | 97 | 97 |
| RMSE (<0.5) | 100 | 100 | 91 | 70 | 94 | 92 | 98 | 100 |
| num_points | 979 | 831 | 490 | 490 | 480 | 490 | 485 | 923 |
| Data type | MSR | |||||||
| landcover | Grassland | Cropland | DBF | EBF | ENF | MF | Savannas | Shrubland |
| R2 (>0.9) | 91 | 96 | 99 | 94 | 98 | 99 | 97 | 67 |
| RMSE (<0.035) | 91 | 97 | 99 | 99 | 99 | 98 | 92 | 93 |
| num_points | 817 | 736 | 440 | 142 | 374 | 395 | 382 | 730 |
| Data Type | Models | Ln | Harmonic | Exp | CCTM | Num Points | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| GPP | landcover | R2 (>0.98) | RMSE (<2) | R2 (>0.98) | RMSE (<2) | R2 (>0.98) | RMSE (<2) | R2 (>0.98) | RMSE (<2) | |
| Grassland | 83 | 98 | 96 | 97 | 84 | 95 | 99 | 100 | 995 | |
| Cropland | 64 | 92 | 85 | 86 | 65 | 79 | 94 | 98 | 990 | |
| DBF | 87 | 89 | 97 | 66 | 90 | 65 | 88 | 99 | 500 | |
| EBF | 28 | 41 | 65 | 28 | 29 | 18 | 85 | 81 | 485 | |
| ENF | 97 | 97 | 99 | 72 | 97 | 77 | 100 | 100 | 500 | |
| MF | 95 | 94 | 99 | 62 | 95 | 70 | 100 | 99 | 500 | |
| Savannas | 78 | 92 | 94 | 82 | 79 | 80 | 98 | 99 | 500 | |
| Shrubland | 79 | 100 | 92 | 99 | 80 | 100 | 98 | 100 | 990 | |
| LAI | landcover | R2 (>0.9) | RMSE (<0.5) | R2 (>0.9) | RMSE (<0.5) | R2 (>0.9) | RMSE (<0.5) | R2 (>0.9) | RMSE (<0.5) | |
| Grassland | 95 | 99 | 99 | 100 | 96 | 99 | 97 | 100 | 934 | |
| Cropland | 86 | 98 | 98 | 99 | 89 | 98 | 92 | 99 | 880 | |
| DBF | 96 | 84 | 99 | 95 | 97 | 86 | 99 | 91 | 480 | |
| EBF | 61 | 34 | 91 | 57 | 67 | 31 | 75 | 48 | 438 | |
| ENF | 88 | 85 | 99 | 93 | 91 | 84 | 93 | 89 | 482 | |
| MF | 91 | 83 | 99 | 94 | 94 | 83 | 96 | 89 | 493 | |
| Savannas | 90 | 97 | 98 | 97 | 93 | 96 | 94 | 97 | 470 | |
| Shrubland | 92 | 100 | 98 | 100 | 93 | 100 | 96 | 100 | 976 | |
| NDVI | landcover | R2 (>0.995) | RMSE (<0.02) | R2 (>0.995) | RMSE (<0.02) | R2 (>0.995) | RMSE (<0.02) | R2 (>0.995) | RMSE (<0.02) | |
| Grassland | 65 | 97 | 34 | 97 | 29 | 96 | 98 | 98 | 956 | |
| Cropland | 55 | 98 | 28 | 96 | 21 | 94 | 96 | 99 | 987 | |
| DBF | 90 | 94 | 55 | 93 | 49 | 91 | 100 | 99 | 491 | |
| EBF | 6 | 99 | 0 | 97 | 0 | 95 | 59 | 100 | 204 | |
| ENF | 61 | 85 | 31 | 88 | 25 | 75 | 95 | 96 | 421 | |
| MF | 76 | 84 | 43 | 89 | 35 | 76 | 98 | 95 | 475 | |
| Savannas | 75 | 92 | 37 | 88 | 30 | 83 | 98 | 98 | 456 | |
| Shrubland | 57 | 91 | 21 | 85 | 15 | 84 | 94 | 94 | 987 | |
| MSR | landcover | R2 (>0.995) | RMSE (<0.01) | R2 (>0.995) | RMSE (<0.01) | R2 (>0.995) | RMSE (<0.01) | R2 (>0.995) | RMSE (<0.01) | |
| Grassland | 19 | 76 | 39 | 73 | 18 | 71 | 58 | 87 | 827 | |
| Cropland | 9 | 87 | 30 | 85 | 8 | 84 | 54 | 96 | 678 | |
| DBF | 27 | 94 | 54 | 92 | 27 | 89 | 77 | 99 | 447 | |
| EBF | 1 | 99 | 8 | 99 | 1 | 99 | 31 | 99 | 142 | |
| ENF | 27 | 90 | 66 | 90 | 28 | 86 | 85 | 97 | 377 | |
| MF | 32 | 90 | 67 | 86 | 36 | 83 | 81 | 95 | 396 | |
| Savannas | 23 | 70 | 64 | 97 | 27 | 61 | 74 | 85 | 827 | |
| Shrubland | 12 | 83 | 23 | 81 | 11 | 81 | 46 | 90 | 678 | |
| Dataset | 8-Day Time Series NDVI | Daily Time Series Reflectance | |
|---|---|---|---|
| Compression pattern | seasonal | yearly | seasonal |
| Coefficient number | 24 | 6 | 24 |
| Original storage (MB) | 20.63 | 21 | 163.7 |
| Compressed storage (MB) | 10.7 | 2.7 | 10.7 |
| R2 | 0.99 | 1 | 0.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, L.; He, Y.; Huang, N.; Li, W.; Xu, S.; Zhou, Q.; Song, W.; Duan, W.; Wang, X.; et al. A Continuous Change Tracker Model for Remote Sensing Time Series Reconstruction. Remote Sens. 2022, 14, 2280. https://doi.org/10.3390/rs14092280
Zhang Y, Wang L, He Y, Huang N, Li W, Xu S, Zhou Q, Song W, Duan W, Wang X, et al. A Continuous Change Tracker Model for Remote Sensing Time Series Reconstruction. Remote Sensing. 2022; 14(9):2280. https://doi.org/10.3390/rs14092280
Chicago/Turabian StyleZhang, Yangjian, Li Wang, Yuanhuizi He, Ni Huang, Wang Li, Shiguang Xu, Quan Zhou, Wanjuan Song, Wensheng Duan, Xiaoyue Wang, and et al. 2022. "A Continuous Change Tracker Model for Remote Sensing Time Series Reconstruction" Remote Sensing 14, no. 9: 2280. https://doi.org/10.3390/rs14092280
APA StyleZhang, Y., Wang, L., He, Y., Huang, N., Li, W., Xu, S., Zhou, Q., Song, W., Duan, W., Wang, X., Muhammad, S., Nath, B., Zhu, L., Tang, F., Du, H., Wang, L., & Niu, Z. (2022). A Continuous Change Tracker Model for Remote Sensing Time Series Reconstruction. Remote Sensing, 14(9), 2280. https://doi.org/10.3390/rs14092280