Radiative Transfer Image Simulation Using L-System Modeled Strawberry Canopies
Abstract
:1. Introduction
2. Methods
2.1. Study Site and Data Collection
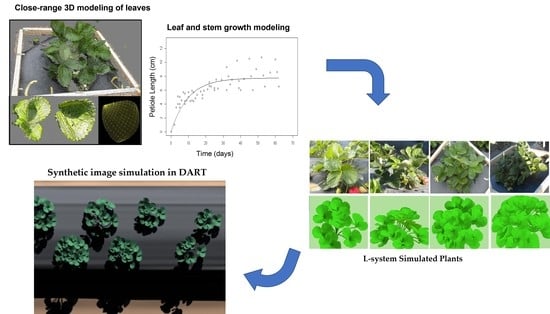
2.2. Simulation of Plant Growth Using L-System
2.3. Radiative Transfer Image Simulation
3. Results
3.1. L-System Canopy Growth Simulation Results
3.2. Radiative Transfer Image Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A



References
- Gibbs, J.A.; Pound, M.; French, A.P.; Wells, D.M.; Murchie, E.; Pridmore, T. Approaches to three-dimensional reconstruction of plant shoot topology and geometry. Funct. Plant Biol. 2017, 44, 62–75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, G.; Jiang, H.; Luo, J.; Mu, X.; Li, F.; Qi, J.; Hu, R.; Xie, D.; Zhou, G. Quantitative Evaluation of Leaf Inclination Angle Distribution on Leaf Area Index Retrieval of Coniferous Canopies. J. Remote Sens. 2021, 2021, 2708904. [Google Scholar] [CrossRef]
- Gauthier, M.; Barillot, R.; Schneider, A.; Chambon, C.; Fournier, C.; Pradal, C.; Robert, C.; Andrieu, B. A functional structural model of grass development based on metabolic regulation and coordination rules. J. Exp. Bot. 2020, 71, 5454–5468. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Cimen, E.; Singh, N.; Buckler, E. Deep learning for plant genomics and crop improvement. Curr. Opin. Plant Biol. 2020, 54, 34–41. [Google Scholar] [CrossRef] [PubMed]
- Auzmendi, I.; Hanan, J.S. Investigating tree and fruit growth through functional–structural modelling: Implications of carbon autonomy at different scales. Ann. Bot. 2020, 126, 775–788. [Google Scholar] [CrossRef] [PubMed]
- Ubbens, J.; Cieslak, M.; Prusinkiewicz, P.; Stavness, I. The use of plant models in deep learning: An application to leaf counting in rosette plants. Plant Methods 2018, 14, 6. [Google Scholar] [CrossRef] [Green Version]
- Giavitto, J.-L.; Michel, O. MGS: A Programming Language for the Transformations of Topological Collections; Technical Report 61-2001; LaMI–Université d’Évry Val d’Essonne: Évry, France, 2011. [Google Scholar]
- Lindenmayer, A. Mathematical models for cellular interactions in development I. Filaments with one-sided inputs. J. Theor. Biol. 1968, 18, 280–299. [Google Scholar] [CrossRef]
- Prusinkiewicz, P.; Lindenmayer, A. The Algorithmic Beauty of Plants; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Benoit, L.; Rousseau, D.; Belin, É.; Demilly, D.; Chapeau-Blondeau, F. Simulation of image acquisition in machine vision dedicated to seedling elongation to validate image processing root segmentation algorithms. Comput. Electron. Agr. 2014, 104, 84–92. [Google Scholar] [CrossRef] [Green Version]
- Rokhana, R.; Herulambang, W.; Indraswari, R. Machine Learning and Polynomial–L System Algorithm for Modeling and Simulation of Glycine Max (L) Merrill Growth. In Proceedings of the 2020 International Electronics Symposium (IES), Surabaya, Indonesia, 29–30 September 2020; pp. 463–467. [Google Scholar]
- Xin, B.; Liu, S.; Whitty, M. Three-dimensional reconstruction of Vitis vinifera (L.) cvs Pinot Noir and Merlot grape bunch frameworks using a restricted reconstruction grammar based on the stochastic L-system. Aust. J. Grape Wine Res. 2020, 26, 207–219. [Google Scholar] [CrossRef]
- Neubert, B.; Franken, T.; Deussen, O. Approximate image-based tree-modeling using particle flows. ACM Trans. Graph. 2007, 26, 88. [Google Scholar] [CrossRef]
- Okabe, M.; Owada, S.; Igarash, T. Interactive Design of Botanical Trees using Freehand Sketches and Example-based Editing. Comput. Graph. Forum 2005, 24, 487–496. [Google Scholar] [CrossRef]
- Westoby, M.; Brasington, J.; Glasser, N.; Hambrey, M.; Reynolds, J. ‘Structure-from-Motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef] [Green Version]
- Livny, Y.; Yan, F.; Olson, M.; Chen, B.; Zhang, H.; El-Sana, J. Automatic reconstruction of tree skeletal structures from point clouds. In Proceedings of the ACM SIGGRAPH Asia 2010 papers, Seoul, South Korea, 15 December 2010; pp. 1–8. [Google Scholar]
- Quan, L.; Tan, P.; Zeng, G.; Yuan, L.; Wang, J.; Kang, S.B. Image-based plant modeling. ACM Trans. Graph. 2006, 25, 599–604. [Google Scholar] [CrossRef]
- Tan, P.; Zeng, G.; Wang, J.; Kang, S.B.; Quan, L. Image-based tree modeling. ACM Trans. Graph. 2007, 26, 87. [Google Scholar] [CrossRef]
- Xu, H.; Gossett, N.; Chen, B. Knowledge and heuristic-based modeling of laser-scanned trees. ACM Trans. Graph. 2007, 26, 19. [Google Scholar] [CrossRef]
- Abd-Elrahman, A.; Guan, Z.; Dalid, C.; Whitaker, V.; Britt, K.; Wilkinson, B.; Gonzalez, A. Automated Canopy Delineation and Size Metrics Extraction for Strawberry Dry Weight Modeling Using Raster Analysis of High-Resolution Imagery. Remote Sens. 2020, 12, 3632. [Google Scholar] [CrossRef]
- Guan, Z.; Abd-Elrahman, A.; Fan, Z.; Whitaker, V.M.; Wilkinson, B. Modeling strawberry biomass and leaf area using object-based analysis of high-resolution images. Isprs J. Photogramm 2020, 163, 171–186. [Google Scholar] [CrossRef]
- Saridas, M.A.; Simsek, O.; Donmez, D.; Kacar, Y.A.; Kargi, S.P. Genetic diversity and fruit characteristics of new superior hybrid strawberry (Fragaria× ananassa Duchesne ex Rozier) genotypes. Genet. Resour. Crop Evol. 2021, 68, 741–758. [Google Scholar] [CrossRef]
- Zheng, C.; Abd-Elrahman, A.; Whitaker, V. Remote Sensing and Machine Learning in Crop Phenotyping and Management, with an Emphasis on Applications in Strawberry Farming. Remote Sens. 2021, 13, 531. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.-P.; Yin, T.; Lauret, N.; Cajgfinger, T.; Gregoire, T.; Grau, E.; Feret, J.-B.; Lopes, M.; Guilleux, J.; Dedieu, G.; et al. Discrete Anisotropic Radiative Transfer (DART 5) for Modeling Airborne and Satellite Spectroradiometer and LIDAR Acquisitions of Natural and Urban Landscapes. Remote Sens. 2015, 7, 1667–1701. [Google Scholar] [CrossRef] [Green Version]
- Aber, J.S.; Marzolff, I.; Ries, J.B. Chapter 10—Image Interpretation. In Small-Format Aerial Photography; Aber, J.S., Marzolff, I., Ries, J.B., Eds.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 139–157. [Google Scholar]
- Nicodemus, F.E.; Richmond, J.C.; Hsia, J.J.; Ginsberg, I.W.; Limperis, T. Geometrical considerations and nomenclature for reflectance. In Radiometry; Jones and Bartlett Publishers, Inc.: Burlington, MA, USA, 1992; pp. 94–145. [Google Scholar]
- Banskota, A.; Serbin, S.P.; Wynne, R.H.; Thomas, V.A.; Falkowski, M.J.; Kayastha, N.; Gastellu-Etchegorry, J.P.; Townsend, P.A. An LUT-Based Inversion of DART Model to Estimate Forest LAI from Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3147–3160. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Gascon, F.; Estève, P. An interpolation procedure for generalizing a look-up table inversion method. Remote Sens. Env. 2003, 87, 55–71. [Google Scholar] [CrossRef]
- Kimes, D.; Gastellu-Etchegorry, J.; Estève, P. Recovery of forest canopy characteristics through inversion of a complex 3D model. Remote Sens. Env. 2002, 79, 320–328. [Google Scholar] [CrossRef]
- Yáñez-Rausell, L.; Malenovský, Z.; Rautiainen, M.; Clevers, J.G.P.W.; Lukeš, P.; Hanuš, J.; Schaepman, M.E. Estimation of Spruce Needle-Leaf Chlorophyll Content Based on DART and PARAS Canopy Reflectance Models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1534–1544. [Google Scholar] [CrossRef] [Green Version]
- Couturier, S.; Gastellu-Etchegorry, J.-P.; Patiño, P.; Martin, E. A model-based performance test for forest classifiers on remote-sensing imagery. For. Ecol. Manag. 2009, 257, 23–37. [Google Scholar] [CrossRef] [Green Version]
- Schneider, F.D.; Leiterer, R.; Morsdorf, F.; Gastellu-Etchegorry, J.-P.; Lauret, N.; Pfeifer, N.; Schaepman, M.E. Simulating imaging spectrometer data: 3D forest modeling based on LiDAR and in situ data. Remote Sens. Env. 2014, 152, 235–250. [Google Scholar] [CrossRef]
- Prusinkiewicz, P.; Karwowski, R.; Měch, R.; Hanan, J. L-studio/cpfg: A software system for modeling plants. In International Workshop on Applications of Graph Transformations with Industrial Relevance; Springer: Berlin/Heidelberg, Germany, 1999; pp. 457–464. [Google Scholar]
- Karwowski, R.; Lane, B. L-Studio 4.0 User’s Guide. Available online: http://algorithmicbotany.org/lstudio/index.html (accessed on 19 December 2021).
- Prusinkiewicz, P.; Hanan, J.; Měch, R. An L-system-based plant modeling language. In Proceedings of the International workshop on applications of graph transformations with industrial relevance, Kerkrade, The Netherlands, 1–3 September 1999; pp. 395–410. [Google Scholar]
- Paul, R.; Wolf, P.D.; Bon, A.; Dewitt, P.D.; Benjamin, E.; Wilkinson, P.D. Elements of Photogrammetry with Applications in GIS, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Agisoft, L. Agisoft PhotoScan user manual. Aplastic Anemia (Hypoplastic Anemia) 2016, 1, 37. [Google Scholar]
- Izzo, L.G.; Aronne, G. Root Tropisms: New Insights Leading the Growth Direction of the Hidden Half. Plants 2021, 10, 220. [Google Scholar] [CrossRef]
- Thimann, K.V. Chapter I-Phototropism. In Comprehensive Biochemistry; Florkin, M., Stotz, E.H., Eds.; Elsevier: Amsterdam, The Netherlands, 1967; Volume 27, pp. 1–29. [Google Scholar]
- Goudriaan, J.; Monteith, J. A mathematical function for crop growth based on light interception and leaf area expansion. Ann. Bot. 1990, 66, 695–701. [Google Scholar] [CrossRef] [Green Version]
- Monson, R.K.; Weraduwage, S.M.; Rosenkranz, M.; Schnitzler, J.-P.; Sharkey, T.D. Leaf isoprene emission as a trait that mediates the growth-defense tradeoff in the face of climate stress. Oecologia 2021, 197, 885–902. [Google Scholar] [CrossRef]
- Richards, F. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–301. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.-P. 3D modeling of satellite spectral images, radiation budget and energy budget of urban landscapes. Meteorol. Atmos. Phys. 2008, 102, 187–207. [Google Scholar] [CrossRef] [Green Version]
- Gastellu-Etchegorry, J.; Martin, E.; Gascon, F. DART: A 3D model for simulating satellite images and studying surface radiation budget. Int. J. Remote Sens. 2004, 25, 73–96. [Google Scholar] [CrossRef]
- NOAA Solar Calculator. Available online: https://www.esrl.noaa.gov/gmd/grad/solcalc/ (accessed on 28 October 2021).
- Ross, J. The Radiation Regime and Architecture of Plant Stands; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- WATSON, D.J. Comparative Physiological Studies on the Growth of Field Crops: I. Variation in Net Assimilation Rate and Leaf Area between Species and Varieties, and within and between Years. Ann. Bot. 1947, 11, 41–76. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Env. 1984, 16, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Env. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Kross, A.; McNairn, H.; Lapen, D.; Sunohara, M.; Champagne, C. Assessment of RapidEye vegetation indices for estimation of leaf area index and biomass in corn and soybean crops. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 235–248. [Google Scholar] [CrossRef] [Green Version]
- Rouse, J. Monitoring the Vernal Advancement and Retrogradation of Natural Vegetation [NASA/GSFCT Type II Report]; NASA/Goddard Space Flight Center: Greenbelt, MD, USA, 1973.
- Jordan, C.F. Derivation of leaf-area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Spectral reflectance changes associated with autumn senescence of Aesculus hippocastanum L. and Acer platanoides L. leaves. Spectral features and relation to chlorophyll estimation. J. Plant Physiol. 1994, 143, 286–292. [Google Scholar] [CrossRef]
- Chen, P.-F.; Nicolas, T.; Wang, J.-H.; Philippe, V.; Huang, W.-J.; Li, B.-G. New index for crop canopy fresh biomass estimation. Spectrosc. Spectr. Anal. 2010, 30, 512–517. [Google Scholar]
- Zeng, Y.; Hao, D.; Badgley, G.; Damm, A.; Rascher, U.; Ryu, Y.; Johnson, J.; Krieger, V.; Wu, S.; Qiu, H.; et al. Estimating near-infrared reflectance of vegetation from hyperspectral data. Remote Sens. Env. 2021, 267, 112723. [Google Scholar] [CrossRef]
- RStudio Team. RStudio: Integrated Development for R; RStudio, Inc.: Boston, MA, USA, 2015. [Google Scholar]
- O’brien, R.M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]













| No. | Band Name | Center Wavelength (nm) | Bandwidth (nm) | |
|---|---|---|---|---|
| MicaSense | 1 | Blue | 475 | 32 |
| 2 | Green | 560 | 27 | |
| 3 | Red | 668 | 14 | |
| 4 | Red Edge | 717 | 12 | |
| 5 | Near IR | 842 | 57 |
| Date | Days after Planting | B | G | R | RedEdge | NIR |
|---|---|---|---|---|---|---|
| 16/11/2017 | 31 | 0.143 | 0.145 | 0.038 | 0.199 | 0.386 |
| 21/11/2017 | 36 | 0.111 | 0.114 | 0.027 | 0.158 | 0.309 |
| 30/11/2017 | 45 | 0.129 | 0.130 | 0.032 | 0.181 | 0.357 |
| 7/12/2017 | 52 | 0.146 | 0.146 | 0.021 | 0.218 | 0.478 |
| 14/12/2017 | 59 | 0.117 | 0.119 | 0.020 | 0.172 | 0.355 |
| 21/12/2017 | 66 | 0.128 | 0.129 | 0.032 | 0.178 | 0.377 |
| 27/12/2017 | 72 | 0.138 | 0.141 | 0.019 | 0.206 | 0.440 |
| 4/1/2018 | 80 | 0.139 | 0.141 | 0.029 | 0.196 | 0.433 |
| 11/1/2018 | 87 | 0.129 | 0.130 | 0.016 | 0.195 | 0.423 |
| 18/1/2018 | 94 | 0.129 | 0.131 | 0.024 | 0.183 | 0.424 |
| 25/1/2018 | 101 | 0.133 | 0.135 | 0.013 | 0.204 | 0.455 |
| 1/2/2018 | 108 | 0.136 | 0.140 | 0.024 | 0.196 | 0.466 |
| 8/2/2018 | 115 | 0.145 | 0.147 | 0.016 | 0.219 | 0.489 |
| 15/2/2018 | 122 | 0.138 | 0.141 | 0.023 | 0.198 | 0.474 |
| 22/2/2018 | 129 | 0.112 | 0.114 | 0.020 | 0.165 | 0.337 |
| 27/2/2018 | 134 | 0.131 | 0.138 | 0.015 | 0.195 | 0.483 |
| Acronym | Index | Equation | Reference |
|---|---|---|---|
| gNDVI | Green NDVI | [50] | |
| NDVI | Normalized Difference Vegetation Index | [51] | |
| SR | Simple Ratio | [52] | |
| NDVIre | Red Edge Normalized Difference Vegetation Index | [53] | |
| SRre | Red edge Simple Ratio | [53] | |
| RTVI | Red Edge Triangular Vegetation Index | [54] | |
| NIRv | Near-infrared reflectance of vegetation | [55] |
| Leaf Size at Maturity (m) | Petiole Length at Maturity (m) | |
|---|---|---|
| Minimum | 5.00 × 10−2 | 6.00 × 10−2 |
| Maximum | 8.00 × 10−2 | 1.15 × 10−2 |
| Range | 3.80 × 10−2 | 5.50 × 10−2 |
| Mean | 7.02 × 10−2 | 9.00 × 10−2 |
| Median | 7.40 × 10−2 | 9.30 × 10−2 |
| standard deviation | 1.20 × 10−2 | 1.84 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, Z.; Abd-Elrahman, A.; Whitaker, V.; Agehara, S.; Wilkinson, B.; Gastellu-Etchegorry, J.-P.; Dewitt, B. Radiative Transfer Image Simulation Using L-System Modeled Strawberry Canopies. Remote Sens. 2022, 14, 548. https://doi.org/10.3390/rs14030548
Guan Z, Abd-Elrahman A, Whitaker V, Agehara S, Wilkinson B, Gastellu-Etchegorry J-P, Dewitt B. Radiative Transfer Image Simulation Using L-System Modeled Strawberry Canopies. Remote Sensing. 2022; 14(3):548. https://doi.org/10.3390/rs14030548
Chicago/Turabian StyleGuan, Zhen, Amr Abd-Elrahman, Vance Whitaker, Shinsuke Agehara, Benjamin Wilkinson, Jean-Philippe Gastellu-Etchegorry, and Bon Dewitt. 2022. "Radiative Transfer Image Simulation Using L-System Modeled Strawberry Canopies" Remote Sensing 14, no. 3: 548. https://doi.org/10.3390/rs14030548
APA StyleGuan, Z., Abd-Elrahman, A., Whitaker, V., Agehara, S., Wilkinson, B., Gastellu-Etchegorry, J.-P., & Dewitt, B. (2022). Radiative Transfer Image Simulation Using L-System Modeled Strawberry Canopies. Remote Sensing, 14(3), 548. https://doi.org/10.3390/rs14030548