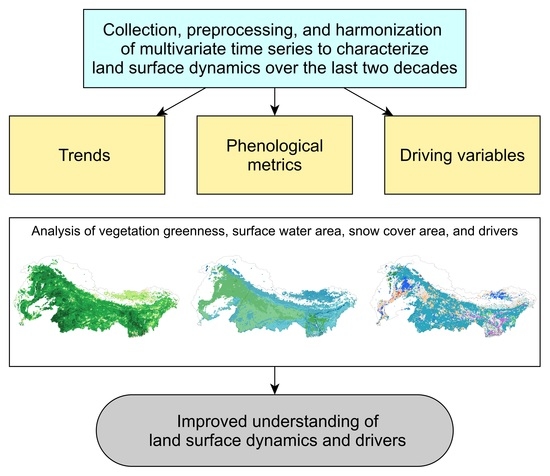
A Framework for Multivariate Analysis of Land Surface Dynamics and Driving Variables—A Case Study for Indo-Gangetic River Basins

Abstract

The analysis of the Earth system and interactions among its spheres is increasingly important to improve the understanding of global environmental change. In this regard, Earth observation (EO) is a valuable tool for monitoring of long term changes over the land surface and its features. Although investigations commonly study environmental change by means of a single EO-based land surface variable, a joint exploitation of multivariate land surface variables covering several spheres is still rarely performed. In this regard, we present a novel methodological framework for both, the automated processing of multisource time series to generate a unified multivariate feature space, as well as the application of statistical time series analysis techniques to quantify land surface change and driving variables. In particular, we unify multivariate time series over the last two decades including vegetation greenness, surface water area, snow cover area, and climatic, as well as hydrological variables. Furthermore, the statistical time series analyses include quantification of trends, changes in seasonality, and evaluation of drivers using the recently proposed causal discovery algorithm Peter and Clark Momentary Conditional Independence (PCMCI). We demonstrate the functionality of our methodological framework using Indo-Gangetic river basins in South Asia as a case study. The time series analyses reveal increasing trends in vegetation greenness being largely dependent on water availability, decreasing trends in snow cover area being mostly negatively coupled to temperature, and trends of surface water area to be spatially heterogeneous and linked to various driving variables. Overall, the obtained results highlight the value and suitability of this methodological framework with respect to global climate change research, enabling multivariate time series preparation, derivation of detailed information on significant trends and seasonality, as well as detection of causal links with minimal user intervention. This study is the first to use multivariate time series including several EO-based variables to analyze land surface dynamics over the last two decades using the causal discovery algorithm PCMCI.

1. Introduction

Amplified global climate change results in modified climate variability and severely impacts land surface processes worldwide [1]. Accordingly, a continuous monitoring of these transformation processes is required to quantify and understand their characteristics, drivers, and impacts [2]. In this context, time series analysis tools are crucial to identify spatio-temporal patterns and examine changes over time [3]. In terms of continuous monitoring of the land surface, Earth observation (EO) provides increasing amounts of data streams over the entire globe for already decades [4,5]. In addition to raw EO data, many subsequently generated geospatial data products, so-called analysis ready data (ARD) that characterize the global land surface are available. These include geophysical variables, such as land surface temperature, net primary productivity, or albedo (e.g., [6,7,8]), index variables such as the normalized difference vegetation index (NDVI) or the leaf area index (LAI) (e.g., [9,10]), and thematic variables representing, e.g., forest cover, surface water area, snow cover area, and settlement area (e.g., [11,12,13,14,15,16,17]). The large availability of EO and further geoscientific time series enables the joint exploration of interactions among various spheres of the Earth system at global scale and have the potential to enhance our understanding of environmental change considerably [18,19,20]. However, the investigation of multivariate time series including several EO-based land surface variables in combination with climatic, hydrological, and anthropogenic variables remains underexploited and is hampered by varying data characteristics in terms of spatial and temporal resolution as well as processing and storage capacities.

To exploit the full potential of multivariate time series, methodological frameworks integrating both the preparation of multisource geospatial time series and the application of respective statistical analysis tools are necessary. In this connection, Sudmanns et al. [21] provides an overview of selected architectures and data portals allowing the access to and the analysis of large amounts of EO data, particularly ARD, with the Google Earth Engine [22] being probably the most prominent example. A further solution to store, organize, and analyze EO data is the data cube environment [21,23,24]. In this regard, there is a variety of operational data cubes at regional scale using the Open Data Cube framework [25,26,27,28,29,30]. Recent progress in data cubes and multivariate analysis methods point towards the importance of joint analyses of time series rather than a single variable [18,31]. In agreement with these developments, the aim of this study is to implement a simplified methodological framework for both preparation and statistical analysis of multivariate time series. Compared to other approaches, we envision an easy-to-implement and flexible framework with respect to the unification of multisource data streams. In particular, this applies to the spatial and temporal resolution, which should ideally be adjustable to any grid space or geographical entity and temporal intervals, respectively.

In the context of statistical time series analysis with respect to land surface dynamics, studies often investigate time series on a single EO-based land surface variable, such as the vegetation index to calculate change over time. This univariate domain measures one variable and includes techniques, such as trend estimation (e.g., [32,33,34,35]), changepoint detection (e.g., [36,37]), and calculation of phenological metrics (e.g., [38,39,40]). On the other hand, fewer studies investigate the influence of driving variables using multivariate time series. Multivariate time series analyses aim at quantifying the relation between two or more variables, as well as at exploring interdependencies between several features. For this purpose, past studies used methods including traditional correlative approaches between two variables (e.g., [41,42,43]) or partial correlation analyses using one or more controlling variables (e.g., [44,45]). Recently, studies investigating causal inference from empirical data provided important insights and directions on the application of causal discovery approaches [46,47,48]. The application of such causal discovery algorithms aims at reducing potential spurious links, which could appear in traditional correlation approaches, and include advanced analysis of interactions in a high dimensional feature space. Specifically, Runge [49] introduced an approach called Peter and Clark Momentary Conditional Independence (PCMCI) to construct causal networks. Here, a causal network describes and quantifies the relation between variables at different time steps in the past. PCMCI constructs causal networks to analyze relationships between several features at past time lags while being capable of dealing with a high dimensional feature space and highly autocorrelated variables [49]. However, up to date, a detailed application and evaluation of causal networks with PCMCI for multivariate time series covering EO-based land surface variables remains limited [50].

In order to address the lack of multivariate remote sensing time series analyses across spheres, we present a novel methodological framework allowing the large scale processing of multisource geospatial time series and demonstrate its potential to characterize land surface dynamics for a case study in South Asia over the last two decades. Accordingly, the objectives of this study are to: (1) implement a framework being transferable in space and time and aiming at preparing and unifying multivariate time series and (2) enable quantitative analyses of land surface dynamics through derivation of trends, changes in seasonality, as well as evaluation of driving variables using PCMCI. For the first time, we jointly analyze land surface variables including EO time series on vegetation greenness, surface water area, and snow cover area in combination with climatic and hydrological variables over two decades. In the following, Section 2 presents the study area. Next, Section 3 describes the used time series, as well as the implemented methodological framework for time series preprocessing, generation of the unified database, and the employed statistical time series analysis techniques. Following this, Section 4 presents the results of the statistical analyses and Section 5 discusses the results, remaining limitations, and future requirements. Ultimately, Section 6 summarizes the findings of this paper.

2. Study Area

Our framework is demonstrated using the Indus-Ganges-Brahmaputra-Meghna river basins (IGBMRB) in South Asia as a case study (Figure 1). These river basins stretch over Pakistan, India, China, Nepal, Bhutan, and Bangladesh covering an area of approximately 2.9 million km${}^2$ [51]. The northern regions of the river basins are marked by the Himalaya mountains being dominated by cold and polar climate in high elevation. South of the high altitude areas, the Himalaya is characterized by forest vegetation and temperate as well subtropical climate, whereas the low altitude areas in the Indo-Gangetic plain are marked by intensive agricultural and highly urbanized land use (Figure 1B). Here, the climate is arid in the West as well as temperate and tropical in the South and East of the study area, respectively (Figure 1C). Moreover, moist southwest monsoon causing high rainfall is dominating the climate between June and September, while dry northeast monsoon winds prevail during the winter months between December and February.

3. Materials and Methods

Our methodological framework focuses on the analysis of land surface dynamics by means of multivariate geospatial time series. First, the gathered time series data are introduced. Next, our approach to generate a unified feature space is presented and, lastly, the implemented statistical time series analysis techniques are described. At this point it has to be noted that all implemented processing steps ranging from preprocessing over database generation to statistical time series analyses can be run automatically with a global set of parameters. A brief summary of our implemented framework is presented in Figure 2.

3.1. Data

3.1.1. MODIS NDVI

To assess vegetation dynamics, we employed the global MODIS NDVI product (MOD13C2.006) at 0.05${}^{\circ }$ spatial resolution and monthly temporal resolution covering the years 2000 to 2019 [9]. This cloud-free product is based on spatial and temporal averages of high quality MODIS 16-day 1 km NDVI. The preprocessing of these data includes the exclusion of all pixels flagged “mixed cloud”, “adjacent cloud”, and “possible shadow” in the quality assurance layer and the filling of gaps using linear interpolation [34]. Next, we remove NDVI pixels labeled as “snow” in the reliability layer of the respective time step. Finally, to exclude non-vegetated areas all NDVI pixels with a long-term mean lower than 0.15 are masked, as suggested in Wittich and Hansing [56].

3.1.2. Global Snowpack (GSP)

GSP is processed at the German Remote Sensing Data Center of the German Aerospace Center (DLR-DFD) using daily MODIS products (M*D10A1.006) at 500 m pixel resolution [14]. This daily time series represents snow cover area as a binary mask with pixels classified as “snow” and “no-snow”. GSP data were already employed in several studies to investigate snow cover phenology [57,58,59]. Details on validation of MODIS snow products are provided in Dietz et al. [14] and Notarnicola [42]. To reduce uncertainties and ephemeral snow, we calculate a long-term mean at pixel scale and remove pixels with a fractional snow cover lower than 10%. Additionally, snow patches with less than 10 pixels are filtered as suggested by Notarnicola [42] and water bodies are excluded using the European Space Agency (ESA) Climate Change Initiative (CCI) land cover product [60]. Furthermore, to minimize uncertainties in low altitudes caused by clouds during the monsoon season, we exclude pixels at an elevation lower than 1500 m and being located in temperate or tropical zones. For this purpose, the Copernicus Digital Elevation Model (DEM) with 90 m resolution [52] and climate classification data from Beck et al. [61] were used. Finally, we aggregated daily GSP to monthly mean composites covering the period between 2000 and 2019.

3.1.3. Global Waterpack (GWP)

Surface water area dynamics are represented by GWP being produced at DLR-DFD at a spatial resolution of 250 m and a daily temporal resolution using global MODIS imagery (M*DGQ09.006) [13,38]. This dataset characterizes surface water area as a binary mask with pixels classified as “water” and “no-water”. For details on data processing and validation, the reader is referred to Klein et al. [13]. After mosaicking and reprojecting the GWP tiles, we aggregate daily GWP to monthly composites. In contrast to NDVI and GSP, GWP is available between 2003 and 2019 only as it relies on the combination of both Terra and Aqua sensor data.

3.1.4. Climatological and Hydrological Data

Furthermore, climatic and hydrological variables were assembled to estimate their influence on land surface parameters. We selected these time series based on the relevance as a driving variable with respect to the land surface variables, their availability over the last two decades, and their spatial and temporal resolution. In particular, we use the Climate Hazards Group Infrared Precipitation with Station data (CHIRPS) v2.0 being a blend of station measurements, satellite acquisitions, and long-term climatology to characterize precipitation at monthly scale [54]. This product has a spatial resolution of 0.05${}^{\circ }$ (5 km) and shows good performance in capturing precipitation patterns over India [62,63]. Moreover, we calculate monthly mean air temperature based on minimum and maximum air temperature from the TerraClimate dataset at a spatial resolution of 1/24${}^{\circ }$ (4 km) [55]. From TerraClimate, we also embed downward shortwave radiation and vapor pressure deficit (VPD). TerraClimate data are widely used (e.g., [64,65]) and accuracy measures are available in Abatzoglou et al. [55]. Next, to analyze surface water dynamics, we incorporate the Global Flood Awareness System (GloFAS)-ERA5 river discharge data at a spatial resolution of 0.1${}^{\circ }$ (10 km) [66]. Despite the fact that the gridded river discharge data have not been extensively validated over the investigated river basins, Harrigan et al. [66] reported good performance compared with globally distributed observations. In addition, we include soil moisture from the Global Land Evaporation Amsterdam Model (GLEAM v3.5a) at a spatial resolution of 0.25${}^{\circ }$ (25 km) [67,68]. These data cover the period between 2000 and 2019.

3.2. Database Generation

Since all time series come with different characteristics, the generation of a unified feature space in terms of spatial and temporal resolution is required, in order to enable joint analyses with multisource variables (Figure 3). In this study, the multivariate time series are unified by means of grid cells covering our study area at a spatial resolution of 0.1${}^{\circ }$ (approximately 10 km). During this process, all time series are aggregated to the uniform grid at monthly temporal resolution. Spatial aggregation is performed by averaging pixels intersecting a given grid cell, weighted by the fraction of the pixel that is covered by the grid cell. Likewise, the spatial and temporal aggregation is applicable to any other geographical entity and temporal intervals, respectively. We implement our framework using R and Python programming language. In particular, we employ, i.e., the exact extract library (https://github.com/isciences/exactextract/; accessed on 10 November 2021) for spatial aggregation of all variables. The preprocessing and spatial aggregation of the geospatial time series is conducted on a high performance cluster using docker containers with minimum user interaction. The unified feature space is represented by dataframes, including the respective time series variables for each grid cell. These dataframes are used as input for the following time series analyses methods (Figure 3).

3.3. Time Series Analyses

In the following, the statistical time series analysis methods and global parameter settings implemented in our framework are introduced. In order to measure change over time, monotonic trends of the land surface variables NDVI, GWP, and GSP are analyzed. Specifically, we quantify the significance of trends and the magnitude of change per unit time. Since the variables are characterized by clear seasonal cycles, we use the non-parametric seasonal Mann–Kendall (MK) test [69] in association with the Theil–Sen (TS) slope estimator [70,71]. For this purpose, we split the time series keeping the monthly resolution into the following seasons: winter (December, January, February; “DJF”), pre-monsoon (March, April, May; “MAM”), monsoon (June, July, August, September; “JJAS”), and post-monsoon season (October, November; “ON”) [72]. Figure 4 illustrates details on the implemented workflow related to trend tests. Throughout this study, trends are considered as significant at a confidence level of 95% (p-value < 0.05). Trends with a p-value above this threshold are treated as no change. As for seasonal MK test, the TS slope is first determined for each season. The global slope value is calculated based on the median of the seasonal slopes and only assigned if these are homogenous at a confidence level of 90% [73]. In order to quantify the magnitude of the slope at decadal time scale, the obtained global slope is multiplied with the number of years per decade.

3.3.1. Trend Tests

Furthermore, both statistical measures have no requirement for data distribution, but expect the time series to be serially independent. Approaches to account for serial correlation include aggregation of time series to annual scale or pre-whitening (PW). However, temporal aggregation to annual resolution reduces the number of data points and consequently yields smaller statistical significance [73]. Thus, to reduce seasonal influence and serial correlation, seasonal anomalies are derived by calculating the departure of the actual monthly observation from the long term mean of the respective month (Figure 5). Afterwards, we check the existence of lag-1 autocorrelation ($r_1$). If $r_1$ is not significant, MK test and TS slope estimator are applied on the seasons of the anomalized time series. If $r_1$ is significant, the time series is pre-whitened to reduce autocorrelation. In general, PW removes the lag-1 autocorrelation from the time series. Depending on the selected PW approach, it can result in high or low type I error and biased slope estimates. Findings in literature indicate that trend-free pre-whitening after Yue et al. [74] (TFPW-Y) has a high test power and is the most frequently applied PW algorithm [73]. TFPW-Y blends the time series by removing $r_1$ coefficient from it. However, studies show that application of TFPW-Y might cause high type I error and an overestimated slope estimate [73,75]. In this regard, studies suggest not to rely on only one PW algorithm [75]. Hence, we additionally use the trend-free pre-whitening approach after Wang and Swail [76] (TFPW-WS) being characterized by a low type I error and high test power. TFPW-WS removes serial correlation in an iterative procedure while preserving the trend. Furthermore, to account for biased slope values through PW, Collaud Coen et al. [73] recommend to apply the TS slope estimator on a time series pre-whitened with a variance correction procedure (VCPW) after Wang et al. [75]. As depicted in Figure 4 we apply one setting including the TFPW-Y approach for both MK test and slope estimation and a further setting using TFPW-WS and VCPW to assess significance of trend and derive an unbiased slope estimate, respectively.

3.3.2. Seasonality Analysis

In addition to trends, phenological metrics are derived to evaluate changes in seasonal characteristics. For this purpose, the Timesat tool (version 3.3) is used in this framework [77,78]. Timesat is commonly applied in the context of seasonal analysis of water or vegetation parameters [38,39,79] and is here employed to derive phenological metrics for NDVI, GWP, and GSP. In detail, we determine the metrics seasonal amplitude, timing of seasonal peaks, value of seasonal peak, and duration of season. With respect to Timesat, we use the seasonal amplitude setting with a 50% fraction of the amplitude to retrieve the start and end of the season [38]. Since the time series are already interpolated and smoothed by means of temporal and spatial aggregation during preprocessing and database generation, additional smoothing is not performed using Timesat. This avoids a further loss of information and modification of the generated monthly time series. Moreover, within this framework we assume one annual season for all variables. Only for NDVI, a second setting is implemented to additionally consider areas characterized by two annual growing seasons. Furthermore, for derivation of phenological metrics for GWP and GSP, the hydrological year starting in June and ending in May is considered [80]. The retrieved seasonal properties are utilized to calculate changes in the phenological metrics by splitting the time series into two decades (2000–2009 and 2010–2019). To this end, the derived seasonal properties are averaged per decade and then the difference of both decades is determined by using the respective mean seasonal peak and seasonal duration at monthly scale.

3.3.3. Causal Discovery Algorithm

The implemented framework includes a further step to exploit the multivariate feature space by means of the causal discovery algorithm PCMCI. This step enables the analysis of drivers for the land surface variables NDVI, GWP, and GSP, in the following denoted as targets. The driving variables were introduced in Section 3.1.4. In the context of PCMCI, drivers are also called parents. To explore the causal network structure of the underlying feature space, we use the PCMCI approach with the ParCorr linear independence test based on partial correlation [48,49].

In general, PCMCI is capable of eliminating spurious links and, thus, assessing true causal links for a defined set of temporal lags ($\tau$) [49]. As pointed out by Runge [49], several assumptions need to be considered when conducting causal interpretation. In this study, we assume the detected causal links to be relative with respect to the feature space, meaning that the causal network might differ when changing the feature space. Furthermore, stationarity in time series is an important requirement of PCMCI when employing partial correlation as independence test [48]. To meet this requirement to account for an important requirement of PCMCI when adopting partial correlation as independence test is stationarity in time series [47]. For this purpose, we remove the linear trend by least square fit and calculate seasonal anomalies (Figure 5). Afterwards, all univariate detrended anomaly time series are processed by a two-step approach within the PCMCI framework, including the modified Peter and Clark (PC1), as well as the momentary conditional independence (MCI) algorithm [49] being available in the Python package tigramite (https://github.com/jakobrunge/tigramite/; accessed on: 10 November 2021).

With more detail, the first step consists of condition selection using PC1. As an example, when GSP is our target variable $X_t^j$, we include further variables $X_t^i$ as potential parents with i being the variable index and t the time index, i.e., $i\in \left\{T,P,DSR\right\}$, and $t\in \left\{1,...,{\tau }_{max}\right\}$, respectively. If during PC1 step any lagged variable is found to be significantly influencing a target variable, it is considered in the set of parents $\tilde{P}\left(X_t^j\right)$. According to the defined significance level (${\alpha }_{pc}$), a potential parent might be classified as irrelevant. In the second step, MCI uses all identified lagged parents together with contemporaneous (lag 0) pairs accounting for common drivers, indirect links, and autocorrelation [48]. Moreover, in this study MCI quantifies the strength of a causal link using partial correlation and the statistical significance based on a two-sided t-test. For a detailed description of the theory behind PCMCI, the reader is referred to Runge et al. [48], Runge [49], and Krich et al. [50].

To set up PCMCI for this framework, the global settings listed in

Table 1. Summary of selected settings for PCMCI. For further details the reader is referred to Runge et al. [48] and Runge [49].

Parameter	Description	Used Value
Dataframe	Includes time series variables and temporal information. If data mask is used, it is appended to the data frame.	Targets and drivers
Data mask	Mask defining time steps to include and exclude (0: False, 1: True).	Seasons
Mask type	Definition of which variables and time steps to mask, e.g., type “y” masks target variable as defined in mask, but allows drivers depending on temporal lags to be outside of mask.	“y”
Lags	Temporal lags to test (minimum, maximum).	min: 0, max: 3
Independence test	Conditional independence test including linear (e.g., partial correlation) and non-linear dependencies.	“ParCorr”
${\alpha }_{pc}$	Significance threshold in condition selection step (PC1), comparable to hyperparameter optimization in model selection process. If “None” is used, optimal value is selected via Akaike information criterion score.	“None”
$\alpha$	Threshold to extract significant links detected for each target variable in MCI test.	0.05
Selected links	Definition of potential causal links to be tested. A detailed specification of, i.e., a target variable, potential parents, and maximum lags is possible. We only consider parents for the three target variables.	$X_{t-\tau }^i\to X_t^j$
False discovery rate	Parameter to account for inflated p-value due to multiple testing in MCI step.	“fdr_bh”

are used. First, we define a maximum time lag of 3 months for causal network generation. Causal links are detected based on lagged dependencies, while contemporaneous links are usually left undirected. Since we only calculate parents for the target variables NDVI, GWP, and GSP, we can use the direction of influence also for contemporaneous links. Furthermore, the mask option is employed to all target variables to construct the causal networks at a defined temporal scale. Considering NDVI, the time series are limited to the growing season by excluding all NDVI values lower than 0.2 and temperature lower than 0, as suggested by Wu et al. [45]. Similarly, for GWP and GSP, time steps with a minimum surface water and snow cover extent below a threshold of 0.5% are excluded. Here, masking only limits the target variable, whereas the lagged drivers also include data points of masked time steps in the past. In addition, we correct the derived p-values from MCI to control the number of false positive discoveries due to multiple testing [49].

4. Results

4.1. Trends

As illustrated in Figure 6, the design of the trend test’s results in a different amount of statistically significant trends for each setting (Figure 4). To account for serial correlation, we applied TFPW-Y and TFPW-WS in association with VCPW. The results indicate that for 100.0%, 99.8%, and 99.8% of all grids, lag-1 autocorrelation is significant for NDVI, GWP, and GSP, respectively. In addition,

Table 2. Comparison of significant trends and their direction (pos.: positive, neg.: negative) derived with different PW algorithms. The results of the seasonal MK test are listed as percentages for NDVI, GWP, and GSP and include each season and trends at annual scale (NH: not homogeneous, NS: not significant).

Variable	Sum of Grids	Setting	DJF		MAM		JJAS		ON		Annual
			Pos.	Neg.	Pos.	Neg.	Pos.	Neg.	Pos.	Neg.	Pos.	Neg.	NH	NS
NDVI	19,333	NOPW	81.1	1.1	73.5	0.9	79.8	1.4	81.7	0.8	91.0	0.9	1.1	7.0
		TFPW-Y	92.2	1.5	86.9	1.4	90.8	1.1	84.7	1.1	94.3	1.5	0.7	3.5
		TFPW-WS	52.6	3.9	26.1	23.6	47.3	2.0	20.0	19.5	23.3	0.1	48.8	27.8
GWP	3395	NOPW	28.5	19.4	29.1	15.9	22.0	27.1	26.5	23.3	32.6	27.0	11.2	29.2
		TFPW-Y	29.7	21.8	32.7	25.3	28.0	29.0	31.3	22.1	38.6	32.7	9.5	19.2
		TFPW-WS	17.1	15.6	17.8	11.5	12.5	21.9	20.9	17.0	12.0	9.6	28.7	49.7
GSP	6364	NOPW	0.6	5.5	14.2	4.5	11.3	6.2	1.5	7.0	15.8	13.1	0.6	70.5
		TFPW-Y	0.6	3.0	18.6	4.3	5.6	11.0	3.0	8.8	18.3	16.7	0.7	64.3
		TFPW-WS	0.5	4.8	10.6	4.5	3.7	5.9	1.5	6.2	1.9	7.1	7.1	83.9

demonstrates that trends identified over the seasons and aggregated to annual scale are more frequently heterogeneous when using VCPW. On the contrary, the usage of TFPW-Y yields more significant trends than TFPW-WS and more homogeneous trends than VCPW for almost all land surface variables. Additionally, it becomes evident that the application of no PW algorithm yields similar percentages for positive and negative trends as TFPW-Y, with TFPW-Y indicating mostly higher percentages. Considering the magnitude of significant trends derived with TFPW-Y and VCPW, Figure 6G shows that the usage of VCPW results in lower absolute slope values. In particular, the mean absolute slope with NOPW, TFPW-Y, and VCPW amounts to 0.034, 0.034, and 0.014; 1.885, 1.690, and 0.873; as well as 2.815, 2.615, and 1.658 for NDVI, GWP, and GSP, respectively.

In terms of spatial distribution, significant NDVI trends at annual scale indicate widespread increases in vegetation greenness almost over the entire study area (Figure 6). These trends are most pronounced in the southwest of the Ganges river basin and less over high altitudes and the foothills of the Himalayan mountain range in the Brahmaputra river basin. Moreover, trend analysis of GWP data results in heterogeneous patterns of significant positive and negative trends for surface water area. Strong significant positive trends occur, e.g., in the south of the Ganges river basin. TFPW-Y indicates strong significant negative trends particularly at the conjunctions of the rivers Ganges, Brahmaputra, and Meghna. Mixed patterns of significant positive and negative trends occur at the Brahmaputra river downstream the Himalaya mountains. Additionally, trends derived with GSP data demonstrate a two-fold pattern at annual scale. In particular, significant positive trends appear in the Upper Indus river basin, whereas significant negative trends prevail within the Upper Ganges and Brahmaputra river basins.

4.2. Seasonal Characteristics

In light of phenological metrics, our framework used a global setting for all land surface variables and for NDVI also a second one to capture two growing seasons. In this respect, Figure 7A shows timing of peaks for NDVI during the first decade. Here, our analysis reveals that 52.3% and 47.7% of the vegetated areas are characterized by one and two annual growing seasons, respectively. Timing of peaks is found to largely occur between September and October for areas with one annual growing season, while areas with two growing seasons have their first seasonal peak in February or March and second peak in September or October. In high altitudes, the seasonal peak is reached in August. As illustrated in Figure 7D, a forward and backward shift of the timing for areas with one growing season is detected in 13.5% and 11.5% of the grids, respectively. In addition, areas with two growing seasons indicate a forward and backward shift of the timing for 19.8% and 7.9% during the first season and 10.5% and 14.1% during the second season, respectively. Furthermore, the duration of season mostly ranges between five and eight months and four months for high altitude areas (Figure 8A). Regions with two growing seasons indicate a duration of two to four months for each growing season. Differences between the two decades in duration are positive in 24.8% and negative in 17.3% of the grids (Figure 8D). In comparison, grids characterized by two growing seasons show a similar relative distribution of positive and negative changes in duration for both seasons. Considering differences in the amplitude for areas with two growing seasons, the results show a higher percentage of negative changes during the first season (26.7%) compared to the second season (19.4%). However, these variations are not reflected in the differences in the value of seasonal peak where negative changes are much lower with 9.4% and 6.5%, respectively (Figure 9A,D).

Moreover, for GWP, we found that timing of peak mostly occurs between February and April in the northern and Central Indus river basin, while in GBM river basins peaks are mostly reached between August and October (Figure 7B). Spatially, the patterns of positive and negative differences between both decades are found to be heterogeneous. In this context, positive shifts (43.2%) in the timing outweigh negative shifts (26.0%). Next, duration is greatest in high altitudes and along river streams in the central Indus river basin (greater than seven months). In most of the grids, duration lasts between three and seven months. Considering the entire study area, changes in duration are also heterogeneous. As an example, a cluster indicating increases in duration is found in the wetlands of the Meghna river basin south of the Meghalayan mountains. Furthermore, the parameters amplitude and peak value show matching spatial patterns (Figure 9B,E). The percentage of increases (positive changes) in the amplitude amount to 46.9% and are slightly lower than those of the peak value (50.4%) and, in comparison, decreases (negative changes) in the amplitude are with 52.9% more frequent than of the peak value (49.2%).

Regarding GSP, the timing of seasonal peak values indicate that 83.3% of the grids reach the maximum snow cover extent in February or March. In addition, 14.5% of the grids have a maximum in April. The latter mostly occurs in eastern regions of the Brahmaputra river basin. In contrast, in western regions of the Indus river basin the peak is reached in February. Differences between the two decades show that negative changes prevail in the east and positive changes in the west (Figure 7F). In comparison, Figure 8F demonstrates that similar patterns are present in differences of the duration. In particular, a cluster of increasing duration in the second decade is prominent in the Upper Indus river basin. However, decreases in the duration appear in 33% of the grids and outweigh the increases (29.4%). We also found changes in amplitude and peak value show similar spatial patterns over the study area, indicating that decreases in the amplitude are accompanied by decreases in peak values (Figure 9C,F).

4.3. Relation with Climatic and Hydrological Drivers

In our framework, we quantify the importance of driving variables on NDVI, GWP, and GSP using PCMCI. Here, we have to note that the target variables might also be influenced by anthropogenic influences not being covered within this study. In this study, for NDVI, we investigate the drivers precipitation, soil moisture, GWP, VPD, temperature, and radiation, while the feature space for GWP and GSP includes precipitation, GSP, river discharge, and temperature, as well as precipitation, temperature, and radiation, respectively. The results are illustrated in Figure 10 showing the maximum MCI value per grid reached by one of the drivers and the corresponding temporal lag. In addition, we depict the relation between the target and each of the driving variables being controlled by all respective driving variables in the Supplementary Figure S1.

As visualized in Figure 10A,D, the results reveal spatially varying relations between NDVI and driving variables. According to the used settings and feature space, we found that in 49.6% of the grids, NDVI is mostly positively coupled to soil moisture. The dominant temporal lag amounts to 1 month. Furthermore, in the western regions of the study area, with climate being arid, NDVI shows a high response to precipitation at a time lag of 0 and 1. In fact, the impact of precipitation on NDVI is strongest in 6.0% of the grids. Additionally, radiation has a comparatively large effect on NDVI, mostly in the Ganges river basin (10.8%). Here, the temporal lag is mostly at 0 (6.7%). At the same time, when NDVI reacts negatively to radiation, it mostly shows a positive response to precipitation (Figure S1). Moreover, in the east of the study area, VPD tends to have a high influence on NDVI with lag 1 being dominant. NDVI largely responds negatively to VPD. In addition, along the large river streams and confluences towards the delta region, PCMCI detects a high importance of GWP with respect to NDVI at lag 1. Considering high altitude areas in the northeast of the study area, precipitation and soil moisture appear to be the strongest drivers at lag 0 and 1. It has to be noted, that for 26.0% of the grids no significant link is identified.

For GWP, the results reveal that in high altitudes 12.9% of the grids respond negatively to GSP at lag 0 (Figure 10B,E). In addition, grids located in high altitudes also show GWP reacting positively to temperature, mostly at lag 0 and 1. In contrast, we found that GWP responds negatively to temperature in the lower river basins, but only for a small fraction of the grids (2.2%). As expected, discharge and precipitation are the strongest drivers of GWP in the lower river basins. Specifically, 20.0% and 7.4% of the grids indicate a positive relation between GWP and discharge, as well as GWP and precipitation. Relating to GWP, we could not derive significant links for 53.5% of the grids.

Next, as illustrated in Figure 10C,F, PCMCI indicates that GSP is significantly negatively influenced by temperature. This negative dependency is dominant at lag 0 for 46.1% of the grids. Only 5.6% of the grids indicate a negative relation between GSP and temperature at lag 1. Furthermore, in areas where the influence of precipitation on GSP is strongest, we identified a temporal lag of 0 being prominent. In terms of spatial distribution, precipitation has highest impact on GSP in the western parts of the study area. In addition, the results reveal a negative response of GSP to radiation mostly located in the Upper Indus river basin. For GSP, PCMCI results indicate no causal link for 27.1% of the grids.

5. Discussion

5.1. Trends and Seasonality

In this study, we present a novel framework for both preparation and analysis of multivariate time series. First, monotonic trends and changes in phenological metrics are assessed for vegetation greenness, surface water area, and snow cover area. The results suggest that the design of the MK test and the TS slope estimator are of high importance with respect to the amount of the detected significant trends and the magnitude of slope values. Furthermore, it is important to consider serial correlation of the time series. In this context, PW algorithms are frequently applied to minimize lag-1 autocorrelation [44,81,82,83,84]. Since the choice of a respective PW algorithm may strongly impact the results it is important to consider advantages and disadvantages of PW methods, as summarized by Collaud Coen et al. [73]. Accordingly, several studies assessed the power of trend tests, amount of type I errors, and slope biases of various PW algorithms concluding that there is no single PW algorithm meeting all criteria satisfactory [75]. As visualized in Figure 6 and Table 2, the application of TFPW-Y yields much more statistically significant trends than, e.g., TFPW-WS. Additionally, the retrieved mean absolute slope values are higher for TFPW-Y than for VCPW and are highest without application of a PW algorithm prior to trend slope estimation. In fact, high serial correlation leads to inflated slope values and additionally increases the probability of type I errors [85]. Wang et al. [75] suggest to employ multiple PW methods and consider trends as significant when there is a high agreement between different methods. Similarly, Patakamuri et al. [86] utilized five PW algorithms and considered a result as a trend, if at least three were significant.

Given the spatial distribution of detected significant trends and their direction, our results are consistent with the available literature. However, a direct comparison between studies remains challenging due to variations in data sources and preprocessing, study period, design of trend test, or used significance level. To name a few studies, Zhu et al. [87] investigated vegetation condition using LAI and identified greening trends for IGBMRB covering the period 1982 to 2009. In addition, Chen et al. [33] used LAI data between 2000 and 2017 and reported strong positive trends for the river basins covered in our study. Trend estimation based on NDVI (1982–2012) also resulted in positive slope values [88]. Considering trends of surface water area, the results partially indicate heterogeneous patterns of positive and negative slopes along the Brahmaputra river south of the Himalaya. These might be caused by the highly meandering river streams. Further on, patches of significant positive trends in southern regions of the Ganges basin can be explained by dam constructions. In consideration of snow cover extent, Notarnicola [42] used MODIS snow data (2000–2018) to quantify trends using MK test based on annually and seasonally aggregated intervals. A visual comparison with our results indicates similar directions of trends in the northwest and northeast of our study area.

Furthermore, we analyzed seasonality of land surface variables. As can be seen from Figure 6, Figure 7, Figure 8 and Figure 9, the spatial patterns of positive and negative significant trends are generally matching change analyses based on phenological metrics. Regarding the analysis of phenological metrics, studies note the difficulty in quantifying one and two growing seasons at the same time with an approach being globally transferable [38,89]. In view of NDVI, we addressed this issue by simply using two models, one tailored to one (growing) season and another to two (growing) seasons. A comparison of our results (Figure 7A) with a regional land use classification differentiating between single and double crops in the Indo-Gangetic plain, reveals the spatial agreement in distinguishing one and two growing seasons [90]. Apart from that, Cheng et al. [91] retrieved phenological metrics over the Tibetan Plateau. Here, the duration of the growing season of NDVI is between three to five months for the Upper Brahmaputra basin being consistent with our results. In light of phenological metrics derived for GWP, we found an agreement between peaks in river discharge occurring between July and August for the outlets of the Indus, Ganges, and Brahmaputra rivers [92]. However, there is a disagreement in our results covering the central Indus river, where the timing of the seasonal peak is determined mostly around April (Figure 7B). Regarding seasonality of GSP, our results show similar directions with literature. Notarnicola [42] analyzed trends in snow cover duration (2000–2018) and found significant decreasing trends in eastern regions and non-significant increasing trends in western regions of IGBMRB (Figure 8C). Similar findings are also reported by Wang et al. [93].

5.2. Analysis of Causal Links

The use of a multivariate time series has the potential to enhance causal interpretation. On the other hand, the inclusion of irrelevant variables could not only increase the dimensionality but might also decrease the detection of true causal links [48]. This issue is mitigated in PCMCI through the application of a two-step procedure, where the PC step excludes irrelevant variables and the MCI step controls highly independent variables using a conditional independence test [48]. It is also important, to mention that causal interpretation depends on several assumptions, including causal sufficiency, causal stationarity, and in case of partial correlation as conditional independence test also stationarity in time series [49]. To achieve stationarity in time series, we detrended and anomalized the time series. However, these procedures do not always guarantee elimination of non-stationarities and thus, possibly lead to violation of the assumption. Stationarity in time series can also be improved taking causal stationarity into account. This assumption implicates consideration of time steps, i.e., belonging to a meteorological or growing season [49]. Furthermore, causal sufficiency expects that all common drivers are included in the feature space and might be regarded as the most important assumption considering causal interpretations [48]. Therefore, the design of causal network analysis needs careful consideration during composition of the feature space. In this study, we primarily focus on the influence of climatic and hydrological variables, being aware that anthropogenic influences might have a great influence as well. However, causal sufficiency might not be solely depending on the feature space, but also on the temporal resolution of the variables. In particular, a too coarse temporal granularity in time series might induce disappearing causal links [49].

This study restricts the analysis of causal networks to driving variables having largest MCI effect size per grid (Figure 10). Reviewing studies dealing with relationships between land surface and climatic variables, we only identified one using PCMCI to quantify the influence of precipitation, temperature, and radiation on NDVI at large spatial scale [50]. In detail, the authors used a grid size of 0.5${}^{\circ }$ at global scale and a different feature space, which is why a direct comparison is not adequate. However, the spatial pattern of influencing variables and behavior between target and the driving variables are comparable (Figure S1). For example, our feature space and settings capture the same opposite behavior of precipitation and radiation. Furthermore, the authors also found water availability being the most important driver in high altitudes of IGBMRB at lags 0 and 1 [50]. In addition to PCMCI, there are also investigations using Granger causality framework or regression to estimate lagged dependencies of NDVI [45,46,94]. In light of GWP, river discharge strongly influences surface water area (Figure S1). However, it has to be considered that discharge is most likely positively coupled to precipitation and GSP and might not always be linearly coupled to surface water area. In detail, snowmelt and rainfall largely contribute to discharge in our study area [92], which is why the detected causal link $Q\stackrel{+}{\to }GWP$ might be a result of the indirect path $P\stackrel{+}{\to }Q\stackrel{+}{\to }GWP$ or $GSP\stackrel{+}{\to }Q\stackrel{+}{\to }GWP$. Further on, PCMCI indicates that temperature is negatively impacting snow cover in the Himalayan mountains. Huang et al. [95] analyze changes in snow cover over the entire Tibetan Plateau and also identified a negative coupling of temperature and snow cover. In detail, we identified an instantaneous impact of temperature on snow cover at lag 0 (Figure S1). The driving variables precipitation and radiation again show an adverse relation, where precipitation is positively influencing GSP over the northern Indus and Ganges river basin, radiation shows a negative effect.

5.3. Limitations and Future Requirements

In general, the developed framework demonstrates good functionality over large river basins in South Asia highlighting its potential for transferability to any other study area and time series data. For our case study, we used NDVI, GWP, and GSP derived from MODIS sensors in combination with climate variables to investigate land surface dynamics and driving variables. In this context, the temporal and spatial resolution of the land surface variables are defined by the characteristics of MODIS sensors. In particular, the analysis of inland water bodies based on GWP data is hampered by its spatial resolution. This means that water bodies and river streams being smaller than the pixel size of 250 m are not included in the geospatial time series. However, we also have to note that consistent geospatial time series featuring multiple decades and high observation intervals are at present only available at the cost of spatial resolution. With respect to this issue, we identified inconsistencies in the Indus river basin, where the main river stream is not always captured. However, mapping of water bodies with optical data at large scale still remains a challenge [96], making the GWP a valuable source to analyze seasonal changes of surface water area. These characteristics also apply on MODIS-based NDVI and GSP.

Furthermore, due to availability of most climate data at monthly temporal resolution and data harmonization purposes, we aggregate daily GWP and GSP time series to monthly scale. When working with MODIS data, future studies could also consider performing investigations at finer temporal granularity such as biweekly intervals instead of monthly. A higher temporal resolution has the potential to enhance the analysis of characteristics in seasonality, as well as the detection of causal links that might disappear due to temporal aggregation to monthly scale.

Moreover, we show that trend analysis requires careful design of the respective tests to derive reliable and comparable results. To this end, we want to highlight the importance in addressing seasonality and serial correlation. However, we add that monotonic trend tests might not be sufficient to evaluate land surface dynamics over multiple decades. Further quantification of changepoints in time series might enhance the analysis and provide more insight into the dynamics. In addition, we demonstrate that our seasonality analysis is capturing grids with one or two growing seasons at the same time. This is important when conducting such analyses at large scale and aiming at using a global setting.

6. Conclusions

In times of accelerating global climate change, the joint analysis of multivariate time series across spheres is crucial to improve our understanding of the interactions within the Earth system. In this context, we used multisource geospatial time series, including vegetation greenness, surface water area, and snow cover area in combination with climatic and hydrological variables over the last two decades to analyze land surface dynamics and driving variables. We developed a novel methodological framework including both the preparation of multisource data to generate a unified feature space as well as the consecutive application of statistical time series analysis techniques. These include the calculation of trends and changes in seasonality, as well as the application of the causal discovery algorithm PCMCI. The findings regarding the employed statistical analyses can be summarized as follows:

• Seasonality and autocorrelation must be dealt with when using the Mann–Kendall test. Thus, we used the seasonal Mann–Kendall test on pre-whitened time series keeping the monthly resolution. At the same time, advantages and disadvantages of pre-whitening algorithms need to be considered. In this regard, experiments suggest not to rely on only a single algorithm;
• Through application of Timesat, we examined the existence of seasonal changes between two decades. For NDVI, we used a global setting considering areas with one and two growing seasons. Although we used monthly time series, we found that the retrieved phenological metrics show consistency with the spatial patterns of positive and negative trends;
• This study is the first to use such a high dimensional feature space for the quantification of drivers of vegetation greenness, surface water area, and snow cover area using the causal discovery algorithm PCMCI. The dependencies between the target and driving variables indicate consistent and homogeneous patterns, confirming its functionality.

Moreover, the analyses for the case study of Indo-Gangetic river basins in South Asia revealed the following:

• MODIS NDVI indicates that greening trends are dominant downstream of the Himalaya-Karakoram. Seasonality of NDVI indicates decreasing seasonal amplitude being accompanied by stable or increasing seasonal peak values. Hence, greening of vegetation in this region is ongoing. We also found that NDVI is mostly impacted by water availability;
• According to the DLR Global Waterpack, negative trends are prominent at the confluence of the Ganges and Brahmaputra rivers and in wetlands of the Meghna basin. Positive trends occur north of the Bay of Bengal and in the Southwest of the Ganges basin. In high altitudes, snow cover and temperature influence surface water area. In the lower river basins, we found discharge and precipitation to be of high relevance;
• The DLR Global Snowpack indicates weak increasing trends over the Upper Indus river basin. Negative trends prevail in the Upper Ganges and Brahmaputra river basins. Accordingly, our results demonstrate that changes in duration of snow cover area match spatial patterns of detected significant trends. Snow cover is largely negatively coupled to temperature, while precipitation shows positive influence over the western Upper Indus river basin.

We want to emphasize that the developed methodological framework is transferable in space and time to any geospatial data and region. In this study, spatial grids were used to unify the multivariate feature space. However, aggregating time series to other geographical entities such as river basins is also possible. Future research will investigate the analysis of time series at finer temporal granularity, e.g., using biweekly instead of monthly observations. This might enhance the analysis of seasonality and the detection of causal links. In addition, further detailed geoscientific analyses are required to attribute land surface dynamics in the context of climate change as well as anthropogenic influences.