Accuracy of Sentinel-1 PSI and SBAS InSAR Displacement Velocities against GNSS and Geodetic Leveling Monitoring Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. SAR Data and Multi-Temporal InSAR Processing
2.2. GNSS Benchmark Monitoring and Data Processing
2.3. Geodetic Leveling
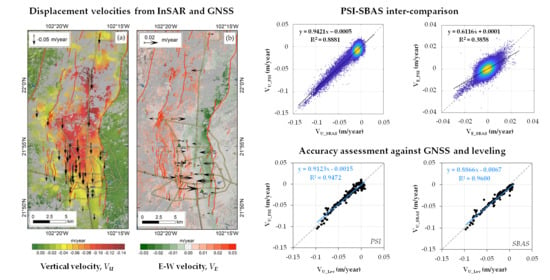
3. Results
3.1. Coverage of InSAR Outputs and Target Visibility
3.2. Observed Displacement Field
3.3. PSI-SBAS Inter-Comparison
3.4. Accuracy of InSAR Displacement Velocity
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bagheri-Gavkosh, M.; Hosseini, S.M.; Ataie-Ashtiani, B.; Sohani, Y.; Ebrahimian, H.; Morovat, F.; Ashrafi, S. Land subsidence: A global challenge. Sci. Total Environ. 2021, 778, 146193. [Google Scholar] [CrossRef] [PubMed]
- Herrera-García, G.; Ezquerro, P.; Tomas, R.; Béjar-Pizarro, M.; López-Vinielles, J.; Rossi, M.; Mateos, R.M.; Carreón-Freyre, D.; Lambert, J.; Teatini, P.; et al. Mapping the global threat of land subsidence. Science 2021, 371, 34–36. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar interferometry and its application to changes in the earth’s surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef] [Green Version]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res. 1989, 94, 9183–9191. [Google Scholar] [CrossRef]
- Casagli, N.; Cigna, F.; Bianchini, S.; Hölbling, D.; Füreder, P.; Righini, G.; Del Conte, S.; Friedl, B.; Schneiderbauer, S.; Iasio, C.; et al. Landslide mapping and monitoring by using radar and optical remote sensing: Examples from the EC-FP7 project SAFER. Remote Sens. Appl. Soc. Environ. 2016, 4, 92–108. [Google Scholar] [CrossRef] [Green Version]
- Raspini, F.; Bianchini, S.; Ciampalini, A.; Del Soldato, M.; Solari, L.; Novali, F.; Del Conte, S.; Rucci, A.; Ferretti, A.; Casagli, N. Continuous, semi-automatic monitoring of ground deformation using Sentinel-1 satellites. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Kalia, A.C.; Frei, M.; Lege, T. A Copernicus downstream-service for the nationwide monitoring of surface displacements in Germany. Remote Sens. Environ. 2017, 202, 234–249. [Google Scholar] [CrossRef]
- Morishita, Y. Nationwide urban ground deformation monitoring in Japan using Sentinel-1 LiCSAR products and LiCSBAS. Prog. Earth Planet. Sci. 2021, 8, 6. [Google Scholar] [CrossRef]
- Lanari, R.; Bonano, M.; Casu, F.; De Luca, C.; Manunta, M.; Manzo, M.; Onorato, G.; Zinno, I. Automatic generation of Sentinel-1 continental scale DInSAR deformation time series through an extended P-SBAS processing pipeline in a cloud computing environment. Remote Sens. 2020, 12, 2961. [Google Scholar] [CrossRef]
- Crosetto, M.; Solari, L.; Mróz, M.; Balasis-Levinsen, J.; Casagli, N.; Frei, M.; Oyen, A.; Moldestad, D.A.; Bateson, L.; Guerrieri, L.; et al. The evolution of wide-area DInSAR: From regional and national services to the European ground motion service. Remote Sens. 2020, 12, 2043. [Google Scholar] [CrossRef]
- Bakon, M.; Czikhardt, R.; Papco, J.; Barlak, J.; Rovnak, M.; Adamisin, P.; Perissin, D. remotIO: A Sentinel-1 multi-temporal InSAR infrastructure monitoring service with automatic updates and data mining capabilities. Remote Sens. 2020, 12, 1892. [Google Scholar] [CrossRef]
- Bohloli, B.; Bjørnarå, T.I.; Park, J.; Rucci, A. Can we use surface uplift data for reservoir performance monitoring? A case study from In Salah, Algeria. Int. J. Greenh. Gas Control 2018, 76, 200–207. [Google Scholar] [CrossRef]
- Adam, N.; Parizzi, A.; Eineder, M.; Crosetto, M. Practical persistent scatterer processing validation in the course of the Terrafirma project. J. Appl. Geophys. 2009, 69, 59–65. [Google Scholar] [CrossRef] [Green Version]
- Cigna, F.; Sowter, A. The relationship between intermittent coherence and precision of ISBAS InSAR ground motion velocities: ERS-1/2 case studies in the UK. Remote Sens. Environ. 2017, 202, 177–198. [Google Scholar] [CrossRef]
- Pepe, A. Multi-temporal small baseline interferometric SAR algorithms: Error budget and theoretical performance. Remote Sens. 2021, 13, 557. [Google Scholar] [CrossRef]
- Ferretti, A.; Savio, G.; Barzaghi, R.; Borghi, A.; Musazzi, S.; Novali, F.; Prati, C.; Rocca, F. Submillimeter accuracy of InSAR time series: Experimental validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1142–1153. [Google Scholar] [CrossRef]
- Quin, G.; Loreaux, P. Submillimeter accuracy of multipass corner reflector monitoring by PS technique. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1775–1783. [Google Scholar] [CrossRef]
- Duan, W.; Zhang, H.; Wang, C.; Tang, Y. Multi-temporal InSAR parallel processing for Sentinel-1 large-scale surface deformation mapping. Remote Sens. 2020, 12, 3749. [Google Scholar] [CrossRef]
- Casu, F.; Manzo, M.; Lanari, R. A quantitative assessment of the SBAS algorithm performance for surface deformation retrieval from DInSAR data. Remote Sens. Environ. 2006, 102, 195–210. [Google Scholar] [CrossRef]
- Bovenga, F.; Nitti, D.O.; Fornaro, G.; Radicioni, F.; Stoppini, A.; Brigante, R. Using C/X-band SAR interferometry and GNSS measurements for the Assisi landslide analysis. Int. J. Remote Sens. 2013, 34, 4083–4104. [Google Scholar] [CrossRef]
- Raucoules, D.; Bourgine, B.; de Michele, M.; Le Cozannet, G.; Closset, L.; Bremmer, C.; Veldkamp, H.; Tragheim, D.; Bateson, L.; Crosetto, M.; et al. Validation and intercomparison of Persistent Scatterers Interferometry: PSIC4 project results. J. Appl. Geophys. 2009, 68, 335–347. [Google Scholar] [CrossRef] [Green Version]
- Manunta, M.; De Luca, C.; Zinno, I.; Casu, F.; Manzo, M.; Bonano, M.; Fusco, A.; Pepe, A.; Onorato, G.; Berardino, P.; et al. The Parallel SBAS approach for Sentinel-1 Interferometric Wide swath deformation time-series generation: Algorithm description and products quality assessment. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6259–6281. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D. Present-day land subsidence rates, surface faulting hazard and risk in Mexico City with 2014–2020 Sentinel-1 IW InSAR. Remote Sens. Environ. 2021, 253, 1–19. [Google Scholar] [CrossRef]
- Aranda Gómez, J.J. Geología preliminar del Graben de Aguascalientes. Rev. Mex. Cienc. Geol. 1989, 8, 22–32. [Google Scholar]
- CONAGUA. Actualización de la Disponibilidad Media Anual de Agua en el Acuífero Valle de Aguascalientes (0101), Estado de Aguascalientes; Diario Oficial de la Federación, 04/01/2018; CONAGUA: Mexico City, Mexico, 2018. [Google Scholar]
- Pacheco-Martínez, J.; Hernandez-Marín, M.; Burbey, T.J.; González-Cervantes, N.; Ortíz-Lozano, J.Á.; Zermeño-De-Leon, M.E.; Solís-Pinto, A. Land subsidence and ground failure associated to groundwater exploitation in the Aguascalientes Valley, México. Eng. Geol. 2013, 164, 172–186. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D. Satellite InSAR survey of structurally-controlled land subsidence due to groundwater exploitation in the Aguascalientes Valley, Mexico. Remote Sens. Environ. 2021, 254, 1–23. [Google Scholar] [CrossRef]
- Esquivel, R.; Castaneda, L.; Taud, H.; Lira, J.; Madero, G.A. Ten years of subsidence monitoring with SAR interferometry and its contribution to risk management in Aguascalientes, Mexico. In Proceedings of the ESA Living Planet Symposium, Edinburgh, UK, 9–13 September 2013; p. 5. [Google Scholar]
- INEGI. Detección de Zonas de Subsidencia en México con Técnicas Satelitales; INEGI: Aguascalientes City, Mexico, 2019. [Google Scholar]
- Yalvaç, S. Validating InSAR-SBAS results by means of different GNSS analysis techniques in medium- and high-grade deformation areas. Environ. Monit. Assess. 2020, 192, 12. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Zhou, X.; Wang, K.; Ke, X.; Zhang, Y.; Zhao, R.; Bao, Y. GOM20: A stable geodetic reference frame for subsidence, faulting, and sea-level rise studies along the coast of the Gulf of Mexico. Remote Sens. 2020, 12, 350. [Google Scholar] [CrossRef] [Green Version]
- SOP. Introducción “SIFAGG”: Sistema de Información de Fallas Geológicas y Grietas; Secretaría de Obras Públicas (SOP) del Gobierno del Estado de Aguascalientes: Aguascalientes, Mexico, 2021. [Google Scholar]
- INEGI. Estudio de los Hundimientos por Subsidencia en Aguascalientes con Métodos Satelitales; Reporte Técnico 2015; INEGI: Aguascalientes, Mexico, 2016; ISBN 978-607-739-808-0. [Google Scholar]
- Esquivel, R.; Hernández, A.; Zermeño, M.E. GPS for Subsidence detection, the case study of Aguascalientes. In Geodetic Deformation Monitoring: From Geophysical to Engineering Roles; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2006; Volume 131, pp. 254–258. [Google Scholar]
- Pepe, A.; Calò, F. A review of Interferometric Synthetic Aperture Radar (InSAR) multi-track approaches for the retrieval of Earth’s surface displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef] [Green Version]
- Farolfi, G.; Bianchini, S.; Casagli, N. Integration of GNSS and satellite InSAR data: Derivation of fine-scale vertical surface motion maps of Po Plain, Northern Apennines, and Southern Alps, Italy. IEEE Trans. Geosci. Remote Sens. 2019, 57, 319–328. [Google Scholar] [CrossRef]
- ESA Sentinel-1 Observation Scenario. Available online: https://sentinel.esa.int/web/sentinel/missions/sentinel-1/observation-scenario (accessed on 26 March 2020).
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.Ö.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- ESA Observation Scenario Archive. Available online: https://sentinels.copernicus.eu/web/sentinel/missions/sentinel-1/observation-scenario/archive (accessed on 13 October 2021).
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Casu, F.; Elefante, S.; Imperatore, P.; Zinno, I.; Manunta, M.; De Luca, C.; Lanari, R. SBAS-DInSAR parallel processing for deformation time-series computation. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2014, 7, 3285–3296. [Google Scholar] [CrossRef]
- Foumelis, M.; Papadopoulou, T.; Bally, P.; Pacini, F.; Provost, F.; Patruno, J. Monitoring Geohazards using on-demand and systematic services on ESA’s Geohazards Exploitation Platform. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 5457–5460. [Google Scholar]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef] [Green Version]
- Cigna, F.; Tapete, D. Sentinel-1 big data processing with P-SBAS InSAR in the Geohazards Exploitation Platform: An experiment on coastal land subsidence and landslides in Italy. Remote Sens. 2021, 13, 885. [Google Scholar] [CrossRef]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arikan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514, 1–13. [Google Scholar] [CrossRef]
- ESA STEP—Science Toolbox Exploitation Platform. Available online: http://step.esa.int/main/ (accessed on 13 October 2021).
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Walters, R.J.; Wright, T.J.; Hooper, A.J.; Parker, D.J. Statistical comparison of InSAR tropospheric correction techniques. Remote Sens. Environ. 2015, 170, 40–47. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Opt. Soc. Am. A 2001, 18, 338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pacheco-Martínez, J.; Cabral-Cano, E.; Wdowinski, S.; Hernández-Marín, M.; Ortiz-Lozano, J.; Zermeño-de-León, M. Application of InSAR and gravimetry for land subsidence hazard Zoning in Aguascalientes, Mexico. Remote Sens. 2015, 7, 17035–17050. [Google Scholar] [CrossRef] [Green Version]
- Cigna, F.; Tapete, D.; Garduño-Monroy, V.H.; Muñiz-Jauregui, J.A.; García-Hernández, O.H.; Jiménez-Haro, A. Wide-area InSAR survey of surface deformation in urban areas and geothermal fields in the eastern Trans-Mexican Volcanic Belt, Mexico. Remote Sens. 2019, 11, 2341. [Google Scholar] [CrossRef] [Green Version]
- Fuhrmann, T.; Garthwaite, M.C. Resolving three-dimensional surface motion with InSAR: Constraints from multi-geometry data fusion. Remote Sens. 2019, 11, 241. [Google Scholar] [CrossRef] [Green Version]
- Cabral-Cano, E.; Pérez-Campos, X.; Márquez-Azúa, B.; Sergeeva, M.A.; Salazar-Tlaczani, L.; DeMets, C.; Adams, D.; Galetzka, J.; Hodgkinson, K.; Feaux, K.; et al. TLALOCNet: A continuous GPS-met backbone in Mexico for seismotectonic and atmospheric research. Seismol. Res. Lett. 2018, 89, 373–381. [Google Scholar] [CrossRef]
- Márquez-Azúa, B.; DeMets, C. Deformation of Mexico from continuous GPS from 1993 to 2008. Geochem. Geophys. Geosystems 2009, 10, 1–16. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef] [Green Version]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. Introduction to GAMIT/GLOBK; Release 10.7; Massachusetts Institute of Technology: Cambridge, MA, USA, 2018. [Google Scholar]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Kouba, J.; Héroux, P. Precise Point Positioning Using IGS Orbit and Clock Products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Beutler, G.; Brockmann, E. Extended orbit modeling techniques at the CODE processing center of the international GPS service for geodynamics (IGS): Theory and initial results. Manuscr. Geod. 1994, 19, 367–386. [Google Scholar]
- Wübbena, G.; Schmitz, M.; Menge, F.; Boder, V.; Seeber, G. Automated Absolute Field Calibration of GPS Antennas in Real-Time. In Proceedings of the 13th International Technical Meeting of the Satellite Division of the Institute of Navigation ION GPS 2000, Salt Lake City, UT, USA, 19–22 September 2000; pp. 1–10. [Google Scholar]
- Rothacher, M. Comparison of Absolute and Relative Antenna Phase Center Variations. GPS Solut. 2001, 4, 55–60. [Google Scholar] [CrossRef]
- Schmid, R.; Steigenberger, P.; Gendt, G.; Ge, M.; Rothacher, M. Generation of a consistent absolute phase-center correction model for GPS receiver and satellite antennas. J. Geod. 2007, 81, 781–798. [Google Scholar] [CrossRef] [Green Version]
- Saastamoinen, J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites. In The Use of Artificial Satellites for Geodesy; American Geophysical Union (AGU): Washington, DC, USA, 1997; pp. 247–251. [Google Scholar]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. Solid Earth 2006, 111, B02406. [Google Scholar] [CrossRef]
- Altamimi, Z.; Métivier, L.; Rebischung, P.; Rouby, H.; Collilieux, X. ITRF2014 plate motion model. Geophys. J. Int. 2017, 209, 1906–1912. [Google Scholar] [CrossRef]
- INEGI. Guía Metodológica de la Red Geodésica Vertical; INEGI: Aguascalientes, Mexico, 2017; 92p. [Google Scholar]
- Castellazzi, P.; Arroyo-Domínguez, N.; Martel, R.; Calderhead, A.I.; Normand, J.C.L.; Gárfias, J.; Rivera, A. Land subsidence in major cities of Central Mexico: Interpreting InSAR-derived land subsidence mapping with hydrogeological data. Int. J. Appl. Earth Obs. Geoinf. 2016, 47, 102–111. [Google Scholar] [CrossRef]
- Hernández-Marín, M.; González-Cervantes, N.; Pacheco-Martínez, J.; Frías-Guzmán, D.H. Discussion on the origin of surface failures in the Valley of Aguascalientes, México. In Proceedings of the International Association of Hydrological Sciences; Copernicus GmbH: Gottingen, Germany, 2015; Volume 372, pp. 235–238. [Google Scholar]
- Liang, C.; Agram, P.; Simons, M.; Fielding, E.J. Ionospheric correction of InSAR time series analysis of C-band sentinel-1 TOPS data. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6755–6773. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi, Z.; Wright, T.J.; Hooper, A.J.; Jordan, C.; Novellino, A.; Bateson, L.; Biggs, J. Benchmarking and inter-comparison of Sentinel-1 InSAR velocities and time series. Remote Sens. Environ. 2021, 256, 112306. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef] [Green Version]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorquí, J.J.; Berardino, P.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Caltagirone, F.; Capuzi, A.; Coletta, A.; De Luca, G.F.; Scorzafava, E.; Leonardi, R.; Rivola, S.; Fagioli, S.; Angino, G.; Labbate, M.; et al. The COSMO-SkyMed dual use Earth observation program: Development, qualification, and results of the commissioning of the overall constellation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2754–2762. [Google Scholar] [CrossRef]

















| Sample | SBAS vs. PSI ΔVU (m/Year) | SBAS vs. PSI ΔVE (m/Year) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size | Min. | Max. | Ave. | Stdv. | RMSE | Size | Min. | Max. | Ave. | Stdv. | RMSE | |
| GNSS benchmarks | 59 | −0.0289 | +0.0148 | −0.0039 | 0.0060 | 0.0071 | 53 | −0.0147 | +0.0111 | −0.0012 | 0.0042 | 0.0043 |
| All targets | 128,772 | −0.0425 | +0.0555 | −0.0003 | 0.0062 | 0.0063 | 75,546 | −0.0471 | +0.0298 | −0.0004 | 0.0039 | 0.0039 |
| InSAR Method | GNSS vs. InSAR ΔVU (m/Year) | Leveling vs. InSAR ΔVU (m/year) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Size | Min. | Max. | Ave. | Stdv. | RMSE | Size | Min. | Max. | Ave. | Stdv. | RMSE | |
| PSI | 62 | −0.0186 | +0.0327 | +0.0039 | 0.0092 | 0.0099 | 172 | −0.0195 | +0.0200 | −0.0034 | 0.0077 | 0.0084 |
| SBAS | 61 | −0.0136 | +0.0355 | +0.0081 | 0.0102 | 0.0130 | 145 | −0.0250 | +0.0251 | +0.0005 | 0.0077 | 0.0077 |
| InSAR Method | GNSS vs. InSAR ΔVE (m/Year) | |||||
|---|---|---|---|---|---|---|
| Size | Min. | Max. | Ave. | Stdv. | RMSE | |
| PSI | 62 | −0.0177 | +0.0194 | −0.0001 | 0.0080 | 0.0079 |
| SBAS | 53 | −0.0149 | +0.0229 | +0.0002 | 0.0076 | 0.0076 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cigna, F.; Esquivel Ramírez, R.; Tapete, D. Accuracy of Sentinel-1 PSI and SBAS InSAR Displacement Velocities against GNSS and Geodetic Leveling Monitoring Data. Remote Sens. 2021, 13, 4800. https://doi.org/10.3390/rs13234800
Cigna F, Esquivel Ramírez R, Tapete D. Accuracy of Sentinel-1 PSI and SBAS InSAR Displacement Velocities against GNSS and Geodetic Leveling Monitoring Data. Remote Sensing. 2021; 13(23):4800. https://doi.org/10.3390/rs13234800
Chicago/Turabian StyleCigna, Francesca, Rubén Esquivel Ramírez, and Deodato Tapete. 2021. "Accuracy of Sentinel-1 PSI and SBAS InSAR Displacement Velocities against GNSS and Geodetic Leveling Monitoring Data" Remote Sensing 13, no. 23: 4800. https://doi.org/10.3390/rs13234800
APA StyleCigna, F., Esquivel Ramírez, R., & Tapete, D. (2021). Accuracy of Sentinel-1 PSI and SBAS InSAR Displacement Velocities against GNSS and Geodetic Leveling Monitoring Data. Remote Sensing, 13(23), 4800. https://doi.org/10.3390/rs13234800