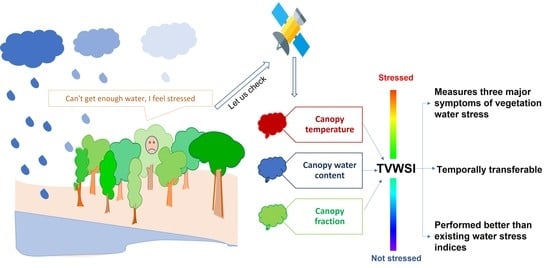
Modeling Vegetation Water Stress over the Forest from Space: Temperature Vegetation Water Stress Index (TVWSI)
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Datasets
2.2.1. MODIS Multispectral and Thermal Infrared Dataset
2.2.2. Meteorological and Model Soil Moisture Data
2.2.3. In Situ Soil Moisture Data
3. Methodology
3.1. Conceptual Model: The Connection between Canopy Temperature, Canopy Water Content, and Canopy Fraction during Soil Moisture Deficits
3.2. Temperature Vegetation Water Stress Index (TVWSI)
3.2.1. SWCI–NDVI Spectral Space and Derivation of d(SWCI, NDVI)
3.2.2. Derivation of TVWSI
3.3. Evaluation of TVWSI
4. Results
4.1. Estimation of d(SWCI, NDVI) from SWCI–NDVI Spectral Space and Analysis of Correlation with AWRA-L Soil Moisture
4.2. Estimation of TVWSI and Analysis of Correlation with AWRA-L Soil Moisture
4.3. Evaluation of TVWSI in Predicting AWRA-L Soil Moisture, and Comparison with Existing Water Stress Metrics
4.4. Evaluation of TVWSI in Predicting Soil Water Fraction (SWF) from Flux Tower Data, and Comparison with Existing Water Stress Metrics
5. Discussion
6. Conclusions
- The intermediate vegetation index d(SWCI, NDVI) is modeled using NDVI and SWCI to simultaneously consider the effects of vegetation growth and vegetation water content. d(SWCI, NDVI) showed an improved correlation with AWRA-L soil moisture than NDVI and SWCI. Moreover, d(SWCI, NDVI) improved retrieving soil moisture dynamics at the lower and higher ranges of soil moisture, which is a significant improvement over the saturation nature of NDVI over high-density vegetation and its inability on open canopy regions;
- Compared to PDI, MPDI, MVWSI, TVDI, and CWSI, the newly devised TVWSI improved prediction ability for the modeled AWRA-L root zone soil moisture from sixty study sampling windows and soil water fraction (SWF) from the four contrasting FLUXNET sites across Victoria and New South Wales;
- As the optical spectral space of SWCI–NDVI and standardized LST is used to model TVWSI, it can be employed to estimate soil moisture dynamics on the temporal data.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.H.; et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. Forest Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Peng, C.; Li, W.; Fang, X.; Zhang, T.; Zhu, Q.; Chen, H.; Zhao, P. Monitoring and estimating drought-induced impacts on forest structure, growth, function, and ecosystem services using remote-sensing data: Recent progress and future challenges. Environ. Rev. 2013, 21, 103–115. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Cao, B.; Liu, S.; Yu, G.; Jia, K.; Zhang, X.; Zhang, Y.; Chen, J.; Fisher, J.B. Satellite detection of water stress effects on terrestrial latent heat flux with MODIS shortwave infrared reflectance data. J. Geophys. Res. Atmos. 2018, 123, 11–410. [Google Scholar] [CrossRef] [Green Version]
- Evans, B.; Stone, C.; Barber, P. Linking a decade of forest decline in the south-west of western Australia to bioclimatic change. Aust. For. 2013, 76, 164–172. [Google Scholar] [CrossRef]
- Fensham, R.J.; Fairfax, R.J.; Butler, D.W.; Bowman, D.M.J.S. Effects of fire and drought in a tropical eucalypt savanna colonized by rain forest. J. Biogeogr. 2003, 30, 1405–1414. [Google Scholar] [CrossRef]
- Fensham, R.J.; Fairfax, R.J. Drought-related tree death of savanna eucalypts: Species susceptibility, soil conditions and root architecture. J. Veg. Sci. 2007, 18, 71–80. [Google Scholar] [CrossRef]
- Fensham, R.J.; Fairfax, R.J.; Ward, D.P. Drought-induced tree death in savanna. Glob. Chang. Biol. 2009, 15, 380–387. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, P.J.; O’Grady, A.P.; Hayes, K.R.; Pinkard, E.A. Exposure of trees to drought-induced die-off is defined by a common climatic threshold across different vegetation types. Ecol. Evol. 2014, 4, 1088–1101. [Google Scholar] [CrossRef]
- Mitchell, P.J.; Benyon, R.G.; Lane, P.N.J. Responses of evapotranspiration at different topographic positions and catchment water balance following a pronounced drought in a mixed species eucalypt forest, Australia. J. Hydrol. 2012, 440–441, 62–74. [Google Scholar] [CrossRef]
- Crausbay, S.D.; Ramirez, A.R.; Carter, S.L.; Cross, M.S.; Hall, K.R.; Bathke, D.J.; Betancourt, J.L.; Colt, S.; Cravens, A.E.; Dalton, M.S.; et al. Defining ecological drought for the twenty-first century. Bull. Am. Meteorol. Soc. 2017, 98, 2543–2550. [Google Scholar] [CrossRef]
- Allen, C.D.; Breshears, D.D.; McDowell, N.G. On underestimation of global vulnerability to tree mortality and forest die-off from hotter drought in the Anthropocene. Ecosphere 2015, 6, 129. [Google Scholar] [CrossRef]
- Hinckley, T.; Lassoie, J.; Running, S. Temporal and spatial variations in the water status of forest trees. For. Sci. 1978, 24, a0001-z0001. [Google Scholar]
- Jacquart, E.M.; Armentano, T.V.; Spingarn, A.L. Spatial and temporal tree responses to water stress in an old-growth deciduous forest. Am. Midl. Nat. 1992, 127, 158–171. [Google Scholar] [CrossRef]
- Amani, M.; Parsian, S.; MirMazloumi, S.M.; Aieneh, O. Two new soil moisture indices based on the nir-red triangle space of landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2016, 50, 176–186. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Masjedi, A.; Dehnavi, S. Temperature-vegetation-soil moisture dryness index (TVMDI). Remote Sens. Environ. 2017, 197, 1–14. [Google Scholar] [CrossRef]
- Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
- Rahimzadeh-Bajgiran, P.; Omasa, K.; Shimizu, Y. Comparative evaluation of the vegetation dryness index (VDI), the temperature vegetation dryness index (TVDI) and the improved TVDI (iTVDI) for water stress detection in semi-arid regions of Iran. ISPRS J. Photogramm. Remote Sens. 2012, 68, 1–12. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Sun, L.; Sun, R.; Li, X.; Liang, S.; Zhang, R. Monitoring surface soil moisture status based on remotely sensed surface temperature and vegetation index information. Agric. Forest Meteorol. 2012, 166–167, 175–187. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United states based on thermal remote sensing: 1. Model formulation. J. Geophys. Res. Atmos. 2007, 112, 1–17. [Google Scholar] [CrossRef]
- Carlson, T.N.; Gillies, R.R.; Perry, E.M. A method to make use of thermal infrared temperature and NDVI measurements to infer surface soil water content and fractional vegetation cover. Remote Sens. Rev. 1994, 9, 161–173. [Google Scholar] [CrossRef]
- Goward, S.N.; Cruickshanks, G.D.; Hope, A.S. Observed relation between thermal emission and reflected spectral radiance of a complex vegetated landscape. Remote Sens. Environ. 1985, 18, 137–146. [Google Scholar] [CrossRef]
- Lambin, E.F.; Ehrlich, D. The surface temperature-vegetation index space for land cover and land-cover change analysis. Int. J. Remote Sens. 1996, 17, 463–487. [Google Scholar] [CrossRef]
- Nemani, R.; Pierce, L.; Running, S.; Goward, S. Developing satellite-derived estimates of surface moisture status. J. Appl. Meteorol. 1993, 32, 548–557. [Google Scholar] [CrossRef] [Green Version]
- Nemani, R.R.; Running, S.W. Estimation of Regional Surface Resistance to Evapotranspiration from NDVI and Thermal-IR AVHRR Data. J. Appl. Meteorol. 1989, 28, 276–284. [Google Scholar] [CrossRef]
- Smith, R.C.G.; Choudhury, B.J. Analysis of normalized difference and surface temperature observations over southeastern Australia. Int. J. Remote Sens. 1991, 12, 2021–2044. [Google Scholar] [CrossRef]
- Goward, S.N.; Hope, A.S. Evapotranspiration from combined reflected solar and emitted terrestrial radiation: Preliminary fife results from AVHRR data. Adv. Space Res. 1989, 9, 239–249. [Google Scholar] [CrossRef]
- Price, J.C. Using spatial context in satellite data to infer regional scale evapotranspiration. IEEE Trans. Geosci. Remote Sens. 1990, 28, 940–948. [Google Scholar] [CrossRef] [Green Version]
- Wan, Z.; Wang, P.; Li, X. Using MODIS land surface temperature and normalized difference vegetation index products for monitoring drought in the southern Great Plains, USA. Int. J. Remote Sens. 2004, 25, 61–72. [Google Scholar] [CrossRef]
- Goward, S.N.; Xue, Y.; Czajkowski, K.P. Evaluating land surface moisture conditions from the remotely sensed temperature/vegetation index measurements: An exploration with the simplified simple biosphere model. Remote Sens. Environ. 2002, 79, 225–242. [Google Scholar] [CrossRef]
- Han, Y.; Wang, Y.; Zhao, Y. Estimating soil moisture conditions of the Greater Changbai Mountains by land surface temperature and NDVI. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2509–2515. [Google Scholar]
- Mallick, K.; Bhattacharya, B.K.; Patel, N.K. Estimating volumetric surface moisture content for cropped soils using a soil wetness index based on surface temperature and NDVI. Agric. For. Meteorol. 2009, 149, 1327–1342. [Google Scholar] [CrossRef]
- Wang, W.; Huang, D.; Wang, X.G.; Liu, Y.R.; Zhou, F. Estimation of soil moisture using trapezoidal relationship between remotely sensed land surface temperature and vegetation index. Hydrol. Earth Syst. Sci. 2011, 15, 1699–1712. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Wu, L.; Yue, H. Biparabolic NDVI-Ts space and soil moisture remote sensing in an arid and semi arid area. Can. J. Remote Sens. 2015, 41, 159–169. [Google Scholar] [CrossRef]
- Carlson, T.N. Remote estimation of soil moisture availability and fractional vegetation cover for agricultural fields. Agric. For. Meteorol. 1990, 52, 45–69. [Google Scholar] [CrossRef]
- Cai, G.; Du, M.; Liu, Y. Regional drought monitoring and analyzing using MODIS data—A case study in Yunnan Province. In Proceedings of the 4th Conference on Computer and Computing Technologies in Agriculture (CCTA), Nanchang, China, 22–25 October 2010; pp. 243–251. [Google Scholar]
- Wu, M.-X.; Lu, H.-Q. A modified vegetation water supply index (MVWSI) and its application in drought monitoring over Sichuan and Chongqing, China. J. Integr. Agric. 2016, 15, 2132–2141. [Google Scholar] [CrossRef]
- Wang, P.X.; Li, X.W.; Gong, J.Y.; Song, C. Vegetation temperature condition index and its application for drought monitoring. In Proceedings of the IEEE 2001 International Geoscience and Remote Sensing Symposium (IGARSS 2001) (Cat. No. 01CH37217), Sydney, NSW, Australia, 9–13 July 2001; pp. 141–143. [Google Scholar]
- Kogan, F.N. Remote sensing of weather impacts on vegetation in non-homogeneous areas. Int. J. Remote Sens. 1990, 11, 1405–1419. [Google Scholar] [CrossRef]
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- McVicar, T.R.; Bierwirth, P.N. Rapidly assessing the 1997 drought in Papua New Guinea using composite AVHRR imagery. Int. J. Remote Sens. 2001, 22, 2109–2128. [Google Scholar] [CrossRef]
- Sun, H. Two-stage trapezoid: A new interpretation of the land surface temperature and fractional vegetation coverage space. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 336–346. [Google Scholar] [CrossRef]
- Tao, L.; Ryu, D.; Western, A.; Boyd, D. A new drought index for soil moisture monitoring based on MPDI-NDVI trapezoid space using MODIS data. Remote Sens. 2021, 13, 122. [Google Scholar] [CrossRef]
- Ghulam, A.; Li, Z.; Qin, Q.; Tong, Q. Exploration of the spectral space based on vegetation index and albedo for surface drought estimation. J. Appl. Remote Sens. 2007, 1, 013529. [Google Scholar]
- Ghulam, A.; Qin, Q.; Zhan, Z. Designing of the perpendicular drought index. Environ. Geol. 2007, 6, 1045–1052. [Google Scholar] [CrossRef]
- Ghulam, A.; Qin, Q.; Teyip, T.; Li, Z.-L. Modified perpendicular drought index (MPDI): A real-time drought monitoring method. ISPRS J. Photogramm. Remote Sens. 2007, 62, 150–164. [Google Scholar] [CrossRef]
- Ghulam, A.; Li, Z.-L.; Qin, Q.; Tong, Q.; Wang, J.; Kasimu, A.; Zhu, L. A method for canopy water content estimation for highly vegetated surfaces-shortwave infrared perpendicular water stress index. Sci. China Ser. D Earth Sci. 2007, 50, 1359–1368. [Google Scholar] [CrossRef]
- Serrano, L.; Ustin, S.L.; Roberts, D.A.; Gamon, J.A.; Peñuelas, J. Deriving water content of chaparral vegetation from AVIRIS data. Remote Sens. Environ. 2000, 74, 570–581. [Google Scholar] [CrossRef]
- Zhang, N.; Hong, Y.; Qin, Q.; Liu, L. VSDI: A visible and shortwave infrared drought index for monitoring soil and vegetation moisture based on optical remote sensing. Int. J. Remote Sens. 2013, 34, 4585–4609. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J.; Hao, X.; Zhu, Q. Sensitivity studies of the moisture effects on MODIS SWIR reflectance and vegetation water indices. Int. J. Remote Sens. 2008, 29, 7065–7075. [Google Scholar] [CrossRef]
- Cheng, Y.-B.; Ustin, S.L.; Riaño, D.; Vanderbilt, V.C. Water content estimation from hyperspectral images and MODIS indexes in Southeastern Arizona. Remote Sens. Environ. 2008, 112, 363–374. [Google Scholar] [CrossRef]
- Jackson, T.J.; Chen, D.; Cosh, M.H.; Li, F.; Anderson, M.C.; Walthall, C.L.; Doriaswamy, P.; Hunt, E.R. Vegetation water content mapping using landsat data derived normalized difference water index for corn and soybeans. Remote Sens. Environ. 2004, 92, 475–482. [Google Scholar] [CrossRef]
- BOM. Climate Statistics for Australian Locations—Quambone; Bureau of Meteorology: Melbourne, VIC, Australia, 2010.
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the köppen-geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
- DSE. Native Vegetation–Glossary; Department of Sustainability & Environment: Melbourne, VIC, Australia, 2007.
- Specht, R.L. Foliage projective cover and standing biomass. In Vegetation Classification in Australia; Gillson, A.N., Anderson, D.J., Eds.; Commonwealth Scientific and Industrial Research Organization: Canberra, ACT, Australia, 1981; pp. 10–21. [Google Scholar]
- Schaaf, C.; Wang, Z. Mcd43a1 modis/terra+aqua brdf/albedo Model Parameters Daily l3 Global-500 m v006. [Data Set]. NASA EOSDIS Land Processes DAAC. 2015. Available online: https://lpdaac.usgs.gov/products/mcd43a4v006/ (accessed on 29 August 2021).
- Wan, Z.; Hook, S.; Hulley, G. Myd11a1 MODIS/aqua Land Surface Temperature/Emissivity Daily L3 Global 1 km SIN Grid v006. Nasa Eosdis Land Processes Daac; 2015. 2021. Available online: https://lpdaac.usgs.gov/products/myd11a1v006/ (accessed on 29 August 2021).
- Van Dijk, A.; Warren, G. The Australian Water Resources Assessment System, Version 0.5; CSIRO: Canberra, ACT, Australia, 2010.
- Frost, A.J.; Ramchurn, A.; Smith, A. The Australian Landscape Water Balance Model (awra-l v6). Technical Description of the Australian Water Resources Assessment Landscape Model Version 6; Bureau of Meteorology: Melbourne, VIC, Australia, 2018.
- Renzullo, L.J.; van Dijk, A.I.J.M.; Perraud, J.M.; Collins, D.; Henderson, B.; Jin, H.; Smith, A.B.; McJannet, D.L. Continental satellite soil moisture data assimilation improves root-zone moisture analysis for water resources assessment. J. Hydrol. 2014, 519, 2747–2762. [Google Scholar] [CrossRef]
- van Dijk, A.I.J.M.; Beck, H.E.; Crosbie, R.S.; de Jeu, R.A.M.; Liu, Y.Y.; Podger, G.M.; Timbal, B.; Viney, N.R. The millennium drought in Southeast Australia (2001–2009): Natural and human causes and implications for water resources, ecosystems, economy, and society. Water Resour. Res. 2013, 49, 1040–1057. [Google Scholar] [CrossRef]
- Frost, A.J.a.W.; David, P. The Australian water resource assessment landscape model—Awra-l: Improved performance and regional calibration. In Proceedings of the 38th Hydrology and Water Resources Symposium (HWRS 2018): Water and Communities. Engineers Australia, Melbourne, VIC, Australia, 3–6 December 2018; pp. 933–949. [Google Scholar]
- Frost, A.J.; Donelly, C. Evaluation of the Australian Landscape Water Balance Model: Awra-l v6; Bureau of Meteorology: Melbourne, VIC, Australia, 2018.
- Zhang, Y.V.; Viney, N.; Frost, A.; Oke, A.; Brooks, M.; Chen, Y.; Campbell, N. Collation of Australian Modeller’s Streamflow Dataset for 780 Unregulated Australian Catchments; Australian Bureau of Meteorology: Melbourne, VIC, Australia, 2013.
- Rüdiger, C.; Hancock, G.; Hemakumara, H.M.; Jacobs, B.; Kalma, J.D.; Martinez, C.; Thyer, M.; Walker, J.P.; Wells, T.; Willgoose, G.R. Goulburn river experimental catchment data set. Water Resour. Res. 2007, 43, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Beringer, J.; Hutley, L.B.; McHugh, I.; Arndt, S.K.; Campbell, D.; Cleugh, H.A.; Cleverly, J.; Víctor Resco de, D.; Eamus, D.; Evans, B.; et al. An introduction to the Australian and New Zealand flux tower network—Ozflux. Biogeosciences 2016, 13, 5895–5916. [Google Scholar] [CrossRef] [Green Version]
- Baldocchi, D. Breathing of the terrestrial biosphere: Lessons learned from a global network of carbon dioxide flux measurement systems. Aust. J. Bot. 2008, 56, 1–26. [Google Scholar] [CrossRef]
- Arndt, S. Wombat State Forest OzFlux-Tower Site OzFlux: Australian and New Zealand Flux Research And Monitoring. 2013. Available online: https://researchdata.edu.au/wombat-state-forest-tower-site/449251 (accessed on 29 August 2021).
- Beringer, J. Wallaby Creek OzFlux Tower Site. OzFlux: Australian and New Zealand Flux Research and Monitoring. 2013. Available online: https://researchdata.edu.au/wallaby-creek-ozflux-tower-site/449252 (accessed on 29 August 2021).
- Beringer, J. Whroo OzFlux Tower Site. OzFlux: Australian and New Zealand Flux Research and Monitoring. 2013. Available online: https://researchdata.edu.au/whroo-ozflux-tower-site/449276 (accessed on 29 August 2021).
- Woodgate, W. Tumbarumba OzFlux Tower Site. OzFlux: Australian and New Zealand Flux Research and Monitoring. 2013. Available online: https://researchdata.edu.au/tumbarumba-ozflux-tower-site/449253 (accessed on 29 August 2021).
- Pahlevan, N.; Roger, J.C.; Ahmad, Z. Revisiting short-wave-infrared (SWIR) bands for atmospheric correction in coastal waters. Opt. Express 2017, 25, 6015–6035. [Google Scholar] [CrossRef]
- Trent, T.; Boesch, H.; Somkuti, P.; Scott, N.A. Observing water vapour in the planetary boundary layer from the short-wave infrared. Remote Sens. 2018, 10, 1469. [Google Scholar] [CrossRef] [Green Version]
- Du, X.; Wang, S.; Zhou, Y.; Wei, H. Construction and validation of a new model for unified surface water capacity based on MODIS data. Geomat. Inf. Sci. Wuhan Univ. 2007, 32, 205–207. [Google Scholar]
- Zhang, H.; Chen, H.; Sun, R.; Yu, W.; Zou, C.; Shen, S. The application of unified surface water capacity method in drought remote sensing monitoring. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XI; International Society for Optics and Photonics: Bellingham, WA, USA, 2009; p. 74721M. [Google Scholar]
- Huete, A.; Justice, C.; Liu, H. Development of vegetation and soil indices for MODIS-EOS. Remote Sens. Environ. 1994, 49, 224–234. [Google Scholar] [CrossRef]
- Huete, A.; Justice, C.; van Leeuwen, W. Modis Vegetation Index (mod13) Algorithm Theoretical Basis Document; Version 3; University of Arizona: Tucson, AZ, USA, 1999. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Xie, H.; Guan, H.; Zhou, X. Different responses of MODIS-derived NDVI to root-zone soil moisture in semi-arid and humid regions. J. Hydrol. 2007, 340, 12–24. [Google Scholar] [CrossRef]
- Crow, W.T.; Kustas, W.P.; Prueger, J.H. Monitoring root-zone soil moisture through the assimilation of a thermal remote sensing-based soil moisture proxy into a water balance model. Remote Sens. Environ. 2008, 112, 1268–1281. [Google Scholar] [CrossRef]
- Liu, S.; Roberts, D.A.; Chadwick, O.A.; Still, C.J. Spectral responses to plant available soil moisture in a Californian grassland. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 31–44. [Google Scholar] [CrossRef]
- Schnur, M.T.; Xie, H.; Wang, X. Estimating root zone soil moisture at distant sites using MODIS NDVI and EVI in a semi-arid region of southwestern USA. Ecol. Inform. 2010, 5, 400–409. [Google Scholar] [CrossRef]
- Peng, C.; Deng, M.; Di, L. Relationships between remote-sensing-based agricultural drought indicators and root zone soil moisture: A comparative study of Iowa. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4572–4580. [Google Scholar] [CrossRef]
- Santos, W.J.R.; Silva, B.M.; Oliveira, G.C.; Volpato, M.M.L.; Lima, J.M.; Curi, N.; Marques, J.J. Soil moisture in the root zone and its relation to plant vigor assessed by remote sensing at management scale. Geoderma 2014, 221–222, 91–95. [Google Scholar] [CrossRef]
- Sadeghi, M.; Babaeian, E.; Tuller, M.; Jones, S.B. The optical trapezoid model: A novel approach to remote sensing of soil moisture applied to sentinel-2 and landsat-8 observations. Remote Sens. Environ. 2017, 198, 52–68. [Google Scholar] [CrossRef] [Green Version]
- Sturges, H.A. The choice of a class interval. J. Am. Stat. Assoc. 1926, 21, 65–66. [Google Scholar] [CrossRef]
- Goetz, S.J. Multi-sensor analysis of NDVI, surface temperature and biophysical variables at a mixed grassland site. Int. J. Remote Sens. 1997, 18, 71–94. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D.; Pinter, P.J.; Reginato, R.J.; Hatfield, J.L. Normalizing the stress-degree-day parameter for environmental variability. Agric. Meteorol. 1981, 24, 45–55. [Google Scholar] [CrossRef]
- Ahmed, M.; Else, B.; Eklundh, L.; Ardö, J.; Seaquist, J. Dynamic response of NDVI to soil moisture variations during different hydrological regimes in the Sahel region. Int. J. Remote Sens. 2017, 38, 5408–5429. [Google Scholar] [CrossRef]
- Chen, T.; de Jeu, R.A.M.; Liu, Y.Y.; van der Werf, G.R.; Dolman, A.J. Using satellite based soil moisture to quantify the water driven variability in NDVI: A case study over mainland Australia. Remote Sens. Environ. 2014, 140, 330–338. [Google Scholar] [CrossRef]
- De Keersmaecker, W.; Lhermitte, S.; Hill, M.J.; Tits, L.; Coppin, P.; Somers, B. Assessment of regional vegetation response to climate anomalies: A case study for Australia using GIMMS NDVI time series between 1982 and 2006. Remote Sens. 2017, 9, 34. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Santin-Janin, H.; Garel, M.; Chapuis, J.L.; Pontier, D. Assessing the performance of NDVI as a proxy for plant biomass using non-linear models: A case study on the Kerguelen archipelago. Polar Biol. 2009, 32, 861–871. [Google Scholar] [CrossRef]
- Van Hoek, M.; Jia, L.; Zhou, J.; Zheng, C.; Menenti, M. Early drought detection by spectral analysis of satellite time series of precipitation and normalized difference vegetation index (NDVI). Remote Sens. 2016, 8, 422. [Google Scholar] [CrossRef] [Green Version]
- Jackson, R.; Reginato, R.; Idso, S. Wheat canopy temperature: A practical tool for evaluating water requirements. Water Resour. Res. 1977, 13, 651–656. [Google Scholar] [CrossRef]
- Jackson, R.D.; Idso, S.B.; Reginato, R.J.; Pinter, P.J., Jr. Canopy temperature as a crop water stress indicator. Water Resour. Res. 1981, 17, 1133–1138. [Google Scholar] [CrossRef]
- Schmugge, T. Remote sensing of surface soil moisture. J. Appl. Meteorol. 1978, 17, 1549–1557. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Zhou, G. Estimation of soil moisture from optical and thermal remote sensing: A review. Sensors 2016, 16, 1308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Rich, P.M.; Price, K.P. Temporal responses of NDVI to precipitation and temperature in the central great plains, USA. Int. J. Remote Sens. 2003, 24, 2345–2364. [Google Scholar] [CrossRef]
- Hong, Z.; Zhang, W.; Yu, C.; Zhang, D.; Li, L.; Meng, L. Swcti: Surface water content temperature index for assessment of surface soil moisture status. Sensors 2018, 18, 2875. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Famiglietti, J.S.; Ryu, D.; Berg, A.A.; Rodell, M.; Jackson, T.J. Field observations of soil moisture variability across scales. Water Resour. Res. 2008, 44, 1–16. [Google Scholar] [CrossRef] [Green Version]












| Indices | References |
|---|---|
| [45] | |
| [46] | |
| [37] | |
| [18] | |
| [89] |
| VI’s | Actual vs. Predicted AWRA-L Soil Moisture (R2) | RMSE (mm) | ||||
|---|---|---|---|---|---|---|
| 1st-Order Polynomial Model | 2nd-Order Polynomial Model | 3rd-Order Polynomial Model | 1st-Order Polynomial Model | 2nd-Order Polynomial Model | 3rd-Order Polynomial Model | |
| Proposed vegetation water stress index | ||||||
| TVWSI | 0.71 | 0.71 | 0.72 | 21.82 | 21.8 | 21.38 |
| Existing vegetation water stress indices | ||||||
| MVWSI | 0.49 | 0.54 | 0.55 | 28.98 | 27.51 | 27.44 |
| CWSI | 0.42 | 0.42 | 0.43 | 31.14 | 30.89 | 30.71 |
| PDI | 0.29 | 0.29 | 0.31 | 34.39 | 34.27 | 33.70 |
| MPDI | 0.20 | 0.20 | 0.23 | 36.45 | 36.36 | 35.80 |
| TVDI | 0.19 | 0.19 | 0.20 | 36.68 | 36.53 | 36.49 |
| Vegetation Water Stress Index | Whroo | Wallaby | Wombat | Tumbarumba | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| TVWSI | 0.25 | 0.029 | 0.43 | 0.024 | 0.51 | 0.032 | 0.44 | 0.040 |
| MVWSI | 0.21 | 0.035 | 0.20 | 0.029 | 0.33 | 0.038 | 0.23 | 0.047 |
| TVDI | 0.20 | 0.035 | 0.29 | 0.027 | 0.24 | 0.040 | 0.17 | 0.048 |
| PDI | 0.08 | 0.038 | 0.10 | 0.030 | 0.32 | 0.038 | 0.00 | 0.053 |
| MPDI | 0.07 | 0.038 | 0.10 | 0.030 | 0.27 | 0.039 | 0.00 | 0.053 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joshi, R.C.; Ryu, D.; Sheridan, G.J.; Lane, P.N.J. Modeling Vegetation Water Stress over the Forest from Space: Temperature Vegetation Water Stress Index (TVWSI). Remote Sens. 2021, 13, 4635. https://doi.org/10.3390/rs13224635
Joshi RC, Ryu D, Sheridan GJ, Lane PNJ. Modeling Vegetation Water Stress over the Forest from Space: Temperature Vegetation Water Stress Index (TVWSI). Remote Sensing. 2021; 13(22):4635. https://doi.org/10.3390/rs13224635
Chicago/Turabian StyleJoshi, Rakesh Chandra, Dongryeol Ryu, Gary J. Sheridan, and Patrick N. J. Lane. 2021. "Modeling Vegetation Water Stress over the Forest from Space: Temperature Vegetation Water Stress Index (TVWSI)" Remote Sensing 13, no. 22: 4635. https://doi.org/10.3390/rs13224635
APA StyleJoshi, R. C., Ryu, D., Sheridan, G. J., & Lane, P. N. J. (2021). Modeling Vegetation Water Stress over the Forest from Space: Temperature Vegetation Water Stress Index (TVWSI). Remote Sensing, 13(22), 4635. https://doi.org/10.3390/rs13224635