The Influence of Shadow Effects on the Spectral Characteristics of Glacial Meltwater
Abstract
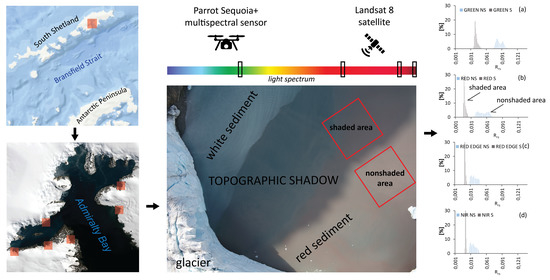
:1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Unmanned Aerial Vehicle (UAV) and Satellite Data Acquisition
2.3. Post-Processing
2.3.1. Digital Surface Model (DSM) and Ortho-mosaic
2.3.2. Hillshade Model and Aspects
- The first distribution involved the percentage of the shadow area on the glacier cove on the day and at the time (10:15 a.m. local time, UTC-3) of the Landsat satellite flight over King George Island (data obtained from the Landsat acquisition tool).
- The second distribution presented the daily shadows on the 15th of each month at hourly intervals from 6 a.m. to 6 p.m.
2.3.3. Remote Sensing (RRS) Reflectance Map
2.3.4. Shadow Detection
2.3.5. Sampling Areas
2.4. Shortwave Radiation Data Acquisition
3. Results
3.1. Spatial and Temporal Distributions of Shadows
3.2. Spectral Characteristics of the Sampling Area on UAV Multispectral Imagery
3.2.1. Shortwave Radiation Data
3.2.2. Spectral Characteristic for Investigated Cases
3.2.3. Spectral Characteristics of Aggregated Pixels of UAV Images and Pixels of Satellite Imagery
4. Discussion
5. Conclusions
- Shadows significantly affect the spectral properties of meltwater, reducing the amount of reflected radiation. Ocean color radiometry, which is based on very low radiation values, is relevant because it can cause significant differences.
- UAV images enable the determination of spatial changes in the spectral characteristics of shaded water:
- (a)
- A uniform surface of shaded water (low turbidity and no ice phenomena) tends to change its spectral properties during the approach to an obstacle casting a shadow.
- (b)
- With highly turbid, shallow water and ice phenomena, spatial tendency does not occur. In this case, the spectral signature depends on the sediment type and the saturation of the SSC surface water layer.
- (c)
- Within highly suspended water, the difference in reflection in the shaded and nonshaded areas will be smaller.
- (d)
- Ice and a shallow bottom in the immediate vicinity of the glacier front in the shaded area may disturb the analysis.
- (e)
- The difference between the amount of radiation reflected in the shaded and nonshaded areas depends on the amount of shortwave downward radiation (time of the day).
- Pixel aggregation of uniform areas causes the loss of detailed information, while pixel aggregation of nonuniform, shallow areas with ice phenomena causes changes and the loss of original information.
- The reflection in the satellite imagery is much smaller in both the nonshaded and shaded areas than in the UAV images. In NIRs, shifts between shadow and nonshadow areas are often close to 0 or even negative.
- The characteristics of the spectral bands in the shaded area are as follows:
- (a)
- The green spectral band has the highest contrast in the amount of reflected radiation between NS and S, but due to its high sensitivity, the analysis can be overestimated.
- (b)
- In the RE and NIR, the values in shaded areas are uniform and without contrast, which makes it impossible to obtain primary information about the spectral characteristics of water.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Zalewski 1 | ||||||||||||||||||||||
| 1.1/1.2 | 2.1/2.2 | 3.1/3.2 | 4.1/4.2 | |||||||||||||||||||
| GR | RD | RG | NIR | GR | RD | RG | NIR | GR | RD | RG | NIR | GR | RD | RG | NIR | |||||||
| GR | + | + | + | + | ||||||||||||||||||
| RD | + | + | + | + | ||||||||||||||||||
| RG | + | + | + | + | ||||||||||||||||||
| NIR | + | + | + | + | ||||||||||||||||||
| Zalewski 2 | ||||||||||||||||||||||
| GR | + | + | + | + | ||||||||||||||||||
| RD | + | + | + | + | ||||||||||||||||||
| RG | + | - | + | + | ||||||||||||||||||
| NIR | + | + | + | + | ||||||||||||||||||
| Zalewski 3 | ||||||||||||||||||||||
| GR | + | + | + | + | ||||||||||||||||||
| RD | + | + | + | + | ||||||||||||||||||
| RG | + | + | + | + | ||||||||||||||||||
| NIR | + | + | + | + | ||||||||||||||||||
| Krak 1 | ||||||||||||||||||||||
| GR | + | |||||||||||||||||||||
| RD | + | |||||||||||||||||||||
| RG | + | |||||||||||||||||||||
| NIR | + | |||||||||||||||||||||
| Zalewski 1 | ||||||||||||||||
| 1.1/1.2 | 2.1/2.2 | 3.1/3.2 | 4.1/4.2 | |||||||||||||
| Differences in: * | GR | RD | RG | NIR | GR | RD | RG | NIR | GR | RD | RG | NIR | GR | RD | RG | NIR |
| range | 0.032 | 0.048 | 0.028 | 0.0237 | 0.004 | 0.012 | 0.005 | 0.008 | 0.0105 | 0.030 | 0.017 | 0.0113 | 0.100 | 0.036 | 0.042 | 0.044 |
| median | 0.041 | 0.035 | 0.018 | 0.015 | 0.036 | 0.014 | 0.005 | 0.004 | 0.047 | 0.014 | 0.006 | 0.005 | 0.022 | 0.007 | 0.005 | 0.005 |
| max. values | 0.063 | 0.066 | 0.036 | 0.031 | 0.032 | 0.020 | 0.008 | 0.010 | 0.044 | 0.039 | 0.020 | 0.014 | 0.108 | 0.036 | 0.042 | 0.044 |
| Zalewski 2 | ||||||||||||||||
| range * | −0.006 | 0.008 | 0.025 | 0.008 | 0.066 | −0.025 | 0.025 | 0.012 | 0.005 | −0.005 | 0.023 | 0.006 | 0.014 | 0.004 | 0.106 | 0.015 |
| median * | 0.070 | 0.004 | 0.029 | 0.004 | 0.079 | 0.003 | 0.034 | 0.003 | 0.070 | 0.004 | 0.029 | 0.004 | 0.060 | 0.008 | 0.014 | 0.001 |
| max. values * | 0.100 | 0.087 | 0.027 | 0.023 | 0.110 | 0.041 | −0.021 | 0.015 | 0.114 | 0.086 | 0.026 | 0.031 | −0.209 | −0.165 | −0.220 | −0.215 |
| Zalewski 3 | ||||||||||||||||
| range * | 0.135 | 0.132 | 0.276 | 0.243 | 0.165 | 0.112 | 0.121 | 0.082 | 0.041 | 0.018 | 0.007 | 0.007 | 0.161 | 0.101 | 0.039 | 0.028 |
| median * | 0.141 | 0.162 | 0.099 | 0.083 | 0.128 | 0.076 | 0.042 | 0.033 | 0.105 | 0.053 | 0.020 | 0.014 | 0.178 | 0.116 | 0.042 | 0.029 |
| max. values * | 0.247 | 0.256 | 0.350 | 0.308 | 0.211 | 0.150 | 0.142 | 0.099 | 0.134 | 0.063 | 0.022 | 0.016 | 0.197 | 0.136 | 0.054 | 0.037 |
| Krak 1 | ||||||||||||||||
| range * | −0.122 | −0.066 | −0.040 | −0.016 | ||||||||||||
| median * | 0.066 | 0.096 | 0.125 | 0.122 | ||||||||||||
| max. values * | −0.042 | 0.048 | 0.094 | 0.111 | ||||||||||||




References
- Frederikse, T.; Landerer, F.; Caron, L.; Adhikari, S.; Parkes, D.; Humphrey, V.; Dangendorf, S.; Hogarth, P.; Zanna, L.; Cheng, L.; et al. The causes of sea-level rise since 1900. Nature 2020, 584, 393–397. [Google Scholar] [CrossRef] [PubMed]
- Aracena, C.; González, H.E.; Garcés-Vargas, J.; Lange, C.B.; Pantoja, S.; Muñoz, F.; Teca, E.; Tejos, E. Influence of summer conditions on surface water properties and phytoplankton productivity in embayments of the South Shetland Islands. Polar Biol. 2018, 41, 2135–2155. [Google Scholar] [CrossRef]
- Meredith, M.P.; Falk, U.; Bers, A.V.; Mackensen, A.; Schloss, I.R.; Barlett, E.R.; Jerosch, K.; Busso, A.S.; Abele, D. Anatomy of a glacial meltwater discharge event in an Antarctic cove. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170163. [Google Scholar] [CrossRef]
- Carroll, D.; Sutherland, D.A.; Hudson, B.; Moon, T.; Catania, G.A.; Shroyer, E.L.; Nash, J.D.; Bartholomaus, T.C.; Felikson, D.; Stearns, L.A.; et al. The impact of glacier geometry on meltwater plume structure and submarine melt in Greenland fjords. Geophys. Res. Lett. 2016, 43, 9739–9748. [Google Scholar] [CrossRef] [Green Version]
- Vernet, M.; Martinson, D.; Iannuzzi, R.; Stammerjohn, S.; Kozlowski, W.; Sines, K.; Smith, R.; Garibotti, I. Primary production within the sea-ice zone west of the Antarctic Peninsula: I—Sea ice, summer mixed layer, and irradiance. Deep Sea Res. Part II Top. Stud. Oceanogr. 2008, 55, 2068–2085. [Google Scholar] [CrossRef]
- Pan, B.J.; Vernet, M.; Reynolds, R.A.; Mitchell, B.G. The optical and biological properties of glacial meltwater in an Antarctic fjord. PLoS ONE 2019, 14, e0211107. [Google Scholar] [CrossRef] [Green Version]
- Straneo, F.; Cenedese, C. The dynamics of Greenland’s glacial fjords and their role in climate. Annu. Rev. Mar. Sci. 2015, 7, 89–112. [Google Scholar] [CrossRef]
- Fegel, T.S.; Baron, J.S.; Fountain, A.G.; Johnson, G.F.; Hall, E.K. The differing biogeochemical and microbial signatures of glaciers and rock glaciers. J. Geophys. Res. Biogeosciences 2016, 121, 919–932. [Google Scholar] [CrossRef] [Green Version]
- How, P.; Benn, D.I.; Hulton, N.R.; Hubbard, B.; Luckman, A.; Sevestre, H.; Van Pelt, W.; Lindbäck, K.; Kohler, J.; Boot, W. Rapidly changing subglacial hydrological pathways at a tidewater glacier revealed through simultaneous observations of water pressure, supraglacial lakes, meltwater plumes and surface velocities. Cryosphere 2017, 11, 2691–2710. [Google Scholar] [CrossRef] [Green Version]
- McGrath, D.; Steffen, K.; Overeem, I.; Mernild, S.H.; Hasholt, B.; Van Den Broeke, M. Sediment plumes as a proxy for local ice-sheet runoff in Kangerlussuaq Fjord, West Greenland. J. Glaciol. 2010, 56, 813–821. [Google Scholar] [CrossRef] [Green Version]
- Dierssen, H.M.; Smith, R.C.; Vernet, M. Glacial meltwater dynamics in coastal waters west of the Antarctic peninsula. Proc. Natl. Acad. Sci. USA 2002, 99, 1790–1795. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Truffer, M.; Motyka, R.J. Where glaciers meet water: Subaqueous melt and its relevance to glaciers in various settings. Rev. Geophys. 2016, 54, 220–239. [Google Scholar] [CrossRef] [Green Version]
- Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Pajuelo Madrigal, V.; Mallinis, G.; Ben-Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the use of unmanned aerial systems for environmental monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef] [Green Version]
- Whitehead, K.; Hugenholtz, C.H.; Myshak, S. Remote sensing of the environment with small unmanned aircraft systems (UASs), part 2: Scientific and commercial applications. J. Unmanned Veh. Syst. 2014, 2, 86–102. [Google Scholar] [CrossRef] [Green Version]
- Shahtahmassebi, A.; Yang, N.; Wang, K.; Moore, N.; Shen, Z. Review of shadow detection and de-shadowing methods in remote sensing. Chin. Geogr. Sci. 2013, 23, 403–420. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Zhang, G.; Yang, X.; Li, S.; Li, Y.; Wang, H.H. Single image shadow detection and removal based on feature fusion and multiple dictionary learning. Multimed. Tools Appl. 2018, 77, 18601–18624. [Google Scholar] [CrossRef]
- Liasis, G.; Stavrou, S. Satellite images analysis for shadow detection and building height estimation. ISPRS J. Photogramm. Remote Sens. 2016, 119, 437–450. [Google Scholar] [CrossRef]
- Sarabandi, P.; Yamazaki, F.; Matsuoka, M.; Kiremidjian, A. Shadow detection and radiometric restoration in satellite high resolution images. IEEE Int. Geosci. Remote Sens. Symp. 2004, 6, 3744–3747. [Google Scholar] [CrossRef]
- Wang, Q.; Yan, L.; Yuan, Q.; Ma, Z. An automatic shadow detection method for VHR remote sensing orthoimagery. Remote Sens. 2017, 9, 469. [Google Scholar] [CrossRef] [Green Version]
- Wu, S.T.; Hsieh, Y.T.; Chen, C.T.; Chen, J.C. A Comparison of 4 shadow compensation techniques for land cover classification of shaded areas from high radiometric resolution aerial images. Can. J. Remote Sens. 2014, 40, 315–326. [Google Scholar] [CrossRef]
- Yamazaki, F.; Liu, W.; Takasaki, M. Characteristics of shadow and removal of its effects for remote sensing imagery. IEEE Int. Geosci. Remote Sens. Symp. 2009, 4, 426. [Google Scholar] [CrossRef]
- França, M.M.; Fernandes Filho, E.I.; Ferreira, W.P.; Lani, J.L.; Soares, V.P. Topographic shadow influence on optical image acquired by satellite in the southern hemisphere. Eng. Agric. 2018, 38, 728–740. [Google Scholar] [CrossRef]
- Movia, A.; Beinat, A.; Crosilla, F. Shadow detection and removal in RGB VHR images for land use unsupervised classification. ISPRS J. Photogramm. Remote Sens. 2016, 119, 485–495. [Google Scholar] [CrossRef]
- Arévalo, V.; González, J.; Ambrosio, G. Shadow detection in colour high-resolution satellite images. Int. J. Remote Sens. 2008, 29, 1945–1963. [Google Scholar] [CrossRef]
- Qiao, X.; Yuan, D.; Li, H. Urban shadow detection and classification using hyperspectral image. J. Indian Soc. Remote Sens. 2017, 45, 945–952. [Google Scholar] [CrossRef]
- Tatar, N.; Saadatseresht, M.; Arefi, H.; Hadavand, A. A robust object-based shadow detection method for cloud-free high resolution satellite images over urban areas and water bodies. Adv. Space Res. 2018, 61, 2787–2800. [Google Scholar] [CrossRef]
- Yang, J.; He, Y.; Caspersen, J. Fully constrained linear spectral unmixing based global shadow compensation for high resolution satellite imagery of urban areas. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 88–98. [Google Scholar] [CrossRef]
- Aboutalebi, M.; Torres-Rua, A.F.; Kustas, W.P.; Nieto, H.; Coopmans, C.; McKee, M. Assessment of different methods for shadow detection in high-resolution optical imagery and evaluation of shadow impact on calculation of NDVI, and evapotranspiration. Irrig. Sci. 2019, 37, 407–429. [Google Scholar] [CrossRef]
- Poblete, T.; Ortega-Farías, S.; Ryu, D. Automatic coregistration algorithm to remove canopy shaded pixels in UAV-borne thermal images to improve the estimation of crop water stress index of a drip-irrigated Cabernet Sauvignon vineyard. Sensors 2018, 18, 397. [Google Scholar] [CrossRef] [Green Version]
- Tarko, A.; De Bruin, S.; Bregt, A.K. Comparison of manual and automated shadow detection on satellite imagery for agricultural land delineation. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 493–502. [Google Scholar] [CrossRef]
- Amin, R.; Gould, R.; Hou, W.; Arnone, R.; Lee, Z. Optical algorithm for cloud shadow detection over water. IEEE Trans. Geosci. Remote Sens. 2012, 51, 732–741. [Google Scholar] [CrossRef]
- Mostafa, Y.; Abdelhafiz, A. Shadow identification in high resolution satellite images in the presence of water regions. Photogramm. Eng. Remote Sens. 2017, 83, 87–94. [Google Scholar] [CrossRef]
- Xie, H.; Luo, X.; Xu, X.; Tong, X.; Jin, Y.; Pan, H.; Zhou, B. New hyperspectral difference water index for the extraction of urban water bodies by the use of airborne hyperspectral images. J. Appl. Remote Sens. 2014, 8, 085098. [Google Scholar] [CrossRef] [Green Version]
- Zeng, C.; Richardson, M.; King, D.J. The impacts of environmental variables on water reflectance measured using a lightweight unmanned aerial vehicle (UAV)-based spectrometer system. Isprs J. Photogramm. Remote Sens. 2017, 130, 217–230. [Google Scholar] [CrossRef]
- Amin, R.; Zhou, J.; Gilerson, A.; Gross, B.; Moshary, F.; Ahmed, S. Novel optical techniques for detecting and classifying toxic dinoflagellate Karenia brevis blooms using satellite imagery. Opt. Express 2009, 17, 9126–9144. [Google Scholar] [CrossRef]
- Rückamp, M.; Braun, M.; Suckro, S.; Blindow, N. Observed glacial changes on the King George Island ice cap, Antarctica, in the last decade. Glob. Planet. Chang. 2011, 79, 99–109. [Google Scholar] [CrossRef]
- Wójcik, K.A.; Bialik, R.J.; Osińska, M.; Figielski, M. Investigation of Sediment-Rich Glacial Meltwater Plumes Using a High-Resolution Multispectral Sensor Mounted on an Unmanned Aerial Vehicle. Water 2019, 11, 2405. [Google Scholar] [CrossRef] [Green Version]
- Gindraux, S.; Boesch, R.; Farinotti, D. Accuracy assessment of digital surface models from unmanned aerial vehicles’ imagery on glaciers. Remote Sens. 2017, 9, 186. [Google Scholar] [CrossRef] [Green Version]
- Jaud, M.; Passot, S.; Le Bivic, R.; Delacourt, C.; Grandjean, P.; Le Dantec, N. Assessing the accuracy of high resolution digital surface models computed by PhotoScan® and MicMac® in sub-optimal survey conditions. Remote Sens. 2016, 8, 465. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://desktop.arcgis.com/ (accessed on 22 December 2020).
- Novoa, S.; Doxaran, D.; Ody, A.; Vanhellemont, Q.; Lafon, V.; Lubac, B.; Gernez, P. Atmospheric corrections and multi-conditional algorithm for multi-sensor remote sensing of suspended particulate matter in low-to-high turbidity levels coastal waters. Remote Sens. 2017, 9, 61. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; He, G.; Wang, X. A practical DOS model-based atmospheric correction algorithm. Int. J. Remote Sens. 2010, 31, 2837–2852. [Google Scholar] [CrossRef]
- Mostafa, Y. A review on various shadow detection and compensation techniques in remote sensing images. Can. J. Remote Sens. 2017, 43, 545–562. [Google Scholar] [CrossRef]
- Montero, G.; Escobar, J.M.; Rodríguez, E.; Montenegro, R. Solar radiation and shadow modelling with adaptive triangular meshes. Sol. Energy 2009, 83, 998–1012. [Google Scholar] [CrossRef]
- Łupikasza, E.B.; Ignatiuk, D.; Grabiec, M.; Cielecka, K.; Laska, M.; Jania, J.A.; Luks, B.; Uszczyk, A.; Budzik, T. The Role of Winter Rain in the Glacial System on Svalbard. Water 2019, 11, 334. [Google Scholar] [CrossRef] [Green Version]
- Rachlewicz, G. Mid-winter thawing in the vicinity of Arctowski Station, King George Island. Pol. Polar Res. 1997, 18, 15–24. [Google Scholar]
- Gray, P.C.; Ridge, J.T.; Poulin, S.K.; Seymour, A.C.; Schwantes, A.M.; Swenson, J.J.; Johnston, D.W. Integrating drone imagery into high resolution satellite remote sensing assessments of estuarine environments. Remote Sens. 2018, 10, 1257. [Google Scholar] [CrossRef] [Green Version]
- Fu, H.; Zhou, T.; Sun, C. Object-Based Shadow Index via Illumination Intensity from High Resolution Satellite Images over Urban Areas. Sensors 2020, 20, 1077. [Google Scholar] [CrossRef] [Green Version]
- Doxaran, D.; Ruddick, K.; McKee, D.; Gentili, B.; Tailliez, D.; Chami, M.; Babin, M. Spectral variations of light scattering by marine particles in coastal waters, from the visible to the near infrared. Limnol. Oceanogr. 2009, 54, 1257–1271. [Google Scholar] [CrossRef] [Green Version]
- Dogliotti, A.I.; Ruddick, K.G.; Nechad, B.; Doxaran, D.; Knaeps, E. A single algorithm to retrieve turbidity from remotely-sensed data in all coastal and estuarine waters. Remote Sens. Environ. 2015, 156, 157–168. [Google Scholar] [CrossRef] [Green Version]
- Knaeps, E.; Ruddick, K.G.; Doxaran, D.; Dogliotti, A.I.; Nechad, B.; Raymaekers, D.; Sterckx, S. A SWIR based algorithm to retrieve total suspended matter in extremely turbid waters. Remote Sens. Environ. 2015, 168, 66–79. [Google Scholar] [CrossRef] [Green Version]
- Novo, E.M.M.; Hansom, J.D.; Curran, P.J. The effect of viewing geometry and wavelength on the relationship between reflectance and suspended sediment concentration. Int. J. Remote Sens. 1989, 10, 1357–1372. [Google Scholar] [CrossRef]
- Lynch, D.K. Shadows. Appl. Opt. 2015, 54, B154–B164. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; DiGiacomo, P.M. Uncertainties and applications of satellite-derived coastal water quality products. Prog. Oceanogr. 2017, 159, 45–72. [Google Scholar] [CrossRef]
- Mostafa, Y.; Abdelwahab, M.A. Corresponding regions for shadow restoration in satellite high-resolution images. Int. J. Remote Sens. 2018, 39, 7014–7028. [Google Scholar] [CrossRef]













| Glacier | Ecology | Zalewski | Dera | Ladies | Krak | Vieville | ||
|---|---|---|---|---|---|---|---|---|
| Inspire 2 Zenmuse X5 | ||||||||
| Area covered (km2) | 1.270 | 1.220 | 1.460 | 0.900 | 0.530 | 1.284 | ||
| Flight altitude (m) | 190 | 430 | 400 | 500 | 145 | 200 | ||
| Pixel resolution (cm) | 3.94 | 6.47 | 7.10 | 9.45 | 2.64 | 4.09 | ||
| RMSE X|Y|Z (m) | 3.1/3.3/2.5 | 3.0/3.1/1.2 | 3.0/3.0/1.2 | 3.1/3.3/1.4 | 3.6/3.5/0.8 | 3.2/4.3/1.0 | ||
| Mission date | 10 February 2019 | 21 Feuruary 2019 | 24 Feuruary 2019 | 6 November 2019 | 21 Feuruary 2019 | 15 Feuruary 2020 | ||
| Bluegrass Parrot Sequoia+ | ||||||||
| Area covered (km2) | - | 0.300 | 0.320 | 0.323 | - | - | 0.343 | - |
| Flight altitude (m) | - | 150 | 150 | 150 | - | - | 145 | - |
| Pixel resolution (cm) | - | 14.78 | 15.34 | 15.42 | - | - | 14.69 | - |
| Hour | - | 6:57–7:06 a.m. | 7:49–7:57 a.m. | 3:28–3:37 p.m. | - | - | 1:04–1:34 p.m. | - |
| Mission date | 31 January 2019 | 31 January 2019 | 9 March 2020 | 5 March 2019 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wójcik-Długoborska, K.A.; Bialik, R.J. The Influence of Shadow Effects on the Spectral Characteristics of Glacial Meltwater. Remote Sens. 2021, 13, 36. https://doi.org/10.3390/rs13010036
Wójcik-Długoborska KA, Bialik RJ. The Influence of Shadow Effects on the Spectral Characteristics of Glacial Meltwater. Remote Sensing. 2021; 13(1):36. https://doi.org/10.3390/rs13010036
Chicago/Turabian StyleWójcik-Długoborska, Kornelia Anna, and Robert Józef Bialik. 2021. "The Influence of Shadow Effects on the Spectral Characteristics of Glacial Meltwater" Remote Sensing 13, no. 1: 36. https://doi.org/10.3390/rs13010036
APA StyleWójcik-Długoborska, K. A., & Bialik, R. J. (2021). The Influence of Shadow Effects on the Spectral Characteristics of Glacial Meltwater. Remote Sensing, 13(1), 36. https://doi.org/10.3390/rs13010036