High-Resolution Coherency Functionals for Improving the Velocity Analysis of Ground-Penetrating Radar Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description and GPR Survey
2.2. High Coherency Functionals Rationale
3. Results
3.1. Velocity Analysis of the Synthetic Data
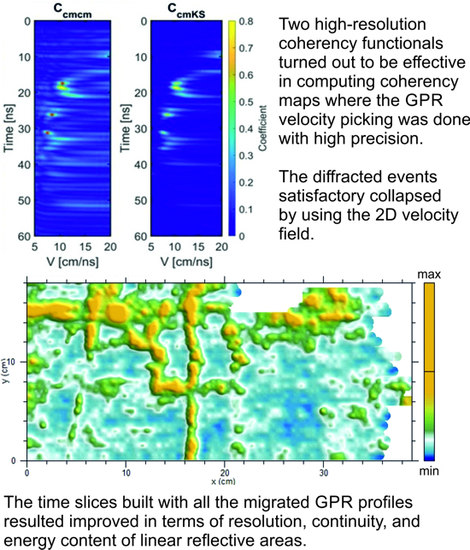
3.2. Velocity Analysis on the Real Data
3.3. The Effect of Varying Velocity Field on Time-slices
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Davis, J.L.; Annan, A.P. Ground Penetrating Radar for high resolution mapping of soil and rock stratigraphy. Geophys. Prospect. 1989, 37, 531–551. [Google Scholar] [CrossRef]
- Annan, A.P. Electromagnetic principles of ground penetrating radar. In Ground Penetrating Radar: Theory and Applications; Jol, H.M., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 3–40. [Google Scholar]
- Cassidy, N.J. Ground penetrating radar data processing, modelling and analysis. In Ground Penetrating Radar: Theory and Applications; Jol, H.M., Ed.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 141–176. [Google Scholar]
- Persico, R. Introduction to Ground Penetrating Radar. Inverse Scattering and Data Processing; IEEE Press Wiley: Hoboken, NJ, USA, 2014; p. 400. [Google Scholar]
- Allroggen, N.; Tronicke, J.; Delock, M.; Böniger, U. Topographic migration of 2D and 3D ground-penetrating radar data considering variable velocities. Near Surf. Geophys. 2015, 13, 253–259. [Google Scholar] [CrossRef]
- Neidell, N.S.; Taner, M.T. Semblance and other coherency measures for multichannel data. Geophysics 1971, 36, 482–497. [Google Scholar] [CrossRef]
- Maas, C.; Schmalzl, J. Using pattern recognition to automatically localize reflection hyperbolas in data from ground penetrating radar. Comput. Geosci. 2013, 58, 116–125. [Google Scholar] [CrossRef]
- Laurence, M.; Persico, R.; Matera, L.; Lambot, S. Automated Detection of Reflection Hyperbolas in Complex GPR Images with no a priori knowledge on the medium. IEEE Trans. Geosci. Remote Sens. 2016, 54, 580–596. [Google Scholar]
- Ribolini, A.; Bini, M.; Isola, I.; Coschino, F.; Baroni, C.; Salvatore, M.C.; Zanchetta, G.; Fornaciari, A. GPR versus Geoarchaeological Findings in a Complex Archaeological Site (Badia Pozzeveri, Italy). Arch. Prosp. 2017, 24, 141–156. [Google Scholar] [CrossRef]
- Sguazzero, P.; Vesnaver, A. A comparative analysis of algorithms for seismic velocity estimation. In Deconvolution and Inversion; Bernabini, M., Rocca, F., Treitel, S., Worthington, M., Eds.; Blackwell: London, UK, 1987; pp. 267–286. [Google Scholar]
- Key, S.C.; Smithson, S.B. New approach to seismic-reflection event detection and velocity determination. Geophysics 1990, 55, 1057–1069. [Google Scholar] [CrossRef]
- Grion, S.; Mazzotti, A.; Spagnolini, U. Joint estimation of AVO and kinematics parameters. Geophys. Prospect. 1998, 46, 405–422. [Google Scholar] [CrossRef]
- Sacchi, M.D. A bootstrap procedure for high-resolution velocity analysis. Geophysics 1998, 63, 1716–1725. [Google Scholar] [CrossRef]
- Grandi, A.; Stucchi, E.; Mazzotti., A. Multicomponent velocity analysis by means of covariance measures and complex matched filters. In Proceedings of the 74th Annual International Meeting, Denver, CO, USA, 10–14 October 2004; Society of Exploration Geophysicists: Huston, TX, USA, 2004; pp. 2415–2418. [Google Scholar]
- Grandi, A.; Mazzotti, A.; Stucchi, E. Multicomponent velocity analysis with quaternions. Geophys. Prospect. 2007, 55, 761–777. [Google Scholar] [CrossRef]
- Abbad, B.; Ursin, B. High-resolution bootstrapped differential semblance. Geophysics 2012, 77, U39–U47. [Google Scholar] [CrossRef]
- Tognarelli, A.; Stucchi, E.; Ravasio, A.; Mazzotti, A. High-resolution coherency functionals for velocity analysis: An application for subbasalt seismic exploration. Geophysics 2013, 78, U53–U63. [Google Scholar] [CrossRef] [Green Version]
- Gong, X.; Wang, S.; Zhang, T. Velocity analysis using high-resolution semblance based on sparse hyperbolic Radon transform. J. Appl. Geophys. 2016, 134, 146–152. [Google Scholar] [CrossRef]
- Goodman, D.; Nishimura, Y.; Rogers, J.D. GPR timeslices in archaeological prospection. Archaeol. Prospect. 1995, 2, 85–89. [Google Scholar]
- Nuzzo, L.; Leucci, G.; Negri, S.; Carrozzo, M.T.; Quarta, T. Application of 3D visualization techniques in the analysis of GPR data for archaeology. Ann. Geophys. 2002, 45, 321–337. [Google Scholar]
- Leckebush, J. Ground-penetrating radar: A modern three-dimensional prospection method. Archaeol. Prospect. 2003, 10, 213–240. [Google Scholar] [CrossRef]
- Grasmueck, M.; Weger, R.; Horstmeyer, H. Three-dimensional ground-penetrating radar imaging of sedimentary structures, fractures, and archaeological features at submeter resolution. Geology 2004, 32, 933–936. [Google Scholar] [CrossRef]
- Soldovieri, F.; Orlando, L. Novel tomographic based approach and processing strategies for GPR measurements using multifrequency antennas. J. Cult. Herit. 2009, 10, 83–92. [Google Scholar] [CrossRef]
- Bini, M.; Fornaciari, A.; Ribolini, A.; Bianchi, A.; Sartini, S.; Coschino, F. Medieval phases of settlement at Benabbio castle, Apennine Mountains, Italy: Evidence from ground penetrating radar survey. J. Archaeol. Sci. 2010, 37, 3059–3067. [Google Scholar] [CrossRef]
- Tinelli, C.; Ribolini, A.; Bianucci, G.; Bini, M.; Landini, W. Ground penetrating radar and palaeontology: The detection of sirenian fossil bones under a sunflower field in Tuscany (Italy). Comptes Rendus Palevol 2012, 11, 445–454. [Google Scholar] [CrossRef]
- Fornaciari, A. Badia Pozzeveri. Dalla terra alla storia. LUK 2014, 20, 30–36. [Google Scholar]
- IDS GeoRadar. Available online: https://idsgeoradar.com/ (accessed on 12 May 2020).
- Spagnolini, U.; Maciotta, L.; Manni, A. Velocity analysis by truncated singular value decomposition. In Proceedings of the 63rd Annual International Meeting, Washington, DC, USA, 26–30 September 1993; Society of Exploration Geophysicists: Huston, TX, USA; pp. 677–680. [Google Scholar]
- Tognarelli, A.; Aleardi, M.; Mazzotti, A. Estimation of a high resolution P-wave velocity model of the seabed layers by means of global and a gradient-based FWI. In Proceedings of the Second Applied Shallow Marine Geophysics Conference, Barcelon, Spain, 4–8 September 2016; European Association of Geosciences and Engineering. [Google Scholar] [CrossRef]
- Geophysical Archaeometry Laboratory. Available online: https://www.gpr-survey.com/ (accessed on 12 May 2020).
- Goodman, D. Ground-penetrating radar simulation in engineering and archaeology. Geophysics 1994, 59, 224–232. [Google Scholar] [CrossRef]
- Yilmaz, O. Seismic Data Analysis: I—Processing, Inversion, and Interpretation of Seismic Data; Doherty, S.M., Ed.; Society of Exploration Geophysics: Tulsa, OK, USA, 2001; p. 2065. [Google Scholar]











| n | 64 | Number of Time Samples of the Velocity Analysis Window |
|---|---|---|
| win_ap | 101 | Aperture of the velocity analysis window (number of traces) |
| v | 4–20 | Velocity interval scanned by velocity analysis (cm/ns) |
| dv | 0.1 | Increment in the velocity scanned (cm/ns) |
| dt0 | 0.098 | Time increment in the functional computation (ns) |
| noise | 0.1 | Standard deviation of the added white noise to avoid functional singularity |
| wavelet | 600 MHz | Maximum of the Ricker wavelet frequency spectrum |
| n | 64 | Number of Time Samples of the Velocity Analysis Window |
|---|---|---|
| win_ap | 81 | Aperture of the velocity analysis window (number of traces) |
| v | 4–20 | Velocity interval scanned by velocity analysis (cm/ns) |
| dv | 0.1 | Increment in the velocity scanned (cm/ns) |
| dt0 | 0.098 | Time increment in the functional computation (ns) |
| wavelet | 400 MHz | Maximum of the Ricker wavelet frequency spectrum |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stucchi, E.; Ribolini, A.; Tognarelli, A. High-Resolution Coherency Functionals for Improving the Velocity Analysis of Ground-Penetrating Radar Data. Remote Sens. 2020, 12, 2146. https://doi.org/10.3390/rs12132146
Stucchi E, Ribolini A, Tognarelli A. High-Resolution Coherency Functionals for Improving the Velocity Analysis of Ground-Penetrating Radar Data. Remote Sensing. 2020; 12(13):2146. https://doi.org/10.3390/rs12132146
Chicago/Turabian StyleStucchi, Eusebio, Adriano Ribolini, and Andrea Tognarelli. 2020. "High-Resolution Coherency Functionals for Improving the Velocity Analysis of Ground-Penetrating Radar Data" Remote Sensing 12, no. 13: 2146. https://doi.org/10.3390/rs12132146
APA StyleStucchi, E., Ribolini, A., & Tognarelli, A. (2020). High-Resolution Coherency Functionals for Improving the Velocity Analysis of Ground-Penetrating Radar Data. Remote Sensing, 12(13), 2146. https://doi.org/10.3390/rs12132146