Combining Multi-Source Data and Machine Learning Approaches to Predict Winter Wheat Yield in the Conterminous United States
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Acquisition and Preprocessing
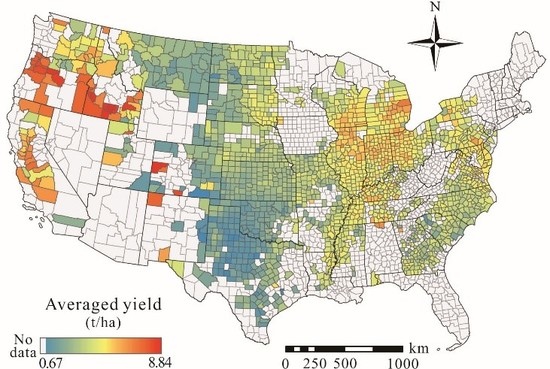
2.1.1. Wheat Yield Data
2.1.2. VI Data
2.1.3. Climate Data
2.1.4. Soil Data
2.1.5. Data Preprocessing
2.2. Model Development and Performance Evaluation
2.2.1. Strategy for Input Variable Selection
2.2.2. Machine Learning Algorithms for Yield Prediction
2.2.3. Metrics for Model Evaluation
3. Results
3.1. Important Factor Selection.
3.2. Model Comparison
3.3. The Spatial Patterns of Predicted Yield
3.4. Multi-Source Data Contribution
3.5. Time-Series Prediction Performance
4. Discussion
4.1. Performance of Machine Learning Models
4.2. Spatial Adaptability of Model Performance
4.3. Impact of Multi-Source Data on Yield Prediction
4.4. Uncertainties and Future Work
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A


| ES | MS | ES + MS | LS | MS + LS | ES + MS + LS | |
|---|---|---|---|---|---|---|
| VI | 0.468 | 0.492 | 0.587 | 0.709 | 0.714 | 0.727 |
| Climate | 0.312 | 0.486 | 0.578 | 0.607 | 0.671 | 0.692 |
| VI + Climate | 0.496 | 0.644 | 0.678 | 0.742 | 0.756 | 0.760 |
References
- FAO. World Food and Agriculture Statistical Pocketbook; FAO: Rome, Italy, 2019. [Google Scholar]
- FAO. FAOSTAT. Available online: http://www.fao.org/faostat/zh/#data/QC (accessed on 2 December 2019).
- Lesk, C.; Rowhani, P.; Ramankutty, N. Influence of extreme weather disasters on global crop production. Nature 2016, 529, 84–87. [Google Scholar] [CrossRef] [PubMed]
- Franch, B.; Vermote, E.F.; Becker–Reshef, I.; Claverie, M.; Huang, J.; Zhang, J.; Justice, C.; Sobrino, J.A. Improving the timeliness of winter wheat production forecast in the United States of America, Ukraine and China using MODIS data and NCAR Growing Degree Day information. Remote Sens. Environ. 2015, 161, 131–148. [Google Scholar] [CrossRef]
- Statista. U.S. Imports and Exports of Wheat from 2000/01 to 2018/19 (in Million Metric Tons). Available online: https://www.statista.com/statistics/237902/us–wheat–imports–and–exports–since–2000/ (accessed on 2 December 2019).
- USDA. Wheat Sector at a Glance. Available online: https://www.ers.usda.gov/topics/crops/cotton-wool/cotton-sector-at-a-glance/ (accessed on 2 December 2019).
- Rembold, F.; Atzberger, C.; Savin, I.; Rojas, O. Using low resolution satellite imagery for yield prediction and yield anomaly detection. Remote Sens. 2013, 5, 1704–1733. [Google Scholar] [CrossRef] [Green Version]
- Sibley, A.M.; Grassini, P.; Thomas, N.E.; Cassman, K.G. Testing remote sensing approaches for assessing yield variability among maize fields. Agron. J. 2014, 106, 24–32. [Google Scholar] [CrossRef]
- Guan, K.Y.; Wu, J.; Kimball, J.S.; Anderson, M.C.; Frolking, S.; Li, B.; Hain, C.R.; Lobe, D.B. The shared and unique values of optical, fluorescence, thermal and microwave satellite data for estimating large–scale crop yields. Remote Sens. Environ. 2017, 199, 333–349. [Google Scholar] [CrossRef] [Green Version]
- Kayad, A.G.; Al-Gaadi, K.A.; Tola, E.; Madugundu, R.; Zeyada, A.M.; Kalaitzidis, C. Assessing the spatial variability of alfalfa yield using satellite imagery and ground–based data. PLoS ONE 2016, 11. [Google Scholar] [CrossRef]
- Ren, J.; Chen, Z.; Zhou, Q.; Tang, H. Regional yield estimation for winter wheat with MODIS–NDVI data in Shandong, China. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 403–413. [Google Scholar] [CrossRef]
- Becker–Reshef, I.; Vermote, E.; Lindeman, M.; Justice, C. A generalized regression–based model for forecasting winter wheat yields in Kansas and Ukraine using MODIS data. Remote Sens. Environ. 2010, 114, 1312–1323. [Google Scholar] [CrossRef]
- Kouadio, L.; Newlands, K.N.; Davidson, A.; Zhang, Y.; Chipanshi, A. Assessing the Performance of MODIS NDVI and EVI for Seasonal Crop Yield Forecasting at the Ecodistrict Scale. Remote Sens. 2014, 6, 10193–10214. [Google Scholar] [CrossRef] [Green Version]
- Holzman, M.E.; Rivas, R.; Piccolo, M.C. Estimating soil moisture and the relationship with crop yield using surface temperature and vegetation index. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 181–192. [Google Scholar] [CrossRef]
- Balaghi, R.; Tychon, B.; Eerens, H.; Jlibene, M. Empirical regression models using NDVI, rainfall and temperature data for the early prediction of wheat grain yields in Morocco. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 438–452. [Google Scholar] [CrossRef] [Green Version]
- Newlands, N.K.; Zamar, D.S.; Kouadio, L.A.; Zhang, Y.; Chipanshi, A.; Potgieter, A.; Toure, S.; Hill, H.S.J. An integrated, probabilistic model for improved seasonal forecasting of agricultural crop yield under environmental uncertainty. Front. Environ. Sci. 2014, 2, 17. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Kang, Y.; Ozdogan, M.; Zhang, Z. County–Level Corn Yield Prediction Using Deep Transfer Learning. In Proceedings of the AGU Fall Meeting 2019, San Francisco, CA, USA, 9–13 December 2019. [Google Scholar]
- Saeed, U.; Dempewolf, J.; Becker–Reshef, I.; Khan, A.; Ahmad, A.; Wajid, S.A. Forecasting wheat yield from weather data and MODIS NDVI using Random Forests for Punjab province, Pakistan. Int. J. Remote Sens. 2017, 38, 4831–4854. [Google Scholar] [CrossRef]
- Cai, Y.; Guan, K.; Lobell, D.; Potgieter, A.B.; Wang, S.; Peng, J.; Xu, T.; Asseng, S.; Zhang, Y.; You, L.; et al. Integrating satellite and climate data to predict wheat yield in Australia using machine learning approaches. Agric. For. Meteorol. 2019, 274, 144–159. [Google Scholar] [CrossRef]
- Zhang, Z.; Jin, Y.; Chen, B.; Brown, P. California Almond Yield Prediction at the Orchard Level With a Machine Learning Approach. Front. Plant Sci. 2019, 10, 809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ritchie, J.T.O. Description and performance of CERES wheat: A user—Oriented wheat yield model. ARS Wheat Yield Proj. 1985, 159–175. [Google Scholar]
- Jamieson, P.D.; Porter, J.R.; Wilson, D.R. A test of the computer simulation model ARCWHEAT1 on wheat crops grown in New Zealand. Field Crop. Res. 1991, 27, 337–350. [Google Scholar] [CrossRef]
- Hansen, S.; Jensen, H.E.; Nielsen, N.E.; Svendsen, H. Simulation of nitrogen dynamics and biomass production in winter wheat using the Danish simulation model DAISY. Fertil. Res. 1991, 27, 245–259. [Google Scholar] [CrossRef]
- Jamieson, P.D.; Semenov, M.A.; Brooking, I.R.; Francis, G.S. Sirius: A mechanistic model of wheat response to environmental variation. Eur. J. Agron. 1998, 8, 161–179. [Google Scholar] [CrossRef]
- Porter, J.R. AFRCWHEAT2: A model of the growth and development of wheat incorporating responses to water and nitrogen. Eur. J. Agron. 1993, 2, 69–82. [Google Scholar] [CrossRef]
- Moriondo, M.; Maselli, F.; Bindi, M. A simple model of regional wheat yield based on NDVI data. Eur. J. Agron. 2007, 26, 266–274. [Google Scholar] [CrossRef]
- Lobell, D.B.; Burke, M.B. On the use of statistical models to predict crop yield responses to climate change. Agric. For. Meteorol. 2010, 150, 1443–1452. [Google Scholar] [CrossRef]
- Wall, L.; Larocque, D.; Léger, P.M. The early explanatory power of NDVI in crop yield modelling. Int. J. Remote Sens. 2008, 29, 2211–2225. [Google Scholar] [CrossRef]
- Dubey, R.P.; Ajwani, N.; Kalubarme, M.H.; Sridhar, V.N.; Navalgund, R.R.; Mahey, R.K.; Sidhu, S.S.; Jhorar, O.P.; Cheema, S.S.; Na Rang, R.S. Pre–harvest wheat yield and production estimation for the Punjab, India. Int. J. Remote Sens. 1994, 15, 2137–2144. [Google Scholar] [CrossRef]
- Sridhar, V.N.; Dadhwal, V.K.; Chaudhari, K.N.; Sharma, R.; Bairagi, G.D.; Sharma, A.K. Wheat production forecasting for a predominantly unirrigated region in Madhya Pradesh. Titleremote Sens. 1994, 15, 1307–1316. [Google Scholar] [CrossRef]
- Forecasting, Y. Analysis of GAC NDVI data for cropland identification and yield forecasting in Mediterranean African countries. Photogramm. Eng. Remote Sens. 2001, 67, 593–602. [Google Scholar]
- Doraiswamy, P.C.; Moulin, S.; Cook, P.W.; Stern, A. Crop yield assessment from remote sensing. Photogramm. Eng. Remote Sens. 2003, 69, 665–674. [Google Scholar] [CrossRef]
- Heremans, S.; Dong, Q.; Zhang, B.; Bydekerke, L.; Van Orshoven, J. Potential of ensemble tree methods for early–season prediction of winter wheat yield from short time series of remotely sensed normalized difference vegetation index and in situ meteorological data. J. Appl. Remote Sens. 2015, 9. [Google Scholar] [CrossRef]
- Zhang, Y.; Qin, Q.; Ren, H.; Sun, Y.; Li, M.; Zhang, T.; Ren, S. Optimal Hyperspectral Characteristics Determination for Winter Wheat Yield Prediction. Remote Sens. 2018, 10, 2015. [Google Scholar] [CrossRef] [Green Version]
- Safa, M.; Samarasinghe, S.; Nejat, M. Prediction of wheat production using artificial neural networks and investigating indirect factors affecting it: Case study in Canterbury province, New Zealand. J. Agric. Sci. Technol. 2015, 17, 791–803. [Google Scholar]
- Wang, L.A.; Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop J. 2016, 4, 212–219. [Google Scholar] [CrossRef] [Green Version]
- NASS. NASS Quick Stats. In USDA National Agricultural Statistics Service (NASS). Available online: http://quickstats.nass.usda.gov/ (accessed on 8 December 2019).
- USDA–NASS. Field Crops: Usual Planting and Harvesting Dates. In USDA National Agricultural Statistics Service, Agriculural Handbook; NASS: Burr Ridge, IL, USA, 2010. [Google Scholar]
- Miller, T.D. Growth Stages of Wheat: Identification and Understanding Improve Crop Management. Better Crops 1992, 76, 12–17. [Google Scholar]
- Son, N.T.; Chen, C.F.; Chen, C.R.; Minh, V.Q.; Trung, N.H. A comparative analysis of multitemporal MODIS EVI and NDVI data for large–scale rice yield estimation. Agric. For. Meteorol. 2014, 197, 52–64. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Peng, Y.; Gitelson, A.A. Application of chlorophyll–related vegetation indices for remote estimation of maize productivity. Agric. For. Meteorol. 2011, 151, 1267–1276. [Google Scholar] [CrossRef]
- Schaaf, C.; Wang, Z. MCD43A3 MODIS/Terra+ Aqua BRDF/Albedo Daily L3 Global—500 m V006; NASA: Washington, DC, USA, 2015.
- Gitelson, A.A.; Vina, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Niu, Z.; Gao, S. The potential of the satellite derived green chlorophyll index for estimating midday light use efficiency in maize, coniferous forest and grassland. Ecol. Indic. 2012, 14, 66–73. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.; Didan, K.; Miura, T. Development of a two–band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- PRISM. Climate Group; Oregon State University: Corvallis, OR, USA, 2019. [Google Scholar]
- Wan, Z.; Hook, S.; Hulley, G. MOD11A2 MODIS/Terra Land Surface Temperature/Emissivity 8–day L3 Global 1 km SIN Grid V006; LP DAAC: Sioux Falls, SD, USA, 2015.
- Ramcharan, A.; Hengl, T.; Nauman, T.; Brungard, C.; Waltman, S.; Wills, S.; Thompson, J. Soil Property and Class Maps of the Conterminous United States at 100–Meter Spatial Resolution. Soil Sci. Soc. Am. J. 2018, 82. [Google Scholar] [CrossRef] [Green Version]
- Thorup–Kristensen, K.; Salmerón Cortasa, M.; Loges, R. Winter wheat roots grow twice as deep as spring wheat roots, is this important for N uptake and N leaching losses? Plant Soil 2009, 322, 101–114. [Google Scholar] [CrossRef]
- USDA–NASS. USDA National Agricultural Statistics Service Cropland Data Layer. Available online: https://nassgeodata.gmu.edu/CropScape/ (accessed on 8 December 2019).
- Boryan, C.; Yang, Z.; Mueller, R.; Craig, M. Monitoring US agriculture: The US department of agriculture, national agricultural statistics service, cropland data layer program. Geocarto Int. 2011, 26, 341–358. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary–scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Evans, J.D. Straightforward Statistics for the Behavioral Sciences; Thomson Brooks/Cole Publishing Co: Three Lakes, WI, USA, 1996. [Google Scholar]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J. API design for machine learning software: Experiences from the scikit–learn project. arXiv 2013, arXiv:1309.0238. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Gunn, S.R. Support vector machines for classification and regression. ISIS Tech. Rep. 1998, 14, 5–16. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L.J.M.l. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Sinha, P.; Gaughan, A.E.; Stevens, F.R.; Nieves, J.J.; Sorichetta, A.; Tatem, A.J. Assessing the spatial sensitivity of a random forest model: Application in gridded population modeling. Comput. Environ. Urban Syst. 2019, 75, 132–145. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, X.; Chen, Z.; Ren, F.; Feng, L.; Du, Q. Optimizing the Predictive Ability of Machine Learning Methods for Landslide Susceptibility Mapping Using SMOTE for Lishui City in Zhejiang Province, China. Int. J. Environ. Res. Public Health 2019, 16, 368. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y.; Schapire, R.E. A decision–theoretic generalization of on–line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Zhong, L.; Hu, L.; Zhou, H. Deep learning based multi–temporal crop classification. Remote Sens. Environ. 2019, 221, 430–443. [Google Scholar] [CrossRef]
- Biganzoli, E.; Boracchi, P.; Mariani, L.; Marubini, E. Feed forward neural networks for the analysis of censored survival data: A partial logistic regression approach. Stat. Med. 1998, 17, 1169–1186. [Google Scholar] [CrossRef]
- Rojas, R. Neural Networks: A Systematic Introduction; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Peralta, N.; Assefa, Y.; Du, J.; Barden, C.; Ciampitti, I. Mid–season high–resolution satellite imagery for forecasting site–specific corn yield. Remote Sens. 2016, 8, 848. [Google Scholar] [CrossRef] [Green Version]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Hartling, S.; Esposito, F.; Fritschi, F.B. Soybean yield prediction from UAV using multimodal data fusion and deep learning. Remote Sens. Environ. 2020, 237. [Google Scholar] [CrossRef]
- Imran, M.; Stein, A.; Zurita–Milla, R. Using geographically weighted regression kriging for crop yield mapping in West Africa. Int. J. Geogr. Inf. Sci. 2015, 29, 234–257. [Google Scholar] [CrossRef]
- Cai, R.; Yu, D.; Oppenheimer, M. Estimating the Spatially Varying Responses of Corn Yields toWeather Variations using GeographicallyWeighted Panel Regression. J. Agric. Resour. Econ. 2014, 39, 230–252. [Google Scholar]
- Moran, P.A.P. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Ghulam, A.; Sandoval, J.S.O.; Maimaitiyiming, M. Drivers of land cover and land use changes in St. Louis metropolitan area over the past 40 years characterized by remote sensing and census population data. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 161–174. [Google Scholar] [CrossRef]
- Herbek, J.; Lee, C. A Comprehensive Guide to Wheat Management in Kentucky; University of Kentucky: Lexington, KY, USA, 2009. [Google Scholar]
- Wu, X.; Liu, H.; Li, X.; Tian, Y.; Mahecha, M.D. Responses of Winter Wheat Yields to Warming–Mediated Vernalization Variations Across Temperate Europe. Front. Ecol. Evol. 2017, 5, 126. [Google Scholar] [CrossRef] [Green Version]
- Fontana, D.C.; Potgieter, A.B.; Apan, A. Assessing the relationship between shire winter crop yield and seasonal variability of the MODIS NDVI and EVI images. Appl. GIS 2007, 3, 1–16. [Google Scholar]
- Labus, M.P.; Nielsen, G.A.; Lawrence, R.L.; Engel, R.; Long, D.S. Wheat yield estimates using multi–temporal NDVI satellite imagery. Int. J. Remote Sens. 2002, 23, 4169–4180. [Google Scholar] [CrossRef]
- Slafer, G.A.; Savin, R. Developmental base temperature in different phenological phases of wheat (Triticum aestivum). J. Exp. Bot. 1991, 42, 1077–1082. [Google Scholar] [CrossRef]
- Garg, D.; Sareen, S.; Dalal, S.; Tiwari, R.; Singh, R. Grain filling duration and temperature pattern influence on the performance of wheat genotypes under late planting. Cereal Res. Commun. 2013, 41, 500–507. [Google Scholar] [CrossRef]
- Feng, L.; Li, Y.; Wang, Y.; Du, Q. Estimating hourly and continuous ground–level PM2. 5 concentrations using an ensemble learning algorithm: The ST–stacking model. Atmos. Environ. 2019, 223, 117242. [Google Scholar] [CrossRef]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Kang, H.-W.; Kang, H.-B. Prediction of crime occurrence from multi–modal data using deep learning. PLoS ONE 2017, 12, e0176244. [Google Scholar] [CrossRef]
- Zhang, N.; Rao, R.S.P.; Salvato, F.; Havelund, J.F.; Møller, I.M.; Thelen, J.J.; Xu, D. MU–LOC: A machine–learning method for predicting mitochondrially localized proteins in plants. Front. Plant Sci. 2018, 9, 634. [Google Scholar] [CrossRef] [Green Version]
- Borchani, H.; Varando, G.; Bielza, C.; Larrañaga, P. A survey on multi-output regression. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2015, 5, 216–233. [Google Scholar] [CrossRef] [Green Version]
- Vergara–Díaz, O.; Zaman–Allah, M.A.; Masuka, B.; Hornero, A.; Zarco–Tejada, P.; Prasanna, B.M.; Cairns, J.E.; Araus, J.L. A novel remote sensing approach for prediction of maize yield under different conditions of nitrogen fertilization. Front. Plant Sci. 2016, 7, 666. [Google Scholar] [CrossRef] [Green Version]
- Tao, F.; Xiao, D.; Zhang, S.; Zhang, Z.; Rötter, R.P. Wheat yield benefited from increases in minimum temperature in the Huang–Huai–Hai Plain of China in the past three decades. Agric. For. Meteorol. 2017, 239, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Lobell, D.B. Assessing the heterogeneity and persistence of farmers’ maize yield performance across the North China Plain. Field Crop. Res. 2017, 205, 55–66. [Google Scholar] [CrossRef]
- Nawar, S.; Buddenbaum, H.; Hill, J.; Kozak, J. Modeling and mapping of soil salinity with reflectance spectroscopy and landsat data using two quantitative methods (PLSR and MARS). Remote Sens. 2014, 6, 10813–10834. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Ding, J.; Abulimiti, A.; Cai, L. Quantitative estimation of soil salinity by means of different modeling methods and visible–near infrared (VIS–NIR) spectroscopy, Ebinur Lake Wetland, Northwest China. PeerJ 2018, 6, e4703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Majchrzak, R.N.; Olson, K.R.; Bollero, G.; Nafziger, E.D. Using soil properties to predict wheat yields on Illinois soils. Soil Sci. 2001, 166, 267–280. [Google Scholar] [CrossRef]
- De La Rosa, D.; Cardona, F.; Almorza, J. Crop yield predictions based on properties of soils in Sevilla, Spain. Geoderma 1981, 25, 267–274. [Google Scholar] [CrossRef]








| Category | Variable Name | Spatial Resolution | Temporal Resolution | Time Coverage | Source |
|---|---|---|---|---|---|
| Crop data | Yield (t/ha) | County-level | Yearly | 2006–2018 | USDA NASS |
| Crop map | 30 m | Yearly | 2008–2018 | USDA NASS | |
| VIs | EVI | 500 m | Daily | 2007–2018 | MODIS |
| NDVI | |||||
| NDWI | |||||
| GCI | |||||
| Climate | LST_N (K) | 1 km | 8-day | 2007–2018 | MODIS |
| LST_D (K) | |||||
| TDmean (°C) | 4 km | Daily | 2007–2018 | PRISM | |
| Tmean (°C) | |||||
| Tmx (°C) | |||||
| Tmn (°C) | |||||
| VPDmx (hPa) | |||||
| VPDmn (hPa) | |||||
| PPT (mm) | |||||
| Soil | SOC (%) | 100 m | Static | 2017 | Soil Properties and Class 100 m Grids United States |
| CC (%) | |||||
| SC (%) | |||||
| TN (%) | |||||
| BD (g cm−3) | |||||
| PH |
| Factors | Model | RMSE | R2 | MAE |
|---|---|---|---|---|
| Full factors | OLS | 0.66 | 0.76 | 0.51 |
| LASSO | 0.69 | 0.75 | 0.54 | |
| SVM | 0.61 | 0.80 | 0.48 | |
| RF | 0.59 | 0.81 | 0.46 | |
| AdaBoost | 0.52 | 0.85 | 0.41 | |
| DNN | 0.64 | 0.78 | 0.51 | |
| Selected factors | OLS | 0.68 | 0.75 | 0.54 |
| LASSO | 0.57 | 0.81 | 0.45 | |
| SVM | 0.59 | 0.82 | 0.45 | |
| RF | 0.54 | 0.85 | 0.41 | |
| AdaBoost | 0.51 | 0.86 | 0.39 | |
| DNN | 0.62 | 0.83 | 0.49 |
| AdaBoost | RF | DNN | SVM | LASSO | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MI | P | MI | P | MI | P | MI | P | MI | P | |
| 2017 | 0.36 | 0.00 | 0.37 | 0.00 | 0.44 | 0.00 | 0.38 | 0.00 | 0.41 | 0.00 |
| 2018 | 0.32 | 0.00 | 0.33 | 0.00 | 0.34 | 0.00 | 0.34 | 0.00 | 0.53 | 0.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, Z.; Feng, L.; Du, Q.; Runge, T. Combining Multi-Source Data and Machine Learning Approaches to Predict Winter Wheat Yield in the Conterminous United States. Remote Sens. 2020, 12, 1232. https://doi.org/10.3390/rs12081232
Wang Y, Zhang Z, Feng L, Du Q, Runge T. Combining Multi-Source Data and Machine Learning Approaches to Predict Winter Wheat Yield in the Conterminous United States. Remote Sensing. 2020; 12(8):1232. https://doi.org/10.3390/rs12081232
Chicago/Turabian StyleWang, Yumiao, Zhou Zhang, Luwei Feng, Qingyun Du, and Troy Runge. 2020. "Combining Multi-Source Data and Machine Learning Approaches to Predict Winter Wheat Yield in the Conterminous United States" Remote Sensing 12, no. 8: 1232. https://doi.org/10.3390/rs12081232
APA StyleWang, Y., Zhang, Z., Feng, L., Du, Q., & Runge, T. (2020). Combining Multi-Source Data and Machine Learning Approaches to Predict Winter Wheat Yield in the Conterminous United States. Remote Sensing, 12(8), 1232. https://doi.org/10.3390/rs12081232