Real-Time Uncertainty Specification of All Sky Imager Derived Irradiance Nowcasts
Abstract
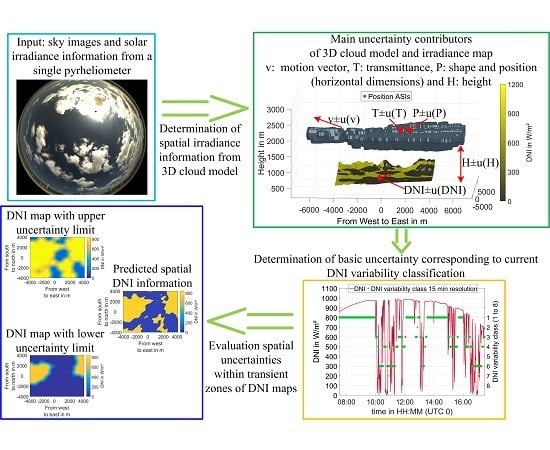
:1. Introduction
2. Materials
3. Methods and Results
3.1. Temporal DNI Variability Classes
- Class 1 describes clear sky conditions.
- Classes 2 and 3 describe nearly clear sky conditions with a stronger variability and comparatively lower average DNI in the case of class 3.
- Class 4 shows a strong temporal variability but with an overall high average DNI.
- Class 5 describes less variable conditions with a lower average DNI compared to class 4.
- Class 6 resembles class 4 with a strong temporal variability, but with a significantly lower average DNI.
- Class 7 describes nearly complete overcast situations with some ramps.
- Class 8 corresponds to overcast situations.
3.2. Weather Dependent Uncertainty Specification
3.2.1. Determination of Uncertainties
3.2.2. Real-Time Uncertainty Assessment of Spatial DNI Maps
- The basic uncertainties corresponding to the DNI variability class, Sun elevation angle, and lead time are added to the DNI map –taking the previously described physical boundaries into account.
- The DNI map is converted into a binary map (true = shaded). The expected uncertainty of the cloud shadow edge position is used as the width to dilate (lower uncertainty range) and erode (upper uncertainty range) the shaded part of the binary map [40]. The used morphological filters are based on the intrinsic MATLAB® functions imdilate and imerode.
- The transient and stable zones of the DNI maps are detected by comparing the original binary map to the binary maps treated by the morphological filters. All pixels with a changed status are part of the transient zone.
- Final DNI maps with uncertainty are created by a linear 2-D interpolation between shaded and clear areas, which are only within the transient zones.
3.2.3. Final Adjustments and Validation
3.3. Nowcast Uncertainties at Different Geographical Locations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. DNI Variability Classification Comparison Between Point Measurements and Field Averages

Appendix B. Comparison from p68.3 Values within Distinct Sun Elevation Angle Ranges

References
- Noureldin, K.; Hirsch, T.; Kuhn, P.; Nouri, B.; Yasser, Z.; Pitz-Paal, R. Modelling an Automatic Controller for Parabolic Trough Solar Fields under Realistic Weather Conditions. In Proceedings of the 23rd SolarPACES Conference, Santiago, Chile, 26–29 September 2017. [Google Scholar]
- Inman, R.H.; Pedro, H.T.C.; Coimbra, C.F.M. Solar forecasting methods for renewable energy integration. Prog. Energy Combust. Sci. 2013, 39, 535–576. [Google Scholar] [CrossRef]
- Quesada-Ruiz, S.; Chu, Y.; Tovar-Pescador, J.; Pedro, H.; Coimbra, C. Cloud tracking methodology for intra-hour DNI forecasting. Sol. Energy 2014, 102, 267–275. [Google Scholar] [CrossRef]
- Richardson, W.; Krishnaswami, H.; Vega, R.; Cervantes, M. A low cost, edge computing, all-sky imager for cloud tracking and intra-hour irradiance forecasting. Sustainability 2017, 9, 482. [Google Scholar] [CrossRef]
- Peng, Z.; Yu, D.; Huang, D.; Heiser, J.; Yoo, S.; Kalb, P. 3D cloud detection and tracking system for solar forecast using multiple sky imagers. Sol. Energy 2015, 118, 496–519. [Google Scholar] [CrossRef]
- Kazantzidis, A.; Tzoumanikas, P.; Blanc, P.; Massip, P.; Wilbert, S.; Ramirez-Santigosa, L. Short-term forecasting based on all-sky cameras. In Renewable Energy Forecasting; Kariniotakis, G., Ed.; Elsevier Science: Amsterdam, The Netherlands, 2017; pp. 153–178. [Google Scholar] [CrossRef]
- Taravat, A.; Frate, F.D.; Cornaro, C.; Vergari, S. Neural Networks and Support Vector Machine Algorithms for Automatic Cloud Classification of Whole-Sky Ground-Based Images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 666–670. [Google Scholar] [CrossRef]
- Ye, L.; Cao, Z.; Xiao, Y. DeepCloud: Ground-Based Cloud Image Categorization Using Deep Convolutional Features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5729–5740. [Google Scholar] [CrossRef]
- Heinle, A.; Macke, A.; Srivastav, A. Automatic cloud classification of whole sky images. Atmos. Meas. Tech. 2010, 3, 557–567. [Google Scholar] [CrossRef]
- Kazantzidis, A.; Tzoumanikas, P.; Bais, A.F.; Fotopoulos, S.; Economou, G. Cloud detection and classification with the use of whole-sky ground-based images. Atmos. Res. 2012, 113, 80–88. [Google Scholar] [CrossRef]
- Li, Q.; Lu, W.; Yang, J. A hybrid thresholding algorithm for cloud detection on ground-based color images. J. Atmos. Ocean Technol. 2011, 28, 1286–1296. [Google Scholar] [CrossRef]
- Huang, H.; Yoo, S.; Yu, D.; Huang, D.; Qin, H. Correlation and local feature based cloud motion estimation. In Proceedings of the Twelfth International Workshop on Multimedia Data Mining, New York, NY, USA, 12 August 2012; pp. 1–9. [Google Scholar] [CrossRef]
- Chow, C.W.; Belongie, S.; Kleissl, J. Cloud motion and stability estimation for intra-hour solar forecasting. Sol. Energy 2015, 115, 645–655. [Google Scholar] [CrossRef]
- Mejia, F.A.; Kurtz, B.; Murray, K.; Hinkelman, L.M.; Sengupta, M.; Xie, Y.; Kleissl, J. Coupling sky images with radiative transfer models: A new method to estimate cloud optical depth. Atmos. Meas. Tech. 2016, 9, 4151–4165. [Google Scholar] [CrossRef]
- Tzoumanikas, P.; Nikitidou, E.; Bais, A.F.; Kazantzidis, A. The effect of clouds on surface solar irradiance, based on data from an all-sky imaging system. Renew. Energy 2016, 95, 314–322. [Google Scholar] [CrossRef]
- Kassianov, E.; Long, C.N.; Christy, J. Cloud-base-height estimation from paired ground-based hemispherical observations. J. Appl. Meteorol. 2005, 44, 1221–1233. [Google Scholar] [CrossRef]
- Beekmans, C.; Schneider, J.; Läbe, T.; Lennefer, M.; Stachniss, C.; Simmer, C. Cloud photogrammetry with dense stereo for fisheye cameras. Atmos. Chem. Phys. 2016, 16, 14231–14248. [Google Scholar] [CrossRef]
- Fu, C.L.; Cheng, H.Y. Predicting solar irradiance with all-sky image features via regression. Sol. Energy 2013, 97, 537–550. [Google Scholar] [CrossRef]
- Bernecker, D.; Riess, C.; Angelopoulou, E.; Hornegger, J. Continuous short-term irradiance forecasts using sky images. Sol. Energy 2014, 110, 303–315. [Google Scholar] [CrossRef]
- Xia, M.; Lu, W.; Yang, J.; Ma, Y.; Yao, W.; Zheng, Z. A hybrid method based on extreme learning machine and k-nearest neighbor for cloud classification of ground-based visible cloud image. Neurocomputing 2015, 160, 238–249. [Google Scholar] [CrossRef]
- Schmidt, T.; Kalisch, J.; Lorenz, E.; Heinemann, D. Evaluating the spatio-temporal performance of sky-imager-based solar irradiance analysis and forecasts. Atmos. Chem. Phys. 2016, 16, 3399–3412. [Google Scholar] [CrossRef]
- Kuhn, P.; Nouri, B.; Wilbert, S.; Prahl, C.; Kozonek, N.; Schmidt, T.; Yasser, Z.; Ramirez, L.; Zarzalejo, L.; Meyer, A.; Vuilleumier, L.; Heinemann, D.; Blanc, P.; Pitz-Paal, R. Validation of an all-sky imager-based nowcasting system for industrial PV plants. Prog. Photovolt. Res. Appl. 2017, 26, 608–621. [Google Scholar] [CrossRef]
- Marquez, R.; Coimbra, C.F. Proposed metric for evaluation of solar forecasting models. J. Sol. Energy Eng. 2013, 135. [Google Scholar] [CrossRef]
- Nouri, B.; Wilbert, S.; Segura, L.; Kuhn, P.; Hanrieder, N.; Kazantzidis, A.; Schmidt, T.; Zarzalejo, L.; Blanc, P.; Pitz-Paal, R. Determination of cloud transmittance for all sky imager based solar nowcasting. Sol. Energy 2019, 181, 251–263. [Google Scholar] [CrossRef]
- Schroedter-Homscheidt, M.; Kosmale, M.; Jung, S.; Kleissl, J. Classifying ground-measured 1 minute temporal variability within hourly intervals for direct normal irradiances. Meteorol. Z. 2018. [Google Scholar] [CrossRef]
- Nouri, B.; Kuhn, P.; Wilbert, S.; Hanrieder, N.; Prahl, C.; Zarzalejo, L.; Kazantzidis, A.; Blanc, P.; Pitz-Paal, R. Cloud height and tracking accuracy of three all sky imager systems for individual clouds. Sol. Energy 2019, 177, 213–228. [Google Scholar] [CrossRef]
- Geuder, N.; Wolfertstetter, F.; Wilbert, S.; Schüler, D.; Affolter, R.; Kraas, B.; Lüpfert, E.; Espinar, B. Screening and flagging of solar irradiation and ancillary meteorological data. Energy Procedia 2015, 69, 1989–1998. [Google Scholar] [CrossRef]
- Wilbert, S.; Nouri, B.; Prahl, C.; Garcia, G.; Ramirez, L.; Zarzalejo, L.; Valenzuela, L.; Ferrera, F.; Kozonek, N.; Liria, J. Application of Whole Sky Imagers for Data Selection for Radiometer Calibration. In Proceedings of the EU PVSEC 2016, Munich, Germany, 20–24 June 2016; pp. 1493–1498. [Google Scholar] [CrossRef]
- Nouri, B.; Kuhn, P.; Wilbert, S.; Prahl, C.; Pitz-Paal, R.; Blanc, P.; Schmidt, T.; Yasser, Z.; Ramirez Santigosa, L.; Heineman, D. Nowcasting of DNI maps for the solar field based on voxel carving and individual 3D cloud objects from all sky images. AIP Conf. Proc. 2018. [Google Scholar] [CrossRef]
- Jung, S. Variabilität der solaren Einstrahlung in 1-Minuten aufgelösten Strahlungszeitserien. Master‘s Thesis, Universität Augsburg, Bavaria, Germany, 2015. [Google Scholar]
- Kraas, B.; Schroedter-Homscheidt, M.; Madlener, R. Economic merits of a state-of-the-art concentrating solar power forecasting system for participation in the Spanish electricity market. Sol. Energy 2013, 93, 244–255. [Google Scholar] [CrossRef]
- Perez, R.; Kivalov, S.; Schlemmer, J.; Hemker, K., Jr.; Hoff, T. Parameterization of site-specific short-term irradiance variability. Sol. Energy 2011, 85, 1343–1353. [Google Scholar] [CrossRef]
- Stein, J.S.; Hansen, C.W.; Reno, M.J. The variability index: A new and novel metric for quantifying irradiance and PV output variability. In Proceedings of the World Renewable Energy Forum, Denver, CO, USA, 13–17 May 2012. [Google Scholar]
- Coimbra, C.F.M.; Kleissl, J.; Marquez, R. Overview of Solar-Forecasting Methods and a Metric for Accuracy Evaluation. In Solar Energy Forecasting and Resource Assessment; Kleissl, J., Ed.; Academic Press: Oxford, UK, 2013; pp. 171–194. [Google Scholar]
- Hanrieder, N.; Sengupta, M.; Xie, Y.; Wilber, S.; Pitz-Paal, R. Modeling beam attenuation in solar tower plants using common DNI measurements. Sol. Energy 2016, 129, 244–255. [Google Scholar] [CrossRef]
- Wilbert, S.; Kleindiek, S.; Nouri, B.; Geuder, N.; Habte, A.; Schwandt, M.; Vignola, F. Uncertainty of rotating shadowband irradiometers and Si-pyranometers including the spectral irradiance error. AIP Conf. Proc. 2016. [Google Scholar] [CrossRef]
- Ineichen, P.; Perez, R. A new airmass independent formulation for the Linke turbidity coefficient. Sol. Energy 2002, 73, 151–157. [Google Scholar] [CrossRef]
- Schwarzbözl, P.; Gross, V.; Quaschnig, V.; Ahlbrink, N. A low-cost dynamic shadow detection system for site evaluation. In proceeding of the 17th SolarPACES, Granada, Spain, 20–23 September 2011. [Google Scholar]
- Kuhn, P.; Nouri, B.; Wilbert, S.; Hanrieder, N.; Prahl, C.; Ramirez, L.; Zarzalejo, L.; Schmidt, T.; Yasser, Z.; Heinemann, D.; Tzoumanikas, P. Determination of the optimal camera distance for cloud height measurements with two all-sky imagers. Sol. Energy 2019, 179, 74–88. [Google Scholar] [CrossRef]
- Van Den Boomgaard, R.; Van Balen, R. Methods for fast morphological image transforms using bitmapped binary images. CVGIP: Graph. Models Image Process. 1992, 54, 252–258. [Google Scholar] [CrossRef]
- Huertas-Tato, J.; Rodríguez-Benítez, F.J.; Arbizu-Barrena, C.; Aler-Mur, R.; Galvan-Leon, I.; Pozo-Vázquez, D. Automatic cloud-type classification based on the combined use of a sky camera and a ceilometer. J. Geophys. Res. Atmos. 2017, 122, 11045–11061. [Google Scholar] [CrossRef]
















| Index | Description | Unit | Introduced by |
|---|---|---|---|
| CSFD | Number of changes in the sign of the first derivative | - | [31] |
| meankcDNI | Average of clear sky index kcDNI (clear sky DNI := cDNI) | - | [32] |
| ΔkcDNI_σ | Data sample i from data package with n data samples | - | [32] |
| ΔkcDNI_mean | - | [32] | |
| ΔkcDNI_max | - | [32] | |
| ΔDNI_σ | W/m2 | [25] | |
| ΔDNI_mean | W/m2 | [25] | |
| ΔDNI_max | W/m2 | [25] | |
| VI_DNI | . | - | [33] |
| V_DNI | - | [34] | |
| Integral Upper Minus Lower (UML) | Envelope curves of DNI | J/m2 | [30] |
| Integral Upper Minus Clear (UMC) | Envelope curves of DNI | J/m2 | [30] |
| Integral Lower Minus Abscissa (LMA) | Envelope curves of DNI | J/m2 | [30] |
| Cloud Height Range | MAD Cloud Height | Cloud Speed Range | MAD Cloud Speed |
|---|---|---|---|
| 0–3000 m | 312 m | 0–6 m/s | 1.33 m/s |
| 3000–6000 m | 996 m | 6–12 m/s | 1.92 m/s |
| 6000–9000 m | 2665 m | 12–18 m/s | 2.52 m/s |
| 9000–12,000 m | 2431 m |
| Latitude | Longitude | Altitude | |
|---|---|---|---|
| PSA | 37.0909°N | 2.3581°W | 500 m |
| NETRA facility | 28.5019°N | 77.4650°E | 195 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nouri, B.; Wilbert, S.; Kuhn, P.; Hanrieder, N.; Schroedter-Homscheidt, M.; Kazantzidis, A.; Zarzalejo, L.; Blanc, P.; Kumar, S.; Goswami, N.; et al. Real-Time Uncertainty Specification of All Sky Imager Derived Irradiance Nowcasts. Remote Sens. 2019, 11, 1059. https://doi.org/10.3390/rs11091059
Nouri B, Wilbert S, Kuhn P, Hanrieder N, Schroedter-Homscheidt M, Kazantzidis A, Zarzalejo L, Blanc P, Kumar S, Goswami N, et al. Real-Time Uncertainty Specification of All Sky Imager Derived Irradiance Nowcasts. Remote Sensing. 2019; 11(9):1059. https://doi.org/10.3390/rs11091059
Chicago/Turabian StyleNouri, Bijan, Stefan Wilbert, Pascal Kuhn, Natalie Hanrieder, Marion Schroedter-Homscheidt, Andreas Kazantzidis, Luis Zarzalejo, Philippe Blanc, Sharad Kumar, Neeraj Goswami, and et al. 2019. "Real-Time Uncertainty Specification of All Sky Imager Derived Irradiance Nowcasts" Remote Sensing 11, no. 9: 1059. https://doi.org/10.3390/rs11091059
APA StyleNouri, B., Wilbert, S., Kuhn, P., Hanrieder, N., Schroedter-Homscheidt, M., Kazantzidis, A., Zarzalejo, L., Blanc, P., Kumar, S., Goswami, N., Shankar, R., Affolter, R., & Pitz-Paal, R. (2019). Real-Time Uncertainty Specification of All Sky Imager Derived Irradiance Nowcasts. Remote Sensing, 11(9), 1059. https://doi.org/10.3390/rs11091059