Combination Analysis of Future Polar-Type Gravity Mission and GRACE Follow-On
Abstract
:1. Introduction
2. Numerical Simulation Scheme
2.1. Mathematical Model for Gravity Field Recovery
2.2. Orbit Configuration Selection for FPG
2.3. Numerical Simulation Procedures
2.4. Evaluation Metrics for Recovered Gravity Field Model
3. Results and Analysis
3.1. Standalone Models of FPG
3.2. Combined Models of GFO-LRI and FPG
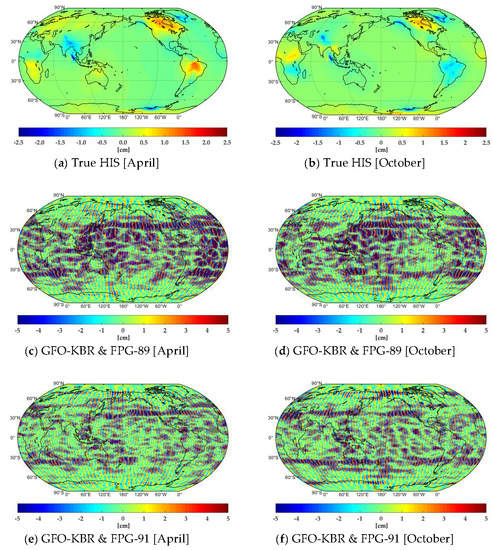
3.3. Combined Models of GFO-KBR and FPG
3.4. One-Year GFO-combined Model Series of FPG-89 and FPG-91
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kusche, J.; Klemann, V.; Sneeuw, N. Mass distribution and mass transport in the earth system: Recent scientific progress due to interdisciplinary research. Surv. Geophys. 2014, 35, 1243–1249. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Colombo, O.L. The Global Mapping of Gravity with Two Satellites; Publications on Geodesy, New Series; Netherlands Geodetic Commission: Delft, Switzerland, 1984. [Google Scholar]
- Jäggi, A.; Hugentobler, U.; Bock, H.; Beutler, G. Precise orbit determination for GRACE using undifferenced or doubly differenced GPS data. Adv. Space Res. 2007, 39, 1612–1619. [Google Scholar] [CrossRef]
- Flury, J.; Bettadpur, S.; Tapley, B.D. Precise accelerometry onboard the GRACE gravity field satellite mission. Adv. Space Res. 2008, 42, 1414–1423. [Google Scholar] [CrossRef]
- Inácio, P.; Ditmar, P.; Klees, R.; Farahani, H.H. Analysis of star camera errors in GRACE data and their impact on monthly gravity field models. J. Geod. 2015, 89, 551–571. [Google Scholar] [CrossRef] [Green Version]
- Dahle, C.; Murböck, M.; Flechtner, F.; GFZ GRACE/GRACE-FO SDS Team. Level-2 GRACE RL06 Products from GFZ. Presented at the GRACE/GRACE-FO Science Team Meeting, Potsdam, Germany, 9 October 2018; Available online: https://presentations.copernicus.org/GSTM-2018-90_presentation.pdf (accessed on 19 January 2019).
- Meyer, U.; Jäggi, A.; Jean, Y.; Beutler, G. AIUB-RL02: An improved time-series of monthly gravity fields from GRACE data. Geophys. J. Int. 2016, 205, 1196–1207. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, Q.; Xu, H. Monthly gravity field solution from GRACE range measurements using modified short arc approach. Geod. Geodyn. 2015, 6, 261–266. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Shen, Y.; Chen, W.; Zhang, X.; Hsu, H. An improved GRACE monthly gravity field solution by modelling the non-conservative acceleration and attitude observation errors. J. Geod. 2016, 90, 503–523. [Google Scholar] [CrossRef]
- Chen, Q.; Shen, Y.; Francis, O.; Chen, W.; Zhang, X.; Hsu, H. Tongji-Grace02s and Tongji-Grace02k: High-Precision Static GRACE-Only Global Earth’s Gravity Field Models Derived by Refined Data Processing Strategies. J. Geophys. Res. Solid Earth 2018, 123, 6111–6137. [Google Scholar] [CrossRef]
- Chen, J.L.; Tapley, B.D.; Save, H.; Tamisiea, M.E.; Bettadpur, S.; Ries, J. Quantification of ocean mass change using GRACE gravity, satellite altimeter and Argo floats observations. J. Geophys. Res. Solid Earth 2018. [Google Scholar] [CrossRef]
- WCRP Global Sea Level Budget Group. Global sea-level budget 1993–present. Earth Syst. Sci. Data 2018, 10, 1551–1590. [Google Scholar] [CrossRef]
- Feng, W.; Zhong, M.; Lemoine, J.M.; Biancale, R.; Hsu, H.T.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef] [Green Version]
- Feng, W.; Shum, C.K.; Zhong, M.; Pan, Y. Groundwater Storage Changes in China from Satellite Gravity: An Overview. Remote Sens. 2018, 10, 674. [Google Scholar] [CrossRef]
- Chen, T.; Shen, Y.; Chen, Q. Mass flux solution in the Tibetan Plateau using mascon modeling. Remote Sens. 2016, 8, 439. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Blankenship, D.; Young, D. Antarctic regional ice loss rates from GRACE. Earth Planet. Sci. Lett. 2008, 266, 140–148. [Google Scholar] [CrossRef]
- Flechtner, F.; Neumayer, K.H.; Dahle, C.; Dobslaw, H.; Fagiolini, E.; Raimondo, J.C.; Guntner, A. What Can be Expected from the GRACE-FO Laser Ranging Interferometer for Earth Science Applications? Surv. Geophys. 2016, 37, 453–470. [Google Scholar] [CrossRef]
- Frank, W. GRACE-FO Mission Status and Further Plans. Presented at the GRACE/GRACE-FO Science Team Meeting, Potsdam, Germany, 9 October 2018. [Google Scholar]
- Sheard, B.S.; Heinzel, G.; Danzmann, K.; Shaddock, D.A.; Klipstein, W.M.; Folkner, W.M. Intersatellite laser ranging instrument for the GRACE follow-on mission. J. Geod. 2012, 86, 1083–1095. [Google Scholar] [CrossRef]
- Loomis, B.D.; Nerem, R.S.; Luthcke, S.B. Simulation study of a follow-on gravity mission to GRACE. J. Geod. 2012, 86, 319–335. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Willsky, A.S.; Nawab, S.H. Signals and Systems, 2nd ed.; Prentice Hall: Upper Saddle River, New Jersey, USA, 1996. [Google Scholar]
- Han, S.C.; Jekeli, C.; Shum, C.K. Time-variable aliasing effects of ocean tides, atmosphere, and continental water mass on monthly mean GRACE gravity field. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Dobslaw, H.; Bergmann-Wolf, I.; Dill, R.; Forootan, E.; Klemann, V.; Kusche, J.; Sasgen, I. The updated ESA Earth System Model for future gravity mission simulation studies. J. Geod. 2015, 89, 505–513. [Google Scholar] [CrossRef]
- Dobslaw, H.; Bergmann-Wolf, I.; Dill, R.; Poropat, L.; Thomas, M.; Dahle, C.; Esselborn, S.; Konig, R.; Flechtner, F. A new high-resolution model of non-tidal atmosphere and ocean mass variability for de-aliasing of satellite gravity observations: AOD1B RL06. Geophys. J. Int. 2017, 211, 263–269. [Google Scholar] [CrossRef] [Green Version]
- Seo, K.W.; Wilson, C.R.; Han, S.C.; Waliser, D.E. Gravity Recovery and Climate Experiment (GRACE) alias error from ocean tides. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Dobslaw, H.; Bergmann-Wolf, I.; Forootan, E.; Dahle, C.; Mayer-Gürr, T.; Kusche, J.; Flechtner, F. Modeling of present-day atmosphere and ocean non-tidal de-aliasing errors for future gravity mission simulations. J. Geod. 2016, 90, 423–436. [Google Scholar] [CrossRef] [Green Version]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Kusche, J.; Schmidt, R.; Petrovic, S.; Rietbroek, R. Decorrelated GRACE time-variable gravity solutions by GFZ, and their validation using a hydrological model. J. Geod. 2009, 83, 903–913. [Google Scholar] [CrossRef] [Green Version]
- Visser, P.N.A.M.; Sneeuw, N.; Reubelt, T.; Losch, M.; van Dam, T. Space-borne gravimetric satellite constellations and ocean tides: Aliasing effects. Geophys. J. Int. 2010, 181, 789–805. [Google Scholar] [CrossRef]
- Wiese, D.N.; Visser, P.; Nerem, R.S. Estimating low resolution gravity fields at short time intervals to reduce temporal aliasing errors. Adv. Space Res. 2011, 48, 1094–1107. [Google Scholar] [CrossRef]
- Daras, I.; Pail, R. Treatment of temporal aliasing effects in the context of next generation satellite gravimetry missions. J. Geophys. Res. Solid Earth 2017, 122, 7343–7362. [Google Scholar] [CrossRef]
- Hauk, M.; Pail, R. Treatment of ocean tide aliasing in the context of a next generation gravity field mission. Geophys. J. Int. 2018, 214, 345–365. [Google Scholar] [CrossRef]
- Wiese, D.N.; Folkner, W.M.; Nerem, R.S. Alternative mission architectures for a gravity recovery satellite mission. J. Geod. 2009, 83, 569–581. [Google Scholar] [CrossRef]
- Bender, P.; Wiese, D.; Nerem, R. A possible dual-GRACE mission with 90 degree and 63 degree inclination orbits. In Proceedings of the International Symposium on Formation Flying, Noordwijk, The Netherlands, 23–25 April 2008; Eur. Space Agency: Noordwijk, The Netherlands, 2008. [Google Scholar]
- Wiese, D.N.; Nerem, R.S.; Lemoine, F.G. Design considerations for a dedicated gravity recovery satellite mission consisting of two pairs of satellites. J. Geod. 2012, 86, 81–98. [Google Scholar] [CrossRef]
- Sneeuw, N.; Sharifi, M.; Keller, W. Gravity Recovery from Formation Flight Missions. In VI Hotine-Marussi Symposium on Theoretical and Computational Geodesy; Xu, P., Liu, J., Dermanis, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 132, pp. 29–34. [Google Scholar]
- Elsaka, B.; Raimondo, J.C.; Brieden, P.; Reubelt, T.; Kusche, J.; Flechtner, F.; Pour, S.I.; Sneeuw, N.; Muller, J. Comparing seven candidate mission configurations for temporal gravity field retrieval through full-scale numerical simulation. J. Geod. 2014, 88, 31–43. [Google Scholar] [CrossRef]
- Cesare, S.; Sechi, G. Next Generation Gravity Mission. In Distributed Space Missions for Earth System Monitoring; D’Errico, M., Ed.; Springer: New York, NY, USA, 2013; Volume 31, pp. 575–598. [Google Scholar]
- Pail, R.; Gruber, T.; Abrykosov, P.; Hauk, M.; Purkhauser, A. Assessment of NGGM Concepts for Sustained Observation of Mass Transport in the Earth System. Presented at the GRACE/GRACE-FO Science Team Meeting, Potsdam, Germany, 10 October 2018; Available online: https://meetingorganizer.copernicus.org/GSTM-2018/GSTM-2018-10.pdf (accessed on 19 January 2019).
- Hsu, H.; Zhong, M.; Feng, W.; Wang, C. Overwiew of activities of Chinese gravity mission. Presented at the International Symposium on Geodesy and Geodynamics (ISGG2018)-Tectonics, Earthquake and Geohazards, Kunming, China, 31 July 2018. [Google Scholar]
- Reigber, C. Gravity field recovery from satellite tracking data. In Theory of Satellite Geodesy and Gravity Field Determination; Sansò, F., Rummel, R., Eds.; Springer: Berlin/Heidelberg, Germany, 1989; Volume 25, pp. 197–234. [Google Scholar]
- Zhou, H.; Luo, Z.; Zhou, Z.; Li, Q.; Zhong, B.; Lu, B.; Hsu, H. Impact of Different Kinematic Empirical Parameters Processing Strategies on Temporal Gravity Field Model Determination. J. Geophys. Res. Solid Earth 2018. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, Q.; Ditmar, P.; Sun, Y.; Liu, J. Improvements in the Monthly Gravity Field Solutions Through Modeling the Colored Noise in the GRACE Data. J. Geophys. Res. Solid Earth 2018, 123, 7040–7054. [Google Scholar] [CrossRef]
- Wang, C.; Xu, H.; Zhong, M.; Feng, W. Monthly gravity field recovery from GRACE orbits and K-band measurements using variational equations approach. Geod. Geodyn. 2015, 6, 253–260. [Google Scholar] [CrossRef] [Green Version]
- Kaula, W.M. Theory of Satellite Geodesy: Applications of Satellites to Geodesy; Dover Publications: New York, NY, USA, 2000. [Google Scholar]
- Chen, Q.; Shen, Y.; Zhang, X.; Hsu, H.; Chen, W.; Ju, X.; Lou, L. Monthly gravity field models derived from GRACE Level 1B data using a modified short-arc approach. J. Geophys. Res. Solid Earth 2015, 120, 1804–1819. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y. Algorithm Characteristics of Dynamic Approach-based Satellite Gravimetry and Its Improvement Proposals. Acta Geod. Cartogr. Sin. 2017, 46, 1308–1315. (In Chinese) [Google Scholar]
- Montenbruck, O.; Gill, E. Satellite Orbits-Models, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Kim, J. Simulation Study of a Low-Low Satellite-to-Satellite Tracking Mission. Ph.D. Thesis, The University of Texas, Austin, TX, USA, 2000. [Google Scholar]
- Daras, I. Gravity Field Processing towards Future LL-SST Satellite Missions. Ph.D. Thesis, Technische Universität München, München, Germany, 2016. [Google Scholar]
- Vallado, D. Fundamentals of Astrodynamics and Applications, 4th ed.; Microcosm Press: El Segundo, CA, USA, 2013. [Google Scholar]
- Reigber, C.; Lühr, H.; Schwintzer, P. CHAMP mission status. Adv. Space Res. 2002, 30, 129–134. [Google Scholar] [CrossRef]
- Rummel, R.; Yi, W.; Stummer, C. GOCE gravitational gradiometry. J. Geod. 2011, 85, 777–790. [Google Scholar] [CrossRef]
- Förste, C.; Bruinsma, S.L.; Abrikosov, O.; Lemoine, J.; Marty, J.C.; Flechtner, F.; Balmino, G.; Barthelmes, F.; Biancale, R. EIGEN-6C4 The Latest Combined Global Gravity Field Model Including GOCE Data up to Degree and Order 2190 of GFZ Potsdam and GRGS Toulouse. GFZ Data Services. 2014. Available online: http://icgem.gfz-potsdam.de/getmodel/zip/7fd8fe44aa1518cd79ca84300aef4b41ddb2364aef9e82b7cdaabdb60a9053f1 (accessed on 19 January 2019).
- Savcenko, R.; Bosch, W. EOT11a-Empirical Ocean Tide Model from Multi-Mission Satellite Altimetry; Deutsches Geodätisches Forschungsinstitut (DGFI): München, Germany, 2012. [Google Scholar]
- Darbeheshti, N.; Wegener, H.; Müller, V.; Naeimi, M.; Heinzel, G.; Hewitson, M. Instrument data simulations for GRACE Follow-on: Observation and noise models. Earth Syst. Sci. Data 2017, 9, 833–848. [Google Scholar] [CrossRef]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Wiese, D.N. Optimizing Two Pairs of GRACE-like Satellites for Recovering Temporal Gravity Variations. Ph.D. Theses, University of Colorado, Boulder, CO, USA, 2011. [Google Scholar]
- Meyer, U.; Jean, Y.; Arnold, D.; Jäggi, A.; Kvas, A.; Mayer-Gürr, T.; Lemoine, J.M.; Bourgogne, S.; Dahle, C.; Flechtner, F. The EGSIEM combination service: Final results and further plans. In Proceedings of the EGU General Assembly 2018, Vienna, Austria, 8–13 April 2018; Available online: https://boris.unibe.ch/116268/1/EGU18_EGSIEM-1.pdf (accessed on 19 January 2019).
- Feng, W. GRAMAT: A comprehensive Matlab toolbox for estimating global mass variations from GRACE satellite data. Earth Sci. Inform. 2018, 1–16. [Google Scholar] [CrossRef]









| Orbit Configuration | Altitude (km) | Inclination (deg.) | Eccentricity | Inter-Satellite Distance (km) |
|---|---|---|---|---|
| GFO | 490 | 89 | 0.0015 | 220 |
| FPG-87 | 500 | 87 | 0.0015 | 220 |
| FPG-89 | 89 | |||
| FPG-91 | 91 | |||
| FPG-93 | 93 |
| Force Categories | True Model | Reference Model |
|---|---|---|
| Static Field | EIGEN6C4 (100 d/o) | EIGEN6C4 (100 d/o) |
| Ocean Tide | EOT11a (100 d/o) | FES2004 (100 d/o) |
| Non-tidal Variation | ESM AOHIS (100 d/o) | ESM DEAL + AOerr (100 d/o) |
| Obs. Type | Orbit Pos. | GFO/FPG-KBR | GFO-LRI | Accelerometer |
|---|---|---|---|---|
| SD Value | 1 cm | 0.2 μm/s | 10 nm/s | 0.3 nm/s2 |
| Degree | GFO-KBR & FPG-87 | GFO-KBR & FPG-89 | GFO-KBR & FPG-91 | GFO-KBR & FPG-93 |
|---|---|---|---|---|
| 25 | −3.6% | 16.7% | 7.9% | 7.9% |
| 50 | 17.5% | 15.1% | 14.6% | 16.7% |
| 75 | 31.1% | 16.7% | 33.6% | 41.6% |
| 100 | 28.0% | 14.7% | 39.5% | 31.7% |
| Area | wRMS of GFO & FPG-89 (cm) | wRMS of GFO & FPG-91 (cm) | GFO & FPG-91 Error Reduction Rate (%) |
|---|---|---|---|
| Amazon | 2.76 | 1.98 | 28.3 |
| North Murray–Darling | 3.56 | 2.54 | 28.7 |
| Yangtze | 2.63 | 2.32 | 11.8 |
| NCP | 3.19 | 2.89 | 9.4 |
| Greenland | 1.01 | 1.15 | -13.9 |
| Ocean | 3.09 | 2.41 | 22.0 |
| Land | 2.53 | 2.09 | 17.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, Y.; Shen, Y.; Chen, Q. Combination Analysis of Future Polar-Type Gravity Mission and GRACE Follow-On. Remote Sens. 2019, 11, 200. https://doi.org/10.3390/rs11020200
Nie Y, Shen Y, Chen Q. Combination Analysis of Future Polar-Type Gravity Mission and GRACE Follow-On. Remote Sensing. 2019; 11(2):200. https://doi.org/10.3390/rs11020200
Chicago/Turabian StyleNie, Yufeng, Yunzhong Shen, and Qiujie Chen. 2019. "Combination Analysis of Future Polar-Type Gravity Mission and GRACE Follow-On" Remote Sensing 11, no. 2: 200. https://doi.org/10.3390/rs11020200
APA StyleNie, Y., Shen, Y., & Chen, Q. (2019). Combination Analysis of Future Polar-Type Gravity Mission and GRACE Follow-On. Remote Sensing, 11(2), 200. https://doi.org/10.3390/rs11020200