Machine Learning Regression Approaches for Colored Dissolved Organic Matter (CDOM) Retrieval with S2-MSI and S3-OLCI Simulated Data
Abstract
:1. Introduction
2. Datasets and Methods
2.1. Datasets
2.2. Established Approaches Using Band Ratio Algorithms
2.3. Machine Learning Approaches
2.3.1. Multivariate Linear Regression
2.3.2. Decision Trees and Random Forests
2.3.3. Kernel Methods
Kernel ridge regression
Gaussian process regression
Support vector regression
2.4. Comparison, Implementation and Reproducibility
3. Experimental Results
3.1. Experiments Setup
3.2. Analysis of the Models
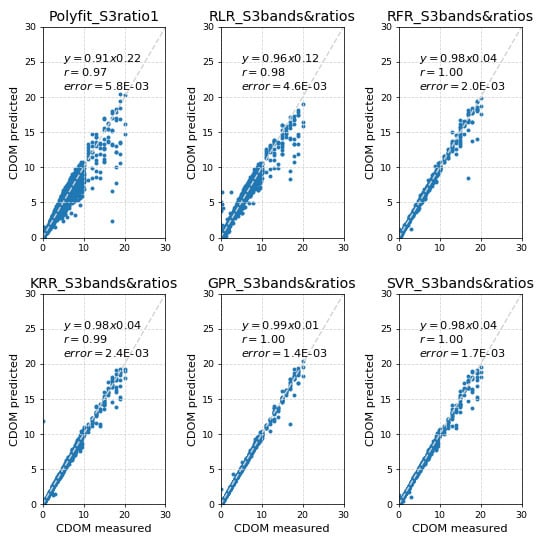
3.2.1. Sentinel 2 MSI Data
3.2.2. Sentinel 3 OLCI Data
3.2.3. Application of the Models to the C2X Dataset
3.2.4. Predicted vs. Measured CDOM with the C2X Dataset
4. Comparison of the C2X Experiment with Neural Nets
4.1. Comparison of the Results Extracted with OLCI Neural Net Swarm
4.2. Comparison Against the Standard S3-OLCI Product
- The Baseline Atmospheric Correction (BPAC) removes all the contributions to TOA reflectance, including glint correction and white cap effects. Later in the processing it estimates the near-infra-red water-leaving reflectance to perform the atmospheric correction.
- The Alternate Atmospheric Correction (AAC) uses a neural network approach to provide water-leaving reflectance, but these products are not written by default in the standard L2 provided by EUMETSAT.
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Preisendorfer, R.W. Hydrologic Optics; U.S. Department of Commerce; National Oceanic and Atmospheric Administration; Environmental Research Laboratories; Pacific Marine Environmental Laboratory: Honolulu, HI, USA, 1976.
- Jerlov, N. Marine Optics, 2nd ed.; Elsevier Science: New York, NY, USA, 1976; Volume14, p. 230. [Google Scholar]
- Mobley, C. Light and Water: Radiative Transfer in Natural Waters; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Mobley, C.; Sundman, L.K. HydroLight 5.2, Ecolight 5.2, Technical Documentation; Technical Report; Sequoia Science Inc.: Bellevue, WA, USA, 2013. [Google Scholar]
- Morel, M.; Prieur, L. Analysis of variations in ocean color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Dekker, A. Detection of Optical Water Quality Parameters for Eutrophic Waters by High Resolution Remote Sensing. Ph.D. Thesis, Vrije Universiteit, Amsterdam, The Netherlands, 1993. [Google Scholar]
- Bukata, R.; Jerome, J.; Kondratyev, K.; Pozdnaykov, D. Optical Properties and Remote Sensing of Inland and Coastal Waters; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Simis, S.; Tijdens, M.; Peters, S.; Gons, H. Optical characterization of cyanobacterial bloom termination. Verhandlungen Internationale Vereinigung fur Theoretische und Angewandte Limnologie 2005, 29, 941–944. [Google Scholar] [CrossRef]
- Moses, W.; Gitelson, A.; Berdnikov, S.; Povazhnyy, V. Estimation of chlorophyll- a concentration in case II waters using MODIS and MERIS data: successes and challenges. Environ. Res. Lett. 2009, 4, 045005. [Google Scholar] [CrossRef]
- Giardino, C.; Bartoli, M.; Candianai, G.; Brescian, M.; Pellegrini, L. Recent changes in macrophyte colonisation patterns: an imaging spectrometry-based evaluation of southern Lake Garda (Northern Italy). J. Appl. Remote Sens. 2007, 1, 011509. [Google Scholar]
- Kallio, K. Optical properties of Finnish lakes estimated with simple bio-optical models and water quality monitoring data. Hydrol. Res. 2006, 37, 183–204. [Google Scholar] [CrossRef]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef] [Green Version]
- Guanter, L.; Ruiz-Verdu, A.; Odermatt, D.; Giardino, C.; Simis, S.; Estelles, V.; Heege, T.; Dominguez-Gomez, J.A.; Moreno, J. Atmospheric correction of ENVISAT/MERIS data over inland waters: Validation for European lakes. Remote Sens. Environ. 2010, 114, 467–480. [Google Scholar] [CrossRef] [Green Version]
- Hieronymi, M.; Krasemann, H.; Mueller, D.; Brockmann, C.; Ruescas, A.; Stelzer, K.; Nechad, B.; Ruddick, K.; Simis, S.; Tisltone, G.; Steinmetz, F.; Regner, P. Ocean Colour Remote Sensing of Extreme Case-2 Waters. In Proceedings of the 2016 ESA Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- Toming, K.; Kutser, T.; Uiboupin, R.; Arikas, A.; Vahter, K.; Paavel, B. Mapping Water Quality Parameters with Sentinel-3 Ocean and Land Colour Instrument imagery in the Baltic Sea. Remote Sens. 2017, 9, 1070. [Google Scholar] [CrossRef]
- Tehrani, N.; DSa, E.; Osburn, C.; Bianchi, T.; Schaeffer, B. Chromophoric Dissolved Organic Matter and Dissolved Organic Carbon from Sea-Viewing Wide Field-of-View Sensor (SeaWiFS), Moderate Resolution Imaging Spectroradiometer (MODIS) and MERIS Sensors: Case Study for the Northern Gulf of Mexico. Remote Sens. 2013, 5, 1439–1464. [Google Scholar] [CrossRef]
- Kutser, T.; Paavel, B.; Verpoorter, C.; Ligi, M.; Soomets, T.; Toming, K.; Casal, G. Remote Sensing of Black Lakes and Using 810 nm Reflectance Peak for Retrieving Water Quality Parameters of Optically Complex Waters. Remote Sens. 2016, 8, 497. [Google Scholar] [CrossRef]
- Kallio, K. Water Quality Estimation by Optical Remote Sensing in Boreal Lakes; Monographs of the Boreal Environment Research 39; The Finnish Environment Institute: Helsinki, Finland, 2012. [Google Scholar]
- Kallio, K.; Koponen, S.; Ylöstalo, P.; Kervinen, M.; Pyhälahti, T.; Attila, J. Validation of MERIS spectral inversion processors using reflectance, IOP and water quality measurements in boreal lakes. Remote Sens. Environ. 2015, 157, 147–157. [Google Scholar] [CrossRef]
- Kortelainen, P. Content of Total Organic Carbon in Finnish Lakes and Its Relationship to Catchment Characteristics. Can. J. Fish. Aquat. Sci. 1993, 50, 1477–1483. [Google Scholar] [CrossRef]
- Attila, J.; Koponen, S.; Kallio, K.; Lindfors, A.; Kaitala, S.; Ylöstalo, P. MERIS Case II water processor comparison on coastal sites of the northern Baltic Sea. Remote Sens. Environ. 2013, 128, 138–149. [Google Scholar] [CrossRef]
- Beltran-Abaunza, J.M.; Kratzer, S.; Brockmann, C. Evaluation of MERIS products from Baltic Sea coastal waters rich in CDOM. Ocean Sci. 2014, 10, 377–396. [Google Scholar] [CrossRef]
- Brezonik, P.; Olmanson, L.; Finlay, J.; Bauer, M. Factors affecting the measurement of CDOM by remote sensing of optically complex inland waters. Remote Sens. Environ. 2015, 157, 199–215. [Google Scholar] [CrossRef]
- Alikas, K.; Lautt, S.; Reinart, A. D3.4 Adapated Water Quality Algorithms; Technical Report, GLaSS Project, H2020; European Union: Brussels, Belgium, 2014. [Google Scholar]
- Doerffer, R.; Schiller, H. The MERIS Case 2 water algorithm. Int. J. Remote Sens. 2007, 28, 517–535. [Google Scholar] [CrossRef]
- Doerffer, R. OLCI L2 ATBD; Technical Report; GKSS: Gothenburg, Sweden, 2011. [Google Scholar]
- Brockmann, C.; Doerffer, R.; Peters, M.; Stelzer, K.; Embacher, S.; Ruescas, A. Evolution of the C2RCC neural network for Sentinel 2 and 3 for the retrieval of ocean colour products in normal and extreme optically complex waters. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- Hieronymi, M.; Mueller, D.; Doerffer, R. The OLCI Neural Network Swarm (ONNS): A Bio-Geo-Optical Algorithm for Open Ocean and Coastal Waters. Front. Mar. Sci. 2017, 4, 140. [Google Scholar] [CrossRef]
- Ylöstalo, P.; Kallio, K.; Seppälä, J. Absorption properties of in-water constituents and their variation among various lake types in the boreal region. Remote Sens. Environ. 2014, 148, 190–205. [Google Scholar] [CrossRef]
- Hieronymi, M.; Kraseman, H.; Ruescas, A.; Brockmann, C.; Steinmetz, F.; Tilstone, G.; Simis, S. Algorithm Theoretical Basis Document; Technical Report, Case 2 eXtreme Project; ESA: Paris, France, 2015. [Google Scholar]
- Kraseman, H.; Hieronymi, M.; Simis, S.; Steinmetz, F.; Tilstone, G.; Nechad, B.; Kraemer, U. Database for Task 2, Technical Note; Technical Report, Case 2 eXtreme Project; ESA: Paris, France, 2016. [Google Scholar]
- Breiman, L.; Friedman, J. Estimating Optimal Transformations for Multiple Regression and Correlation. J. Am. Statist. Assoc. 1985, 80, 1580–1598. [Google Scholar]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; The MIT Press: New York, NY, USA, 2006. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Evans, J.S.; Cushman, S.A. Gradient modeling of conifer species using random forests. Landsc. Ecol. 2009, 24, 673–683. [Google Scholar] [CrossRef]
- Oliveira, S.; Oehler, F.; San-Miguel-Ayanz, J.; Camia, A.; Pereira, J.M. Modeling spatial patterns of fire occurrence in Mediterranean Europe using Multiple Regression and Random Forest. For. Ecol. Manage. 2012, 275, 117–129. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random Forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forest for classification in Ecolog. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Jung, M.; Zscheischler, J. A Guided Hybrid Genetic Algorithm for Feature Selection with Expensive Cost Functions. Procedia Comput. Sci. 2013, 18, 2337–2346. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Bruzzone, L. Kernel methods for Remote Sensing Data Analysis; Wiley & Sons: Oxford, UK, 2009. [Google Scholar]
- Camps-Valls, G.; Verrelst, J.; Munoz-Mari, J.; Laparra, V.; Mateo-Jimenez, F.; Gomez-Dans, J. A Survey on Gaussian Processes for Earth Observation Data Analysis. IEEE Geosci. Remote Sens. Mag. 2016, 4, 58–78. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Gestel, T.V.; Brabanter, J.D.; Moor, B.D.; Vandewalle, J. (Eds.) Least Squares Support Vector Machines; World Scientific Publishing Co.: Singapore, 2002. [Google Scholar]
- Furfaro, R.; Morris, R.D.; Kottas, A.; Taddy, M.; Ganapol, B.D. A Gaussian Process Approach to Quantifying the Uncertainty of Vegetation Parameters from Remote Sensing Observations. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 11–15 December 2006. [Google Scholar]
- Verrelst, J.; Muñoz, J.; Alonso, L.; Delegido, J.; Rivera, J.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Verrelst, J.; Alonso, L.; Camps-Valls, G.; Delegido, J.; Moreno, J. Retrieval of vegetation biophysical parameters using Gaussian process techniques. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1832–1843. [Google Scholar] [CrossRef]
- Blix, K.; Jenssen, R.; Camps-Valls, G. Gaussian Process Sensitivity Analysis for Oceanic Chlorophyll Estimation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 1, 1–13. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A. Learning with Kernels—Support Vector Machines, Regularization, Optimization and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Anderson, M.; Robinson, J. Permutation Tests for Linear Models. Aust. N. Z. J. Stat. 2001, 43, 75–88. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Jung, M.; Ichii, K.; Papale, D.; Tramontana, G.; Bodesheim, P.; Schwalm, C.; Zscheischler, J.; Mahecha, M.; Reichstein, M. Ranking drivers of global carbon and energy fluxes over land. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar]














| Sensor | Spatial Resolution (m) | Band Number | Central Wavelength (nm) | Bandwidth (nm) |
|---|---|---|---|---|
| S2-MSI | 10 | 2 | 496.6 | 98 |
| 3 | 560.0 | 45 | ||
| 4 | 664.5 | 38 | ||
| 8 | 835.1 | 145 | ||
| 20 | 5 | 703.9 | 19 | |
| 6 | 740.2 | 18 | ||
| 7 | 782.5 | 28 | ||
| 8a | 864.8 | 33 | ||
| 11 | 1613.7 | 143 | ||
| 12 | 2202.4 | 242 | ||
| 60 | 1 | 443.9 | 27 | |
| 9 | 945.0 | 26 | ||
| 10 | 1373.5 | 75 | ||
| S3-OLCI | 300 | Oa1 | 400.0 | 15 |
| Oa2 | 412.5 | 10 | ||
| Oa3 | 442.5 | 10 | ||
| Oa4 | 490.0 | 10 | ||
| Oa5 | 510.0 | 10 | ||
| Oa6 | 560.0 | 10 | ||
| Oa7 | 620.0 | 10 | ||
| Oa8 | 665.0 | 10 | ||
| Oa9 | 673.75 | 7.5 | ||
| Oa10 | 681.25 | 7.5 | ||
| Oa11 | 708.75 | 10 | ||
| Oa12 | 753.75 | 7.5 | ||
| Oa13 | 761.25 | 2.5 | ||
| Oa14 | 764.375 | 3.75 | ||
| Oa15 | 767.5 | 2.5 | ||
| Oa16 | 778.75 | 15 | ||
| Oa17 | 865.0 | 20 | ||
| Oa18 | 885.0 | 10 | ||
| Oa19 | 900.0 | 10 | ||
| Oa20 | 940.0 | 20 | ||
| Oa21 | 1020 | 40 |
| Method | Train Cost | Test Cost | Train Memory | Test Memory | Pros | Cons |
|---|---|---|---|---|---|---|
| RLR | Simple, fast | Cannot cope with nonlinear relations | ||||
| RFR | Fast, parallelizable | Do not provide confidence intervals, heuristic parameters to tune, prone to outliers | ||||
| KRR | Fast for moderate sample sizes (), effective | Do not provide confidence intervals, prone to outliers | ||||
| GPR | Accurate, confidence intervals for predictions, automatic estimation of spectral bands and noise variance | Slow in moderate sample sizes | ||||
| SVR | Generally accurate and robust to outliers | Slow, three hyper-parameters to tune by cross-validation |
| R2 | Bias | MAE | R | RMSE | RMSErel | |
|---|---|---|---|---|---|---|
| S2-Ratio 1: | ||||||
| Polyfit | 0.934 | 0.004 | 1.068 | 0.966 | 2.054 | 0.133 |
| RLR | 0.887 | 0.657 | 1.747 | 0.942 | 2.684 | 0.768 |
| RFR | 0.895 | −0.043 | 1.334 | 0.946 | 2.578 | 0.170 |
| KRR | 0.933 | 0.005 | 1.052 | 0.966 | 2.059 | 0.134 |
| GPR | 0.934 | 0.014 | 1.057 | 0.966 | 2.057 | 0.133 |
| SVR | 0.928 | −0.281 | 1.026 | 0.966 | 2.136 | 0.130 |
| S2-Ratio 2: | ||||||
| Polyfit | 0.966 | −0.001 | 0.917 | 0.983 | 1.472 | 0.168 |
| RLR | 0.949 | 0.026 | 1.143 | 0.974 | 1.806 | 0.385 |
| RFR | 0.949 | −0.035 | 1.138 | 0.974 | 1.811 | 0.189 |
| KRR | 0.967 | −0.005 | 0.916 | 0.983 | 1.454 | 0.168 |
| GPR | 0.967 | −0.004 | 0.916 | 0.983 | 1.456 | 0.168 |
| SVR | 0.964 | 0.224 | 0.893 | 0.982 | 1.550 | 0.177 |
| S2 two ratios: | ||||||
| RLR | 0.949 | 0.026 | 1.145 | 0.974 | 1.806 | 0.388 |
| RFR | 0.969 | −0.018 | 0.784 | 0.984 | 1.410 | 0.121 |
| KRR | 0.974 | 0.010 | 0.75 | 0.987 | 1.293 | 0.117 |
| GPR | 0.976 | −0.005 | 0.748 | 0.986 | 1.346 | 0.115 |
| SVR | 0.974 | 0.065 | 0.745 | 0.987 | 1.283 | 0.118 |
| S2 all bands, | ||||||
| RLR | 0.484 | 0.124 | 3.957 | 0.696 | 5.735 | 1.626 |
| RFR | 0.978 | −0.049 | 0.295 | 0.990 | 1.164 | 0.074 |
| KRR | 0.997 | 0.006 | 0.210 | 0.999 | 0.408 | 0.06 |
| GPR | 0.998 | −0.003 | 0.027 | 0.999 | 0.359 | 0.033 |
| SVR | 0.993 | −0.002 | 0.092 | 0.996 | 0.670 | 0.068 |
| S2 all bands + ratios, | ||||||
| RLR | 0.987 | 0.015 | 0.619 | 0.993 | 0.917 | 0.243 |
| RFR | 0.997 | −0.009 | 0.145 | 0.998 | 0.447 | 0.038 |
| KRR | 0.998 | −0.005 | 0.039 | 0.999 | 0.475 | 0.064 |
| GPR | 0.995 | 0.022 | 0.029 | 0.997 | 0.190 | 0.022 |
| SVR | 0.999 | −0.012 | 0.044 | 0.999 | 0.182 | 0.022 |
| SYKE | C2X | |||||||
|---|---|---|---|---|---|---|---|---|
| R2 | Bias | MAE | RMSEr | R2 | Bias | MAE | RMSEr | |
| S3-Ratio 1 | ||||||||
| Polyfit | 0.936 | 0.004 | 1.048 | 0.133 | 0.931 | −0.083 | 0.555 | 0.944 |
| RLR | 0.891 | 0.064 | 1.710 | 0.746 | 0.919 | −0.059 | 0.695 | 1.547 |
| RFR | 0.899 | 0.029 | 1.330 | 0.174 | 0.901 | −0.038 | 0.640 | 1.298 |
| KRR | 0.936 | 0.005 | 1.033 | 0.133 | 0.935 | −0.067 | 0.523 | 0.587 |
| GPR | 0.932 | 0.013 | 1.037 | 0.132 | 0.935 | −0.064 | 0.523 | 0.630 |
| SVR | 0.936 | −0.254 | 1.010 | 0.129 | 0.926 | −0.219 | 0.532 | 0.631 |
| S3-Ratio 2 | ||||||||
| Polyfit | 0.959 | −0.006 | 0.995 | 0.186 | 0.868 | −0.115 | 0.712 | 5.110 |
| RLR | 0.948 | 0.015 | 1.139 | 0.325 | 0.646 | −0.133 | 1.376 | 8.473 |
| RFR | 0.933 | −0.048 | 1.228 | 0.206 | 0.861 | −0.102 | 0.693 | 3.844 |
| KRR | 0.960 | −0.010 | 0.996 | 0.185 | 0.898 | −0.131 | 0.585 | 3.510 |
| GPR | 0.960 | −0.009 | 0.996 | 0.196 | 0.893 | −0.141 | 0.578 | 3.696 |
| SVR | 0.958 | 0.264 | 0.967 | 0.186 | 0.847 | −0.238 | 0.689 | 4.021 |
| S3 two ratios | ||||||||
| RLR | 0.949 | 0.024 | 1.130 | 0.407 | 0.924 | −0.076 | 0.689 | 2.306 |
| RFR | 0.968 | −0.033 | 0.797 | 0.119 | 0.959 | −0.080 | 0.392 | 0.529 |
| KRR | 0.973 | 0.007 | 0.750 | 0.117 | 0.957 | −0.101 | 0.429 | 0.435 |
| GPR | 0.968 | −0.014 | 0.760 | 0.114 | 0.953 | −0.081 | 0.397 | 1.073 |
| SVR | 0.974 | 0.072 | 0.748 | 0.119 | 0.956 | −0.180 | 0.393 | 0.477 |
| S3 all bands | ||||||||
| RLR | 0.580 | 0.036 | 3.100 | 1.483 | 0.605 | 0.001 | 1.781 | 7.145 |
| RFR | 0.981 | −0.045 | 0.246 | 0.061 | 0.992 | 0.005 | 0.144 | 0.881 |
| KRR | 0.998 | 0.002 | 0.196 | 0.058 | 0.983 | 0.019 | 0.224 | 1.588 |
| GPR | 0.998 | −0.002 | 0.029 | 0.068 | 0.996 | 0.008 | 0.113 | 1.104 |
| SVR | 0.993 | −0.025 | 0.128 | 0.067 | 0.892 | −0.245 | 0.383 | 0.845 |
| S3 all bands + ratios | ||||||||
| RLR | 0.991 | 0.006 | 0.474 | 0.164 | 0.962 | −0.023 | 0.460 | 1.853 |
| RFR | 0.998 | −0.007 | 0.126 | 0.038 | 0.992 | −0.019 | 0.114 | 0.168 |
| KRR | 0.998 | 0.009 | 0.037 | 0.046 | 0.989 | −0.008 | 0.131 | 2.264 |
| GPR | 0.999 | 0.012 | 0.014 | 0.035 | 0.996 | −0.012 | 0.072 | 0.556 |
| SVR | 0.998 | 0.004 | 0.027 | 0.054 | 0.995 | −0.023 | 0.095 | 0.334 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruescas, A.B.; Hieronymi, M.; Mateo-Garcia, G.; Koponen, S.; Kallio, K.; Camps-Valls, G. Machine Learning Regression Approaches for Colored Dissolved Organic Matter (CDOM) Retrieval with S2-MSI and S3-OLCI Simulated Data. Remote Sens. 2018, 10, 786. https://doi.org/10.3390/rs10050786
Ruescas AB, Hieronymi M, Mateo-Garcia G, Koponen S, Kallio K, Camps-Valls G. Machine Learning Regression Approaches for Colored Dissolved Organic Matter (CDOM) Retrieval with S2-MSI and S3-OLCI Simulated Data. Remote Sensing. 2018; 10(5):786. https://doi.org/10.3390/rs10050786
Chicago/Turabian StyleRuescas, Ana Belen, Martin Hieronymi, Gonzalo Mateo-Garcia, Sampsa Koponen, Kari Kallio, and Gustau Camps-Valls. 2018. "Machine Learning Regression Approaches for Colored Dissolved Organic Matter (CDOM) Retrieval with S2-MSI and S3-OLCI Simulated Data" Remote Sensing 10, no. 5: 786. https://doi.org/10.3390/rs10050786
APA StyleRuescas, A. B., Hieronymi, M., Mateo-Garcia, G., Koponen, S., Kallio, K., & Camps-Valls, G. (2018). Machine Learning Regression Approaches for Colored Dissolved Organic Matter (CDOM) Retrieval with S2-MSI and S3-OLCI Simulated Data. Remote Sensing, 10(5), 786. https://doi.org/10.3390/rs10050786