Centimetric Accuracy in Snow Depth Using Unmanned Aerial System Photogrammetry and a MultiStation
Abstract
:1. Introduction
2. The Case Study
2.1. UAS Flights
2.2. MultiStation Scans
2.3. Manual Probing
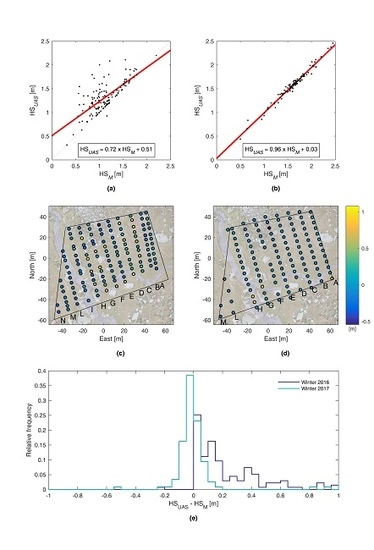
3. Results
3.1. UAS Photogrammetric Blocks: Processing
3.2. UAS vs. MultiStation
3.3. UAS vs. Manual Probing
4. Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- DeWalle, D.R.; Rango, A. Principles of Snow Hydrology; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Fierz, C.; Armstrong, R.; Durand, Y.; Etchevers, P.; Greene, E.; McClung, D.; Nishimura, K.; Satyawali, P.; Sokratov, S. The International Classification for Seasonal Snow on the Ground; Technical Report, IHP-VII Technical Documents in Hydrology N 83, IACS Contribution N 1; UNESCO/IHP: Paris, France, 2009. [Google Scholar]
- Avanzi, F.; De Michele, C.; Ghezzi, A.; Jommi, C.; Pepe, M. A processing-modeling routine to use SNOTEL hourly data in snowpack dynamic models. Adv. Water Resour. 2014, 73, 16–29. [Google Scholar] [CrossRef]
- Morin, S.; Lejeune, Y.; Lesaffre, B.; Panel, J.M.; Poncet, D.; David, P.; Sudul, M. An 18-yr long (1993–2011) snow and meteorological dataset from a mid-altitude mountain site (Col de Porte, France, 1325 m alt.) for driving and evaluating snowpack models. Earth Syst. Sci. Data 2012, 4, 13–21. [Google Scholar] [CrossRef]
- Johnson, J.B.; Marks, D. The detection and correction of snow water equivalent pressure sensor errors. Hydrol. Process. 2004, 18, 3513–3525. [Google Scholar] [CrossRef]
- López Moreno, J.I.; Fassnacht, S.R.; Beguería, S.; Latron, J.B.P. Variability of snow depth at the plot scale: Implications for mean depth estimation and sampling strategies. Cryosphere 2011, 5, 617–629. [Google Scholar] [CrossRef] [Green Version]
- Grünewald, T.; Lehning, M. Are flat-field snow depth measurements representative? A comparison of selected index sites with areal snow depth measurements at the small catchment scale. Hydrol. Process. 2015, 29, 1717–1728. [Google Scholar] [CrossRef]
- López Moreno, J.I.; Revuelto, J.; Fassnacht, S.R.; Azorín-Molina, C.; Vicente-Serrano, S.M.; Morán-Tejeda, E.; Sexstone, G.A. Snowpack variability across various spatio-temporal resolutions. Hydrol. Process. 2015, 29, 1213–1224. [Google Scholar] [CrossRef]
- Helbig, N.; van Herwijnen, A. Subgrid parameterization for snow depth over mountainous terrain from flat field snow depth. Water Resour. Res. 2017. [Google Scholar] [CrossRef]
- Malek, S.A.; Avanzi, F.; Brun-Laguna, K.; Maurer, T.; Oroza, C.A.; Hartsough, P.C.; Watteyne, T.; Glaser, S.D. Real-time Alpine measurement system using wireless sensor networks. Sensors 2017, 17, 2583. [Google Scholar] [CrossRef] [PubMed]
- Kattelmann, R. Spatial variability of snow-pack outflow at a site in Sierra Nevada, USA. Ann. Glaciol. 1989, 13, 124–128. [Google Scholar] [CrossRef]
- Schweizer, J.; Kronholm, K.; Bruce Jamieson, J.; Birkeland, K.W. Review of spatial variability of snowpack properties and its importance for avalanche formation. Cold Reg. Sci. Technol. 2008, 51, 253–272. [Google Scholar] [CrossRef]
- Grünewald, T.; Schirmer, M.; Mott, R.; Lehning, M. Spatial and temporal variability of snow depth and ablation rates in a small mountain catchment. Cryosphere 2010, 4, 215–225. [Google Scholar] [CrossRef]
- Scipión, D.; Mott, R.; Lehning, M.; Schneebeli, M.; Berne, A. Seasonal small-scale spatial variability in alpine snowfall and snow accumulation. Water Resour. Res. 2013, 49, 1446–1457. [Google Scholar] [CrossRef]
- Bavera, D.; De Michele, C. Snow water equivalent estimation in the Mallero basin using snow gauge data and MODIS images and fieldwork validation. Hydrol. Process. 2009, 23, 1961–1972. [Google Scholar] [CrossRef]
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote sensing of snow—A review of available methods. Int. J. Remote Sens. 2012, 33, 4094–4134. [Google Scholar] [CrossRef]
- Sturm, M. White water: Fifty years of snow research in WRR and the outlook for the future. Water Resour. Res. 2015, 51, 4948–4965. [Google Scholar] [CrossRef]
- Jörg, P.; Fromm, R.; Sailer, R.; Schaffhauser, A. Measuring snow depth with a terrestrial laser ranging system. In Proceedings of the International Snow Science Workshop, Telluride, CO, USA, 1–6 October 2006; pp. 452–460. [Google Scholar]
- Jaakkola, A.; Hyyppä, J.; Puttonen, E. Measurement of snow depth using a low-cost mobile laser scanner. IEEE Geosci. Remote Sens. Lett. 2014, 11, 587–591. [Google Scholar] [CrossRef]
- Prokop, A.; Schirmer, M.; Rub, M.; Lehning, M.; Stocker, M. A comparison of measurement methods: Terrestrial laser scanning, tachymetry and snow probing for the determination of the spatial snow-depth distribution on slopes. Ann. Glaciol. 2008, 49, 210–216. [Google Scholar] [CrossRef]
- Grünewald, T.; Stötter, J.; Pomeroy, J.W.; Dadic, R.; Baños, I.M.; Marturiá, J.; Spross, M.; Hopkinson, C.; Burlando, P.; Lehning, M. Statistical modelling of the snow depth distribution in open alpine terrain. Hydrol. Earth Syst. Sci. 2013, 17, 3005–3021. [Google Scholar] [CrossRef]
- Revuelto, J.; Vionnet, V.; López-Moreno, J.I.; Lafaysse, M.; Morin, S. Combining snowpack modeling and terrestrial laser scanner observations improves the simulation of small scale snow dynamics. J. Hydrol. 2016, 533, 291–307. [Google Scholar] [CrossRef]
- Bühler, Y.; Marty, M.; Egli, L.; Veitinger, J.; Jonas, T.; Thee, P.; Ginzler, C. Snow depth mapping in high-alpine catchments using digital photogrammetry. Cryosphere 2015, 9, 229–243. [Google Scholar] [CrossRef]
- Nolan, M.; Larsen, C.; Sturm, M. Mapping snow depth from manned aircraft on landscape scales at centimeter resolution using structure-from-motion photogrammetry. Cryosphere 2015, 9, 1445–1463. [Google Scholar] [CrossRef]
- Machguth, H.; Eisen, O.; Paul, F.; Hoezle, M. Strong spatial variability of snow accumulation observed with helicopter-borne GPR on two adjacent Alpine glaciers. Geophys. Res. Lett. 2006, 33, L13503. [Google Scholar] [CrossRef]
- Farinotti, D.; Magnusson, J.; Huss, M.; Bauder, A. Snow accumulation distribution inferred from time-lapse photography and simple modelling. Hydrol. Process. 2010, 24, 2087–2097. [Google Scholar] [CrossRef]
- Parajka, J.; Haas, P.; Kirnbauer, R.; Jansa, J.; Blöschl, G. Potential of time-lapse photography of snow for hydrological purposes at the small catchment scale. Hydrol. Process. 2012, 26, 3327–3337. [Google Scholar] [CrossRef]
- Adams, M.S.; Bühler, Y.; Fromm, R. Multitemporal accuracy and precision assessment of unmanned aerial system photogrammetry for slope-scale snow depth maps in Alpine terrain. Pure Appl. Geophys. 2017. [Google Scholar] [CrossRef]
- Thamm, H.; Judex, M. The “low cost drone”—An interesting tool for process monitoring in a high spatial and temporal resolution. In Proceedings of the ISPRS Commission VII Mid-Term Symposium “Remote Sensing from Pixels to Processes”, Enschede, The Netherlands, 8–11 May 2006; pp. 140–144. [Google Scholar]
- Newcombe, L. Green fingered UAVs. In Unmanned Vehicle; 2007. [Google Scholar]
- Grenzdörffer, G.; Engel, A.; Teichert, B. The photogrammetric potential of low-cost UAVs in forestry and agriculture. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 31, 1207–1214. [Google Scholar]
- Gini, R.; Passoni, D.; Pinto, L.; Sona, G. Use of unmanned aerial systems for multispectral survey and tree classification: A test in a park area of northern Italy. Eur. J. Remote Sens. 2014, 47, 251–269. [Google Scholar] [CrossRef]
- Niethammer, U.; Rothmund, S.; James, M.; Travelletti, J.; Joswig, M. UAV-based remote sensing of landslides. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 496–501. [Google Scholar]
- Molina, P.; Colomina, I.; Victoria, T.; Skaloud, J.; Kornus, W.; Prades, R.; Aguilera, C. Searching lost people with UAVS: The system and results of the CLOSE-SEARCH project. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 441–446. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Pagliari, D.; Rossi, L.; Passoni, D.; Pinto, L.; De Michele, C.; Avanzi, F. Measuring the volume of flushed sediments in a reservoir using multi-temporal images acquired with UAS. Geomat. Nat. Hazards Risk 2017, 8, 150–166. [Google Scholar] [CrossRef]
- Berni, J.A.; Zarco-Tejada, P.J.; Suárez, L.; Fereres, E. Thermal and narrowband multispectral remote sensing for vegetation monitoring from an unmanned aerial vehicle. IEEE Trans. Geosci. Remote Sens. 2009, 47, 722–738. [Google Scholar] [CrossRef] [Green Version]
- Tauro, F.; Porfiri, M.; Grimaldi, S. Surface flow measurements from drones. J. Hydrol. 2016, 540, 240–245. [Google Scholar] [CrossRef]
- Eisenbeiß, H. UAV Photogrammetry. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2009. [Google Scholar]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Tao, T.S.; Hansman, R.J. Development of an In-Flight-Deployable Micro-UAV. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 1742. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Koenderink, J.J.; Van Doorn, A.J. Affine structure from motion. JOSA A 1991, 8, 377–385. [Google Scholar] [CrossRef]
- El-Gayar, M.; Soliman, H.; Meky, N. A comparative study of image low level feature extraction algorithms. Egypt. Inform. J. 2013, 14, 175–181. [Google Scholar] [CrossRef]
- Lingua, A.M.; Marenchino, D.; Nex, F.C. A Comparison between “old and new” feature extraction and matching techniques in photogrammetry. RevCAD J. Geod. Cadastre 2009, 9, 43–52. [Google Scholar]
- Vander Jagt, B.; Lucieer, A.; Wallace, L.; Turner, D.; Durand, M. Snow depth retrieval with UAS using photogrammetric techniques. Geosciences 2015, 5, 264–285. [Google Scholar] [CrossRef]
- De Michele, C.; Avanzi, F.; Passoni, D.; Barzaghi, R.; Pinto, L.; Dosso, P.; Ghezzi, A.; Gianatti, R.; Della Vedova, G. Using a fixed-wing UAS to map snow depth distribution: An evaluation at peak accumulation. Cryosphere 2016, 10, 511–522. [Google Scholar] [CrossRef]
- Bühler, Y.; Adams, M.S.; Bösch, R.; Stoffel, A. Mapping snow depth in alpine terrain with unmanned aerial systems (UASs): Potential and limitations. Cryosphere 2016, 10, 1075–1088. [Google Scholar] [CrossRef]
- Harder, P.; Schirmer, M.; Pomeroy, J.; Helgason, W. Accuracy of snow depth estimation in mountain and prairie environments by an unmanned aerial vehicle. Cryosphere 2016, 10, 2559–2571. [Google Scholar] [CrossRef]
- Lendzioch, T.; Langhammer, J.; Jenicek, M. Tracking forest and open area effects on snow accumulation by unmanned aerial vehicle photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 917. [Google Scholar] [CrossRef]
- Marti, R.; Gascoin, S.; Berthier, E.; de Pinel, M.; Houet, T.; Laffly, D. Mapping snow depth in open alpine terrain from stereo satellite imagery. Cryosphere 2016, 10, 1361–1380. [Google Scholar] [CrossRef] [Green Version]
- Bühler, Y.; Adams, M.S.; Stoffel, A.; Boesch, R. Photogrammetric reconstruction of homogenous snow surfaces in alpine terrain applying near-infrared UAS imagery. Int. J. Remote Sens. 2017, 38, 3135–3158. [Google Scholar] [CrossRef]
- Gindraux, S.; Boesch, R.; Farinotti, D. Accuracy assessment of digital surface models from unmanned aerial vehicles’ imagery on glaciers. Remote Sens. 2017, 9, 186. [Google Scholar] [CrossRef]
- Smith, F.; Cooper, C.; Chapman, E. Measuring Snow Depths by Aerial Photography. In Proceedings of the 35th Annual Meeting, Western Snow Conference, Boise, ID, USA, 18–20 April 1967; pp. 66–72. [Google Scholar]
- Cline, D. Measuring alpine snow depths by digital photogrammetry. Part 1: Conjugate point identification. In Proceedings of the Eastern Snow Conference, Quebec City, QC, Canada, 8–10 June 1993; pp. 265–271. [Google Scholar]
- Cline, D.W. Digital photogrammetric determination of Alpine snowpack distribution for hydrologic modeling. In Proceedings of the Western Snow Conference, Colorado State University, Fort Collins, CO, USA, 18–21 April 1994. [Google Scholar]
- Grimm, D.E. Leica Nova MS50: The world’s first MultiStation. GeoInformatics 2013, 16, 22. [Google Scholar]
- Fagandini, R.; Federici, B.; Ferrando, I.; Gagliolo, S.; Pagliari, D.; Passoni, D.; Pinto, L.; Rossi, L.; Sguerso, D. Evaluation of the Laser Response of Leica Nova MultiStation MS60 for 3D Modelling and Structural Monitoring. In International Conference on Computational Science and Its Applications; Springer: Berlin, Germany, 2017; pp. 93–104. [Google Scholar]
- Federman, A.; Quintero, M.S.; Kretz, S.; Gregg, J.; Lengies, M.; Ouimet, C.; Laliberte, J. UAV photgrammetric workflows: A best practice guideline. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42. [Google Scholar] [CrossRef]
- Painter, T.H.; Berisford, D.F.; Boardman, J.W.; Bormann, K.J.; Deems, J.S.; Gehrke, F.; Hedrick, A.; Joyce, M.; Laidlaw, R.; Marks, D.; et al. The airborne snow observatory: Fusion of scanning lidar, imaging spectrometer, and physically-based modeling for mapping snow water equivalent and snow albedo. Remote Sens. Environ. 2016, 184, 139–152. [Google Scholar] [CrossRef]
- Avanzi, F.; Hirashima, H.; Yamaguchi, S.; Katsushima, T.; De Michele, C. Observations of capillary barriers and preferential flow in layered snow during cold laboratory experiments. Cryosphere 2016, 10, 2013–2026. [Google Scholar] [CrossRef]
- Wever, N.; Würzer, S.; Fierz, C.; Lehning, M. Simulating ice layer formation under the presence of preferential flow in layered snowpacks. Cryosphere 2016, 10, 2731–2744. [Google Scholar] [CrossRef]
- Eiriksson, D.; Whitson, M.; Luce, C.H.; Marshall, H.P.; Bradford, J.; Benner, S.G.; Black, T.; Hetrick, H.; McNamara, P. An evaluation of the hydrologic relevance of lateral flow in snow at hillslope and catchment scales. Hydrol. Process. 2013, 27, 640–654. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration. Snow Measurement Guidelines for National Weather Service Surface Observing Programs; National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 2013. [Google Scholar]
- Mizukami, N.; Perica, S. Spatiotemporal characteristics of snowpack density in the mountainous regions of the Western United States. J. Hydrometeorol. 2008, 9, 1416–1426. [Google Scholar] [CrossRef]
- De Michele, C.; Avanzi, F.; Ghezzi, A.; Jommi, C. Investigating the dynamics of bulk snow density in dry and wet conditions using a one-dimensional model. Cryosphere 2013, 7, 433–444. [Google Scholar] [CrossRef]
- Sturm, M.; Taras, B.; Liston, G.E.; Derksen, C.; Jonas, T.; Lea, J. Estimating snow water equivalent using snow depth data and climate classes. J. Hydrometeorol. 2010, 11, 1380–1394. [Google Scholar] [CrossRef]
- Raleigh, M.S.; Small, E.E. Snowpack density modeling is the primary source of uncertainty when mapping basin-wide SWE with lidar. Geophys. Res. Lett. 2017, 44, 3700–3709. [Google Scholar] [CrossRef]





| Task | Winter 2016 | Winter 2017 |
|---|---|---|
| UAS flights | 12 PM | 12 PM |
| MS surveys | 12 PM to 1 PM | 12 PM to 1 PM |
| Manual probing | 1 PM to 4 PM | 1 PM to 4 PM |
| Flight Season | East (m) | North (m) | Height (m) |
|---|---|---|---|
| Summer 2016 | 0.010 | 0.007 | 0.005 |
| Winter 2016 | 0.017 | 0.010 | 0.004 |
| Winter 2017 | 0.006 | 0.007 | 0.009 |
| Point Cloud (C1) | DSM (C2) | |||||
|---|---|---|---|---|---|---|
| Survey | Mean (m) | St. Dev. (m) | RMSE (m) | Mean (m) | St. Dev. (m) | RMSE (m) |
| Summer 2016 | 0.004 | 0.020 | 0.020 | 0.001 | 0.068 | 0.068 |
| Winter 2016 | 0.026 | 0.025 | 0.036 | 0.041 | 0.056 | 0.069 |
| Winter 2017 | −0.003 | 0.015 | 0.015 | −0.005 | 0.025 | 0.025 |
| Group | Mean (m) | St. Dev. (m) | RMSE (m) |
|---|---|---|---|
| 1 | 0.11 | 0.14 | 0.17 |
| 2 | 0.36 | 0.27 | 0.45 |
| Mean (m) | St. Dev. (m) | RMSE (m) | |
|---|---|---|---|
| With outliers | 0.01 | 0.20 | 0.20 |
| Without outliers | 0.04 | 0.05 | 0.06 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avanzi, F.; Bianchi, A.; Cina, A.; De Michele, C.; Maschio, P.; Pagliari, D.; Passoni, D.; Pinto, L.; Piras, M.; Rossi, L. Centimetric Accuracy in Snow Depth Using Unmanned Aerial System Photogrammetry and a MultiStation. Remote Sens. 2018, 10, 765. https://doi.org/10.3390/rs10050765
Avanzi F, Bianchi A, Cina A, De Michele C, Maschio P, Pagliari D, Passoni D, Pinto L, Piras M, Rossi L. Centimetric Accuracy in Snow Depth Using Unmanned Aerial System Photogrammetry and a MultiStation. Remote Sensing. 2018; 10(5):765. https://doi.org/10.3390/rs10050765
Chicago/Turabian StyleAvanzi, Francesco, Alberto Bianchi, Alberto Cina, Carlo De Michele, Paolo Maschio, Diana Pagliari, Daniele Passoni, Livio Pinto, Marco Piras, and Lorenzo Rossi. 2018. "Centimetric Accuracy in Snow Depth Using Unmanned Aerial System Photogrammetry and a MultiStation" Remote Sensing 10, no. 5: 765. https://doi.org/10.3390/rs10050765
APA StyleAvanzi, F., Bianchi, A., Cina, A., De Michele, C., Maschio, P., Pagliari, D., Passoni, D., Pinto, L., Piras, M., & Rossi, L. (2018). Centimetric Accuracy in Snow Depth Using Unmanned Aerial System Photogrammetry and a MultiStation. Remote Sensing, 10(5), 765. https://doi.org/10.3390/rs10050765