3.1. General Turbine Wake Characteristics
In this section, we present results from large-eddy simulations of the wake flows behind wind turbines operating in neutral ABLs over flat surfaces with different roughness lengths (
= 0.5, 0.05, 0.005, and 0.00005 m). These results are obtained from the simulations using the finest grid resolution (288 × 192 × 96). Spatial distribution of five key turbulence statistics is used to characterize the wind-turbine wakes: time-averaged streamwise velocity
(m s
), normalized velocity deficit
, streamwise turbulence intensity
, added turbulence intensity
, and kinematic shear stress
(m
s
). To have the same mean rotating speed on the turbines in all the cases, the upwind incoming flows have the same wind speed
= 9 m s
at the hub level but different mean wind shears and turbulence intensity levels.
Figure 2 displays the main characteristics of the simulated neutrally-stratified ABLs over the different surface types. These simulated velocity fields are then used as inflows to the wind-turbine wake simulations. As expected, the rougher the surface, the higher the shear and, for the same
, the larger the turbulence intensity and turbulent stresses.
Figure 2.
Vertical profiles of (a) the time-averaged streamwise velocity (m s); (b) the streamwise turbulence intensity ; and (c) the kinematic shear stress (m s) of the incoming ABL flows over flat surfaces with the four different roughness lengths.
Figure 2.
Vertical profiles of (a) the time-averaged streamwise velocity (m s); (b) the streamwise turbulence intensity ; and (c) the kinematic shear stress (m s) of the incoming ABL flows over flat surfaces with the four different roughness lengths.
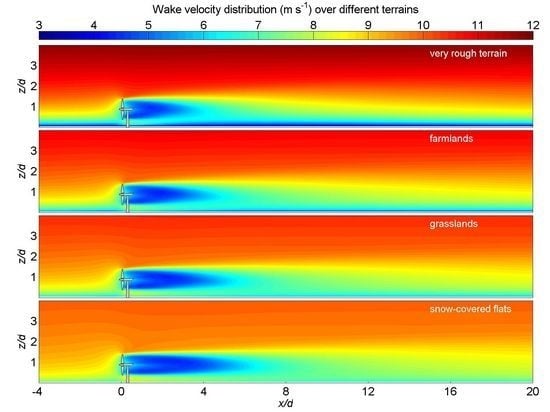
Figure 3 and
Figure 4 display two-dimensional contours of the time-averaged streamwise velocity in a vertical
plane through the center of the turbines at zero span (
y = 0) as well as on different
cross-sectional planes (
= 3, 5, 7, 10, and 15) downstream of the turbines, respectively. To further facilitate the quantitative comparison of the results, both lateral and vertical profiles of the normalized velocity deficit
through the center of the wakes are shown in
Figure 5 for the same selected downstream locations, where
is the time-averaged velocity deficit, and
is the time-averaged streamwise inflow velocity shown in
Figure 2a. As seen in
Figure 3,
Figure 4 and
Figure 5, the simulation results indicate that the upwind flows with different mean wind shears and turbulence intensity levels result in significant differences in the mean velocity distribution of the turbine wakes. In general, a higher level of turbulence in the inflow leads to a smaller wake region (
i.e., faster wake recovery) due to the increased efficiency of the background ABL turbulence to get mixed with and transfer its momentum into the wake.
In
Figure 5, the lateral and vertical profiles of the velocity deficit calculated with respect to the logarithmic incoming wind velocity profiles (shown in
Figure 2a) are approximately axisymmetric, with their axes of symmetry located near the turbine axis. This axisymmetric (particularly two-dimensional Gaussian-like) behavior in the turbine wakes is consistent with previous simulation and experimental results by Rados
et al. [
9], Réthoré
et al. [
11], Chamorro and Porté-Agel [
6], and Chamorro and Porté-Agel [
7]. In
Figure 5, it is shown clearly that the radial distribution of the turbine-induced wakes (
i.e., the width of the axisymmetric distribution) expands with downstream distance due to the enhanced turbulence mixing. Moreover, due to the presence of the ground surface, the axisymmetry in the vertical direction breaks down after about 7 rotor diameters, where the size of the turbulent wakes has grown big enough to reach the surface.
Figure 3.
Contours of the time-averaged streamwise velocity (m s) in the middle vertical plane perpendicular to the turbines installed over flat surfaces with different roughness lengths.
Figure 3.
Contours of the time-averaged streamwise velocity (m s) in the middle vertical plane perpendicular to the turbines installed over flat surfaces with different roughness lengths.
Figure 4.
Contours of the time-averaged streamwise velocity (m s) at the lateral cross-sectional planes of = 3, 5, 7, 10, and 15 for the turbines installed over flat surfaces with four different roughness lengths. The dotted line denotes the rotor region.
Figure 4.
Contours of the time-averaged streamwise velocity (m s) at the lateral cross-sectional planes of = 3, 5, 7, 10, and 15 for the turbines installed over flat surfaces with four different roughness lengths. The dotted line denotes the rotor region.
Figure 5.
Comparison of vertical (a) and lateral (b) profiles of the normalized velocity deficit through the hub level of stand-alone turbines installed on flat surfaces with different roughness lengths.
Figure 5.
Comparison of vertical (a) and lateral (b) profiles of the normalized velocity deficit through the hub level of stand-alone turbines installed on flat surfaces with different roughness lengths.
Figure 6 and
Figure 7 display two-dimensional contours of the streamwise turbulence intensity in a vertical
plane through the center of the turbines at zero span (
y = 0) as well as on different
cross-sectional planes (
= 3, 5, 7, 10, and 15) downstream of the turbines, respectively. From these figures, an obvious enhancement of turbulence intensity is observed in the upper half of the wake. This enhancement is related to intense mechanical production of turbulence kinetic energy associated with the strong shear and momentum flux found at that location. This effect will be further discussed in
Section 3.2. It should be noted that, in all the simulations, the maximum turbulence intensity is found at the top-tip level, where the shear is strongest. However, the exact location and magnitude of the maximum turbulence intensity is clearly affected by the inflow condition. In particular, higher turbulence levels in the incoming flow lead to also larger maximum wake turbulence levels, which occur closer to the turbine for the roughest case (about 2 rotor diameters downwind), compared with the smoothest case (about 5 rotor diameters downwind). This is consistent with the faster overall recovery of the wakes observed in the high background turbulence cases.
Turbulence intensity is commonly used as a surrogate measure of the accumulation of fatigue loads on wind turbines. In turbine wakes, the total turbulence intensity
is composed of the ambient turbulence intensity
from the inflow and the added turbulence
generated by turbines. Here,
is defined as:
Figure 6.
Contours of the streamwise turbulence intensity in the middle vertical plane perpendicular to the turbines installed over flat surfaces with different roughness lengths.
Figure 6.
Contours of the streamwise turbulence intensity in the middle vertical plane perpendicular to the turbines installed over flat surfaces with different roughness lengths.
Figure 7.
Contours of the streamwise turbulence intensity at the lateral cross-sectional planes of = 3, 5, 7, 10, and 15 for the turbines installed over flat surfaces with four different roughness lengths. The dotted line denotes the rotor region.
Figure 7.
Contours of the streamwise turbulence intensity at the lateral cross-sectional planes of = 3, 5, 7, 10, and 15 for the turbines installed over flat surfaces with four different roughness lengths. The dotted line denotes the rotor region.
To investigate quantitatively the turbine-induced turbulence, both lateral and vertical profiles of the added turbulence intensity
through the hub of the turbines are shown in
Figure 8 at three, five, seven, ten, and fifteen rotor diameters downstream of the turbines. As expected, the magnitude of the added turbulence intensities decreases with respect to downwind distance owing to the turbulent mixing effect. The lateral
profiles exhibit a dual-peak pattern with the larger
values near the two side-tip positions at the hub level. For the selected downstream wake positions, a similar enhancement in the added turbulence intensity appears along the vertical direction, and has the maximum near the top-tip level.
In
Figure 8, we find that, below the hub height of the turbines, there is an obvious change in the magnitude of the added turbulence intensity with respect to the four different inflow conditions. In particular, the added turbulence intensity below the hub level becomes smaller as the aerodynamic roughness of the terrain increases. For the roughest terrains, the added turbulence intensity becomes negative in the lower half of the wake, indicating that the wake flow is actually less turbulent than the incoming boundary layer flow at that height. This behavior is consistent with the experimental results reported by Chamorro and Porté-Agel [
6] and Zhang
et al. [
14].
Figure 8.
Comparison of vertical (a) and lateral (b) profiles of the added streamwise turbulence intensity through the hub level of the turbines installed on flat surfaces with different roughness lengths.
Figure 8.
Comparison of vertical (a) and lateral (b) profiles of the added streamwise turbulence intensity through the hub level of the turbines installed on flat surfaces with different roughness lengths.
Figure 9 and
Figure 10 display two-dimensional contours of the kinematic shear stress in a vertical
plane through the center of the turbines at zero span (
y = 0) as well as on different
cross-sectional planes (
= 3, 5, 7, 10, and 15) downstream of the turbines, respectively. From these figures, it is evident that the wake flow is associated with a strong enhancement of the turbulence shear stress
, which has positive values around the upper edge of the wake and negative values around the lower edge. This can be explained by the strong entrainment of the surrounding boundary-layer flow into the wake, which produces a momentum flux in the radial direction towards the wake center (hence leading to positive turbulent stress at the upper edge of the wake and negative one at the lower edge). It should be noted that the magnitude of the momentum flux is larger in the upper part of the wake, where the shear is strongest. Like with the turbulence intensity distribution, the higher background turbulence over the rougher surfaces leads to a more axisymmetric wake distribution, with larger values of the wake turbulent stress, compared with the smoother cases. This higher entrainment flux in more turbulent inflow conditions is consistent with the above-described faster wake recovery in those conditions. From
Figure 9, the position of the maximum turbulence stress is found near the top-tip level and at a distance downstream of the turbine that ranges from about 2 to 5 rotor diameters, coinciding with the location of the maximum turbulence intensity (
Figure 6).
As mentioned earlier, the incoming ABL flows have two important characteristics that can potentially affect the structure of wind-turbine wakes: the ambient turbulence intensity and the mean wind shear. In order to isolate the effect of turbulence intensity from that of wind shear, we have performed an additional simulation using a synthetic inflow velocity field that has the same mean shear as the inflow from Case 1 (roughest surface case) but the turbulence intensity level corresponding to Case 4 (the smoothest surface case). In particular, the synthetic inflow field was constructed by combining the mean velocity profile from the Case 1 inflow with the turbulence velocity fluctuations from the Case 4 inflow. The new simulation case is referred to as Case 5. Vertical profiles of the time-averaged streamwise velocity
(m s
), the streamwise turbulence intensity
, and the kinematic shear stress
(m
s
) for the synthetic inflow velocity field, together with the inflow fields developed over the smoothest (Case 4) and roughest (Case 1) surfaces, are shown in
Figure 11.
Figure 9.
Contours of the kinematic shear stress (m s) in the middle vertical plane perpendicular to the turbines installed over flat surfaces with different roughness lengths.
Figure 9.
Contours of the kinematic shear stress (m s) in the middle vertical plane perpendicular to the turbines installed over flat surfaces with different roughness lengths.
Figure 10.
Contours of the kinematic shear stress (m s) at the lateral cross-sectional planes of = 3, 5, 7, 10, and 15 for the turbines installed over flat surfaces with four different roughness lengths. The dotted line denotes the rotor region.
Figure 10.
Contours of the kinematic shear stress (m s) at the lateral cross-sectional planes of = 3, 5, 7, 10, and 15 for the turbines installed over flat surfaces with four different roughness lengths. The dotted line denotes the rotor region.
Figure 11.
Vertical profiles of (a) the time-averaged streamwise velocity (m s); (b) the streamwise turbulence intensity ; and (c) the kinematic shear stress (m s) of the incoming turbulent boundary layer flows.
Figure 11.
Vertical profiles of (a) the time-averaged streamwise velocity (m s); (b) the streamwise turbulence intensity ; and (c) the kinematic shear stress (m s) of the incoming turbulent boundary layer flows.
Figure 12 and
Figure 13 present profiles (spanwise and vertical) of the normalized velocity deficit
and the added streamwise turbulence intensity
, respectively, through the center of the wake at selected downwind positions. From these figures, it is evident that turbulence intensity has a stronger effect on the structure and characteristics of wind-turbine wakes, compared with that of the mean wind shear alone. In particular, the higher turbulence levels in the incoming flow facilitate turbulent mixing and entrainment (as reflected in the higher entrainment fluxes and turbulence levels in the wake), which in turn enables the wake velocity to recover faster.
Figure 12.
Comparison of vertical (a) and lateral (b) profiles of the normalized velocity deficit through the centerline of the wakes.
Figure 12.
Comparison of vertical (a) and lateral (b) profiles of the normalized velocity deficit through the centerline of the wakes.
Figure 13.
Comparison of vertical (a) and lateral (b) profiles of the added streamwise turbulence intensity through the centerline of the wakes.
Figure 13.
Comparison of vertical (a) and lateral (b) profiles of the added streamwise turbulence intensity through the centerline of the wakes.
In order to assess the sensitivity of the simulation results to grid resolution, a series of additional simulations were performed of Case 1 with four different grid resolutions (see
Table 1). The four cases used a similar grid cell aspect ratio (
:
:
≈ 1.86:1.46:1.00). Contour plots of the time-averaged streamwise velocity are shown in
Figure 14. To provide a more quantitative comparison of the results obtained with the four grid resolutions,
Figure 15 and
Figure 16 show the profiles of the normalized velocity deficit and the added streamwise turbulence intensity (resolved part), respectively. The outcome of these resolution sensitivity tests confirms that our recently-developed LES framework yields velocity deficit results that have little resolution dependence as long as at least seven grid points are used to cover the rotor diameter in the vertical direction, and five points in the spanwise direction. This outcome is consistent with the results reported by Wu and Porté-Agel [
22] in validations of the same LES framework against wind-tunnel measurements.
Figure 14.
Contours of the streamwise velocity obtained from the LESs using different grid resolutions on the (a) and (b) planes.
Figure 14.
Contours of the streamwise velocity obtained from the LESs using different grid resolutions on the (a) and (b) planes.
Figure 15.
Comparison of vertical (a) and lateral (b) profiles of the normalized velocity deficit through the centerline of the wakes.
Figure 15.
Comparison of vertical (a) and lateral (b) profiles of the normalized velocity deficit through the centerline of the wakes.
Figure 16.
Comparison of vertical (a) and lateral (b) profiles of the added streamwise turbulence intensity on the and planes, respectively, through the turbine top-tip level.
Figure 16.
Comparison of vertical (a) and lateral (b) profiles of the added streamwise turbulence intensity on the and planes, respectively, through the turbine top-tip level.
3.2. TKE Budget in a Stand-Alone Turbine Wake
Motivated by the simulation results described above, a detailed analysis of the TKE budget is carried out to investigate how the turbine-induced turbulence is produced and transported around in the turbine wakes, and how the different incoming flows affect the relevant mechanisms.
In a neutral condition, the buoyant effect is negligible and the TKE budget equation can be written as follows:
where the overbar (−) denotes the temporal average, the tilde (∼) represents the LES three-dimensional spatial filtering operation at scale Δ,
is the total TKE,
is the resolved TKE,
is the instantaneous resolved velocity component in the
i-direction,
is its fluctuating component,
is the SGS stress,
is the Kronecker delta, and
R is the residual term. In Equation (
3), the local storage of TKE is close to zero due to quasi-steady flow conditions. Because the SGS stresses are parametrized using the Smagorinsky-based model, the SGS normal stresses (
i.e.,
,
,
) are not available. Therefore, the residual term includes the contribution of viscous dissipation and pressure-correlation effect as well as some contributions of the SGS turbulence to the production, advection and transport of TKE that cannot be computed from LES data. These later contributions, nonetheless, should be relatively small compared with their resolved counterparts.
Figure 17 shows the contours of the TKE budget terms (shear production, advection, turbulent transport, and residual) in the wake of the turbines operating in two different ABL inflow conditions (Case 1 and Case 4). In the figure, it is obvious that the magnitude of the TKE terms is relatively high in the upper part of the turbine wakes, where the TKE production and transport mechanisms are intense. In particular, the level of the shear production is significant at the rotor tip level. This is consistent with the turbulence intensity results in
Figure 6 and
Figure 7 which show high values of the turbulence intensity at that same level. This significant turbulence enhancement is associated with the combination of a strong turbulent stress (see
Figure 9 and
Figure 10) and a large wind shear (see
Figure 5) in the turbine-induced shear layer.
As shown in
Figure 17, part of the TKE generated at the edge of the turbine wakes (which is stronger in the upper edge) is advected by the mean wind. In particular, the mean advection term is negative in the near-wake region, particularly at top-tip level, due to the positive streamwise gradient of TKE, and it becomes positive after the TKE has reached a maximum and starts to decrease with downwind distance in the far wake. These results indicate that the extent of the near-wake region is affected by the incoming flow turbulence and it is situated approximately two and five rotor diameters from the turbine for the high-turbulence and low-turbulence cases, respectively.
Turbulent transport plays also an important role in redistributing the shear-produced TKE away from the shear layer radially, both inwards and outwards, thus contributing to the expansion of the wake. This explains why the turbulent transport term is negative in the center of the shear layer (around the rotor edge level) and positive on both sides (inside and outside).
Figure 17.
Contours of the TKE budget terms (advection, shear production, turbulent transport, and residual) for the stand-alone turbines installed over flat surfaces with the two different roughness lengths: = 0.5 m (a panel) and = 0.00005 m (b panel). All the quantities are normalized by = 1.458 m s.
Figure 17.
Contours of the TKE budget terms (advection, shear production, turbulent transport, and residual) for the stand-alone turbines installed over flat surfaces with the two different roughness lengths: = 0.5 m (a panel) and = 0.00005 m (b panel). All the quantities are normalized by = 1.458 m s.
In Equation (
3), the TKE shear production, advection, and turbulent transport terms contain several components. They can be written as follows:
In order to investigate the relative importance of the above components to the TKE budget,
Figure 18 shows the contours of these components at the lateral cross-sectional plane of
= 3 for the turbine installed over the roughest surface (
i.e., Case 1). From this figure, it is evident that most of the TKE in the wake is generated by two components:
and
. This is consistent with the high shear of the mean velocity in the radial direction (and thus in the vertical and spanwise directions), and the strong associated radial fluxes of momentum (towards the center of the wake). As for the TKE transport mechanisms, it is clear that part of the TKE in the wake is advected by the streamwise component of the mean wind due to the fact that
is much larger than
and
. In the turbulent transport, it is dominated by
and
because the spanwise and vertical velocity fluctuations (
and
) are responsible for the radial transport of TKE.
Figure 18.
Contours of the components of the TKE budget terms at the lateral cross-sectional plane of = 3 for the turbine installed over the roughest flat surface. (a) shear production; (b) advection; and (c) turbulent transport.
Figure 18.
Contours of the components of the TKE budget terms at the lateral cross-sectional plane of = 3 for the turbine installed over the roughest flat surface. (a) shear production; (b) advection; and (c) turbulent transport.