1. Introduction
The clustering problem is a basic research topic in data mining [
1,
2,
3]; it is encountered in a number of academic and practical fields such as text document analysis, web data analysis, image processing, data compression, and bioinformatics. In recent years, we have viewed an increasing number of publications on the models and algorithms of data clustering [
4,
5,
6,
7], since the topic plays an important role in these fields. The task of clustering is to recognize natural groupings in multidimensional data based on certain similarity measures. For example, Euclidean distance is a measurement for evaluating similarities between clusters, which is one of the most frequently used distances in clustering problems. Specifically, given
N objects, one should allocate each object to one of
K clusters with the aim of minimizing the sum of squared Euclidean distances between each object and its corresponding centroid of the cluster. Formally, the problem can be described as follows [
8,
9]:
where
N is the number of patterns, and
K is the number of clusters;
is the location of the
i-th pattern, and
is the center of the
j-th cluster, and it is obtained by the following Equation (2):
where
is the number of patterns in the
j-th cluster, and
is the association weight of pattern
to cluster
j,
i.e.,
is 1 if pattern
i belongs to cluster
j and 0 otherwise.
Generally, the clustering problem is computationally difficult, namely NP-hard [
10], so investigating efficient optimization algorithms to find better clusters is still an important task. The difficulty for designing and improving such algorithms is to propose effective strategies for optimization and to find suitable values of control parameters. Over the last several decades, a wide variety of algorithms and improvements have been presented and analyzed, which are mainly divided in two kinds: hierarchical methods and partitional methods. The
k-means algorithm [
11] is a basic and well-known partitional method. It starts from
k random positions (centroids) and iterates by updating these centroids until they are no longer moved. The algorithm aims to minimize an objective function, which can be described as follows:
where
is the location of the
i-th pattern, and
is the
k-th centroid. This method is easy to handle, but it often converges to a local optimum, so the quality of results highly depends on the initialization positions.
In order to overcome this issue, an alternative approach is swarm-based or metaheuristic-based optimization algorithms, where the genetic algorithm [
12,
13,
14], particle swarm optimization [
15,
16,
17], and the Artificial Bee Colony (ABC) algorithm [
18,
19] are typical ones. Very recently, some new metaheuristic algorithms have been proposed, such as Monarch Butterfly Optimization (MBO) [
20], Elephant Herding Optimization (EHO) [
21], and Animal Migration Optimization algorithm (AMO) [
22]. Among these, the AMO algorithm, proposed by Li
et al., is an efficient one [
22]. Recent studies have shown that the AMO algorithm is good at solving many numeric optimization problems, and it performs well on benchmark instances. These metaheuristic-based algorithms have shown excellent performance on solving many optimization problems [
23,
24,
25,
26]. They can always achieve good solutions compared to other heuristic algorithms. Metaheuristic-based algorithms have also been employed to deal with clustering problems [
27,
28,
29,
30,
31,
32], since such problems are naturally optimization problems.
In addition, information entropy is a good measure for data clustering, and it is often used as a heuristic. To cluster high-dimensional objects in subspaces and determine the importance of each dimension, Jing
et al. [
33] proposed a method that combines the weight entropy into the objective function to be minimized, and they also introduced an extra step to compute the contribution of each dimension to each cluster. Furthermore, information entropy was used for determining the optimal number of clusters. Liang
et al. [
34] proposed an approach to measure within-cluster entropy and between-cluster entropy with the aim of determining the number of clusters in a given data set effectively. Cheung and Jia [
35] investigated clustering on mixed data composed of numerical and categorical attributes, and proposed an iterative clustering algorithm. To analyze similarities between objects, they provided a method to estimate the significance of categorical attributes using information theory, and then showed that the algorithm can determine the number of clusters automatically without prefixing control parameters.
Though there are several clustering algorithms that employ information entropy to analyze similarities of clusters, there are rare algorithms that use entropy as heuristic information for optimization. In this paper, we propose an information entropy-based AMO algorithm for solving clustering problems. The key feature of the algorithm is that a new migration method as well as a new population updating method controlled by information entropy is proposed. The original migration method is designed for common optimization problems, but the clustering data possess their own distribution, and values of attributes always have cluster properties, so the new migration method employs entropy heuristics to control the searching direction of each attribute, and a similar strategy is also incorporated into our population updating method. We perform intensive experiments on benchmark instances. Experimental results show that our new approach can find better clustering results compared to other approaches presented recently, and further indicate that our new approach accelerates convergence speed of optimization.
The remainder of this paper is organized as follows: In
Section 2, we briefly review the AMO algorithm, and the entropy-based AMO algorithm for clustering problems is introduced in
Section 3. Benchmarks for evaluating algorithms and experimental results are given in
Section 4. Finally, conclusions are provided in
Section 5.
2. The AMO Algorithm
In this section, we briefly introduce the AMO algorithm. The AMO algorithm is a swarm-based algorithm inspired by the migration phenomenon of animals. In the algorithm, individuals are regarded as positions of animals, and positions can be moved by mainly two operations: animal migration and population updating. The operation of animal migration simulates behaviors of animal groups moving from the current area to a new area. New positions of individuals will be produced according to the direction of animal migration, where three migration rules are considered: Individuals move towards the same direction as their neighboring individuals; individuals remain near their neighboring individuals; and individuals avoid collisions with their neighboring individuals. Using the three migration rules, a probability approach is introduced to yield new positions of individuals. The algorithm begins with a randomly initialization population, which is comprised of
NP feature vectors with
dimensions, which can be stated as follows:
where
and
are the maximum value and the minimum value of the
j-th dimension.
is the
j-th dimension value of the
i-th individual in the initialization population, and
is a uniformly random number between 0 and 1,
i = 1, …,
NP and
j = 1, …,
.
After producing the initialization population, animal migration and population updating operations are performed iteratively. During the animal migration, the individuals are supposed to move to new positions according to the positions of their neighboring individuals, which can be described as follows:
where
is the
j-th dimension value of the
i-th individual in the current population
G, and
is the
j-th dimension value of the
i-th individual in the new population
G + 1;
is the
j-th dimension value of the neighboring individual of
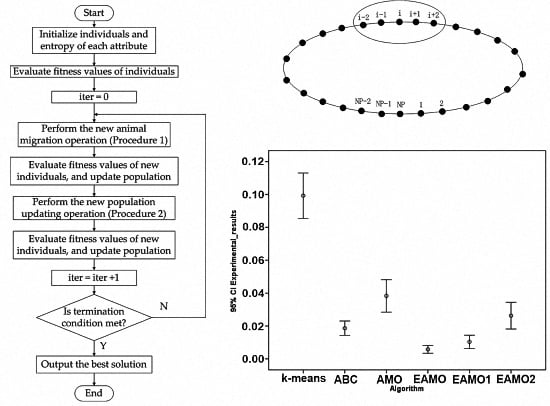
, which is defined using a ring topology scheme illustrated in
Figure 1. In AMO, Li
et al. [
22] employ the four nearest individuals and the
i-th individual itself for each dimension as its neighborhood and choose one individual in the neighborhood randomly as
. As an example,
Figure 1 shows the neighborhood of
if
i-th individual is
. For the
j-th dimension,
is selected from the (
i − 2)-th individual, the (
i − 1)-th individual, the
i-th individual, the (
i + 1)-th individual, and the (
i + 2)-th individual.
is a random number produced by a Gaussian distribution with
N (0, 1).
The population updating simulates how animals leave the group and new individuals join in the new population, as Equation (6) describes:
where
is the
j-th dimension value of the individual to be updated, which is chosen randomly in the current population; moreover, different from
,
is the
j-th dimension value of another random individual, and
is the
j-th dimension value of the best individual that has been found.
and
are two uniformly random numbers between 0 and 1. The algorithm makes the assumption that the number of animals in the population remains unchanged. Therefore, in the updating, it replaces some of the animals with new individual according to a probability
, which is related to the fitness of individuals and can be calculated as follows:
where
is the probability value of the
i-th individual,
NP is the number of the individuals in the population, and
is the sequence number of the fitness of
i-th individual after being sorted by their fitness in descending order, where
i = 1, 2, …,
NP. According to Equation (7),
is 1 if the
i-th individual is of the best fitness, whereas
is 1/
NP if the
i-th individual has the worst fitness.
| Algorithm 1. Animal Migration Optimization (AMO) algorithm |
| 1 begin |
| 2 set the generation counter ; and randomly initialize individuals denoted as () with dimensions. |
| 3 evaluate the fitness for each individual. |
| 4 while stopping criteria is not satisfied do |
| 5 for i = 1 to do |
| 6 for j = 1 to do |
| 7 |
| 8 end for |
| 9 end for |
| 10 for i = 1 to do |
| 11 evaluate the fitness of the offspring , let if is better than |
| 12 end for |
| 13 select randomly () |
| 14 for i = 1 to do |
| 15 for j = 1 to do |
| 16 if then |
| 17 |
| 18 end if |
| 19 end for |
| 20 end for |
| 21 for i = 1 to do |
| 22 evaluate the fitness of the offspring , let if is better than |
| 23 end for |
| 24 memorize the best solution achieved so far |
| 25 end while |
| 26 end |
For each individual and each dimension, a uniformly random number, denoted by
between 0 and 1 will be produced as the probability to determine whether the individual is reserved or is replaced by a new individual. Therefore, individuals with better fitness will be reserved with higher probability in the next generation, while those with worse fitness will probably be replaced by new individuals. Moreover, the animal with best position will be retained in the next generation. The entire AMO algorithm is described in Algorithm 1 [
22].
3. The Information Entropy-Based AMO
In this section, we present a modified AMO algorithm. The original AMO algorithm is good at global searching and local searching, and can lead to a satisfactory solution for numeric optimization. However, the data clustering problem is quite different from the benchmarks of numeric optimization problems, as it is easy to see that data in a clustering problem usually has its own distributions. To adapt the AMO algorithm for data clustering, we investigate inherent features and propose an entropy-based AMO algorithm.
3.1. Attribute Information Entropy
It is clear that data in a clustering problem is a collection of points in a multi-dimensional space. In the general case, those points are not randomly positioned, so an attribute in the data may obey a certain distribution. Therefore, it is more reasonable to use different strategies according to the distribution of the attribute rather than to use a single strategy. Information entropy can be used to evaluate the disorder degree of a stochastic variable, so it is a suitable measure of attributes to evaluate their distribution. We will discuss information entropy of attributes in this subsection.
We use the method proposed by Shannon [
36] to calculate information entropy, which is usually called Shannon’s entropy. Shannon’s entropy is used widely in many information measures. Given a clustering data set, we record the number of attributes as
D, and the number of classes (centroids) as
k first. Then, to evaluate Shannon’s entropy value, we use
to denote entropy of the
i-th attribute, and discretize the attribute values, where each value is approximated to its nearest integer, and then calculate the
i-th attribute entropy as follows:
where
is the minimum integer, and
is the maximum integer after discretization of attribute values.
is the percentage of the
j-th integer of the attribute. Because attribute entropy will be used to control the migration process of the animal population, which will be discussed in the next subsection, we use the maximum possible entropy of the
i-th attribute to normalize Shannon’s entropy
. The maximum possible entropy of the
i-th attribute, denoted as
, can be calculated as follows:
Finally, the normalized entropy of the
i-th attribute
can be described as
where
and
is obtained from Equations (9) and (10), respectively. In the case that
, we will set
to 1. Thus, a normalized information entropy vector
can be obtained and
.
3.2. The New Animal Migration Method
In this subsection, we present our new migration method. In the original AMO algorithm, an individual may move towards one of its neighbors or move away from the neighbor in the migration operation. This method guarantees diversification of the population. To enhance the convergence speed of the migration step and to improve the effectiveness of global searching, we propose a new method by using an alternative route, where two strategies are employed for migration. One is the original method, where a neighbor is picked up with the method used in the original AMO [
22]. The other is newly proposed. It selects
S individuals randomly from the current population (
), and the best one among those
S individuals will be picked up as a reference individual, denoted as
. Usually, we set
S to 5. This reference individual as well as the selected neighbor are taken as candidate migration directions, rather than only moving towards their neighbors. Migration direction (moving according to the reference individual or according to the neighbor) is controlled by a randomized approach. To balance the efforts between diversification of the population and convergence speed, information entropy is used here to make decisions. An attribute with large information entropy implies that values of it are uncertain and disordered; thus, searching on this attribute converges slowly, so we accelerate convergence on this attribute by moving it according to the position of the global reference individual with a higher probability than attributes with lower information entropy. Therefore, we present the new migration method as Procedure 1.
In Procedure 1, same as the original method, is the current position of the i-th individual, and is the current position of the selected neighbor. The selection method is the same as the original AMO; NP is the number of the individuals in the population, and is the dimension of individuals; is a random number produced by a Gaussian distribution with N (0, 1). Different from the original one, dimensions of an individual are not only processed by its neighbor and may also be processed with , where attribute entropy controls the direction. will be used if (a uniformly distribution random number between 0 and 1) is smaller than the normalized entropy of the attribute. Otherwise, the individual will move towards or away from .
| Procedure 1. The new animal migration operation |
| for i = 1 to do |
| Select the best one from S random individuals as |
| for j = 1 to do |
| if then |
| |
| else |
| |
| end if |
| end for |
| end for |
3.3. The New Population Updating Method
During the population updating of AMO, animals will be replaced by a new individual with a probability approach, and the new individual is produced by Equation (6). To further enhance the convergence speed, we propose a new method to decide the manner of producing new individuals, using an attribute entropy similar to the method of our migration method. Two updating manners are involved in the method: moving towards the best individual and moving towards both the best individual and a random individual. Attributes with a higher entropy will probably move close to those of the best individual. The details of the method are shown as follows:
| Procedure 2. The new population updating operation |
| select randomly integers |
| for i=1 to do |
| for j=1 to do |
| if then |
| if then |
| |
| else |
| |
| end if |
| end if |
| end for |
| end for |
where
NP is the number of the individuals in the population, and
is the dimension of individuals;
and
are both random numbers between 0 and 1 with uniform distribution.
,
, and
are random numbers between 0 and 1 to control the convergence speed.
3.4. The Entire Algorithm for Solving Clustering Problems
With discussions and newly proposed strategies in the above subsections, we present our Entropy-based Animal Migration Optimization (EAMO) combining both the new migration method and the new population updating method.
For solving clustering problems by the EAMO, initializing the population is the first operation. During this process, we set an initial population with NP animal individuals where an individual is a vector with length = , where D is the number of attributes of the input dataset, and K is the number of clustering centroids. Positions of K clustering centroids are encoded into the vector, where the first centroid corresponds to the first D elements, and the second centroid corresponds to the second D elements, and so on. Each value in the initial individual vector is produced randomly and uniformly between the maximum value and the minimum value of the corresponding attribute in the input data set. After initialization of population, the EAMO performs optimization iteratively, where Equation (3) is used to evaluate fitness of individuals, until the stopping criterion is satisfied. The detailed description of the algorithm framework is listed as follows.
As is shown in Algorithm 2, it starts from generating initial individuals randomly and uniformly in the ranges of attributes from the input data set, and it then calculates the normalized entropy vector
. Afterwards, the algorithm performs optimization iteratively, where the proposed entropy-based migration operation and population updating operation are employed. Attributes will be updated by the population updating operations with probability
Pa, which is the same as the original AMO algorithm. After each migration of an individual, we calculate the fitness of the new location by Equation (3) in
Section 1. The new location will replace the current one if the new fitness is better than that of the old location. Identical to the migration operation, new better individuals will replace old ones after each population’s updating step. In addition, the best individual found so far will be recorded after all individuals are processed by migration and population updating operations. The algorithm terminates if it achieves the maximum number of iterations, which is the same as the original AMO. The flowchart of the information entropy-based AMO algorithm is shown is
Figure 2.
| Algorithm 2. Information Entropy-based Animal Migration Optimization (EAMO) algorithm |
| 1 begin |
| 2 evaluate the information entropy for attributes, and calculate the entropy vector |
| 3 set the generation counter , and randomly initialize individuals denoted as () |
| 4 evaluate the fitness for each individual in the population |
| 5 while stopping criteria is not satisfied do |
| 6 perform the new animal migration operation (Procedure 1) |
| 7 for i = 1 to do |
| 8 evaluate the fitness of the offspring , let if is better than |
| 9 end for |
| 10 perform the new population updating operation (Procedure 2) |
| 11 for i = 1 to do |
| 12 evaluate the fitness of the offspring , let if is better than |
| 13 end for |
| 14 memorize the best solution achieved so far |
| 15 end while |
| 16 end |