1. Introduction
Harvested lettuce heads should be stored at 0°C until marketed or used [
1]. Research has shown that the shelf life of lettuce stored at 0°C is 21 - 28 days, but only about 14 days when stored at 5°C [
2]. Pre-cooling and maintaining lettuce at low temperatures, without interruption, is one of the most important factors for prolonging post-harvest shelf life and quality. Shelf life of field-grown lettuce was prolonged by rapid (vacuum) cooling immediately following harvest [
3]. If pre-cooled lettuce is left outdoors at an air temperature of approximately 21°C, the core temperature can go from 0.6°C to 10°C within the same day [
4]. Greenhouse-grown butterhead lettuce is more perishable than field-grown iceberg lettuce [
5]. Our preliminary results indicated that vacuum cooling improved the shelf life of commercially harvested greenhouse lettuce [
6].
Temperature fluctuations during post-harvest handling and storage also influence shelf life, and it is desirable to be able to predict the remaining shelf life (RSL) for a box of lettuce. For this reason, some type of device was necessary to record temperatures after harvest. There are two general approaches. First, time-temperature indicators (TTI) may be used to monitor temperatures and to predict shelf life. Three types of TTI for temperature-sensitive foods [
7] were available based on; the melting point of a chemical mixture (e.g. 3M Monitor Mark), an enzymatic reaction (e.g. Vitsab TTI tags), or a polymerization reaction (e.g. LifeLines FreshCheck indicators). Some of these consumer readable TTI tags were evaluated with greenhouse-grown lettuce in a previous study, and Vitsab was found to be most suitable for lettuce [
8]. There are certain problems that need to be corrected before TTI can be used [
9]. For example, manual activation of the TTIs may cause variability in the mixing of the lipid substrate and the enzyme. A machine was designed to activate the TTIs automatically and uniformly in large-scale applications. Even more critical, the activation energy of food and the TTI must be identical, often requiring thorough experimentation. Secondly, a recording device such as a portable data logger can be placed inside a box of lettuce, and temperature records of shipping conditions can be retrieved at various points along the distribution chain. The total shelf life (TSL) of a lettuce head consists of the total number of remaining marketable days: the number of days in storage until the present, plus the RSL which consists of a sum of unknown days into the future. If the overall response of a product to variable storage temperature scenarios can be modeled, it should be possible to use measurements to a given date during the storage period to predict what will occur under assumed future conditions. However, the interactions of temperature and time are complex and difficult to model.
Methods to model and predict biological functions are often difficult due to non-linear responses and complicated interactions among input factors. A new approach, neural network (NN) modeling, has been applied to predict biological functions. NN models have been used for different predictions: canopy photosynthesis [
10], shelf life of meat products [
11], pepper fruit coloration [
12], and pepper weekly yields [
13]. There is no literature reporting the use of NNs to predict shelf life of greenhouse-grown lettuce. The objective of this study was to develop models for predicting RSL of greenhouse-grown lettuce. The data used were from experimental and commercial harvests involving a wide range of pre-harvest conditions and post-harvest temperature fluctuation. Several NN models were established and validated against observed shelf lives. Regression analysis was also used as a comparison.
2. Description of Neural Network
The mathematical description of 2-stage backward propagation neural networks (BPNN) consists of definition of shelf life, structure of generic BPNN, heuristic approaches, and application of NN model for shelf life prediction. The theory and applications of NNs were described by Baughman and Liu [
14].
The definition of shelf life. We collected data of total shelf lives from a number of units of lettuce grown experimentally or commercially. Each unit (box) of lettuce has its own history of average daily temperatures. In this study, shelf life is defined as average shelf life (days) of a box of lettuce with 12-24 heads. The criteria for determining shelf life must be consistent for all the units and all sources of harvest. Given this data, we are required to build a model to predict the RSL. The question is “For this unit of produce with known daily average temperature history up-to-today, what RSL (days) can be expected under various scenarios of future temperatures?”
G
eneric BPNN. Generic NN models for modeling RSL can be expressed as a function of the product of a weight matrix
W and input vector
T,
where
W is a resulting BPNN weight matrix,
T represents the temperature history, and RSL is the remaining shelf life. The number of points of temperature data in a given unit is the same as the number of days of total shelf life, and each unit has its own total shelf life. The dimension of input vector
T (the number of input nodes) is fixed in a given BPNN model. In order to accommodate the varying number of total shelf lives, the input vector
T was the average daily temperature for each unit. For example, a maximum of 18 daily temperature inputs are possible for a box of lettuce observed having 18 days of shelf life.
If the temperature history of a unit has a total shelf life of n days, the daily temperatures are t(1), t(2), …, t(c), …, t(n). The c in t(c) indicates the current day (“today”) as it moves from t(1) to t(n) along the time axis. The components of vector T, i.e. the input nodes for current day (c), can be assigned as follows.
Input node
fs (future sum): the sum of daily temperatures from tomorrow (
c+1) to end of shelf life (
n). This node
fs covers the temperatures of the RSL of (
n-
c) days.
Input node
fa (future average): the average daily temperature of the remaining days (
n-
c).
Input nodes
pm: one node for each of the previous
m days counting back from day
c: For example, If
m=4 days, then we are using
t(
c),
t(
c-1),
t(
c-2) and
t(
c-3) as inputs.
Input node
ps (prior sum): the sum of daily temperatures prior to day (
c-(
m-1)).
The output node, RSL, for a given day
c is simply described as:
This design is one of numerous possibilities, and allocating the up-to-date temperatures into aggregates of nodes (i.e. pm) is an art. In our design of nodes pm, we emphasize the details of temperatures in the last m days (i.e. immediately before current day (c)), assuming that the last m days of temperature may be most important. We used a summation (ps) as a single node for the temperatures prior to day (c-(m-1)).
Heuristics. NN models are established by learning from examples (i.e. available data set), but they can not provide in-depth solutions (i.e. no explanation capacity). On the other hand, knowledge-based expert systems can not easily process information from real-life, unpredictable data. A hybrid structure of expert systems and neural networks has been proposed and implemented in bioprocessing and chemical engineering [
14] (section 6.1 Introduction to Expert Networks, pp. 365-369). The knowledge gained from those studies using TTIs in postharvest handling provides us with the basis for incorporation of the following heuristics into NN models [
8,
9].
Heuristics #1:
The set of nodes of vector T so designed includes fs, fa, pm, and ps. The nodes fs, pm, and ps are simply aggregates of the temperature history in storage. The node fa is introduced in order to allow us to make the RSL prediction more meaningful to end-users. For example, we will be able to interrogate the 2-stage NN model by varying fa in selected intervals of temperature to get the corresponding range of RSL (Heuristics #2, below).
Heuristics #2:
Once the BPNN model is established, we can use its resulting matrix W to determine RSL from equation (1), RSL = f(WT), for a real-life T and given day c. The vector T is expressed as T = (ps, pm, fa, fs).
Here we are immediately faced with the difficulty of unknown fs, since we do not know what the future storage temperatures will be. During the training stage there is no such difficulty, since node fs in vector T is available and well defined from the given historical training data. From the definitions it is obvious that fs, fa, and RSL are mutually dependent via the factor (n-c). Superficially, the node fs is proportional to fa simply by the factor of (n-c). However, the factor (n-c) is the RSL itself which also depends on the temperature history, viz., ps, pm, and fs. Thus we have to introduce the Heuristics #2 as follows.
The future sum (
fs) of temperatures is obtained by an auxiliary BPNN:
where the vector
S is defined as
S = (
ps,
pm,
fa), and the matrix
Y is just another weight matrix obtained from the auxiliary BPNN.
In other words, we are making a good estimate of fs via this auxiliary BPNN using weight matrix Y.
Then we have a heuristic 2-stage BPNN model in order to predict the RSL:
Stage 1; obtain fs using the following:
S = (ps, pm, fa)
fs = f(YS)
Stage 2; input fs into T and obtain RSL by using:
T = (ps, pm, fa, fs)
RSL = f(WT)
In short, we used stage 1 of BPNN to establish the relationship between RSL and fa on the basis of existing historical data. Once the relationship between RSL and fa is established, the RSL can be predicted in stage 2 of BPNN according to a user-specified range of future storage temperature (i.e. fa). In so doing, the predicted RSL is more realistic to commercial practice and tailored to end-user’s specific postharvest conditions. For example, the end-user can ask what the RSL would be if a box of lettuce is placed in a 4°C refrigerator, or what the RSL would be in the retailers’ holding area at 10°C?
Application. In building a 2-stage NN, we separately train BPNN matrices Y (of stage 1) and W (of stage 2) according to the scheme of input vector sets S and T, respectively, for given training data. The same convergence criteria must be used in selecting Y and W. The convergence criteria used in model training includes R-square, root-mean-square and coefficient of variation (CV) for the output node RSL. During model training, we select the same optimal cycle number for both weight matrices Y and W. A special computer program was developed in this study to integrate stage 1 and stage 2 into one operation for end users. Once a model has been trained, the end-user can specify a discrete set of fa values inside a selected temperature interval to obtain corresponding RSL values.
3. Materials and Methods
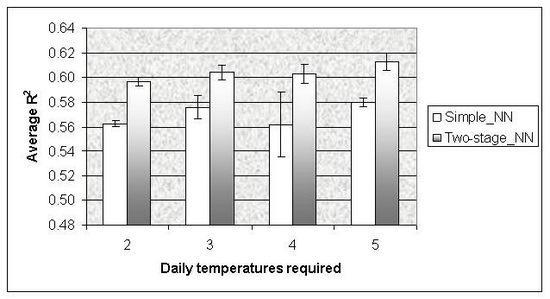
Plant materials. Plants of butterhead lettuce cvs Cortina and Prior were grown under experimental conditions in Agassiz or obtained from a commercial greenhouse in Pitt Meadows, both located within 100 km east of Vancouver, British Columbia, Canada. The experimental plants were harvested from 8 experiments. Butterhead lettuce cv. Prior was used: 6 experiments involved living lettuce (with trimmed roots) and another 2 experiments used butter lettuce (with no roots). These experiments covered various pre-harvest growing conditions and post-harvest temperature combinations (details not shown). Six commercial harvests were obtained directly from the commercial greenhouse. There were 8 experiments involving cvs. Cortina and Prior, including living and butter lettuce. The same postharvest procedures were applied to experimental and commercial materials. Storage experiments were conducted in Agassiz. Living lettuce retains a partial root system, while butter lettuce has the root system removed upon harvest. Each head of living or butter lettuce was wrapped individually with a plastic sleeve. There were 12, 18 or 24 heads in a box. Each box was considered as an experimental unit. There were a total of 198 boxes, including both experimental and commercial harvests. The air temperature of each box was recorded by a portable Hobo Temperature Data Logger, model H08 (Onset Computer Corp. Bourne, MA 02532, USA). Temperatures were averaged over a 24-hour period until shelf life was terminated. Total shelf life of each head is defined as the number of days between date of harvest and the date a lettuce head shows incipient yellowing or decay. Each head of lettuce was visually inspected 3 times a week. The incipient signs of yellowing and decay caused a lettuce head to be considered as unmarketable by the industry in British Columbia. The remaining shelf life (RSL) of each box was the average of 12, 18 or 24 heads, and used as output for shelf life prediction. At the end of each storage experiment, the RSL was back calculated by using the difference between the total shelf life (n) and the number of days in storage until current day (c). In training and testing of simple and 2-stage NN models, a total of 198 data cases were used, representing 198 boxes of lettuce harvested during 1998-2001. Routinely, 80% of 198 cases were randomly selected for training NN models and the remaining 20% were put aside and later used for testing the models. A good fit for NN models was determined by high R2 values and low average errors (%) in testing. Randomization of the selected training cases was repeated at least once. The testing was arbitrarily stopped when R2 of two consecutive results were within 10% or less. Further, the same experimental data used for establishing NN models was used to train regression models, and identical commercial data was used to validate both 2-stage NN and regression models.
Simple NN models. In simple NN modeling daily storage temperatures were used directly to model RSL, while future temperatures were assumed not yet available and ignored. A simple NN model was established by using past daily temperatures with two manipulations. First, the last daily temperature
t(
c) and backward preceding
m daily temperatures (
pm) expressed as
t(
c),
t(
c-1),
t(
c-2), ….,
t(
c-(
m-1)) were used as input
pm nodes for the NN model. Secondly, daily temperatures before
t(
c-
m) were totalled as temperature_prior_sum (
ps). The values of
ps and
pm were used as inputs for modeling RSL. In BPNN, we generated a set of vectors
T from the given data set containing a number of units, in which each unit has its own history of storage temperatures and its own total shelf life (
n). We then performed the training procedures accordingly. For each unit, we ran the given day
c from day 1 to day
n, and generated
n number of
T vectors (e.g. shelf life of 18 days gave 18
T’s; each of 18
T’s had its own RSL as defined by
n-
c). Each vector
T contained the input nodes,
pm and
ps, along with the associated output node, RSL, for a given day
c. The BPNN of RSL consisted of three layers: the input layer, the intermediate layer, and the output layer. The input layer had nodes for
pm and
ps; the output layer had only one node, the RSL. The intermediate layer had a total number of nodes which is less than half of the sum of the input and output nodes. This simple NN procedure was described previously [
12,
13].
Two-stage (2-stage) NN models. In order to overcome the dependence of RSL on unknown future temperatures in simple NN models, a 2-stage NN procedure was employed. Unknown future temperatures were first modeled by an auxiliary NN in stage 1 using historical temperature records, and then combined with daily storage temperatures in a second NN in stage 2 to predict RSL in one operation. In stage 1, we established the temperature matrix S by using ps, pm, and fa, and modeled fs by using S and weight matrix Y (equation (7)). In stage 2, we used the resulting fs as part of temperature matrix T (ps, pm, fa, fs), and RSL was modeled as weight matrix W x T (equation (1)). In short, the auxiliary NN was established to model the relationship between future temperature sum (fs), future temperature average (fa) and RSL. This relationship was used to provide inputs for the second stage of the 2-stage NN to predict RSL.
Regression. The RSL was regressed with daily temperatures by using S-Plus (S-PLUS 6 for Windows, Release 1, Insightful, Seattle, WA). The predicted shelf lives were compared with those of 2-stage NN models. Identical data sets were used for 2-stage NN modeling and regression analysis.