Influence of Tilting Angle on Temperature Measurements of Different Object Sizes Using Fiber-Optic Pyrometers
Abstract
:1. Introduction
2. Theoretical Background and Modeling
2.1. Fiber-Optic Pyrometer Aligned with Target Surface
2.2. Fiber-Optic Pyrometer with a Tilting Angle to Target Surface
2.3. Limits of Integration
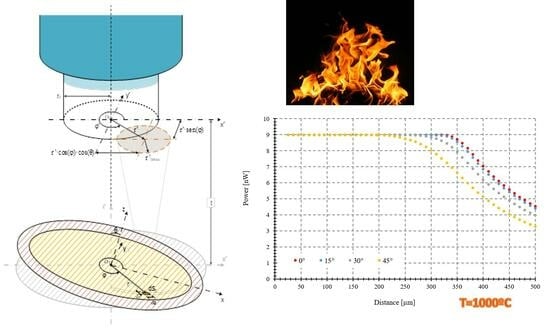
3. Simulations
3.1. Model Validation (Tilting Angle of 0°)
3.2. Tilting Angle Effects on Power Gathered by the Pyrometer
3.3. Maximum Tilting Angle to Avoid Measurement Errors
3.4. Critical Distance as a Function of Tilting Angle
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hartmann, J. High-temperature measurement techniques for the application in photometry, radiometry and thermometry. Phys. Rep. 2009, 469, 205–269. [Google Scholar] [CrossRef]
- Díaz-Álvarez, J.; Tapetado, A.; Vázquez, C.; Miguélez, H. Temperature measurement and numerical prediction in machining inconel 718. Sensors 2017, 17, 1531. [Google Scholar] [CrossRef] [PubMed]
- Möllmann, K.P.; Vollmer, M. IR imaging of microsystems: Special requirements experiments and applications. In Proceedings of the International Conference on Infrared Sensors & Systems, Nurnberg, Germany, 7–9 June 2011. [Google Scholar]
- Mahal, J.; Good, P.; Ambrosetti, G.; Cooper, T.A. Contactless thermal mapping of high-temperature solar receivers via narrow-band near-infrared thermography. Solar Energy 2022, 246, 331–342. [Google Scholar] [CrossRef]
- Kim, M.M.; Giry, A.; Mastiani, M.; Rodrigues, G.O.; Reis, A.; Mandin, P. Microscale thermometry: A review. Microelectron. Eng. 2015, 148, 129–142. [Google Scholar] [CrossRef]
- Öner, B.; Pomeroy, J.W.; Kuball, M. Submicrometer resolution hyperspectral quantum rod thermal imaging of microelectronic devices. ACS Appl. Electron. Mater. 2020, 2, 93–102. [Google Scholar] [CrossRef]
- Wu, J.; Li, J.; Li, J.; Zhou, X.; Weng, J.; Liu, S.; Tao, T.; Ma, H.; Tang, L.; Gao, Z.; et al. A sub-nanosecond pyrometer with broadband spectral channels for temperature measurement of dynamic compression experiments. Measurement 2022, 195, 111147. [Google Scholar] [CrossRef]
- Núñez-Cascajero, A.; Tapetado, A.; Vargas, S.; Vázquez, C. Optical fiber pyrometer designs for temperature measurements depending on object size. Sensors 2021, 21, 646. [Google Scholar] [CrossRef]
- Tapetado, A.; Diaz-Alvarez, J.; Miguelez, M.H.; Vázquez, C. Fiber-Optic Pyrometer for Very Localized Temperature Measurements in a Turning Process. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 278–283. [Google Scholar] [CrossRef]
- Nuñez Cascajero, A.; Tapetado, A.; Vázquez, C. High Spatial Resolution Optical Fiber Two Color Pyrometer with Fast Response. IEEE Sens. J. 2021, 21, 2942–2950. [Google Scholar] [CrossRef]
- Tapetado, A.; Diaz-Alvarez, J.; Miguelez, M.H.; Vázquez, C. Two-color pyrometer for process temperature measurement during machining. J. Light. Technol. 2016, 34, 1380–1386. [Google Scholar] [CrossRef]
- Vázquez, C.; Pérez-Prieto, S.; López-Cardona, J.D.; Tapetado, A.; Blanco, E.; Moreno-López, J.; Montero, D.S.; Lallana, P.C. Fiber-optic pyrometer with optically powered switch for temperature measurements. Sensors 2018, 18, 483. [Google Scholar] [CrossRef] [PubMed]
- Davoodi, B.; Hosseinzadeh, H. A new method for heat measurement during high speed machining. Measurement 2012, 45, 2135–2140. [Google Scholar] [CrossRef]
- Aretusini, S.; Núñez-Cascajero, A.; Spagnuolo, E.; Tapetado, A.; Vázquez, C.; di Toro, G. Fast and Localized Temperature Measurements During Simulated Earthquakes in Carbonate Rocks. Geophys. Res. Lett. 2021, 48, e2020GL091856. [Google Scholar] [CrossRef] [PubMed]
- Mekhrengin, M.V.; Meshkovskii, I.K.; Tashkinov, V.A.; Guryev, V.I.; Sukhinets, A.V.; Smirnov, D.S. Multispectral pyrometer for high temperature measurements inside combustion chamber of gas turbine engines. Measurement 2019, 139, 355–360. [Google Scholar] [CrossRef]
- Koyano, T.; Goto, E.; Hosokawa, A.; Furumoto, T.; Hashimoto, Y.; Yamaguchi, M.; Abe, S. Measurement of Wire Electrode Temperature in Wire Electrical Discharge Machining by Two-color Pyrometer with Optical Fiber. Procedia CIRP 2022, 113, 273–277. [Google Scholar] [CrossRef]
- Shmygalev, A.S.; Suchkova, D.S.; Zhilyakov, A.V.; Korsakov, A.S.; Zhilkin, B.P. Fiber pyrometer for the control of Baker’s cyst laser obliteration. In Proceedings of the International Conference Laser Optics 2018, Saint Petersburg, Russia, 4–8 June 2018. [Google Scholar]
- Wang, B.; Niu, Y.; Qin, X.; Yin, Y.; Ding, M. Review of high temperature measurement technology based on sapphire optical fiber. Measurement 2021, 184, 109868. [Google Scholar] [CrossRef]
- Zur, A.; Katzir, A. Fibers for low-temperature radiometric measurements. Appl. Opt. 1987, 26, 1201–1206. [Google Scholar] [CrossRef]
- Ning, D.; Shoshin, Y.; Van Oijen, J.A.; Finotello, G.; Goey, L.P.H. Critical temperature for nanoparticle cloud formation during combustion of single micron-sized iron particle. Combust. Flame 2022, 244, 112296. [Google Scholar] [CrossRef]
- May, R.G.; Moneyhun, S.; Saleh, W.; Sudeora, S.; Claus, R.O.; Buoncristiani, A.M. IR Optical Fiber-Based Noncontact Pyrometer for Drop Tube Instrumentation. Infrared Fiber Opt. 1989, 1048, 175–182. [Google Scholar]
- Bouvry, B.; Cheymol, G.; Gallou, C.; Maskrot, H.; Destouches, C.; Ferry, L.; Gonnier, C. Theoretical and Experimental Analyses of the Impact of High-Temperature Surroundings on the Temperature Estimated by an Optical Pyrometry Technique. IEEE Trans. Nucl. Sci. 2018, 65, 2593–2600. [Google Scholar] [CrossRef]
- Safarloo, S.; Tapetado, A.; Vázquez, C. Experimental Validation of High Spatial Resolution of Two-Color Optical Fiber Pyrometer. Sensors 2023, 23, 4320. [Google Scholar] [CrossRef] [PubMed]
- Tapetado, A. Fiber Optic Sensors and Self-Reference Techniques for Temperature Measurements in Different Industrial Sectors. Ph.D. Thesis, Carlos III University of Madrid, Madrid, Spain, 2015. [Google Scholar]
- Ueda, T.; Sato, M.; Sugita, T.; Nakayama, K. Thermal Behaviour of Cutting Grain in Grinding. CIRP Ann. Manuf. Technol. 1995, 44, 325–328. [Google Scholar] [CrossRef]












| Variable | Meaning | Variable | Meaning |
|---|---|---|---|
| dST | Differential element of target surface | rT | Radius of the target |
| rF | Optical fiber (OF) core radius | β | Angle between the normal to dST and the vector from dST to each solid angle differential in the intersection of the circles with radii rF and rβmax or r’βmax |
| rβmax, r’βmax * | Radius of the circle defined by the cone projection of the light, due to OF NA, from dST on the fiber end plane | dF | Differential element of area of circle with radius rβmax or r’βmax |
| t, t’ * | Minimum distance from dST to fiber end plane on each model | u | Radial coordinate of each differential element of area dF |
| r | Radial coordinate of dST on the plane of the target | δ | Azimuthal coordinate of each differential element of area dF |
| r’ | Distance between the centers of the circles with radii rF and rβmax or r’βmax | θ | Angle between the fiber axis and the normal to the emitting target surface |
| ϕ, φ | Azimuthal coordinate of dST on the plane of the target on each model | rNA | Radius of the circle defined by the optical fiber field of view due numerical aperture, on the target plane |
| φ’ | Angle between r’ and x’ axis on the fiber end plane | βmax | Maximum acceptance angle of OF |
| 0 < r’ < rF − r’βmax | rF − r’βmax < r’ < rF | rF < r’ < rF + r’βmax | ||||
|---|---|---|---|---|---|---|
| r’βmax < rF | Int. Sit. | Circum. | Circum. | Arcs | Arcs | |
| umin | 0 | 0 | rF − r’ | r’ − rF | ||
| umax | r’βmax | rF - r’ | r’βmax | r’βmax | ||
| rF < r’βmax < 2rF | Int. Sit. | Circum. | Arcs | Circum. | Arcs | Arcs |
| umin | 0 | rF − r’ | 0 | rF − r’ | r’ − rF | |
| umax | rF − r’ | rF + r’ | rF − r’ | r’βmax | r’βmax | |
| 2rF < r’βmax | Int. Sit. | Circum. | Arcs | Arcs | Arcs | |
| umin | 0 | rF − r’ | r’ − rF | r’ − rF | ||
| umax | rF − r’ | rF + r’ | r’ + rF | r’βmax | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vargas, S.; Tapetado, A.; Vázquez, C. Influence of Tilting Angle on Temperature Measurements of Different Object Sizes Using Fiber-Optic Pyrometers. Sensors 2023, 23, 8119. https://doi.org/10.3390/s23198119
Vargas S, Tapetado A, Vázquez C. Influence of Tilting Angle on Temperature Measurements of Different Object Sizes Using Fiber-Optic Pyrometers. Sensors. 2023; 23(19):8119. https://doi.org/10.3390/s23198119
Chicago/Turabian StyleVargas, Salvador, Alberto Tapetado, and Carmen Vázquez. 2023. "Influence of Tilting Angle on Temperature Measurements of Different Object Sizes Using Fiber-Optic Pyrometers" Sensors 23, no. 19: 8119. https://doi.org/10.3390/s23198119
APA StyleVargas, S., Tapetado, A., & Vázquez, C. (2023). Influence of Tilting Angle on Temperature Measurements of Different Object Sizes Using Fiber-Optic Pyrometers. Sensors, 23(19), 8119. https://doi.org/10.3390/s23198119