LS-VCE Applied to Stochastic Modeling of GNSS Observation Noise and Process Noise
Abstract
:1. Introduction
2. Methods
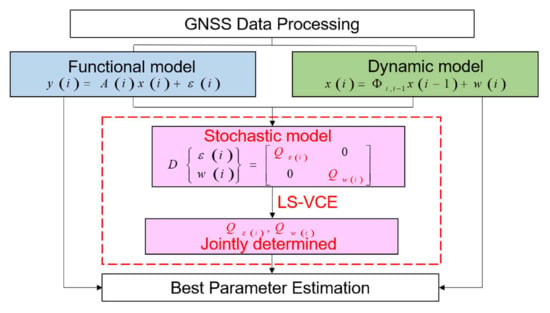
2.1. GNSS Mathematical Models
2.2. Least-Squares Variance Component Estimation
2.3. Stochastic Modeling of GNSS Observation Noise and RCB Process Noise
2.3.1. Functional and Dynamic Models
2.3.2. Formulation of the Stochastic Model
2.3.3. Estimation of Variances for Observation Noise and Process Noise
3. Experiments and Results
3.1. Experiment Setup
3.2. Characteristics of Receiver Biases
3.3. Variances of GNSS Observation Noise and RCB Process Noise
3.4. Validation and Impact of the Stochastic Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; Wiley: Hoboken, NJ, USA, 2015; ISBN 978-1-118-67557-1. [Google Scholar]
- Teunissen, P.J.G.; Kleusberg, A. GPS for Geodesy, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Koch, K.-R. Parameter Estimation and Hypothesis Testing in Linear Models; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Teunissen, P.J.G.; Montenbruck, O. Springer Handbook of Global Navigation Satellite Systems; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Morton, Y.J.; van Diggelen, F.; Spilker, J.J., Jr.; Parkinson, B.W.; Lo, S.; Gao, G. Position, Navigation, and Timing Technologies in the 21st Century: Integrated Satellite Navigation, Sensor Systems, and Civil Applications; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Wübbena, G.; Schmitz, M.; Bagge, A. PPP-RTK: Precise point positioning using state-space representation in RTK networks. In Proceedings of the ION GNSS 2005, The Institute of Navigation, Long Beach, CA, USA, 13–16 September 2005; pp. 2584–2594. [Google Scholar]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Earth Surf. 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P.J.G. Adjustment theory: An introduction; VSSD, Delft University Press: Delft, The Netherlands, 2000. [Google Scholar]
- Amiri-Simkooei, A.R.; Teunissen, P.J.G.; Tiberius, C. Application of Least-Squares Variance Component Estimation to GPS Observables. J. Surv. Eng. 2009, 135, 149–160. [Google Scholar] [CrossRef] [Green Version]
- Bona, P. Precision, Cross Correlation, and Time Correlation of GPS Phase and Code Observations. GPS Solut. 2000, 4, 3–13. [Google Scholar] [CrossRef]
- de Bakker, P.F.; Tiberius, C.C.; van der Marel, H.; van Bree, R.J. Short and zero baseline analysis of GPS L1 C/A, L5Q, GIOVE E1B, and E5aQ signals. GPS Solut. 2012, 16, 53–64. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P. Testing Theory; VSSD, Delft University Press: Delft, The Netherlands, 2006. [Google Scholar]
- Teunissen, P.J.G.; Amiri-Simkooei, A.R. Least-squares variance component estimation. J. Geod. 2007, 82, 65–82. [Google Scholar] [CrossRef] [Green Version]
- Koch, K.R. Maximum likelihood estimate of variance components. J. Geod. 1986, 60, 329–338. [Google Scholar] [CrossRef]
- Kubik, K. The estimation of the weights of measured quantities within the method of least squares. Bull. Géodésique 1970, 95, 21–40. [Google Scholar] [CrossRef]
- Kusche, J. A Monte-Carlo technique for weight estimation in satellite geodesy. J. Geod. 2003, 76, 641–652. [Google Scholar] [CrossRef] [Green Version]
- Rao, C. Estimation of variance and covariance components—MINQUE theory. J. Multivar. Anal. 1971, 1, 257–275. [Google Scholar] [CrossRef] [Green Version]
- Amiri-Simkooei, A. Least-Squares VarianceComponent Estimation: Theory and GPS Applications. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2007. [Google Scholar]
- Amiri-Simkooei, A.; Zangeneh-Nejad, F.; Asgari, J. Least-squares variance component estimation applied to GPS geome-try-based observation model. J. Surv. Eng. 2013, 139, 176–187. [Google Scholar] [CrossRef]
- Li, B.; Shen, Y.; Xu, P. Assessment of stochastic models for GPS measurements with different types of receivers. Sci. Bull. 2008, 53, 3219–3225. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Hou, P.; Liu, T.; Yuan, Y. A single-receiver geometry-free approach to stochastic modeling of multi-frequency GNSS observables. J. Geod. 2020, 94, 1–21. [Google Scholar] [CrossRef]
- Hou, P.; Zhang, B.; Yuan, Y. Combined GPS+BDS instantaneous single- and dual-frequency RTK positioning: Stochastic modelling and performance assessment. J. Spat. Sci. 2019, 66, 3–26. [Google Scholar] [CrossRef]
- Hou, P.; Zhang, B.; Yuan, Y.; Zhang, X.; Zha, J. Stochastic modeling of BDS2/3 observations with application to RTD/RTK positioning. Meas. Sci. Technol. 2019, 30, 095002. [Google Scholar] [CrossRef]
- Li, B. Stochastic modeling of triple-frequency BeiDou signals: Estimation, assessment and impact analysis. J. Geod. 2016, 90, 593–610. [Google Scholar] [CrossRef]
- Hu, H.; Xie, X.; Gao, J.; Jin, S.; Jiang, P. GPS-BDS-Galileo double-differenced stochastic model refinement based on least-squares variance component estimation. J. Navig. 2021, 74, 1381–1396. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J. Low-cost, 4-system, precise GNSS positioning: A GPS, Galileo, BDS and QZSS iono-sphere-weighted RTK analysis. Meas. Sci. Technol. 2017, 28, 125801. [Google Scholar] [CrossRef] [Green Version]
- Zaminpardaz, S.; Teunissen, P.J.G. Analysis of Galileo IOV + FOC signals and E5 RTK performance. GPS Solut. 2017, 21, 1855–1870. [Google Scholar] [CrossRef]
- Mi, X.; Sheng, C.; El-Mowafy, A.; Zhang, B. Characteristics of receiver-related biases between BDS-3 and BDS-2 for five fre-quencies including inter-system biases, differential code biases, and differential phase biases. GPS Solut. 2021, 25, 1–11. [Google Scholar] [CrossRef]
- Zha, J.; Zhang, B.; Yuan, Y.; Zhang, X.; Li, M. Use of modified carrier-to-code leveling to analyze temperature dependence of multi-GNSS receiver DCB and to retrieve ionospheric TEC. GPS Solut. 2019, 23, 1–12. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.G. Characterization of multi-GNSS between-receiver differential code biases using zero and short baselines. Sci. Bull. 2015, 60, 1840–1849. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Yuan, H.; Li, B.; He, X.; Gao, S. Feasibility of easy-to-implement methods to analyze systematic errors of multipath, differential code bias, and inter-system bias for low-cost receivers. GPS Solut. 2021, 25, 1–14. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, C.; Odolinski, R.; Liu, T. Functional model modification of precise point positioning considering the time-varying code biases of a receiver. Satell. Navig. 2021, 2, 1–10. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. A canonical theory for short GPS baselines. J. Geod. 1997, 71, 320–336. [Google Scholar] [CrossRef]
- Teunissen, P.; Khodabandeh, A.; Psychas, D. A generalized Kalman filter with its precision in recursive form when the sto-chastic model is misspecified. J. Geod. 2021, 95, 1–12. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G.; Odijk, D. Combined GPS + BDS for short to long baseline RTK positioning. Meas. Sci. Technol. 2015, 26. [Google Scholar] [CrossRef]
- Eueler, H.-J.; Goad, C.C. On optimal filtering of GPS dual frequency observations without using orbit information. J. Geod. 1991, 65, 130–143. [Google Scholar] [CrossRef]
- Zhang, Z. Code and phase multipath mitigation by using the observation-domain parameterization and its application in five-frequency GNSS ambiguity resolution. GPS Solut. 2021, 25, 1–14. [Google Scholar] [CrossRef]
- Barnes, D. GPS Status and Modernization. Presentation at Munich Satellite Navigation Summit. 2019. Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a550403.pdf (accessed on 22 December 2021).
- Benedicto, J. Directions 2020: Galileo moves ahead. GPS World 2019, 30, 38–47. [Google Scholar]
- CSNO. Development of the BeiDou Navigation Satellite System (Version 4.0). 2019. Available online: http://www.beidou.gov.cn/xt/gfxz/201912/P020191227430565455478.pdf (accessed on 22 December 2021).
- Zrinjski, M.; Barković, Đ.; Matika, K. Development and Modernization of GNSS. Geod. List 2019, 73, 45–65. [Google Scholar]












| Estimable Parameter | Notation and Interpretation |
|---|---|
| Receiver clock | |
| Receiver code bias | |
| Receiver phase bias | |
| Integer ambiguity |
| Baseline | System | RCB (mm) | Code 1 (m) | Code 2 (m) | Phase (mm) |
|---|---|---|---|---|---|
| IGG1–IGG2 | GPS | 0.61 | 0.21 | 0.26 | 2.01 |
| Galileo | 0.69 | 0.17 | 0.23 | 2.57 | |
| BDS | 0.74 | 0.31 | 0.13 | 1.73 | |
| IGG1–IGG3 | GPS | 0.62 | 0.38 | 0.35 | 2.35 |
| Galileo | 0.70 | 0.21 | 0.26 | 2.89 | |
| BDS | 0.61 | 0.36 | 0.17 | 1.93 | |
| IGG2–IGG3 | GPS | 0.75 | 0.34 | 0.27 | 1.52 |
| Galileo | 0.83 | 0.14 | 0.24 | 2.39 | |
| BDS | 0.81 | 0.31 | 0.12 | 1.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, P.; Zha, J.; Liu, T.; Zhang, B. LS-VCE Applied to Stochastic Modeling of GNSS Observation Noise and Process Noise. Remote Sens. 2022, 14, 258. https://doi.org/10.3390/rs14020258
Hou P, Zha J, Liu T, Zhang B. LS-VCE Applied to Stochastic Modeling of GNSS Observation Noise and Process Noise. Remote Sensing. 2022; 14(2):258. https://doi.org/10.3390/rs14020258
Chicago/Turabian StyleHou, Pengyu, Jiuping Zha, Teng Liu, and Baocheng Zhang. 2022. "LS-VCE Applied to Stochastic Modeling of GNSS Observation Noise and Process Noise" Remote Sensing 14, no. 2: 258. https://doi.org/10.3390/rs14020258
APA StyleHou, P., Zha, J., Liu, T., & Zhang, B. (2022). LS-VCE Applied to Stochastic Modeling of GNSS Observation Noise and Process Noise. Remote Sensing, 14(2), 258. https://doi.org/10.3390/rs14020258