Mapping Topobathymetry in a Shallow Tidal Environment Using Low-Cost Technology
Abstract
:1. Introduction
2. Study Area
3. Material and Methods
3.1. Topography
3.1.1. Data Acquisition
3.1.2. Data Processing
3.1.3. Indirect Georeferencing and Accuracy
3.2. Bathymetry
3.2.1. Data Acquisition
3.2.2. Data Processing and Accuracy
4. Results and Discussion
4.1. SfM Topography: Derivation and Accuracy
4.2. Bathymetry Accuracy
4.3. Final Topobathymetric Model
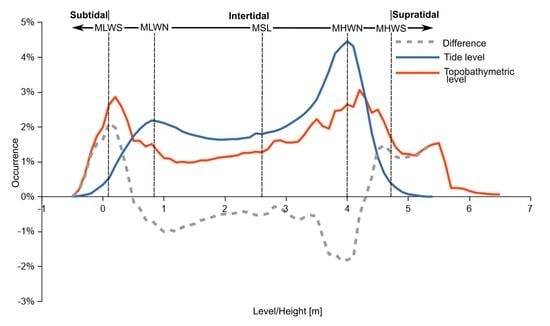
4.4. Cross-Analysis of the Topobathymetric and Tidal Data
4.5. Advantages, Limitations and Applications of Topobathymetry
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cicin-Sain, B.; Knecht, R.W.; Jang, D.; Knecht, R.; Fisk, G.W. Integrated Coastal and Ocean Management: Concepts and Practices; Island Press: Washington, DC, USA, 1998; p. 491. [Google Scholar]
- Alvarez, L.V.; Moreno, H.A.; Segales, A.R.; Pham, T.G.; Pillar-Little, E.A.; Chilson, P.B. Merging Unmanned Aerial Systems (UAS) Imagery and Echo Soundings with an Adaptive Sampling Technique for Bathymetric Surveys. Remote Sens. 2018, 10, 1362. [Google Scholar] [CrossRef] [Green Version]
- Bergsma, E.W.J.; Conley, D.C.; Davidson, M.A.; O’Hare, T.J. Video-based nearshore bathymetry estimation in macro-tidal environments. Mar. Geol. 2016, 374, 31–41. [Google Scholar] [CrossRef] [Green Version]
- Jagalingam, P.; Akshaya, B.J.; Hegde, A.V. Bathymetry mapping using Landsat 8 satellite imagery. Procedia Eng. 2015, 116, 560–566. [Google Scholar] [CrossRef] [Green Version]
- Genchi, S.A.; Vitale, A.J.; Perillo, G.M.E.; Delrieux, C.A. Structure-from-Motion approach for characterization of bioerosion patterns using UAV imagery. Sensors 2015, 15, 3593–3609. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kääb, A.; Girod, L.; Berthling, I. Surface kinematics of periglacial sorted circles using structure-from-motion technology. Cryosphere 2014, 8, 1041–1056. [Google Scholar] [CrossRef] [Green Version]
- Mancini, F.; Dubbini, M.; Gattelli, M.; Stecchi, F.; Fabbri, S.; Gabbianelli, G. Using Unmanned Aerial Vehicles (UAV) for High-Resolution Reconstruction of Topography: The Structure from Motion Approach on coastal environments. Remote Sens. 2013, 5, 6880–6898. [Google Scholar] [CrossRef] [Green Version]
- Jaud, M.; Grasso, F.; Le Dantec, N.; Verney, R.; Delacourt, C.; Ammann, J.; Deloffre, J.; Grandjean, P. Potential of UAVs for Monitoring Mudflat Morphodynamics (Application to the Seine Estuary, France). ISPRS Int. J. Geo-Inform. 2016, 5, 50. [Google Scholar] [CrossRef] [Green Version]
- Long, N.; Millescamps, B.; Guillot, B.; Pouget, F.; Bertin, X. Monitoring the Topography of a Dynamic Tidal Inlet Using UAV Imagery. Remote Sens. 2016, 8, 387. [Google Scholar] [CrossRef] [Green Version]
- Esposito, G.; Salvini, R.; Matano, F.; Sacchi, M.; Danzi, M.; Somma, R.; Troise, C. Multitemporal monitoring of a coastal landslide through SfM-derived point cloud comparison. Photogramm. Rec. 2017, 32, 459–479. [Google Scholar] [CrossRef] [Green Version]
- Pagán, J.I.; Bañón, L.; López, I.; Bañón, C.; Aragonés, L. Monitoring the dune-beach system of Guardamar del Segura (Spain) using UAV, SfM and GIS techniques. Sci. Total Environ. 2019, 687, 1034–1045. [Google Scholar] [CrossRef]
- Guisado-Pintado, E.; Jackson, D.W.T.; Rogers, D. 3D mapping efficacy of a drone and terrestrial laser scanner over a temperate beach-dune zone. Geomorphology 2019, 328, 157–172. [Google Scholar] [CrossRef]
- Tonkin, T.N.; Midgley, N.G.; Graham, D.J.; Labadz, J.C. The potential of small unmanned aircraft systems and structure-from-motion for topographic surveys: A test of emerging integrated approaches at Cwm Idwal, North Wales. Geomorphology 2014, 226, 35–43. [Google Scholar] [CrossRef] [Green Version]
- Gesch, D.B.; Brock, J.C.; Parrish, C.E.; Rogers, J.N.; Wright, C.W. Introduction: Special Issue on Advances in Topobathymetric Mapping, Models. J. Coast. Res. 2016, 76, 1–3. [Google Scholar] [CrossRef]
- Collin, A.; Hench, J.L.; Pastol, Y.; Planes, S.; Thiault, L.; Schmitt, R.J.; Holbrook, S.J.; Davies, N.; Troyer, M. High resolution topobathymetry using a Pleiades-1 triplet: Moorea Island in 3D. Remote Sens. Environ. 2018, 208, 109–119. [Google Scholar] [CrossRef]
- Gesch, D.; Wilson, R. Development of a seamless multisource topographic/bathymetric elevation model of Tampa Bay. Mar. Technol. Soc. J. 2001, 35, 58–64. [Google Scholar] [CrossRef] [Green Version]
- Quadros, N.D.; Collier, P.A.; Fraser, C.S. Integration of Bathymetric and Topographic LiDAR: A Preliminary Investigation. ISPRS Arch. 2008, 37, 1299–1304. [Google Scholar]
- Eakins, B.W.; Grothe, P.R. Challenges in building coastal digital elevation models. J. Coast. Res. 2014, 30, 942–953. [Google Scholar] [CrossRef] [Green Version]
- Danielson, J.J.; Poppenga, S.K.; Brock, J.C.; Evans, G.A.; Tyler, D.J.; Gesch, D.B.; Thatcher, C.A.; Barras, J.A. Topobathymetric elevation model development using a new methodology: Coastal national elevation database. J. Coast. Res. 2016, 76, 75–89. [Google Scholar] [CrossRef] [Green Version]
- Andersen, M.S.; Gergely, Á.; Al-Hamdani, Z.; Steinbacher, F.; Larsen, L.R.; Ernstsen, V.B.J.H.; Sciences, E.S. Processing and performance of topobathymetric lidar data for geomorphometric and morphological classification in a high-energy tidal environment. Hydrol. Earth Syst. Sci. 2017, 21, 43–63. [Google Scholar] [CrossRef] [Green Version]
- Ojeda Zújar, J.; Álvarez Francoso, J.I.; Fraile Jurado, P.; Márquez Pérez, J.; Sánchez Rodríguez, E. Gestión e integración de datos altimétricos y batimétricos en la costa andaluza: El uso del “model builder”. In Tecnologías de la Información Geográfica: La Información Geográfica al Servicio de los Ciudadanos; Ojeda, J., Pita, M.F., Vallejo, I., Eds.; Secretariado de Publicaciones de la Universidad de Sevilla: Sevilla, Spain, 2010; pp. 956–970. [Google Scholar]
- Feyen, J.; Hess, K.; Spargo, E.; Wong, A.; White, S.; Sellars, J.; Gill, S. Development of a continuous bathymetric/topographic unstructured coastal flooding model to study sea level rise in North Carolina. In Proceedings of the International Conference on Estuarine and Coastal Modeling 2005, Charleston, SC, USA, 31 October–2 November 2005; Spaulding, M.L., Ed.; ASCE: Reston, VA, USA, 2006; pp. 338–356. [Google Scholar]
- Foxgrover, A.C.; Finlayson, D.P.; Jaffe, B.E. Bathymetry and Digital Elevation Model of Coyote Creek and Alviso Slough, South San Francisco Bay; U.S. Geological Survey: Reston, CA, USA, 2011; p. 23. [CrossRef]
- Medeiros, S.C.; Ali, T.A.; Hagen, S.C.; Raiford, J.P. Development of a seamless topographic/bathymetric digital terrain model for tampa bay, Florida. Photogramm. Eng. Remote Sens. 2011, 77, 1249–1256. [Google Scholar] [CrossRef]
- Nayegandhi, A.; Brock, J.C.; Wright, C.W. Small-footprint, waveform-resolving lidar estimation of submerged and sub-canopy topography in coastal environments. Int. J. Remote Sens. 2009, 30, 861–878. [Google Scholar] [CrossRef]
- Perillo, G.M.E.; Piccolo, M.C.; Parodi, E.; Freije, R.H. The Bahia Blanca Estuary, Argentina. In Coastal Marine Ecosystems of Latin America. Ecological Studies (Analysis and Synthesis); Seeliger, U., Kjerfve, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 144, pp. 205–217. [Google Scholar] [CrossRef]
- Popovich, C.A.; Marcovecchio, J.E. Spatial and temporal variability of phytoplankton and environmental factors in a temperate estuary of South America (Atlantic coast, Argentina). Cont. Shelf Res. 2008, 28, 236–244. [Google Scholar] [CrossRef]
- Perillo, G.M.E.; Piccolo, M.C. Geomorphologic and physical characteristics of the Bahía Blanca Estuary. Argentina. In Estuaries of South America: Their Geomorphology and Dynamics; Environmental Science Series; Perillo, G.M.E., Piccolo, M.C., Pino Quivira, M., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 195–216. [Google Scholar]
- Perillo, G.M.E.; Iribarne, O.O. Processes of tidal channels develop in salt and freshwater marshes. Earth Surf. Process. Landf. 2003, 28, 1473–1482. [Google Scholar] [CrossRef]
- Escapa, C.M.; Minkoff, D.R.; Perillo, G.M.E.; Iribarne, O.O. Direct and indirect effects of burrowing crab activities on erosion of Southwest Atlantic Sarcocornia-dominated marshes. Limnol. Oceanogr. 2007, 52, 2340–2349. [Google Scholar] [CrossRef]
- Jaud, M.; Passot, S.; Le Bivic, R.; Delacourt, C.; Grandjean, P.; Le Dantec, N. Assessing the accuracy of high resolution digital surface models computed by PhotoScan® and MicMac® in sub-optimal survey conditions. Remote Sens. 2016, 8, 465. [Google Scholar] [CrossRef] [Green Version]
- James, M.R.; Robson, S.; d’Oleire-Oltmanns, S.; Niethammer, U. Optimising UAV topographic surveys processed with structure-from-motion: Ground control quality, quantity and bundle adjustment. Geomorphology 2017, 280, 51–66. [Google Scholar] [CrossRef] [Green Version]
- Chadwick Jr, W.W.; Scheirer, D.S.; Embley, R.W.; Johnson, H.P. High-resolution bathymetric surveys using scanning sonars: Lava flow morphology, hydrothermal vents, and geologic structure at recent eruption sites on the Juan de Fuca Ridge. J. Geophys. Res. Solid Earth. 2001, 106, 16075–16099. [Google Scholar] [CrossRef]
- Krüger, R.; Karrasch, P.; Bernard, L. Evaluating Spatial Data Acquisition and Interpolation Strategies for River Bathymetries. In Geospatial Technologies for All. AGILE 2018. Lecture Notes in Geoinformation and Cartography; Mansourian, A., Pilesjö, P., Harrie, L., van Lammeren, R., Eds.; Springer: Cham, Germany, 2018; pp. 3–25. [Google Scholar]
- Gosciewski, D. Selection of interpolation parameters depending on the location of measurement points. GISci. Remote Sens. 2013, 50, 515–526. [Google Scholar] [CrossRef]
- Curtarelli, M.; Leão, J.; Ogashawara, I.; Lorenzzetti, J.; Stech, J. Assessment of Spatial Interpolation Methods to Map the Bathymetry of an Amazonian Hydroelectric Reservoir to Aid in Decision Making for Water Management. ISPRS Int. J. Geo-Inform. 2015, 4, 220–235. [Google Scholar] [CrossRef]
- Wu, C.Y.; Mossa, J.; Mao, L.; Almulla, M. Comparison of different spatial interpolation methods for historical hydrographic data of the lowermost Mississippi River. Ann. GIS. 2019, 25, 133–151. [Google Scholar] [CrossRef]
- Perillo, G.M.E. Tidal Courses: Classification, Origin and Functionality. In Coastal Wetlands: An Integrated Ecosystem Approach; Perillo, G.M.E., Wolanski, E., Cahoon, D.R., Brinson, M.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2009; pp. 185–209. [Google Scholar]
- Pugh, D.T. Natural Tides, Surges and Mean Sea-Level; John Wiley & Sons: New York, NY, USA, 1996; p. 486. [Google Scholar]
- Liu, X.; Xia, J.; Wright, G.; Arnold, L. A state of the art review on High Water Mark (HWM) determination. Ocean Coast. Manag. 2014, 102, 178–190. [Google Scholar] [CrossRef]
- Daidu, F.; Yuan, W.; Min, L. Classifications, sedimentary features and facies associations of tidal flats. J. Palaeogeogr. 2013, 2, 66–80. [Google Scholar] [CrossRef]
- Perillo, G.M.E.; Piccolo, M.C. Tidal Response in the Bahia Blanca Estuary, Argentina. J. Coast. Res. 1991, 7, 437–449. [Google Scholar]
- Allen, J.R.L. Sedimentary structures: Sorby and the last decade. J. Geol. Soc. Lond. 1993, 150, 417–425. [Google Scholar] [CrossRef]
- Freire, P.; Ferreira, O.; Taborda, R.; Oliveira, F.S.B.F.; Carrasco, A.R.; Silva, A.; Vargas, C.; Capitão, R.; Fortes, C.J.; Coli, A.B.; et al. Morphodynamics of Fetch-limited Beaches in Contrasting Environments. J. Coast. Res. 2009, SI 56, 183–187. [Google Scholar]
- Specht, M.; Specht, C.; Lasota, H.; Cywiński, P. Assessment of the steering precision of a hydrographic Unmanned Surface Vessel (USV) along sounding profiles using a low-cost Multi-Global Navigation Satellite System (GNSS) receiver supported autopilot. Sensors 2019, 19, 3939. [Google Scholar] [CrossRef] [Green Version]
- Demetillo, A.T.; Taboada, E.B. Real-time water quality monitoring for small aquatic area using unmanned surface vehicle. Eng. Technol. Appl. Sci. Res. 2019, 9, 3959–3964. [Google Scholar]










| USV Specification | Description |
|---|---|
| Technical Specifications | |
| Cruising speed | 1.5 m s−1 |
| Vehicle weight | ≈12 kg (depending on battery configuration) |
| Payload weight | 4 kg |
| Maximum payload weight | 7 kg |
| Storage capacity | 5 L |
| Dimension | 1 × 0.45 × 0.27 m |
| Standard operation time | 6 h |
| Standard battery bank | 4S - 32,000 mA (2 batteries, 4S - 16,000 mA) |
| Extended battery bank | 4S - 64,000 mA (4 batteries, 4S - 16,000 mA) |
| Autopilot | Ardupilot 2.5 (stable-2.5.1/apm2) |
| Radio telemetry modem | RDF900, 900Mhz, 1W |
| Sonar option 1 | Garmin echo™ 100 (modified to capture the sonar signal; depth resolution: 0.1% FS) |
| Sonar option 2 | Bluerobotics - Ping Sonar |
| Working conditions | |
| Air temperature range | −10 to 50 Cº |
| Wind speed tolerance | Up to 14 m s−1 (calm waters) |
| Wave height tolerance | Up to 1 m |
| Minimum turning radius | 2.5 m |
| Water flow tolerance (opposite flow direction) | Up to 0.5 m s−1 |
| Water level depth | From 0.3 up to 100 m (depending on transducer) |
| GCP/CP | X | Y | Z |
|---|---|---|---|
| GCP1 | 0.239 | 0.206 | −0.094 |
| GCP2 | −0.0208 | 0.126 | 0.102 |
| GCP3 | −0.110 | −0.148 | −0.055 |
| GCP4 | 0.0139 | −0.184 | 0.005 |
| GCP5 | 0.0556 | −0.003 | 0.074 |
| GCP6 | 0.1095 | 0.0312 | −0.100 |
| GCP7 | −0.266 | −0.008 | 0.018 |
| Mean | 0.003 | 0.003 | −0.007 |
| SD | 0.161 | 0.139 | 0.079 |
| MAV | 0.116 | 0.101 | 0.064 |
| RMSE | 0.149 | 0.129 | 0.074 |
| CP1 | −0.130 | −0.036 | 0.106 |
| CP2 | −0.075 | 0.067 | 0.027 |
| CP3 | 0.126 | 0.015 | 0.096 |
| CP4 | −0.063 | −0.080 | −0.113 |
| Mean | −0.036 | −0.009 | 0.029 |
| SD | 0.112 | 0.064 | 0.101 |
| MAV | 0.099 | 0.049 | 0.086 |
| RMSE | 0.103 | 0.056 | 0.092 |
| Interp. Method | Error Analysis | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | P | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|
| IDW25 | RMSE | 0.092 | 0.258 | 0.168 | 0.114 | 0.139 | 0.271 | 0.167 | 0.174 | 0.224 | 0.179 |
| MAE | −0.058 | 0.251 | 0.059 | −0.055 | −0.100 | 0.216 | 0.138 | 0.002 | 0.050 | 0.056 | |
| R2 | 0.900 | 0.926 | 0.569 | 0.960 | 0.979 | 0.946 | 0.986 | 0.992 | 0.921 | 0.909 | |
| IDW50 | RMSE | 0.099 | 0.238 | 0.195 | 0.099 | 0.164 | 0.258 | 0.158 | 0.153 | 0.213 | 0.175 |
| MAE | −0.068 | 0.211 | 0.087 | −0.048 | −0.119 | 0.202 | 0.129 | 0.043 | 0.046 | 0.054 | |
| R2 | 0.910 | 0.893 | 0.533 | 0.967 | 0.972 | 0.948 | 0.986 | 0.987 | 0.927 | 0.903 | |
| K25 | RMSE | 0.170 | 0.379 | 0.263 | 0.107 | 0.173 | 0.271 | 0.167 | 0.205 | 0.215 | 0.217 |
| MAE | 0.059 | 0.346 | 0.214 | 0.034 | −0.081 | 0.126 | 0.054 | 0.169 | 0.026 | 0.105 | |
| R2 | 0.640 | 0.838 | 0.795 | 0.948 | 0.915 | 0.896 | 0.958 | 0.973 | 0.917 | 0.876 | |
| K50 | RMSE | 0.163 | 0.369 | 0.235 | 0.118 | 0.165 | 0.251 | 0.129 | 0.209 | 0.221 | 0.207 |
| MAE | 0.013 | 0.329 | 0.189 | 0.023 | −0.077 | 0.093 | 0.045 | 0.169 | −0.005 | 0.087 | |
| R2 | 0.595 | 0.800 | 0.826 | 0.942 | 0.919 | 0.906 | 0.976 | 0.971 | 0.912 | 0.872 | |
| NaN25 | RMSE | 0.168 | 0.344 | 0.301 | 0.101 | 0.181 | 0.242 | 0.172 | 0.142 | 0.207 | 0.207 |
| MAE | 0.009 | 0.317 | 0.233 | 0.042 | −0.082 | 0.153 | 0.000 | 0.110 | 0.030 | 0.090 | |
| R2 | 0.680 | 0.902 | 0.714 | 0.945 | 0.916 | 0.937 | 0.952 | 0.985 | 0.923 | 0.884 | |
| NaN50 | RMSE | 0.196 | 0.360 | 0.257 | 0.121 | 0.162 | 0.203 | 0.119 | 0.205 | 0.215 | 0.204 |
| MAE | 0.027 | 0.328 | 0.221 | 0.059 | −0.037 | 0.112 | 0.016 | 0.171 | 0.010 | 0.101 | |
| R2 | 0.562 | 0.868 | 0.855 | 0.957 | 0.910 | 0.953 | 0.978 | 0.980 | 0.916 | 0.886 | |
| MC25 | RMSE | 0.211 | 0.396 | 0.296 | 0.118 | 0.206 | 0.278 | 0.186 | 0.329 | 0.237 | 0.251 |
| MAE | 0.046 | 0.365 | 0.245 | 0.050 | −0.088 | 0.107 | 0.045 | 0.269 | 0.028 | 0.118 | |
| R2 | 0.551 | 0.867 | 0.809 | 0.939 | 0.872 | 0.878 | 0.951 | 0.945 | 0.898 | 0.857 | |
| MC50 | RMSE | 0.225 | 0.400 | 0.278 | 0.116 | 0.194 | 0.254 | 0.144 | 0.311 | 0.243 | 0.241 |
| MAE | 0.045 | 0.358 | 0.230 | 0.044 | −0.086 | 0.067 | 0.032 | 0.244 | −0.003 | 0.103 | |
| R2 | 0.455 | 0.809 | 0.848 | 0.946 | 0.887 | 0.893 | 0.971 | 0.956 | 0.891 | 0.851 |
| Brand /Model | Price (US$) | Auto- Nomy | Survey Rate (km2 h−1) | Working Conditions | Operational Complexity | Post-pro- Cessing Complexity | Sample Point Density | Inva- Sivity | |
|---|---|---|---|---|---|---|---|---|---|
| UAV | DJI/Phantom 3 standard | 500 to 600 | 15 to 20 min | ≈0.16 (at 70 m height) | WS up to 7 m s−1; no rain; sunlight | Simple | Complex | High | Low |
| USV | EMAC/USV v1.5 | 800 to 1000 | 6 to 8 h | ≈0.06 | WS up to 10 m s−1; WLD from 0.3 m, waves heights less than 0.5 m | Medium | Simple | Medi-um | Low |
| RTKGPS | Swiftnav/Piksi RTK | 1000 | 4 to 24 h | - | Clear sky to party cloudy | Complex | Simple | Low | Mediumto high |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Genchi, S.A.; Vitale, A.J.; Perillo, G.M.E.; Seitz, C.; Delrieux, C.A. Mapping Topobathymetry in a Shallow Tidal Environment Using Low-Cost Technology. Remote Sens. 2020, 12, 1394. https://doi.org/10.3390/rs12091394
Genchi SA, Vitale AJ, Perillo GME, Seitz C, Delrieux CA. Mapping Topobathymetry in a Shallow Tidal Environment Using Low-Cost Technology. Remote Sensing. 2020; 12(9):1394. https://doi.org/10.3390/rs12091394
Chicago/Turabian StyleGenchi, Sibila A., Alejandro J. Vitale, Gerardo M. E. Perillo, Carina Seitz, and Claudio A. Delrieux. 2020. "Mapping Topobathymetry in a Shallow Tidal Environment Using Low-Cost Technology" Remote Sensing 12, no. 9: 1394. https://doi.org/10.3390/rs12091394
APA StyleGenchi, S. A., Vitale, A. J., Perillo, G. M. E., Seitz, C., & Delrieux, C. A. (2020). Mapping Topobathymetry in a Shallow Tidal Environment Using Low-Cost Technology. Remote Sensing, 12(9), 1394. https://doi.org/10.3390/rs12091394