A New Approach of the Global Navigation Satellite System Tomography for Any Size of GNSS Network
Abstract
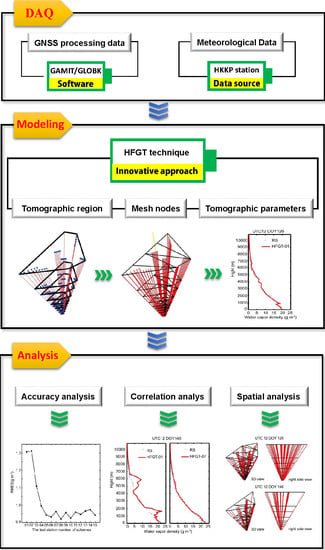
:1. Introduction
2. Methods
2.1. General GNSS Tomography
2.1.1. Observations of GNSS Tomography
2.1.2. GNSS Tomographic Model
2.2. High Flexibility GNSS Tomographic Model
2.2.1. Determination of a Tomographic Region
2.2.2. Determination of Node Density and Position
2.2.3. Estimation of GNSS Tomographic Parameters
3. Results
3.1. GNSS Tomographic Schemes
3.2. Validation of the HFGT
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhao, Q.; Yao, Y.; Yao, W. Troposphere Water Vapour Tomography: A Horizontal Parameterised Approach. Remote Sens. 2018, 10, 1241. [Google Scholar] [CrossRef] [Green Version]
- Flores, A.; Ruffini, G.; Rius, A. 4D tropospheric tomography using GPS slant wet delays. Ann. Geophys. 2000, 18, 223–234. [Google Scholar] [CrossRef]
- Hirahara, K. Local GPS tropospheric tomography. Earth Planets Sp. 2000, 52, 935–939. [Google Scholar] [CrossRef] [Green Version]
- Xia, P.; Cai, C.; Liu, Z. GNSS troposphere tomography based on two-step reconstructions using GPS observations and COSMIC profiles. Ann. Geophys. 2013, 31, 1805–1815. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Liu, Z. Voxel-optimized regional water vapor tomography and comparison with radiosonde and numerical weather model. J. Geod. 2014, 88, 691–703. [Google Scholar] [CrossRef]
- Jiang, P.; Ye, S.R.; Liu, Y.Y.; Zhang, J.J.; Xia, P.F. Near real-time water vapor tomography using ground-based GPS and meteorological data: Long-term experiment in Hong Kong. Ann. Geophys. 2014, 32, 911–923. [Google Scholar] [CrossRef] [Green Version]
- Rohm, W.; Zhang, K.; Bosy, J. Limited constraint, robust Kalman filtering for GNSS troposphere tomography. Atmos. Meas. Tech. 2014, 7, 1475–1486. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.B.; Zhao, Q.Z.; Zhang, B. A method to improve the utilization of GNSS observation for water vapor tomography. Ann. Geophys. 2016, 34, 143–152. [Google Scholar] [CrossRef] [Green Version]
- Ye, S.; Xia, P.; Cai, C. Optimization of GPS water vapor tomography technique with radiosonde and COSMIC historical data. Ann. Geophys. 2016, 34, 789–799. [Google Scholar] [CrossRef] [Green Version]
- Ding, N.; Zhang, S.; Wu, S.; Wang, X.; Kealy, A.; Zhang, K. A new approach for GNSS tomography from a few GNSS stations. Atmos. Meas. Tech. 2018, 11, 3511–3522. [Google Scholar] [CrossRef] [Green Version]
- Seko, H.; Shimada, S.; Nakamura, H.; Kato, T. Three-dimensional distribution of water vapor estimated from tropospheric delay of GPS data in a mesoscale precipitation system of the Baiu front. Earth Planets Sp. 2000, 52, 927–933. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, S.M. Investigations into the Estimation of Tropospheric Delay and Wet Refractivity Using GPS Measurements; Department of Geomatics Engineering, University of Calgary: Calgary, AB, Canada, 2003. [Google Scholar]
- Gradinarsky, L.P.; Jarlemark, P. Ground-Based GPS Tomography of Water Vapor: Analysis of Simulated and Real Data. J. Meteorol. Soc. Jpn. 2004, 82, 551–560. [Google Scholar] [CrossRef] [Green Version]
- Troller, M.R. GPS Based Determination of the Integrated and Spatially Distributed Water Vapor in the Troposphere. Ph.D. Thesis, Eidgenössische Technische Hochschule Zürich, Zürich, Switzerland, 2004. [Google Scholar]
- Hoyle, V.A. Data Assimilation for 4-D Wet Refractivity Modelling in a Regional GPS Network; University of Calgary: Calgary, AB, Canada, 2005. [Google Scholar]
- Bender, M.; Dick, G.; Wickert, J.; Ramatschi, M.; Ge, M.; Gendt, G.; Rothacher, M.; Raabe, A.; Tetzlaff, G. Estimates of the information provided by GPS slant data observed in Germany regarding tomographic applications. J. Geophys. Res. 2009, 114, D06303. [Google Scholar] [CrossRef] [Green Version]
- Donat Perler Water Vapor Tomography Using Global Navigation Satellite Systems; Eidgenössische Technische Hochschule Zürich: Zürich, Switzerland, 2011.
- Shangguan, M.; Bender, M.; Ramatschi, M.; Dick, G.; Wickert, J.; Raabe, A.; Galas, R. GPS tomography: Validation of reconstructed 3-D humidity fields with radiosonde profiles. Ann. Geophys. 2013, 31, 1491–1505. [Google Scholar] [CrossRef]
- Ding, N.; Zhang, S.B.; Wu, S.Q.; Wang, X.M.; Zhang, K.F. Adaptive Node Parameterization for Dynamic Determination of Boundaries and Nodes of GNSS Tomographic Models. J. Geophys. Res. Atmos. 2018, 123, 1990–2003. [Google Scholar] [CrossRef]
- Askne, J.; Nordius, H. Estimation of tropospheric delay for microwaves from surface weather data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; Fan, S.; Cheng, Y. Water vapor-weighted mean temperature and its impact on the determination of precipitable water vapor and its linear trend. J. Geophys. Res. Atmos. 2016, 121, 833–852. [Google Scholar] [CrossRef]
- Shoji, Y.; Nakamura, H.; Iwabuchi, T.; Aonashi, K.; Seko, H.; Mishima, K.; Itagaki, A.; Ichikawa, R.; Ohtani, R. Tsukuba GPS Dense Net Campaign Observation: Improvement in GPS Analysis of Slant Path Delay by Stacking One-way Postfit Phase Residuals. J. Meteorol. Soc. Jpn. 2004, 82, 301–314. [Google Scholar] [CrossRef] [Green Version]
- Kačmařík, M.; Douša, J.; Dick, G.; Zus, F.; Brenot, H.; Möller, G.; Pottiaux, E.; Kapłon, J.; Hordyniec, P.; Václavovic, P.; et al. Inter-technique validation of tropospheric slant total delays. Atmos. Meas. Tech. 2017, 10, 2183–2208. [Google Scholar] [CrossRef] [Green Version]
- Graham, R.L. An efficient algorith for determining the convex hull of a finite planar set. Inf. Process. Lett. 1972, 1, 132–133. [Google Scholar] [CrossRef]
- Ding, N.; Zhang, S.; Zhang, Q. New parameterized model for GPS water vapor tomography. Ann. Geophys. 2017, 35, 311–323. [Google Scholar] [CrossRef] [Green Version]













| Statistics | RMSE | Bias | Standard Deviation | Correlation Coefficient | IQR | Outlier | |
|---|---|---|---|---|---|---|---|
| Scheme | |||||||
| HFGT-01 | 1.305 | −0.294 | 5.998 | 0.975 | 0.990 | 171 | |
| HFGT-02 | 1.311 | 0.202 | 5.455 | 0.989 | 1.055 | 147 | |
| HFGT-03 | 1.108 | 0.126 | 5.790 | 0.984 | 0.982 | 127 | |
| HFGT-04 | 0.994 | −0.086 | 5.886 | 0.988 | 0.952 | 102 | |
| HFGT-05 | 0.943 | 0.059 | 6.093 | 0.988 | 0.860 | 112 | |
| HFGT-06 | 0.931 | −0.112 | 6.073 | 0.991 | 0.880 | 90 | |
| HFGT-07 | 0.962 | −0.126 | 6.074 | 0.991 | 0.819 | 130 | |
| HFGT-08 | 0.919 | −0.112 | 6.061 | 0.992 | 0.841 | 110 | |
| HFGT-09 | 0.956 | −0.119 | 6.043 | 0.991 | 0.856 | 119 | |
| HFGT-10 | 0.925 | −0.133 | 6.088 | 0.990 | 0.848 | 113 | |
| HFGT-11 | 0.959 | −0.142 | 6.042 | 0.991 | 0.844 | 124 | |
| HFGT-12 | 0.946 | −0.132 | 6.031 | 0.991 | 0.868 | 109 | |
| HFGT-13 | 0.965 | −0.165 | 6.068 | 0.991 | 0.864 | 110 | |
| HFGT-14 | 0.973 | −0.170 | 6.103 | 0.987 | 0.870 | 119 | |
| HFGT-15 | 0.942 | −0.162 | 6.051 | 0.990 | 0.844 | 116 | |
| Schemes | Top Region (km²) | Diffusion Coefficient | Mean Altitudinal Angle (°) | Number of Signals |
|---|---|---|---|---|
| HFGT-01 | 908 | 502 | 55 | 39 |
| HFGT-02 | 1199 | 57 | 56 | 61 |
| HFGT-03 | 1239 | 28 | 57 | 97 |
| HFGT-04 | 1437 | 23 | 57 | 129 |
| HFGT-05 | 1608 | 13 | 57 | 162 |
| HFGT-06 | 1939 | 9 | 57 | 202 |
| HFGT-07 | 2185 | 7 | 57 | 244 |
| HFGT-08 | 2591 | 6 | 58 | 276 |
| HFGT-09 | 2733 | 5 | 58 | 316 |
| HFGT-10 | 2847 | 5 | 58 | 354 |
| HFGT-11 | 2920 | 5 | 59 | 391 |
| HFGT-12 | 3118 | 5 | 59 | 425 |
| HFGT-13 | 3206 | 4 | 60 | 459 |
| HFGT-14 | 3303 | 4 | 60 | 493 |
| HFGT-15 | 3359 | 4 | 60 | 528 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Ding, N.; Zhang, Y.; Li, L.; Yang, X.; Zhao, Q. A New Approach of the Global Navigation Satellite System Tomography for Any Size of GNSS Network. Remote Sens. 2020, 12, 617. https://doi.org/10.3390/rs12040617
Wang Y, Ding N, Zhang Y, Li L, Yang X, Zhao Q. A New Approach of the Global Navigation Satellite System Tomography for Any Size of GNSS Network. Remote Sensing. 2020; 12(4):617. https://doi.org/10.3390/rs12040617
Chicago/Turabian StyleWang, Yuchen, Nan Ding, Yu Zhang, Long Li, Xiaoyan Yang, and Qingzhi Zhao. 2020. "A New Approach of the Global Navigation Satellite System Tomography for Any Size of GNSS Network" Remote Sensing 12, no. 4: 617. https://doi.org/10.3390/rs12040617
APA StyleWang, Y., Ding, N., Zhang, Y., Li, L., Yang, X., & Zhao, Q. (2020). A New Approach of the Global Navigation Satellite System Tomography for Any Size of GNSS Network. Remote Sensing, 12(4), 617. https://doi.org/10.3390/rs12040617