Abstract
Microorganisms such as fungi and bacteria cause many human diseases and therefore rapid and accurate identification of these substances is essential for effective treatment and prevention of further infections. In particular, contemporary microbial detection technique is limited by the low detection speed which usually extends over a couple of days. Here we demonstrate that metamaterials operating in the terahertz frequency range shows promising potential for use in fabricating the highly sensitive and selective microbial sensors that are capable of high-speed on-site detection of microorganisms in both ambient and aqueous environments. We were able to detect extremely small amounts of the microorganisms, because their sizes are on the same scale as the micro-gaps of the terahertz metamaterials. The resonant frequency shift of the metamaterials was investigated in terms of the number density and the dielectric constants of the microorganisms, which was successfully interpreted by the change in the effective dielectric constant of a gap area.
Similar content being viewed by others
Introduction
Culture-based detection methods such as polymerase chain reaction (PCR) and fluorescence-based microbial detection systems have been widely used in order to detect and quantify microorganisms1,2,3. However, although the PCR is capable of detecting a wide range of infectious fungi and bacteria, this method is time-consuming and labor-intensive. Conversely, most of fluorescence-based microbial detection systems such as epi-fluorescence microscopy (EFM), flow cytometry (FC) and solid-phase cytometry (SPC) require fluorescent materials for efficient detection of the microorganisms4,5. Optical scattering methods such as light scattering and autofluorescence do not require the dyes; however they suffer from the lack of sensitivity. Therefore, there is an increasing need to develop novel techniques for the effective on-site detection of minute amounts of microbial substances.
Recently, terahertz (THz) spectroscopy has emerged as a promising technique that enables the label-free, non-contact and non-destructive inspection on the chemical and biological substances6,7,8,9,10,11,12,13,14,15. In particular, the recently developed, portable THz spectroscopic tools enable on-site detection and identification of these materials with high signal to noise ratio16,17. THz frequency range detection of microorganisms such as fungi, bacteria and viruses has generated a great deal of interests because of its relevance to food and security inspection18. In many cases, however, the microorganisms are non-responsive in the THz frequency range since they are mostly transparent to THz waves. In addition the size of a typical microorganism is on the order of ~λ/100, resulting in low scattering cross-section.
Metamaterials consist of periodically arranged, sub-wavelength metallic elements and exhibit unique electromagnetic properties such as negative refraction19,20, sub-diffraction limited focusing21,22,23 and cloaking24,25. In addition, the metamaterials have gap structures characterized by strongly localized and enhanced fields, enabling sensitive detection of extremely small amounts of chemical and biological substances26,27,28,29,30,31,32. In particular, metamaterials operating in the THz frequency range have a micro-sized gap33,34,35,36,37,38,39 and can therefore serve as an ideal platform for the sensitive detection of fungi and bacteria, because the size of these microorganisms is compatible with the gap size. Moreover, THz metamaterials are extremely sensitive to the substances near the surface, which is favorable for sensing in aqueous environment since it allows us to use a thin water layer without suffering from the significant loss in the THz wave transmission.
In this work, we performed THz time-domain spectroscopy on metamaterial sensors for the high speed detection of viable and live microorganisms such as molds, yeast cells and bacteria. We measured a frequency shift in the inductive-capacitive resonance following the deposition of microorganisms with very low surface density. In particular, we functionalize the sensors with the antibody specific to bacteria in aqueous environment, enabling the selective detection. The resonance frequency shift in THz metamaterials was studied as a function of the dielectric constants and the density of fungi which is in accordance of the dielectric constant measurement of individual fungi. Our experimental findings are in a good agreement with the results of simulations.
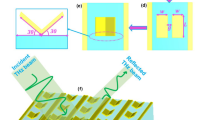
Schematic presentation of the experiments is shown in Fig. 1a. We measured the change in spectra of the THz radiation transmitted through the metamaterials following the deposition of microorganisms. The metamaterials consist of metallic arrays of a square ring with a micro-gap at the center. Here, the resonance of the transmission is determined both by the capacitance (C) of the gap structure and the inductance (L) associated with the shape of the square ring. In other words, the resonance of the transmission dip is expressed by  . The dielectric microorganisms placed in the gap area will cause a change in the effective dielectric constants of the capacitor, resulting in the shift of the resonant frequency in metamaterials.
. The dielectric microorganisms placed in the gap area will cause a change in the effective dielectric constants of the capacitor, resulting in the shift of the resonant frequency in metamaterials.
A representative scanning electron microscopy (SEM) image is shown in Fig. 1b, with the Penicillium chrysogenum (penicillia) deposited on the metamaterials. The fungi samples were grown by a streaking on medium method followed by the incubation at 37°C for 2 days. Metamaterial patterns were prepared by using a conventional photo-lithography method on an undoped Si substrate, followed by the metal deposition in order to define the arrays of split ring resonator patterns with a linewidth of 4 μm and gap sizes of 2–3 μm. THz transmission spectra were obtained by using the THz time-domain spectroscopic techniques with an acquisition time of 5 sec for each spectrum40,41.
We first describe the THz transmission experiments for the low-density microorganisms that were deposited on a plain silicon substrate. Molds and Saccharomyces cerevisiae (yeasts) were deposited on the substrate by rubbing a fungi-coated swab on it. Fig. 2a shows the THz transmission amplitude obtained when the penicillia were deposited on the plain substrate at a density of 0.032/μm2, as shown by the microscope image in the inset of Fig. 2a. No noticeable change in transmission amplitude was found following the deposition of the molds compared to the bare substrate case. Many of the microorganisms such as fungi and bacteria do not have spectral fingerprints in the THz frequency range and thus are basically transparent to the THz waves. Besides, the scattering cross-section of those microbial materials to THz waves is very low, because the typical size of these microorganisms (~μm) is significantly smaller than the wavelength of THz waves. A similar behavior with respect to THz transmission was observed for other microorganisms, such as yeasts and Escherichia coli BL21(DE3) (E. coli), plated at comparable or higher densities (See Supplementary Figure S1).
Metamaterial sensing of penicillia.
(a) THz transmission amplitudes, for transmission through a plain Si substrate, with (red solid line) and without (black dashed line) deposition of penicillia. (inset) A microscopic image of penicillia deposited on the Si substrate. (b) Two microscope images of metamaterials patterns on Si substrate, with the deposition of penicillia a (left) and after fungicide treatments (right). (c) THz transmission amplitudes measured before (gray solid line) and after (red solid line) the deposition. Transmission after the fungicide treatment is shown as blue dashed line.
A representative result on the highly sensitive detection of low-density molds by using the THz metamaterials is demonstrated in the following. Fig. 2b shows two microscopic images of our metamaterial pattern (so-called “electrical split ring resonator”), which is an array of a square ring with a micro-gap at the center33,34. The transmission dip yields 0.837 THz with a full-width at half maximum (FWHM) of 0.15 THz, which corresponds to the inductive-capacitive resonance for the device shown in the image. The left side image in Fig. 2b shows metamaterials with fungi (penicillia) that were deposited at a density of 0.090/μm2 and individual molds that are separated from each other can be clearly seen in this figure. As shown in the right side image, the fungi can be removed completely by using a commercial fungicide (sodium hypochlorite solution). Results for the corresponding THz transmission are shown in Fig. 2c. Unlike the results on the transmission through the plain substrate (Fig. 2a), the resonant frequency exhibited a shift towards the red (red solid line) relative to the resonant frequency obtained for clear metamaterial patterns (gray solid line). The amount of the shift was found to be 9 GHz (6% of the FWHM) for the density of penicillia shown in Fig. 2b. Once the molds were cleaned by using the fungicide, the initial resonant frequency was retrieved (blue dashed line), which verifies the reusability of our metamaterial sensors.
The shift in the resonance frequency can be explained simply by the change of the dielectric environment in the gap area that modifies the capacitance according to C = εA/d, where A is the area, d is the distance and ε is the dielectric constant of the capacitor. It is clear that the increase in the dielectric constant due to the presence of the microorganisms results in the red-shift of the resonant frequency. Similar behaviors were also observed for yeasts and different kinds of molds, such as Neurospora sitophila (neurospora) and Aspergillus niger (niger) (See Supplementary Figure S2). We also performed experiments by using different types of the metamaterial patterns with a gap structure such as single/double split ring resonators and found similar red-shifts following the deposition of fungi; however the electrical split-ring resonator delivers better sensitivity in general (See Supplementary Figure S3).
Our technique can be extended to the highly sensitive detection of bacteria in aqueous environments, which is not accessible by the conventional optical techniques. More importantly, THz metamaterials functionalized with receptors enable the specific sensing of bacteria. A representative result, demonstrating the detection of bacteria (E. coli) in a solution environment, is shown in Fig. 3. The E. coli were deposited from the solution (100 µg/ml) on the Si substrate with metamaterial patterns functionalized with E. coli anti-body42, followed by a rinsing with purified water (Fig. 3a). The patterns were enclosed by a cover glass and the water layer thickness was fixed at 55 μm by using a spacer. This thickness is large enough to cover the small detection volume that is strongly localized at the surface, yet allowing a considerable amount of THz wave transmission. We note that, the E. coli are not as clearly resolved in the solution as they are in the air. Fig. 3b shows the optical transmission spectra in the visible range, obtained for transmission through the quartz substrate coated by the E. coli (density of 0.078/μm2), for both aqueous (red line) and ambient (black line) environments. Transmission through the bare quartz substrate was used as a reference in both cases. The change in the optical transmission reaches only ~1% in water, which is 10-fold smaller as compared to the air. This strongly suggests that the microbial detection techniques based on the scattering of visible light can be limited for some of the microbial systems in the solution phase.
Metamaterial sensing of E. coli in aqueous environment.
(a) A schematic of selective bacteria (E. coli.) detection in solution environment. The Si substrate is coated with antibodies specific to E. coli. (b) Visible transmittance spectra of the quartz substrate coated by E. coli. (density of 0.078 μm2) both in aqueous (red line) and in ambient (black line) conditions. (c) THz transmission before (blue line) and after (red line) the deposition of E. coli. on the functionalized metamaterials in aqueous environments. (inset) A corresponding dark-field microscopic image obtained after the deposition of E. coli. (d) THz transmission before (blue line) and after (red line) the deposition of E. coli. on the sensors without the surface functionalization. (inset) A corresponding dark-field microscopic image after the deposition process.
In contrast, using the THz metamaterials sensors, we can successfully detect the low-density E. coli. Shown in Fig. 3c are the results for the THz transmission obtained with (red line) and without (blue line) the E. coli on the functionalized substrate. The inset of Fig. 3c shows a dark-field microscope image of metamaterials in water with the E. coli (density of 0.019/μm2) adsorbed on the substrate. A clear blue-shift of 23 GHz (yielding ~15% of a FWHM) is observed for the metamaterials with E. coli compared to the case of the clean substrate (blue line). The reason that the deposition of E. coli in aqueous solution causes a blue shift is likely due to the relatively low dielectric constant of E. coli (~1.6 at 1 THz) as compared to that of water (~4.2 at 1 THz)43 (Also see Supplementary Figure S4). Without the surface functionalization, however, we could not observe a noticeable change in the peak position (Fig. 3b). Therefore it is possible to fabricate the biosensors that are specific to the bacteria of interests. Quite obviously, our scheme can be extended to the selective detection of variety of microorganisms such as fungi44 and viruses since the specific binders and their surface functionalization have been widely investigated.
It is evident that the shift in the resonance frequency will strongly depend on the number of fungi and bacteria located in the gap area and on the dielectric constants of the specimens. In Fig. 4, the shift of the resonant frequency is shown as a function of the number density, for different kinds of fungi. The average number of fungi in the gap area was determined by counting them for the entire set of elements (10 × 10) positioned in the spot area of the THz fields (~1 mm2). For example, Fig. 4a shows a series of SEM images of metamaterials with the number of penicillia in the gap area (~3 × 10 μm2) ranging from 0 to 5. Fig. 4b shows the representative data on the resonant frequency shifts, for two different number densities of Nav = 0.59 (corresponding to surface density of 0.020/μm2) and 3.4 (0.113/μm2), respectively from top to bottom for the penicillia. Similar experimental data are shown in Fig. 4c for the yeast cells with Nav = 0.85 (0.028/μm2) and 3.6 (0.120/μm2), respectively. We emphasize that we were able to detect extremely small amounts of fungi, in other words, even in the case when the average number in the gap area was less than unity. A plot of the resonant frequency shift as a function of Nav is shown in Fig. 4d for the penicillia (blue boxes) and yeasts (red circles), respectively. The magnitude of the resonant frequency shift is gradually increasing with Nav for both fungi types. More importantly, it is very clear that the frequency shift is ~3-fold higher in the case of the yeasts. This is a strong indication that the dielectric constant of the yeast is higher than that of the penicillium.
Resonant frequency shift as a function of number density and dielectric constants of fungi.
(a) A series of six SEM images of the metamaterials with the number of penicillia in the gap areas ranging from 0 to 5. (b) THz transmission amplitudes with the penicillia number density of Navg = 0.59 and 3.4, respectively from top to bottom. (c) Same as (b) but with the yeast number density of Navg = 0.85 and 3.6, respectively from top to bottom. (d) A plot of resonant frequency shifts as a function of Navg, for depositions of penicillia (blue boxes) and yeasts (red circles). Solid lines are linear fits to the data.
As mentioned earlier, the resonant frequency shift as a function of Nav and the dielectric constant of the individual fungi (εf) can be analyzed in terms of the changes in the effective dielectric constant of the capacitor. The modified effective dielectric constant ε due to the presence of the fungi in the ambient condition can be expressed as ε = εeff + αN(εf−1), where εeff is the effective dielectric constant without the deposition of fungi, N is the number of microorganisms and α is the coefficient which is associated with the volume fraction of the fungi. Here, εeff in the capacitance (and hence the resonant frequency) is influenced both by the dielectric constants of the substrate and the air41, in which we obtained εeff = 6.4 from simulation results (See Supplementary Figure S5). From the relation  , where f (f0) is the resonant frequency with (without) the deposition of the fungi, the frequency shift Δf = f − f0 leads to
, where f (f0) is the resonant frequency with (without) the deposition of the fungi, the frequency shift Δf = f − f0 leads to  . Here we neglect higher order terms in αN(εf −1)/εeff, since εf/εeff is on the order of or less than unity as will be shown below, whereas α is on the order of 0.01. It is clear from the above equation that, when the density of the microorganisms is low, the frequency shift is linearly dependent on εf − 1 as well as on N.
. Here we neglect higher order terms in αN(εf −1)/εeff, since εf/εeff is on the order of or less than unity as will be shown below, whereas α is on the order of 0.01. It is clear from the above equation that, when the density of the microorganisms is low, the frequency shift is linearly dependent on εf − 1 as well as on N.
To verify the effects of the dielectric constants on the resonant frequency shift, we measured the dielectric constants of the fungi (εf) used in the experiments by preparing thick and dense fungi films. The films were prepared by stacking the large amount of fungi layer by layer on a cellulose membrane. SEM images of the penicillium and yeast films are shown in the insets of Fig. 5a and 5b, respectively. We found from the images that the yeast film consists of very closely packed spheres, whereas that of penicillium is rather loose in general. By measuring both the amplitudes and phases of the transmitted THz pulses, we extracted the complex dielectric constants of the films that consist of the closely packed molds and yeasts. The complex dielectric constants of the thick films (εfilm) are shown in Fig. 5a and 5b for the penicillium and yeast films, respectively.
Dielectric constant measurements of Fungi.
Plots of frequency-dependent, complex dielectric constants of the penicillium (a) and yeast (b) films, extracted from the THz transmission experiments. Films' thickness were 350 and 125 μm, respectively. Shown together are the dielectric constants of the individual penicillium (c) and yeast (d), extracted from (a) and (b) by using a Maxwell-Garnet theory.
The dielectric constants of the fungi can be obtained from those of the films by using the effective medium theory (Maxwell-Garnett model) of (εfilm − 1)/(εfilm + 2) = f(εf - 1)/(εf + 2), where f is the volume fraction of the fungi contained in the films45,46,47. Here it is important to estimate the volume fractions reasonably in order to obtain the dielectric constants of the individual fungi accurately. In the case of penicillium film, we extracted f of 0.28–0.62 by measuring the total mass and volume of the film and from the information on the mass of penicillium (ranging 58–129 pg, depending on the wetting condition)48. On the other hand, the volume fraction f of the yeast film was chosen to be 0.64–0.78, assuming that it consists of the closely packed spheres49. Fig. 5c shows the complex dielectric constants of the individual penicillium as extracted from the THz transmission experiments, which shows the upper and lower bounds corresponding to the volume fractions of 0.28 and 0.62, respectively, yielding the real part of the dielectric constants as 1.37–1.94 at 0.8 THz. Similarly, the dielectric constant of yeast is determined to be 5.38–8.54. The dielectric constant of the yeast (which is significantly higher than that of penicillium) is in accordance with the results shown in Fig. 4, in which the resonant frequency shift for a given number density is higher for the yeasts as compared to the penicillia. However, their relative difference in εf −1 is somewhat larger than the value expected from Fig. 4. It is likely that other parameters such as the shape of the individual fungi and the wetting conditions need be considered further in order to explain the discrepancy, which requires future study. We also measured the dielectric constant of E. coli in order to explain the blue shift of resonant peak in a solution environment [Supplementary Figure S4].
Our experimental findings were analyzed by using the finite-difference time-domain simulations, as shown in Fig. 6. We used the metamaterial patterns (described by gray lines) with the geometric parameters similar to those in our experiments, as shown by the three-dimensional (left) and two-dimensional cross-sectional plots (right) in Fig. 6a. In order to reproduce the effects of the fungi deposition, we added a series of dielectric spheres (which represent the fungi) in the gap areas of the metamaterials. Five dielectric spheres, each with the diameter of 2 μm, were used in this case. The color images overlaid in the patterns are the representative plots showing the electric field strength at the resonant frequency of 0.73 THz. It is clear that the electric fields are strongly localized in the gap area as mentioned before, whereas the fields are strongly modified in the presence of the dielectric spheres. Fig. 6b shows the typical transmission spectra of the simulation results with the dielectric constants of the spheres set to εf = 1 (air) and εf = 8 (fungi), respectively.
Results of finite-difference time-domain simulations.
(a) 3D plot of the electric field strength at the resonant frequency of 0.73 THz, when the series of five dielectric spheres (with εf = 8) are placed in the micro-gap of the metamaterials. Shown on the right is a 2D cross-sectional image taken along the dashed line in the 3D plot. (b) THz transmission spectra for the cases in which the dielectric constant of each of the five spheres are of εf = 1 (blue line) and εf = 8 (red line), respectively. (c) A plot of resonant frequency shift as a function of the number of spheres, for five different εf's ranging from 2 to 10.
A clear red-shift in the resonant frequency is observed for the case of εf = 8 (with fungi) as compared to the case of εf = 1 (without fungi), consistent with the experimental findings. Finally, we show a plot of the resonant frequency shift as a function of the number of spheres in the gap areas, for different dielectric constants ranging from 2 to 10 (Fig. 6c). The resonant frequency shift increases linearly with the increasing number of fungi in the gap areas, which is apparently higher for the higher dielectric constants (See Supplementary Figure S6). Results of these simulations successfully reproduce our experimental findings. We also found that the inductive-capacitive resonant peak is not influenced noticeably by the dielectric materials located outside of the gap area (See Supplementary Figure S7). It remains unclear why the magnitude of the resonant frequency shift in the simulation is rather smaller than the one that is obtained in the experiments. The discrepancy is probably because we used photolithographic methods with limited spatial resolution (see Fig. 1b) and possibly is due to approximating the shape of the individual fungi as spheres.
We would like to mention that our technique is sensitive to the surface number density of the fungi and bacteria located at the surface, whereas most of the contemporary techniques refer the volume density50,51. In fact, there is a tradeoff between the detection speed and the sensitivity. In our case, the sensitivity depends on the deposition time from a solution in sensing bacteria as shown in Fig. 3. For the detection of E. coli in drinking water, the latest culture-based methods report the detection limit of 50 CFU/ml in 3 hr, in which only colony-forming units (CFU) are counted52. By simply counting the number density of bacteria in the solution, we can estimate our detection limit to be ~107 units/ml (including non-colony-forming units) for 1 hr of E. coli deposition. Therefore, improving the capture efficiency of these microorganisms at the surface and near the gap-area in particular, will be essential for improving the sensitivity and the speed of the THz metamaterial sensing. Besides, the sensitivity can be improved further by adopting advanced designs with higher Q-factors53,54, by using the substrate of lower refractive index and by increasing the metal thickness so that it is comparable to the size of the microorganisms.
To conclude, we found that the THz metamaterials can be used to detect various microorganisms such as molds, yeasts and bacteria. A clear shift in the inductive-capacitive resonant frequency is observed following the deposition of microorganisms and arises due to the change in the effective dielectric constant in a gap area of the metamaterials patterns. The resonant frequency shift is higher for the larger dielectric constants, which was confirmed by the dielectric constant measurements of individual fungi and by the numerical simulations. Our technique can be applied to various viable and living microorganisms that dwell in aqueous environments, as well as in ambient conditions, because it is highly sensitive to the substances located near the surface, allowing us to use a thin water layer without suffering from the poor transmission in conventional THz spectroscopies. The THz metamaterial sensing is a universal method because it is based on the dielectric sensing, while a selective detection is also possible by functionalizing the substrates with antibodies specific to the target substances. Our approach is likely to constitute an important step toward the fabrication of the highly sensitive biosensors and lab-on-a-chip devices, enabling the high-speed on-site detection of hazardous substances in various environments.
Methods
Terahertz time-domain spectroscopy
The real-time THz transmission amplitudes of the metamaterials with fungi were measured with a conventional THz time-domain spectroscopy (THz-TDS) setup. A femtosecond laser at λ = 800 nm is incident on the photoconductive antenna which emits a linearly polarized THz pulse. Subsequently, this THz pulse is focused on the metamaterials with ~1 mm spot diameter under ambient conditions. Time traces of the transmitted THz electric field both in amplitude and phase were measured by varying the time delay between the 800 nm probe beam and the THz pulse. THz spectrum is taken by applying a fast Fourier transform (FFT) to the time trace and normalized with respect to the reference. The typical spectral resolution was ~30 GHz for a temporal scan range of 33 ps.
Fabrication of Metamaterial Patterns
Metamaterial patterns were prepared by using a conventional photo-lithography method on a high-resistivity Si substrate (n-type, resistivity > 6000 Ω·cm and thickness of 550 μm). Cr (2 nm) and Au (98 nm) metal films were deposited by an e-beam evaporator in order to define the arrays of split ring resonator patterns with a linewidth of 4 μm, outer dimension of 36 μm × 36 μm and gap size of 3 μm. The periodicities of array patterns were 86 μm (Fig. 2 and 4) and 50 μm (Fig. 3).
Preparation of fungi
Penicillium chrysogenum (KACC 40399; penicillia), Neurospora sitophila (KACC 40972; neurospora), Aspergillus niger (KACC 40280; niger) and Saccharomyces cerevisiae (yeasts) were grown by a streaking on medium method followed by the incubation at 37°C for 2 days. All the fungi were obtained from the Korean Agricultural Culture Collection (KACC). The culture media used for the penicillia, yeasts, neurospora and niger were V8 juice agar, yeast peptone dextrose, potato dextrose agar and malt extract agar, respectively. Escherichia coli BL21(DE3) (E. coli) were grown by a similar method on the medium of luria broth.
Surface Functionalization and Deposition of E. coli
We begin with surface functionalization by immersing the metamaterials substrate in (3-Aminopropyl)triethoxysilane (APTS):toluene (2:1000) solutions for 3 hours. E. coli antibodies (Abcam) were immobilized on Si substrate with metamaterial patterns by immersing the substrate in antibody: phosphate buffered saline (PBS) 1× in 200 μg/ml for 3 hours. After antibody immobilization, E. coli were deposited from the E. coli: PBS solution in 100 μg/ml for 1 hour, followed by a rinsing with distilled water to eliminate remaining surface non-linked E. coli. The patterns were enclosed by a quartz cover glass (with a thickness of 170 μm) and the water layer thickness was fixed at 55 μm by using a spacer.
Dielectric Measurement of fungi and E. coli
The films for the dielectric measurement were prepared by stacking the large amount of fungi layer by layer on a cellulose membrane (with a pore size of 200 nm and a thickness of 100 μm), as a result, the thickness of the penicillia and yeasts films reached 350 μm and 125 μm, respectively. The membrane substrate is almost transparent to the THz waves, whose refractive index of the membrane substrate is close to unity in the THz frequency range55. By measuring both the amplitudes and phases of the transmitted THz pulses, we extracted the complex dielectric constants of the films, from which we extracted those of the individual fungi by using the Maxwell-Garnett model. We performed the same procedures on the three different films for both fungi and found the similar dielectric constants each time.
Finite Difference Time-Domain (FDTD) Simulation
To predict the electromagnetic behavior of the metamaterials, the structure is simulated by using CST MICROWAVE STUDIO.
References
Makimura, K., Murayama, S. Y. & Yamaguchi, H. Detection of a wide range of medically important fungi by the polymerase chain reaction. J. Med. Microbiol. 40, 358–364 (1994).
Belgrader, P. et al. PCR detection of bacteria in seven minutes. Science 284, 449–450 (1999).
Josephson, K. L., Gerba, C. P. & Pepper, I. L. Polymerase chain reaction detection of nonviable bacterial pathogens. Appl. Environ. Microb. 59, 3513–3515 (1993).
Vanhee, L. M. E., D'Haese, E., Cools, I., Nelis, H. J. & Coenye, T. Detection of Bacteria, Viruses, Parasites and Fungi: Detection and Quantification of Bacteria and Fungi Using Solid-Phase Cytometry. (Springer, 2010).
Amann, R. I. et al. Combination of 16S rRNA-targeted oligonucleotide probes with flow cytometry for analyzing mixed microbial populations. Appl. Environ. Microbiol. 56, 1919–1925 (1990).
Ferguson, B. & Zhang, X. C. Materials for terahertz science and technology. Nat. Mater. 1, 26–33 (2002).
Menikh, A., MacColl, R., Mannella, C. A. & Zhang, X. C. Terahertz biosensing technology: Frontiers and progress. ChemPhysChem 3, 655–658 (2002).
Markelz, A. G., Roitberg, A. & Heilweil, E. J. Pulsed terahertz spectroscopy of DNA, bovine serum albumin and collagen between 0.1 and 2.0 THz. Chem. Phys. Lett. 320, 42–48 (2000).
Mickan, S. P. et al. Label-free bioaffinity detection using terahertz technology. Phys. Med. Biol. 47, 3789 (2002).
Nagel, M., Richter, F., Haring-Bolivar, P. & Kurz, H. A functionalized THz sensor for marker-free DNA analysis. Phys. Med. Biol. 48, 3625 (2003).
Woodward, R. M., Wallace, V. P., Arnone, D. D., Linfield, E. H. & Pepper, M. Terahertz pulsed imaging of skin cancer in the time and frequency domain. J. Biol. Phys. 29, 257–259 (2003).
Menikh, A., Mickan, S. P., Liu, H., MacColl, R. & Zhang, X. C. Label-free amplified bioaffinity detection using terahertz wave technology. Biosens. Bioelectron. 20, 658–662 (2004).
George, P. A. et al. Microfluidic devices for terahertz spectroscopy of biomolecules. Opt. Express 16, 1577–1582 (2008).
Alexandrov, B. S., Gelev, V., Bishop, A. R., Usheva, A. & Rasmussen, K. Ø. DNA breathing dynamics in the presence of a terahertz field. Phys. Lett. A 374, 1214–1217 (2010).
Park, H. R. et al. Colossal absorption of molecules inside single terahertz nano antennas. Nano Lett. 13, 1782–1786 (2013).
Seco-Martorell, C. et al. Goyas artwork imaging with Terahertz waves. Opt. Express 21, 17800–17805 (2013).
Zhao, P., Ragam, S., Ding, Y. J. & Zotova, I. B. Compact and portable terahertz source by mixing two frequencies generated simultaneously by a single solid-state laser. Opt. Lett. 35, 3979–3981 (2010).
Berrier, A., Schaafsma, M. C., Nonglaton, G., Bergquist, J. & Rivas, J. G. Selective detection of bacterial layers with terahertz plasmonic antennas. Biomed. Opt. Express 3, 2937 (2012).
Pendry, J. B., Holden, A. J., Robbins, D. J. & Stewart, W. J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory 47, 2075–2084 (1999).
Shelby, R. A., Smith, D. R. & Schultz, S. Experimental verification of a negative index of refraction. Science 292, 77–79 (2001).
Liu, Z., Lee, H., Xiong, Y., Sun, C. & Zhang, X. Far-field optical hyperlens magnifying sub-diffraction-limited objects. Science 315, 1686–1686 (2007).
Pendry, J. B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966 (2000).
Smolyaninov, I. I., Hung, Y. J. & Davis, C. C. Magnifying superlens in the visible frequency range. Science 315, 1699–1701 (2007).
Pendry, J. B., Schurig, D. & Smith, D. R. Controlling electromagnetic fields. Science 312, 1780–1782 (2006).
Schurig, D. et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980 (2006).
Hong, J. T. et al. Dielectric Constant Engineering of Single-Walled Carbon Nanotube Films for Metamaterials and Plasmonic Devices. J. Phys. Chem. Lett. 4, 3950–3957 (2013).
Chen, T., Li, S. & Sun, H. Metamaterials application in sensing. Sensors 12, 2742–2765 (2012).
Chang, Y. T., Lai, Y. C., Li, C. T., Chen, C. K. & Yen, T. J. A multi-functional plasmonic biosensor. Opt. Express 18, 9561–9569 (2010).
Park, D. J. et al. Terahertz near-field enhancement in narrow rectangular apertures on metal film. Opt. Express 17, 12493–12501 (2009).
Seo, M. A. et al. Terahertz field enhancement by a metallic nano slit operating beyond the skin-depth limit. Nature Photon. 3, 152–156 (2009).
Berrier, A. et al. Detection of deep-subwavelength dielectric layers at terahertz frequencies using semiconductor plasmonic resonators. Opt. Express 20, 5052–5060 (2012).
Yen, T. J. et al. Terahertz magnetic response from artificial materials. Science 303, 1494–1496 (2004).
Chen, H. T. et al. Active terahertz metamaterial devices. Nature 444, 597–600 (2006).
Chen, H. T. et al. Electromagnetic metamaterials for terahertz applications. Terahertz Sci. Technol. 1, 42–50 (2008).
Tao, H. et al. Metamaterials on Paper as a Sensing Platform. Adv. Mater. 23, 3197–3201 (2011).
O’Hara, J. F., Withayachumnankul, W. & Al-Naib, I. A review on thin-film sensing with terahertz waves. J. Infrared Millim. Terahertz Waves 33, 245–291 (2012).
Tao, H. et al. Silk-Based Conformal, Adhesive, Edible Food Sensors. Adv. Mater. 24, 1067–1072 (2012).
O'Hara, J. F. et al. Thin-film sensing with planar terahertz metamaterials: sensitivity and limitations. Opt. Express 16, 1786–1795 (2008).
Azad, A. K., Dai, J. & Zhang, W. Transmission properties of terahertz pulses through subwavelength double split-ring resonators. Opt. lett. 31, 634–636 (2006).
Hong, J. T. et al. Terahertz conductivity of reduced graphene oxide films. Opt. Express 21, 7633–7640 (2013).
Park, D. J. et al. Resonant transmission of terahertz waves through metallic slot antennas on various dielectric substrates. Curr. Appl. Phys. 13, 753–757 (2013).
Recio-Sanchez, G. et al. Surface functionalization of nanostructured porous silicon by APTS: toward the fabrication of electrical biosensors of bacterium Escherichia coli. Curr. Nanosci. 7, 178–182 (2011).
Rønne, C., Thrane, L., Åstrand, P. O., Wallqvist, A. & Mikkelsen, K. V. Investigation of the temperature dependence of dielectric relaxation in liquid water by THz reflection spectroscopy and molecular dynamics simulation. J. Chem. Phys 107, 5319 (1997).
Nugaeva, N. et al. Micromechanical cantilever array sensors for selective fungal immobilization and fast growth detection. Biosens. Bioelectron. 21, 849–856 (2005).
Garnett, J. C. M. Colours in Metal Glasses and in Metallic Films. Proc. R. Soc. Lond. 73, 443–445 (1904).
Garnett, J. C. M. Colours in metal glasses, in metallic films and in metallic solutions. II. Philos. Trans. R. Soc. 237–288 (1906).
Walther, M. et al. Terahertz conductivity of thin gold films at the metal-insulator percolation transition. Phys. Rev. B 76, 125408 (2007).
Sansing, G. A. & Ciegler, A. Mass propagation of conidia from several Aspergillus and Penicillium species. Appl. Microbiol. 26, 830 (1973).
Weitz, D. A. Packing in the spheres. Science 303, 968–969 (2004).
Caygill, R. L., Blair, G. E. & Millner, P. A. A review on viral biosensors to detect human pathogens. Anal. Chim. Acta. 681, 8–15 (2010).
Sidjabat, H., Cooper, M. A. & Ranzoni, A. Nanoparticle sample preparation and mass spectrometry for rapid diagnosis of microbial infections. Microbiol. Australia 34, 170–174 (2013).
Aydin, M. et al. Rapid and Sensitive Detection of Escherichia coli O157: H7 in Milk and Ground Beef Using Magnetic Bead–Based Immunoassay Coupled with Tyramide Signal Amplification. J. Food Prot. 77, 100–105 (2014).
Jansen, C., Al-Naib, I. A. I., Born, N. & Koch, M. Terahertz metasurfaces with high Q-factors. Appl. Phys. Lett. 98, 051109 (2011).
Li, J. et al. Mechanically tunable terahertz metamaterials. Appl. Phys. Lett. 102, 121101 (2013).
Hong, J. T. et al. Terahertz wave applications of single-walled carbon nanotube films with high shielding effectiveness. Appl. Phys. Express 5, 5102 (2012).
Acknowledgements
This work was supported by Mid-career Researcher Programs (2011-0016173), PRC Program (2009-0094046) and Public Welfare & Safety Research Program (2011-0020819) through National Research Foundation grant funded by the Korea Government. This work was also supported by the Joint Research Project of the Korea Research Council for Industrial Science and Technology (ISTK).
Author information
Authors and Affiliations
Contributions
Y.H.A. conceived and designed the experiments. S.J.P. and J.T.H. fabricated metamaterials and performed THz experiments. S.J.C. and H.S.K. provided fungi and bacteria samples. W.K.P. and S.T.H. participated in FDTD analysis. All authors including J.Y.P., S.L. and D.S.K. discussed the results and participated in writing the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Dataset
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Park, S., Hong, J., Choi, S. et al. Detection of microorganisms using terahertz metamaterials. Sci Rep 4, 4988 (2014). https://doi.org/10.1038/srep04988
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04988