Abstract
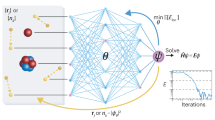
The Schrödinger equation describes the quantum-mechanical behaviour of particles, making it the most fundamental equation in chemistry. A solution for a given molecule allows computation of any of its properties. Finding accurate solutions for many different molecules and geometries is thus crucial to the discovery of new materials such as drugs or catalysts. Despite its importance, the Schrödinger equation is notoriously difficult to solve even for single molecules, as established methods scale exponentially with the number of particles. Combining Monte Carlo techniques with unsupervised optimization of neural networks was recently discovered as a promising approach to overcome this curse of dimensionality, but the corresponding methods do not exploit synergies that arise when considering multiple geometries. Here we show that sharing the vast majority of weights across neural network models for different geometries substantially accelerates optimization. Furthermore, weight-sharing yields pretrained models that require only a small number of additional optimization steps to obtain high-accuracy solutions for new geometries.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
9,800 Yen / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
¥11,900 per year
only ¥992 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
All data in this manuscript were generated using the Python package DeepErwin or the quantum-chemistry code MOLPRO as described in Methods. All data required to perform the reported calculations as well as the processed data that was used to generate figures are available on Code Ocean42. Source data are provided with this paper.
Code availability
The DeepErwin package alongside a detailed documentation is available on the Python Package Index (PyPI) and GitHub (https://github.com/mdsunivie/deeperwin) under the MIT license. All codes and configuration files that were used to perform the reported calculations are also available on Code Ocean42.
References
Han, J., Zhang, L. & E, W. Solving many-electron Schrödinger equation using deep neural networks. J. Comput. Phys. 399, 108929 (2019).
Hermann, J., Schätzle, Z. & Noé, F. Deep-neural-network solution of the electronic Schrödinger equation. Nat. Chem. 12, 891–897 (2020).
Manzhos, S. Machine learning for the solution of the Schrödinger equation. Mach. Learn. Sci. Technol. 1, 013002 (2020).
Pfau, D., Spencer, J. S., Matthews, A. G. D. G. & Foulkes, W. M. C. Ab initio solution of the many-electron Schrödinger equation with deep neural networks. Phys. Rev. Res. 2, 033429 (2020).
Wilson, M., Gao, N., Wudarski, F., Rieffel, E. & Tubman, N. M. Simulations of state-of-the-art fermionic neural network wave functions with diffusion Monte Carlo. Phys. Rev. Res. 4, 013021 (2021).
Bartlett, R. J. & Musiał, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 79, 291–352 (2007).
Spencer, J. S., Pfau, D., Botev, A. & Foulkes, W. M. C. Better, faster fermionic neural networks. Preprint at https://arxiv.org/abs/2011.07125 (2020).
Unke, O. T. et al. Machine learning force fields. Chem. Rev. 121, 10142–10186 (2021).
Behler, J. Four generations of high-dimensional neural network potentials. Chem. Rev. 121, 10037–10072 (2021).
Kirkpatrick, J. et al. Pushing the frontiers of density functionals by solving the fractional electron problem. Science 374, 1385–1389 (2021).
Westermayr, J. & Marquetand, P. Machine learning for electronically excited states of molecules. Chem. Rev. 121, 9873–9926 (2020).
Schütt, K. T., Gastegger, M., Tkatchenko, A., Müller, K.-R. & Maurer, R. J. Unifying machine learning and quantum chemistry with a deep neural network for molecular wavefunctions. Nat. Commun. 10, 5024 (2019).
Bogojeski, M., Vogt-Maranto, L., Tuckerman, M. E., Müller, K.-R. & Burke, K. Quantum chemical accuracy from density functional approximations via machine learning. Nat. Commun. 11, 5223 (2020).
Faber, F. A. et al. Prediction errors of molecular machine learning models lower than hybrid DFT error. J. Chem. Theory Comput. 13, 5255–5264 (2017).
Devlin, J., Chang, M.-W., Lee, K. & Toutanova, K. Bert: pre-training of deep bidirectional transformers for language understanding. Preprint at https://arxiv.org/abs/1810.04805 (2018).
Tan, C. et al. A survey on deep transfer learning. In International Conference on Artificial Neural Networks 270–279 (Springer, 2018).
Matthews, D. A. Analytic gradients of approximate coupled cluster methods with quadruple excitations. J. Chem. Theory Comput. 16, 6195–6206 (2020).
Schütt, K. et al. SchNet: a continuous-filter convolutional neural network for modeling quantum interactions. In Proc. 31st Conference on Neural Information Processing Systems (eds Guyon, I. et al.) 992–1002 (Curran Associates, 2017).
Ma, A., Towler, M. D., Drummond, N. D. & Needs, R. J. Scheme for adding electron–nucleus cusps to Gaussian orbitals. J. Chem. Phys. 122, 224322 (2005).
Martens, J. & Grosse, R. Optimizing neural networks with kronecker-factored approximate curvature. In International Conference on Machine Learning 2408–2417 (PMLR, 2015).
Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. Preprint at https://arxiv.org/abs/1412.6980 (2014).
Alijah, A. & Varandas, A. J. C. H4+: what do we know about it? J. Chem. Phys. 129, 034303 (2008).
Feynman, R. P. Forces in molecules. Phys. Rev. 56, 340–343 (1939).
Peierls, R. E. & Peierls, R. S. Quantum Theory of Solids (Oxford Univ. Press, 1955).
Pulay, P. Ab initio calculation of force constants and equilibrium geometries in polyatomic molecules. Mol. Phys. 17, 197–204 (1969).
Gao, N. & Günnemann, S. Ab-initio potential energy surfaces by pairing GNNs with neural wave functions. In International Conference on Learning Representations (2022).
Ríos, P. L., Ma, A., Drummond, N. D., Towler, M. D. & Needs, R. J. Inhomogeneous backflow transformations in quantum Monte Carlo calculations. Phys. Rev. E 74, 066701 (2006).
Kato, T. On the eigenfunctions of many-particle systems in quantum mechanics. Commun. Pure Appl. Math. 10, 151–177 (1957).
Liu, D. C. & Nocedal, J. On the limited memory bfgs method for large scale optimization. Math. Prog. 45, 503–528 (1989).
Ceperley, D., Chester, G. V. & Kalos, M. H. Monte Carlo simulation of a many-fermion study. Phys. Rev. B 16, 3081–3099 (1977).
Hastings, W. K. Monte carlo sampling methods using Markov chains and their applications. Biometrika 57, 97–109 (1970).
Chiesa, S., Ceperley, D. M. & Zhang, S. Accurate, efficient, and simple forces computed with quantum monte carlo methods. Phys. Rev. Lett. 94, 036404 (2005).
Kalos, M. H. & Whitlock, P. A. Monte Carlo Methods (Wiley, 1986); https://cds.cern.ch/record/109491
Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R. & Schütz, M. MOLPRO: a general-purpose quantum chemistry program package. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2, 242–253 (2012).
Werner, H.-J. et al. MOLPRO, version 2012.1. A package of ab initio programs (MOLPRO, 2012); https://www.molpro.net
Adler, T. B., Knizia, G. & Werner, H.-J. A simple and efficient CCSD(T)-F12 approximation. J. Chem. Phys. 127, 221106 (2007).
Shiozaki, T., Knizia, G. & Werner, H.-J. Explicitly correlated multireference configuration interaction: MRCI-F12. J. Chem. Phys. 134, 034113 (2011).
Peterson, K. A., Adler, T. B. & Werner, H.-J. Systematically convergent basis sets for explicitly correlated wavefunctions: the atoms H, He, B–Ne, and Al–Ar. J. Chem. Phys. 128, 084102 (2008).
Hill, J. G., Mazumder, S. & Peterson, K. A. Correlation consistent basis sets for molecular core-valence effects with explicitly correlated wave functions: the atoms B–Ne and Al–Ar. J. Chem. Phys. 132, 054108 (2010).
Langhoff, S. R. & Davidson, E. R. Configuration interaction calculations on the nitrogen molecule. Int. J. Quantum Chem. 8, 61–72 (1974).
Sun, Q. et al. PySCF: the Python-based simulations of chemistry framework. Wiley Interdiscip. Rev. Comput. Mol. Sci. 8, e1340 (2018).
Scherbela, M., Reisenhofer, R., Gerard, L., Marquetand, P. & Grohs, P. DeepErwin—a framework for solving the Schrödinger equation with deep neural networks. CodeOcean https://doi.org/10.24433/CO.8193370.v1 (2022).
Acknowledgements
We gratefully acknowledge financial support from the following grants: Austrian Science Fund FWF-I-3403 (L.G.), FWF-M-2528 (R.R.) and WWTF-ICT19-041 (L.G.). The computational results have been achieved using the Vienna Scientific Cluster (VSC). The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.
Author information
Authors and Affiliations
Contributions
P.G., P.M. and R.R. conceived the project. M.S., L.G. and R.R. developed the detailed method. M.S. and L.G. wrote the Python code with contributions from R.R. The numerical experiments were designed and performed by M.S., L.G. and P.M. with support from R.R. R.R., M.S. and L.G. wrote the manuscript with input from P.G. and P.M. P.G. supervised the project. R.R. and P.G. obtained funding.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Computational Science thanks Huan Tran, Linfeng Zhang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available. Primary Handling Editor: Jie Pan, in collaboration with the Nature Computational Science team.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–3 and Tables 1–3.
Supplementary Data 1
Source data for Supplementary Fig. 1.
Supplementary Data 2
Source data for Supplementary Fig. 2.
Supplementary Data 3
Source data for Supplementary Fig. 3.
Source data
Source Data Fig. 1
Statistical source data for Fig. 1b.
Source Data Fig. 2
Statistical source data for Fig. 2.
Source Data Fig. 3
Statistical source data for Fig. 3.
Source Data Fig. 4
Statistical source data for Fig. 4.
Source Data Fig. 5
Statistical source data for Fig. 5.
Rights and permissions
About this article
Cite this article
Scherbela, M., Reisenhofer, R., Gerard, L. et al. Solving the electronic Schrödinger equation for multiple nuclear geometries with weight-sharing deep neural networks. Nat Comput Sci 2, 331–341 (2022). https://doi.org/10.1038/s43588-022-00228-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s43588-022-00228-x
This article is cited by
-
A computational framework for neural network-based variational Monte Carlo with Forward Laplacian
Nature Machine Intelligence (2024)
-
Towards a transferable fermionic neural wavefunction for molecules
Nature Communications (2024)
-
Employing neural density functionals to generate potential energy surfaces
Journal of Molecular Modeling (2024)
-
Electronic excited states in deep variational Monte Carlo
Nature Communications (2023)
-
Electron transfer rules of minerals under pressure informed by machine learning
Nature Communications (2023)