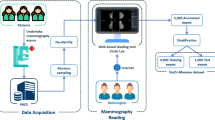
Abstract
Breast cancer remains a global challenge, causing over 600,000 deaths in 2018 (ref. 1). To achieve earlier cancer detection, health organizations worldwide recommend screening mammography, which is estimated to decrease breast cancer mortality by 20–40% (refs. 2,3). Despite the clear value of screening mammography, significant false positive and false negative rates along with non-uniformities in expert reader availability leave opportunities for improving quality and access4,5. To address these limitations, there has been much recent interest in applying deep learning to mammography6,7,8,9,10,11,12,13,14,15,16,17,18, and these efforts have highlighted two key difficulties: obtaining large amounts of annotated training data and ensuring generalization across populations, acquisition equipment and modalities. Here we present an annotation-efficient deep learning approach that (1) achieves state-of-the-art performance in mammogram classification, (2) successfully extends to digital breast tomosynthesis (DBT; ‘3D mammography’), (3) detects cancers in clinically negative prior mammograms of patients with cancer, (4) generalizes well to a population with low screening rates and (5) outperforms five out of five full-time breast-imaging specialists with an average increase in sensitivity of 14%. By creating new ‘maximum suspicion projection’ (MSP) images from DBT data, our progressively trained, multiple-instance learning approach effectively trains on DBT exams using only breast-level labels while maintaining localization-based interpretability. Altogether, our results demonstrate promise towards software that can improve the accuracy of and access to screening mammography worldwide.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
9,800 Yen / 30 days
cancel any time
Subscription info for Japanese customers
We have a dedicated website for our Japanese customers. Please go to natureasia.com to subscribe to this journal.
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
Applications for access of the OMI-DB can be completed at https://medphys.royalsurrey.nhs.uk/omidb/getting-access/. The DDSM can be accessed at http://www.eng.usf.edu/cvprg/Mammography/Database.html. The remainder of the datasets used are not currently permitted for public release by their respective Institutional Review Boards.
Code availability
Code to enable model evaluation for research purposes via an evaluation server has been made available at https://github.com/DeepHealthAI/nature_medicine_2020.
References
Bray, F. et al. Global cancer statistics 2018: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 68, 394–424 (2018).
Berry, D. A. et al. Effect of screening and adjuvant therapy on mortality from breast cancer. N. Engl. J. Med. 353, 1784–1792 (2005).
Seely, J. M. & Alhassan, T. Screening for breast cancer in 2018—what should we be doing today? Curr. Oncol. 25, S115–S124 (2018).
Majid, A. S., Shaw De Paredes, E., Doherty, R. D., Sharma, N. R. & Salvador, X. Missed breast carcinoma: pitfalls and pearls. Radiographics 23, 881–895 (2003).
Rosenberg, R. D. et al. Performance benchmarks for screening mammography. Radiology 241, 55–66 (2006).
Yala, A., Lehman, C., Schuster, T., Portnoi, T. & Barzilay, R. A deep learning mammography-based model for improved breast cancer risk prediction. Radiology 292, 60–66 (2019).
Yala, A., Schuster, T., Miles, R., Barzilay, R. & Lehman, C. A deep learning model to triage screening mammograms: a simulation study. Radiology 293, 38–46 (2019).
Conant, E. F. et al. Improving accuracy and efficiency with concurrent use of artificial intelligence for digital breast tomosynthesis. Radiol. Artif. Intell. 1, e180096 (2019).
Rodriguez-Ruiz, A. et al. Stand-alone artificial intelligence for breast cancer detection in mammography: comparison with 101 radiologists. J. Natl Cancer Inst. 111, 916–922 (2019).
Rodríguez-Ruiz, A. et al. Detection of breast cancer with mammography: effect of an artificial intelligence support system. Radiology 290, 305–314 (2019).
Wu, N. et al. Deep neural networks improve radiologists’ performance in breast cancer screening. IEEE Trans. Med. Imaging 39 1184–1194 (2019).
Ribli, D., Horváth, A., Unger, Z., Pollner, P. & Csabai, I. Detecting and classifying lesions in mammograms with deep learning. Sci. Rep. 8, 4165 3 (2018).
Kooi, T. et al. Large scale deep learning for computer aided detection of mammographic lesions. Med. Image Anal. 35, 303–312 (2017).
Geras, K. J. et al. High-resolution breast cancer screening with multi-view deep convolutional neural networks. Preprint at https://arxiv.org/abs/1703.07047 (2017).
Lotter, W., Sorensen, G., and Cox, D. A multi-scale CNN and curriculum learning strategy for mammogram classification. in Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support (eds. Cardoso, M. J. et al.) (2017).
Schaffter, T. et al. Evaluation of combined artificial intelligence and radiologist assessment to interpret screening mammograms. JAMA Netw. Open 3, e200265 (2020).
McKinney, S. M. et al. International evaluation of an AI system for breast cancer screening. Nature 577, 89–94 (2020).
Kim, H.-E. et al Changes in cancer detection and false-positive recall in mammography using artificial intelligence: a retrospective, multireader study. Lancet Digit. Health 2, e138–e148 (2020).
Kopans, D. B. Digital breast tomosynthesis from concept to clinical care. Am. J. Roentgenol. 202, 299–308 (2014).
Saarenmaa, I. et al. The visibility of cancer on earlier mammograms in a population-based screening programme. Eur. J. Cancer 35, 1118–1122 7 (1999).
Ikeda, D. M., Birdwell, R. L., O’Shaughnessy, K. F., Brenner, R. J. & Sickles, E. A. Analysis of 172 subtle findings on prior normal mammograms in women with breast cancer detected at follow-up screening. Radiology 226, 494–503 (2003).
Hoff, S. R. et al. Missed and true interval and screen-detected breast cancers in a population based screening program. Acad. Radiol. 18, 454–460 (2011).
Fenton, J. J. et al. Influence of computer-aided detection on performance of screening mammography. N. Engl. J. Med. 356, 1399–1409 4 (2007).
Lehman, C. D. et al. Diagnostic accuracy of digital screening mammography with and without computer aided detection. JAMA Intern. Med. 33, 839–841 (2016).
Henriksen, E. L., Carlsen, J. F., Vejborg, I. M., Nielsen, M. B. & Lauridsen, C. A. The efficacy of using computer-aided detection (CAD) for detection of breast cancer in mammography screening: a systematic review. Acta Radiol. 60, 13–18 1 (2019).
Tchou, P. M. et al. Interpretation time of computer-aided detection at screening mammography. Radiology 257, 40–46 (2010).
Bowser, D., Marqusee, H., Koussa, M. E. & Atun, R. Health system barriers and enablers to early access to breast cancer screening, detection, and diagnosis: a global analysis applied to the MENA region. Public Health 152, 58–74 (2017).
Fan, L. et al. Breast cancer in China. Lancet Oncol. 15, e279–e289 (2014).
Heath, M., Bowyer, K., Kopans, D., Moore, R. & Kegelmeyer W. P. The digital database for screening mammography. in Proceedings of the 5th International Workshop on Digital Mammography (ed Yaffe, M. J.) 212–218 (2001).
Halling-Brown, M. D. et al. OPTIMAM mammography image database: a large scale resource of mammography images and clinical data. Preprint at https://arxiv.org/abs/2004.04742 (2020).
Deng, J. et al. ImageNet: a large-scale hierarchical image database. in Conference on Computer Vision and Pattern Recognition (2009).
Wu, K. et al. Validation of a deep learning mammography model in a population with low screening rates. in Fair ML for Health Workshop. Neural Information Processing Systems (2019).
Sickles, E., D’Orsi, C. & Bassett, L. ACR BI-RADS Atlas, Breast Imaging Reporting and Data System 5th edn (American College of Radiology, 2013).
Hart, D., Shochat, E. & Agur, Z. The growth law of primary breast cancer as inferred from mammography screening trials data. Br. J. Cancer 78, 382–387 (1998).
Weedon-Fekjær, H., Lindqvist, B. H., Vatten, L. J., Aalen, O. O. & Tretli, S. Breast cancer tumor growth estimated through mammography screening data. Breast Cancer Res. 10, R41 (2008).
Lehman, C. D. et al. National performance benchmarks for modern screening digital mammography: update from the Breast Cancer Surveillance Consortium. Radiology 283, 49–58 (2017).
Bae, J.-M. & Kim, E. H. Breast density and risk of breast cancer in Asian women: a meta-analysis of observational studies. J. Preventive Med. Public Health 49, 367 (2016).
Park, S. H. Diagnostic case-control versus diagnostic cohort studies for clinical validation of artificial intelligence algorithm performance. Radiology 290, 272–273 (2018).
Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 9, 62–66 (1979).
He, K., Zhang, X., Ren, S. & Sun, J. Deep residual learning for image recognition. in The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 770–778, (2016).
Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. in The 3rd International Conference on Learning Representations (ICLR) (2015).
Lin, T., Goyal, P., Girshick, R., He, K. & Dollár, P. Focal loss for dense object detection. in The IEEE International Conference on Computer Vision (ICCV), 2999–3007 (2017).
Gallas, B. D. et al. Impact of prevalence and case distribution in lab-based diagnostic imaging studies. J. Med. Imaging 6, 1 1 (2019).
Evans, K. K., Birdwell, R. L. & Wolfe, J. M. If you don’t find it often, you often don’t find it: why some cancers are missed in breast cancer screening. PLoS ONE 8, e64366 (2013).
DeLong, E. R., DeLong, D. M. & Clarke-Pearson, D. L. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 44, 837–845 (1988).
Acknowledgements
We are grateful to S. Venkataraman, E. Ghosh, A. Newburg, M. Tyminski and N. Amornsiripanitch for participation in the study. We also thank C. Lee, D. Kopans, E. Pisano, P. Golland and J. Holt for guidance and valuable discussions. We additionally thank T. Witzel, I. Swofford, M. Tomlinson, J. Roubil, J. Watkins, Y. Wu, H. Tan and S. Vedantham for assistance in data acquisition and processing. This work was supported in part by grants from the National Cancer Institute (1R37CA240403-01A1 and 1R44CA240022-01A1) and the National Science Foundation (SBIR 1938387) received by DeepHealth. All of the non-public datasets used in the study were collected retrospectively and de-identified under IRB-approved protocols in which informed consent was waived.
Author information
Authors and Affiliations
Contributions
W.L., B.H., G.R.V. and A.G.S. conceived of the research design. W.L., B.H., J.G.K., J.L.B., M.W., M.B., G.R.V. and A.G.S. contributed to the acquisition of data. W.L., A.R.D., B.H. and J.G.K. contributed to the processing of data. W.L. developed the deep learning models. W.L., A.R.D., B.H., J.G.K., G.G., E.W., K.W., Y.B., M.B., G.R.V. and A.G.S. contributed to the analysis and interpretation of data. E.W. and J.O.O. developed the research computing infrastructure. W.L., A.R.D., E.W., K.W. and J.O.O. developed the evaluation code repository. W.L., A.R.D., B.H., J.G.K., G.G. and A.G.S. drafted the manuscript.
Corresponding authors
Ethics declarations
Competing interests
W.L., A.R.D., B.H., J.G.K., G.G., J.O.O., Y.B. and A.G.S. are employees of RadNet, the parent company of DeepHealth. M.B. serves as a consultant for DeepHealth. Two patent disclosures have been filed related to the study methods under inventor W.L.
Additional information
Peer review information Javier Carmona was the primary editor on this article, and managed its editorial process and peer review in collaboration with the rest of the editorial team.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Reader ROC curves using Probability of Malignancy metric.
For each lesion deemed suspicious enough to warrant recall, readers assigned a 0–100 probability of malignancy (POM) score. Cases not recalled were assigned a score of 0. a, ROC curve using POM on the 131 index cancer cases and 154 confirmed negatives. In order of reader number, the reader AUCs are 0.736 ± 0.023, 0.849 ± 0.022, 0.870 ± 0.021, 0.891 ± 0.019, and 0.817 ± 0.025. b, ROC curve using POM on the 120 pre-index cancer cases and 154 confirmed negatives. In order of reader number, the reader AUCs are 0.594 ± 0.021, 0.654 ± 0.031, 0.632 ± 0.030, 0.613 ± 0.033, and 0.694 ± 0.031. The standard deviation for each AUC value was calculated via bootstrapping.
Extended Data Fig. 2 Results of model compared to synthesized panel of readers.
Comparison of model ROC curves to every combination of 2, 3, 4 and 5 readers. Readers were combined by averaging BIRADS scores, with sensitivity and specificity calculated using a threshold of 3. On both the a, index cancer exams and b, pre-index cancer exams, the model outperformed every combination of readers, as indicated by each combination falling below the model’s respective ROC curve. The reader study dataset consists of 131 index cancer exams, 120 pre-index cancer exams and 154 confirmed negatives.
Extended Data Fig. 3 Comparison to recent work – index cancer exams.
The performance of the proposed model is compared to other recently published models on the set of index cancer exams and confirmed negatives from our reader study a-c, and the ‘Site A – DM dataset’ d. P-values for AUC differences were calculated using the DeLong method45 (two sided). Confidence intervals for AUC, sensitivity and specificity were computed via bootstrapping. a, ROC AUC comparison: Reader study data (Site D). The Site D dataset contains 131 index cancer exams and 154 confirmed negatives. The DeLong method z-values corresponding to the AUC differences are, from top to bottom, 3.44, 4.87, and 4.76. b, Sensitivity of models compared to readers. Sensitivity was obtained at the point on the ROC curve corresponding to the average reader specificity. Delta values show the difference between model sensitivity and average reader sensitivity and the P-values correspond to this difference (computed via bootstrapping). c, Specificity of models compared to readers. Specificity was obtained at the point on the ROC curve corresponding to the average reader sensitivity. Delta values show the difference between model specificity and average reader specificity and the P-values correspond to this difference (computed via bootstrapping). d, ROC AUC comparison: Site A – DM dataset. Compared to the original dataset, 60 negatives (0.78% of the negatives) were excluded from the comparison analysis because at least one of the models were unable to successfully process these studies. All positives were successfully processed by all models, resulting in 254 index cancer exams and 7,637 confirmed negatives for comparison. The DeLong method z-values corresponding to the AUC differences are, from top to bottom, 2.83, 2.08, and 14.6.
Extended Data Fig. 4 Comparison to recent work – pre-index cancer exams.
The performance of the proposed model is compared to other recently published models on the set of pre-index cancer exams and confirmed negatives from our reader study a-c, and the ‘Site A – DM dataset’ d. P-values for AUC differences were calculated using the DeLong method45 (two sided). Confidence intervals for AUC, sensitivity and specificity were computed via bootstrapping. a, ROC AUC comparison: Reader study data (Site D). The Site D dataset contains 120 pre-index cancer exams and 154 confirmed negatives. The DeLong method z-values corresponding to the AUC differences are, from top to bottom, 2.60, 2.66, and 2.06. b, Sensitivity of models compared to readers. Sensitivity was obtained at the point on the ROC curve corresponding to the average reader specificity. Delta values show the difference between model sensitivity and average reader sensitivity and the P-values correspond to this difference (computed via bootstrapping). c, Specificity of models compared to readers. Specificity was obtained at the point on the ROC curve corresponding to the average reader sensitivity. Delta values show the difference between model specificity and average reader specificity and the P-values correspond to this difference (computed via bootstrapping). d, ROC AUC comparison: Site A – DM dataset. Compared to the original dataset, 60 negatives (0.78% of the negatives) were excluded from the comparison analysis because at least one of the models were unable to successfully process these studies. All positives were successfully processed by all models, resulting in 217 pre-index cancer exams and 7,637 confirmed negatives for comparison. The DeLong method z-values corresponding to the AUC differences are, from top to bottom, 3.41, 2.47, and 6.81.
Extended Data Fig. 5 Localization-based sensitivity analysis.
In the main text, case-level results are reported. Here, we additionally consider lesion localization when computing sensitivity for the reader study. Localization-based sensitivity is computed at two levels – laterality and quadrant (see Methods). As in Fig. 2 in the main text, we report the model’s sensitivity at each reader’s specificity (96.1, 68.2, 69.5, 51.9, and 48.7 for Readers 1–5 respectively) and at the reader average specificity (66.9). a, Localization-based sensitivity for the index cases (131 cases). b, Localization-based sensitivity for the pre-index cases (120 cases). For reference, the case-level sensitivities are also provided. We find that the model outperforms the reader average for both localization levels and for both index and pre-index cases (*P < 0.05; Specific P-values: index – laterality: P < 1e − 4, index – quadrant: P = 0.01, pre-index – laterality: P = 0.01, pre-index – quadrant: P = 0.14). The results in the tables below correspond to restricting localization to the top scoring predicted lesion for both reader and model (see Methods). If we allow localization by any predicted lesion for readers while still restricting the model to only one predicted bounding box, the difference between the model and reader average performance is as follows (positive values indicate higher performance by model): index – laterality: 11.2 ± 2.8 (P = 0.0001), index – quadrant: 4.7 ± 3.3 (P = 0.08), pre-index – laterality: 7.8 ± 4.2 (P = 0.04), pre-index – quadrant: 2.3 ± 3.9 (P = 0.28). P-values and standard deviations were computed via bootstrapping. Finally, we note that while the localization-based sensitivities of the model may seem relatively low on the pre-index cases, the model is evaluated in a strict scenario of only allowing one box per study and crucially, all of the pre-index effectively represent ‘misses’ in the clinic. Even when set to a specificity of 90%36, the model still detects a meaningful number of the missed cancers while requiring localization, with a sensitivity of 37% and 28% for laterality and quadrant localization, respectively.
Extended Data Fig. 6 Reader study case characteristics and performance breakdown.
The performance of the proposed deep learning model compared to the reader average grouped by various case characteristics is shown. For sensitivity calculations, the score threshold for the model is chosen to match the reader average specificity. For specificity calculations, the score threshold for the model is chosen to match the reader average sensitivity. a, Sensitivity and model AUC grouped by cancer characteristics, including cancer type, cancer size and lesion type. The cases correspond to the index exams since the status of these features are unknown at the time of the pre-index exams. Lesion types are grouped by soft tissue lesions (masses, asymmetries and architectural distortions) and calcifications. Malignancies containing lesions of both types are included in both categories (9 total cases). ‘NA’ entries for model AUC standard deviation indicate that there were too few positive samples for bootstrap estimates. The 154 confirmed negatives in the reader study dataset were used for each AUC calculation. b, Sensitivity and model AUC by breast density. The breast density is obtained from the original radiology report for each case. c, Specificity by breast density. Confidence intervals and standard deviations were computed via bootstrapping.
Extended Data Fig. 7 Discrepancies between readers and the deep learning model.
For each case, the number of readers that correctly classified the case was calculated along with the number of times the deep learning model would classify the case correctly when setting a score threshold to correspond to either the specificity of each reader (for index and pre-index cases) or the sensitivity of each reader (for confirmed negative cases). Thus, for each case, 0–5 readers could be correct, and the model could achieve 0–5 correct predictions. The evaluation of the model at each of the operating points dictated by each reader was done to ensure a fair, controlled comparison (that is, when analyzing sensitivity, specificity is controlled and vice versa). We note that in practice a different operating point may be used. The examples shown illustrate discrepancies between model and human performance, with the row of dots below each case illustrating the number of correct predictions. Red boxes on the images indicate the model’s bounding box output. White arrows indicate the location of a malignant lesion. a, Examples of pre-index cases where the readers outperformed the model (i) and where the model outperformed the readers (ii). b, Examples of index cases where the readers outperformed the model (i) and where the model outperformed the readers (ii). c, Examples of confirmed negative cases where the readers outperformed the model (i) and where the model outperformed the readers (ii). For the example in c.i.), the patient previously had surgery six years ago for breast cancer at the location indicated by the model, but the displayed exam and the subsequent exam the following year were interpreted as BIRADS 2. For the example in c.ii.), there are posterior calcifications that had previously been biopsied with benign results, and all subsequent exams (including the one displayed) were interpreted as BIRADS 2. d, Full confusion matrix between the model and readers for pre-index cases. e, Full confusion matrix between the model and readers for index cases. f, Full confusion matrix between the model and readers for confirmed negative cases.
Extended Data Fig. 8 Performance of the proposed models under different case compositions.
Unless otherwise noted, in the main text we chose case compositions and definitions to match those of the reader study, specifically index cancer exams were mammograms acquired within 3 months preceding a cancer diagnosis and non-cancers were negative mammograms (BIRADS 1 or 2) that were ‘confirmed’ by a subsequent negative screen. Here, we additionally consider a, a 12-month definition of index cancers, meaning mammograms acquired within 0–12 months preceding a cancer diagnosis, as well as b, including biopsy-proven benign cases as non-cancers. The 3-month time window for cancer diagnosis includes 1,205, 533, 254 and 78 cancer cases for OMI-DB, Site E, Site A – DM, and Site A – DBT, respectively. The number of additional cancer cases included in the 12-month time window is 38, 46 and 7 for OMI-DB, Site A – DM, and Site A – DBT, respectively. A 12–24 month time window results in 68 cancer cases for OMI-DB and 217 cancer cases for Site A – DM. When including benign cases, those in which the patient was recalled and ultimately biopsied with benign results, we use a 10:1 negative to benign ratio to correspond with a typical recall rate in the United States.36 For a given dataset, the negative cases are shared amongst all cancer time window calculations, with 1,538, 1,000, 7,697 and 518 negative cases for OMI-DB, Site E, Site A – DM, and Site A – DBT, respectively. For all datasets except Site E, the calculations below involve confirmed negatives. Dashes indicate calculations that are not possible given the data and information available for each site. The standard deviation for each AUC value was calculated via bootstrapping.
Extended Data Fig. 9 Aggregate summary of testing data and results.
Results are calculated using index cancer exams and both confirmed negatives and all negatives (confirmed and unconfirmed) separately. While requiring negative confirmation excludes some data, similar levels of performance are observed across both confirmation statuses in each dataset. Across datasets, performance is also relatively consistent, though there is some variation as might be expected given different screening paradigms and population characteristics. Further understanding of performance characteristics across these populations and other large-scale cohorts will be important future work. The standard deviation for each AUC value was calculated via bootstrapping.
Extended Data Fig. 10 Examples of maximum suspicion projection (MSP) images.
Two cancer cases are presented. Left column: Default 2D synthetic images. Right column: MSP images. The insets highlight the malignant lesion. In both cases, the deep learning algorithm scored the MSP image higher for the likelihood of cancer (a: 0.77 vs. 0.14, b: 0.87 vs. 0.31). We note that the deep learning algorithm correctly localized the lesion in both of the MSP images as well.
Supplementary information
Rights and permissions
About this article
Cite this article
Lotter, W., Diab, A.R., Haslam, B. et al. Robust breast cancer detection in mammography and digital breast tomosynthesis using an annotation-efficient deep learning approach. Nat Med 27, 244–249 (2021). https://doi.org/10.1038/s41591-020-01174-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41591-020-01174-9
This article is cited by
-
Segmentation for mammography classification utilizing deep convolutional neural network
BMC Medical Imaging (2024)
-
Pathogenomics for accurate diagnosis, treatment, prognosis of oncology: a cutting edge overview
Journal of Translational Medicine (2024)
-
Artificial intelligence as an initial reader for double reading in breast cancer screening: a prospective initial study of 32,822 mammograms of the Egyptian population
Egyptian Journal of Radiology and Nuclear Medicine (2024)
-
Diagnosis model of early Pneumocystis jirovecii pneumonia based on convolutional neural network: a comparison with traditional PCR diagnostic method
BMC Pulmonary Medicine (2024)
-
Spatial and geometric learning for classification of breast tumors from multi-center ultrasound images: a hybrid learning approach
BMC Medical Imaging (2024)