Introduction

Entropy production, a fundamental concept in nonequilibrium thermodynamics, provides a measure of the degree of irreversibility of a physical process. It is of paramount importance for the characterization of an ample range of systems across all scales, from macroscopic to microscopic1,2,3,4,5,6,7,8,9,10,11. The lack of a continuity equation for entropy prevents entropy production from being a physical observable, in general. Its quantification must thus pass through inference strategies that connect the values taken by such quantity to accessible observables, such as energy12,13,14. This approach has recently led to the possibility to experimentally measure entropy production in microscopic15 and mesoscopic quantum systems16, and opened up intriguing opportunities for its control17. Alternative approaches to the quantification of entropy production are based on the ratio between forward and time-reversed path probabilities of trajectories followed by systems undergoing nonequilibrium processes18,19,20.

A large body of work has been produced in an attempt to overcome the lack of generally applicable theories of entropy production11,21. Remarkably, this has allowed the identification of important contributions to the irreversibility emerging from a given process stemming from system–environment correlations17,22,23, quantum coherence24,25,26, and the finite size of the environment23,27.

Among the directions of potential further investigations, a particularly relevant one is the inclusion of the back action, resulting from measuring a quantum system. Measurements can have a dramatic effect on both the state and the ensuing dynamics of a quantum system: while the randomness brought about by a quantum measurement adds stochasticity to the evolution of a system, the information gained through a measurement process unlocks effects akin to those of a Maxwell daemon28,29. Both such features are intuitively expected to affect the entropy production and its rate (cf. Fig. 1).

Fig. 1: Scheme of principle.
figure 1

a A system, prepared in an arbitrary state and being externally driven, interacts with an environment. The dynamics is associated with a (unconditional) rate of entropy production Πuc. b Continuous measurements alter the dynamics of the system, resulting in an entropy production rate Π that includes an information-theoretical contribution \(\dot{{\mathcal{I}}}\) determined by the amount of information extracted through the measurement.

Full size image

The ways such modifications occur have been the focus of some attention recently. Elouard et al. and Manikandan et al.29,30 tackled the problem by focusing on the stochastic energy fluctuations that occur during measurements, while refs. 31,32,33,34,35,36,37,38,39 addressed the case of weak quantum measurements of a system, which allowed for the introduction of trajectory-dependent work and heat quantifiers (cf. refs. 40,41). In line with a Landauer-like framework, Sagawa and Ueda focused on the minimum thermodynamic cost implied by a measurement, highlighting the information theoretical implications of the latter on the stochastic thermodynamics of a two-level system42,43, an approach that can both be generalized to general quantum measurements44 and assessed experimentally45.

Here, we contribute to the quest for a general framework for entropy production and its rate in a general system brought out of equilibrium and being continuously monitored. We propose a widely applicable formalism able to identify the measurement-affected rate of entropy production, and the associated entropy flux to or from the environment that is connected to the monitored system. We unveil the thermodynamic consequences of measuring by way of both general arguments and specific case studies, showing that the entropy production rate can be split in a term that is intrinsically dynamical and one that is informational in nature. We show that, for continuously measured Gaussian systems, the entropy production splitting leads to a refined, tighter second law. We also discuss the possibility to control the nonequilibrium thermodynamics of a system through suitable measurements. We illustrate it by studying a thermal quench of an harmonic oscillator and a driven dissipative optical parametric oscillator.

Our approach paves the way to the assessment of the nonequilibrium thermodynamics of continuously monitored Gaussian systems—such as (ensembles of) trapped ions and quadratically confined levitated optomechanical systems—whose energetics will require tools designed to tackle the intricacies of quantum dynamics and the stochasticity of quantum measurements, which are currently lacking46,47,48,49,50,51,52,53,54,55.

Results

Entropy rate of a continuously measured system

The dynamics of a continuously measured Markovian open quantum system can be described by a stochastic master equation (SME) that describes the evolution conditioned on the outcomes of the continuous measurement56,57,58. Upon averaging over all trajectories, weighted by the outcomes probabilities, the stochastic part vanishes leaving a deterministic Lindblad ME for the system, whose dynamics we call unconditional.

In the unconditional case, the entropy rate can be split as \({\dot{S}}_{{\rm{uc}}}={\Phi }_{{\rm{uc}}}+{\Pi }_{{\rm{uc}}}\) with Φuc (Πuc) the unconditional entropy flux (production) rate11, with Suc an entropic measure. The second law of thermodynamics for the unconditional dynamics is encoded in Πuc ≥ 0. It should be noted that, choosing the widely used von Neumann entropy leads to controversial results, when the system is in contact with a vanishing-temperature thermal bath59,60. We will address this point again later on.

For the conditional dynamics, a similar splitting of the entropy rate can be obtained, although involving stochastic trajectory-dependent quantities. Indeed, given that the conditional dynamics describes quantum trajectories in Hilbert space, the entropy rate and the entropy production are stochastic quantities. We are interested in the average of such stochastic quantities over all trajectories, i.e.,

$${\mathbb{E}}[{\mathrm{d}}S/{\mathrm{d}}t]={\mathbb{E}}\left[{\mathrm{d}}\phi /{\mathrm{d}}t\right]+{\mathbb{E}}\left[{\mathrm{d}}\pi /{\mathrm{d}}t\right]=\Phi +\Pi ,$$
(1)

where dS, dπ, and dϕ depend on the stochastic conditional state, and Π and Φ are the averaged conditional entropy production and flux rates. These quantities will in general differ from their unconditional counterparts because they depend nonlinearly on the state of the system. We now move on to explain in more detail their physical interpretation.

Operationally, the conditional dynamics is obtained by continuously monitoring the system and recording the outcomes of the measurement. After repeating the experiments many times, and computing each time the stochastic entropy flux and entropy production rate, one finally averages these quantities over the stochastic trajectories of the system. Such average quantities are related to the state of the system conditioned on the outcomes of the continuous measurements. On the contrary, the unconditional dynamics is recovered by ignoring the outcomes of the measurements at the level of the state of the system. Thus, the state of the system, from which the statistics are inferred, corresponds to the average over the possible outcomes of the conditional state at each instant of time.

We aim to connect Π to the entropy produced by the system due to only the open system dynamics (Πuc). We thus assume that the stochastic entropy flux is linear in the conditioned state of the system, i.e., \({\Bbb{E}}[{\mathrm{d}}\phi /{\mathrm{d}}t]={\Phi }_{{\rm{uc}}}\). This is so in all those cases where the entropy flux is given by the heat flux from the system to an (equilibrium) environment at a reference temperature, a second relevant instance being when the entropy flux is associated to the occurrence of a quantum jump of the system8. To the best of our knowledge, no example of violation of this assumption has been reported in the literature so far. However, a formal proof of linearity is still missing. As we aim at a general framework that encompasses nonequilibrium states of the environment, here we do not necessarily identify the entropy flux rate with the heat flow rate to a thermal environment, while claiming for its linearity in the conditional state of the system. In what follows we show that, for Gaussian systems, this linearity can be explicitly proven. The same can be done for more general systems starting from a microscopic description of the system–environment interaction via a repeated collisions model61.

By comparing the splitting of the entropy rate for conditioned and unconditioned dynamics, we arrive at

$$\Pi ={\Pi }_{{\rm{uc}}}+\dot{{\mathcal{I}}},$$
(2)

where the last term quantifies the entropic cost of continuously monitoring the system and, as Φ = Φuc, it must then follow \(\dot{{\mathcal{I}}}={\mathbb{E}}[{\mathrm{d}}S/{\mathrm{d}}t]-{\mathrm{d}}{S}_{{\rm{uc}}}/{\mathrm{d}}t\).

In order to further characterize the informational term \(\dot{{\mathcal{I}}}\) and, in particular, single out the entropy production and flux rates, we focus on open Gaussian systems subject to continuous Gaussian measurements. Such a class of systems and processes plays a substantive role in the broad panorama of quantum optics, condensed matter physics, and quantum information science in general. Gaussian measurements are some of the most widely used techniques in quantum labs, and their role in stochastic nonclassical thermodynamics is thus both interesting and physically very well motivated.

The Gaussian case calls for the use of powerful phase-space techniques, in conjunction with the adoption of the Wigner entropy as an entropic measure59, which allow us to unambiguously identify the entropy flux and production rates based on the dynamics of the system, without resorting to a thermal environment (at finite temperature) and bypasses some of the controversies linked to more standard von Neumann entropy-based formulations59, thus going beyond any standard approach. It should be noted that, in some cases of continuously measured quantum Gaussian systems, e.g., homodyne detection of an optical mode, where the bath mode being monitored is effectively at zero temperature, there are no alternatives to the adoption of the Wigner entropy due to the unphysical divergences that plague the definition of entropy production and fluxes obtained by adopting the von Neumann entropy59,60. Nonetheless, consistently with classical stochastic thermodynamics, ref. 59 showed that the results obtained using the Wigner entropy agree with the von Neumann ones, and crucially with the classical ones, for systems interacting with thermal baths in the high-temperature limit. Finally, we would like to remark that refs. 62,63 made a step forward to extend phase-space-based formulation of entropy production rate and flux to the case of non-Gaussian systems and dynamics, using the well-known Wehrl entropy defined in terms of the Shannon entropy of the Husimi function. All the considerations reported here can be generalized straightforwardly to the use of the Wehrl entropy.

Continuously measured Gaussian systems

Solving the SME is in general a tall order. Luckily, the intricacy of such an approach is greatly simplified when dealing with Gaussian systems, as their description can be reduced to the knowledge of the first two statistical moments of the quadratures of the system. The SME can thus be superseded by a simpler system of stochastic equations. We consider a system of n modes, each described by quadrature operators \(({\hat{q}}_{i},{\hat{p}}_{i})\) with \([{\hat{q}}_{j},{\hat{p}}_{j}]=i\), and define the vector \(\hat{{\bf{x}}}=({\hat{q}}_{1},{\hat{p}}_{1},{\hat{q}}_{2},{\hat{p}}_{2},\ldots ,{\hat{q}}_{n},{\hat{p}}_{n})\). When restricting to Gaussian systems, the Hamiltonian is at most quadratic in the quadrature operators and can be written as \(\hat{H}=\frac{1}{2}{\hat{{\bf{x}}}}^{{\mathrm{T}}}{H}_{s}\hat{{\bf{x}}}+{{\bf{b}}}^{{\mathrm{T}}}\Omega \hat{{\bf{x}}}\), where Hs is a 2n × 2n matrix, b is a 2n-dimensional vector accounting for a (time-dependent) linear driving, and \(\Omega ={\oplus }_{j = 1}^{n}i{\sigma }_{y,j}\) is the n-mode symplectic matrix (σy,j is the y-Pauli matrix of subsystem j). For an environment modeled by Lindblad generators that are linear in the quadratures of the system and the latter is monitored through Gaussian measurements, the dynamics preserves the Gaussianity of any initial state. In this case, the vector of average moments \(\bar{{\bf{x}}}=\langle \hat{{\bf{x}}}\rangle\) and the covariance matrix (CM) \({\sigma }_{ij}=\langle \{{\hat{{\bf{x}}}}_{i},{\hat{{\bf{x}}}}_{j}\}\rangle /2-\langle {\hat{{\bf{x}}}}_{i}\rangle \langle {\hat{{\bf{x}}}}_{j}\rangle\) of the modes completely describe the dynamics via the equations57,58,64

$$\begin{array}{*{20}{l}}\dot{\sigma }=A\sigma +\sigma {A}^{{\mathrm{T}}}+D-\chi (\sigma ),\\ {\mathrm{d}}\bar{{\bf{x}}}=(A\bar{{\bf{x}}}+{\bf{b}}){\mathrm{d}}t+(\sigma {C}^{{\mathrm{T}}}+{\Gamma }^{{\mathrm{T}}}){\mathrm{d}}{\bf{w}},\end{array}$$
(3)

where dw is a 2ℓ-dimensional vector of Wiener increments (ℓ is the number of output degrees of freedom being monitored), A(D) is the drift (diffusion) matrix characterizing the unconditional open dynamics of the system, and χ(σ) = (σCT + ΓT)(Cσ + Γ) ≥ 0 is defined in terms of the 2ℓ × 2n matrices C and Γ that describe the measurement process (see ref. 57 and references therein for a detailed derivation of these equations). While the explicit form of such matrices is inessential for our scopes (cf. refs. 57,58,64), we highlight the fact that the drift matrix A can be decomposed as A = ΩHs + Airr, where the first term accounts for the unitary evolution and the second for diffusion. Notwithstanding the stochasticity of the overall dynamics, the equation for the CM is deterministic. Thus, σ(t) does not depend on the explicit outcomes of the measurement (i.e., the trajectory followed by the system), while it depends on the measurement carried out58. The dynamics of the corresponding unconditional quantities σuc and \({\bar{{\bf{x}}}}_{{\rm{uc}}}\) is achieved from Eq. (3) by taking \(C=\Gamma ={\Bbb{O}}\) with \({\Bbb{O}}\) the null 2ℓ × 2n matrix. This then implies χ(σ) = 0, so that one recovers the dynamical equation for the evolution of σuc.

Entropy production rate and flux

Equation (3) can be conveniently cast in the phase space as the continuity equation (cf. Supplementary Information)

$${\mathrm{d}}W=-{\rm{div}}[J{\mathrm{d}}t+{J}_{{\rm{sto}}}],$$
(4)

where \(W={e}^{-\frac{1}{2}{({\bf{x}}-\bar{{\bf{x}}})}^{{\mathrm{T}}}{\sigma }^{-1}({\bf{x}}-\bar{{\bf{x}}})}/{(2\pi )}^{n}\sqrt{\det \sigma }\) is the Wigner function associated with the state of the n-mode system and we have introduced the deterministic phase-space current J, which can be divided as J = Jrev + Jirr, and its stochastic counterpart Jsto. Here, Jrev = ΩHsxW + bW encodes the contribution stemming from the unitary dynamics and Jirr = AirrxW − (D/2)∇W accounts for the irreversible dissipative evolution. It should be noted that these currents are equal to the ones of the unconditional dynamics with the replacement W → Wuc, where Wuc is the Wigner function of the unconditional state obtained through the replacements σ → σuc and \(\bar{{\bf{x}}}\to {\bar{{\bf{x}}}}_{{\rm{uc}}}\). The stochastic term Jsto = W(σCT + ΓT)dw depends entirely on the conditional dynamics, through σ and W, and the measurement strategy being chosen.

In order to characterize the entropy of the n-mode system, we adopt the Wigner entropy \(S=-\int W\mathrm{ln}\,W\ {{\mathrm{d}}}^{2n}{\bf{x}}\) as our entropic measure. For Gaussian systems65

$$S=\frac{1}{2}{\mathrm{ln}}\,(\det \sigma )+{k}_{n}=-{\mathrm{ln}}\,({\mathcal{P}})+{\tilde{k}_{n}},$$
(5)

with \({k}_{n},{\tilde{k}}_{n}\) inessential constants that depends only on the number n of modes involved and \({\mathcal{P}}\) the purity of the state of the system, which for a Gaussian state reads \({\mathcal{P}}={(\det 2\sigma )}^{-1/2}\). This also coincides with the Rényi-2 entropy65 and tends to the von Neumann entropy in the classical limit of high temperatures. Let us note that the Renyi-α entropy for a generic N-mode Gaussian state is defined as \({S}_{\alpha }(\rho )=\frac{1}{\alpha -1}\mathop{\sum }\nolimits_{i = 1}^{N}\mathrm{ln}\,{f}_{\alpha }({\sigma }_{i})\), where \({f}_{\alpha }({\sigma }_{i})={\left(\frac{{\sigma }_{i}+1}{2}\right)}^{\alpha }-{\left(\frac{{\sigma }_{i}-1}{2}\right)}^{\alpha }\) and σi is the ith symplectic eigenvalues of the Gaussian state. A “classical limit” for such a quantity can be recovered by considering σi ≫ 1, i.e., the “high-temperature limit”. In these conditions, it is easy to see that the Rényi-α entropy reduces to \({S}_{\alpha }(\rho )=N\mathrm{log}\,\alpha /(\alpha -1)-N\mathrm{log}\,2+\mathop{\sum }\nolimits_{i = 1}^{N}\mathrm{log}\,{\sigma }_{i}\). We see that, except for a α-dependent constant, this matches the von Neumann entropy.

As the Wigner entropy only depends on the CM of the system, its evolution is deterministic even for continuously measured system, a peculiarity of Gaussian systems. The same then holds true for the entropy rate given by

$$\frac{{\mathrm{d}}S}{{\mathrm{d}}t}=\frac{1}{2}\frac{d}{{\mathrm{d}}t}({\rm{Tr}}[\mathrm{log}\,\sigma ])=\frac{1}{2}{\rm{Tr}}[2A+{\sigma }^{-1}(D-\chi (\sigma ))].$$
(6)

In the unconditional case, the entropy rate is \({\dot{S}}_{{\rm{uc}}}={\Phi }_{{\rm{uc}}}+{\Pi }_{{\rm{uc}}}\)11, and both the unconditional entropy flux and production rates depend on the irreversible part of the phase-space current Jirr. In the Supplementary Information accompanying this paper, we report expressions for these quantities written in terms of Airr, σuc, and D. For a system interacting with a high-temperature thermal environment, Φuc coincides with the energy flux from the system to the environment. Thus, this formalism generalizes the usual thermodynamic description in a meaningful manner.

For the continuously measured case, while Eq. (6) presents a deterministic quantity, both the entropy flux and production rate are inherently stochastic, as they depend on the first moments of the quadrature operators. Nonetheless, using Eq. (4), it is possible to single out the entropy production and flux rates as the quadratic and linear part of dS/dt in the irreversible currents, respectively. The entropy rate is thus written as \({\mathrm{d}}S={\mathrm{d}}{\phi }_{\bar{{\bf{x}}}}+{\mathrm{d}}{\pi }_{\bar{{\bf{x}}}}\) with \({\mathrm{d}}{\phi }_{\bar{{\bf{x}}}},\ {\mathrm{d}}{\pi }_{\bar{{\bf{x}}}}\) the conditioned trajectory-dependent entropy flux and production rates. It can be shown that, upon taking the average (\({\Bbb{E}}\)) over the outcomes of the measurements, \({\Bbb{E}}\left[{\mathrm{d}}{\phi }_{\bar{{\bf{x}}}}/{\mathrm{d}}t\right]={\Phi }_{{\rm{uc}}}\), demonstrating that the linearity of the stochastic entropy flux in the state of the system is a property of Gaussian systems and does not need to be postulated, as shown in the Supplementary Information. Thus, on average, we can rewrite the entropy as \(\dot{S}={\Bbb{E}}\left[{\mathrm{d}}{\phi }_{\bar{{\bf{x}}}}/{\mathrm{d}}t\right]+{\Bbb{E}}\left[{\mathrm{d}}{\pi }_{\bar{{\bf{x}}}}/{\mathrm{d}}t\right]={\Phi }_{{\rm{uc}}}+\Pi\).

As the entropy of the conditioned system is deterministic, we can write \(\dot{S}={\dot{S}}_{{\rm{u}}c}+\dot{{\mathcal{I}}}\), where the term \(\dot{{\mathcal{I}}}\) accounts for the excess entropy production, resulting from the measurement process. Indeed, by integrating the above expression, one finds \({\mathcal{I}}=\mathrm{ln}\,({{\mathcal{P}}}_{{\rm{uc}}}/{\mathcal{P}})\), showing that \({\mathcal{I}}\) quantifies the noise to be added to the conditional state to bring it back to its unconditional form. As, in general, we have \({\mathcal{P}}\ge {{\mathcal{P}}}_{{\rm{uc}}}\), we gather that \({\mathcal{I}}\le 0\). In fact, it can be further shown that \({\mathcal{I}}=-I({\bf{X}}:\bar{{\bf{X}}})\le 0,\) with I the classical mutual information between the phase-space position X in the unconditional case and the stochastic first moments \(\bar{{\bf{X}}}\), which evolve according to the Itô equation in Eq. (3). The inequality is saturated iff σ = σuc (see Supplementary Information for details). A straightforward calculation based on Eq. (6) leads to

$$\dot{{\mathcal{I}}}=\frac{1}{2}{\rm{Tr}}[{\sigma }^{-1}(D-\chi (\sigma ))-{\sigma }_{{\rm{uc}}}^{-1}D],$$
(7)

where, as seen from Eq. (3), D − χ(σ) accounts for a modification to the diffusion matrix of the dynamics occurring due to the choice of measurement: the latter conjures with the environment and acts on the system so as to modify its diffusive dynamics. Equation (7) embodies the effects of continuous detection, which modifies the CM of the system and its dynamics.

As for Eq. (2), we have \(\Pi ={\Pi }_{{\rm{uc}}}+\dot{{\mathcal{I}}}.\) This is the main result of this work. It connects the entropy production rate of the unmonitored open Gaussian system to the homonymous quantity for the monitored one via the informational term \(\dot{{\mathcal{I}}}\). The second law for the unmonitored system Πuc ≥ 0 can now be used to obtain the refined second law for continuously measured Gaussian systems \(\Pi \ge \dot{{\mathcal{I}}}\), which epitomizes the connection between nonequilibrium thermodynamics and information theory, as pioneered by Landauer’s principle. The degree of irreversibility of the dynamics being considered, which is associated with a change in entropy of the state of the system, is lower-bounded by an information theoretical cost rate that depends on the chosen measurement, and that is in general more stringent than that associated with the unmeasured dynamics. This echoes and extends significantly the results in ref. 43, which were valid for discrete measurements and equilibrium environments.

Case study

To illustrate our framework, we consider two relevant examples: a thermal quench and the driven dissipative optical parametric oscillator. In both cases, the system (either a driven harmonic oscillator or an optical parametric oscillator) is monitored by a single field mode in thermal equilibrium. We call \({\bar{n}}\)th the mean occupation number of such thermal state of the field, which is subjected to general-dyne measurements57. The system is coupled to the thermal field mode via an excitation–exchange interaction,

$${\hat{H}}_{{\mathrm{int}}}=\sqrt{\gamma }{\hat{{\bf{x}}}}^{{\mathrm{T}}}{\hat{{\bf{x}}}}_{B},$$
(8)

where \(\hat{{\bf{x}}}=(\hat{q},\hat{p})\) and \({\hat{{\bf{x}}}}_{B}\) represent the quadratures vector for system and bath, respectively. Calling Hs the system Hamiltonian in the two cases, the SME describing the conditional dynamics of the continuously monitored system is written as57

$$\dot{\rho }=-i[{H}_{s},\rho ]+\gamma ({\bar{n}}_{{\rm{th}}}+1){\mathcal{D}}[\hat{a}]\rho +{\gamma {\bar{n}}_{{\rm{th}}}}{\mathcal{D}}[{\hat{a}}^{\dagger }]\rho +\sqrt{\gamma }{\mathcal{H}}[\hat{a}]\rho dw,$$
(9)

where \({\mathcal{D}}[\hat{{\mathcal{O}}}]\rho =\hat{{\mathcal{O}}}\rho {\hat{{\mathcal{O}}}}^{\dagger }-({\hat{{\mathcal{O}}}}^{\dagger }\hat{{\mathcal{O}}}\rho +\rho {\hat{{\mathcal{O}}}}^{\dagger }\hat{{\mathcal{O}}})/2\), dw is a Wiener increment, and \({\mathcal{H}}[\hat{{\mathcal{O}}}]\rho =\hat{{\mathcal{O}}}\rho +\rho {\hat{{\mathcal{O}}}}^{\dagger }-{\rm{Tr}}[\rho (\hat{{\mathcal{O}}}+{\hat{{\mathcal{O}}}}^{\dagger })]\rho\). The last, stochastic term in Eq. (9) encodes the effect of the continuous monitoring of the \(\hat{p}\) quadrature of the environment’s mode (cf. ref. 58). Similar SMEs describe general-dyne measurements (cf. refs. 64,66,67 for the most general SME for bosonic systems and Markovian dynamics, and further details).

The two exemplary cases that we consider are (I) a driven harmonic oscillator described by \({H}_{s}=\omega /2\ ({\hat{q}}^{2}+{\hat{p}}^{2})+{H}_{{\mathrm{drive}}}\), where \({H}_{{\mathrm{drive}}}=i{\mathcal{E}}(\hat{a}{e}^{i\theta }-{\hat{a}}^{\dagger }{e}^{-i\theta })\) describes the driving by a pump of amplitude \({\mathcal{E}}\) and phase θ; (II) the optical parametric oscillator described by \({H}_{s}=-\chi /2\ (\hat{q}\hat{p}+\hat{p}\hat{q})\). From now on we work in natural units and set ω = χ = 1. Further details on these examples and their description in the Gaussian framework can be found in the “Methods” section.

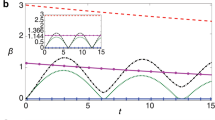
In Fig. 2, the behavior of the entropy production rate, entropy flux rate, and \(\dot{{\mathcal{I}}}\) is shown for both systems under either homodyne or heterodyne measurements. For example (I), we have chosen a thermal bath with \(2{\bar{n}}\)th + 1 = 100 and a displaced thermal initial state for the system with a larger initial temperature. The system is thus cooled down by the interaction with the environment. For the parametric oscillator in example (II), the thermal bath is chosen at zero temperature, the initial state is a squeezed vacuum state, and we also consider a small additive Gaussian noise so as to make the detection not ideal. Such additional noise makes the steady state different for different detection strategies.

Fig. 2: Numerical example.
figure 2

a–c Thermal quench of a harmonic oscillator interacting with an environment in thermal equilibrium (mean occupation number \({\bar{n}}\)th such that \(2{\bar{n}}\)th + 1 = 100) and subjected to homodyne and heterodyne measurements. The initial state of the harmonic oscillator, which is externally driven by a pump of amplitude \({\mathcal{E}}\), is thermal with an energy ten times larger than the environment. a, b Πuc (dashed blue curve), Π (solid red curve), Φ (black dotted curve), and \(\dot{{\mathcal{I}}}\) (dot-dashed green curve) for homodyne (monitoring of the system’s momentum quadrature) and heterodyne detection. c \({\mathcal{I}}\) when homodyning the position and momentum quadratures of the system (dot-dashed green curve and dotted red curve, respectively), and heterodyne measurements (dashed blue curve). d–f Optical parametric oscillator in contact with an external mode in thermal equilibrium (\({\bar{n}}\)th = 0), and subjected to homodyne and heterodyne measurements with additional Gaussian noise. d and e are analogous to a and b. f \({\mathcal{I}}\) for various detection schemes (cf. “Methods” section).

Full size image

The behavior of the information rate \(\dot{{\mathcal{I}}}\) in both examples is consistent with expectations (cf. Fig. 2a, b, d, e). It starts at an initially large negative value in light of the nonequilibrium nature of the initial state, but then vanishes as the system approaches the steady state of the conditional dynamics. In fact, at the steady state no additional information on the system is acquired with respect to the one acquired up to that moment. This does not mean, however, that the continuous measurement is unnecessary at the steady state. Indeed, the continuous monitoring sustains the steady state, which would otherwise evolve toward its unconditional counterpart effectively causing a loss of information61,68.

It should be noted that, after an initial negative phase, \(\dot{{\mathcal{I}}}\) becomes positive in both examples, consistently with Fig. 2c–f. While \(\dot{{\mathcal{I}}}\) takes both positive and negative values, the regions where \(\dot{{\mathcal{I}}}\,>\,0\) show how our refined second law offers a more stringent constraint than the standard one.

Finally, by comparing Fig. 2c, f, we note a stark qualitative difference between the informational terms resulting from the dynamics of a harmonic oscillator subjected to a thermal quench and the optical parametric oscillator. Indeed, the inspection of the results for the thermal quench shows that \({\mathcal{I}}\to 0\) at the steady state (cf. Fig. 2c). This is justified by the fact that the steady state of the conditional and unconditional dynamics is the same irrespective of the measurement, and asymptotically no extra information from the measurements is acquired with respect to the unconditional case. In contrast, Fig. 2f, which refers to the parametric oscillator, shows different long-time behavior of \({\mathcal{I}}\) for different measurements due to the additive Gaussian noise that is introduced by the choice of detection strategy. This makes the steady state of the conditioned dynamics mixed, with a purity dependent on the measurement and, in turn, the measurement outcomes remain informative also in the asymptotic regime.

Discussion

We have characterized the entropy production rate of continuously monitored nonequilibrium Gaussian quantum processes in terms of the effects induced by measurement. This led us to the formulation of a refined second law reminiscent of Landauer’s principle, and in line with previous results valid for discrete measurements and systems. However, it should be noted that, the particular form of this refined second law is tailored to Gaussian dynamics and the Wigner entropy as an entropic measure.

On one hand, our results shine light on the emerging field of information thermodynamics, highlighting the tight fundamental link between nonequilibrium thermodynamics and information gains. On the other hand, they offer a general way to define the entropy production and flux rates for Gaussian systems, thus overcoming the limitations of previous approaches.

Our framework will be invaluable to analyze and characterize the nonequilibrium dynamics of experimental systems of strong current interest. In particular, levitated quantum optomechanics offers fertile ground for the application of our formalism48,49,51,52,53,54,55,68.

Methods

Here, we give some additional specifics of the two examples considered in the main text, i.e., the thermal quench of a simple harmonic oscillator and the optical parametric oscillator coupled to a thermal bath. In doing so, we follow closely58 where the example of the optical parametric oscillator is described in details. The bath is described, in both our examples, by the initial single mode CM \({{\sigma }_{B}=({{n}_{{\rm{th}}}}+1/2){\mathbb{I}}}\). The excitation–exchange interaction Hamiltonian, also common to both the examples, is given by

$${\hat{H}}_{{\mathrm{int}}}=\sqrt{\gamma }{\hat{{\bf{x}}}}^{{\mathrm{T}}}{\hat{{\bf{x}}}}_{B}=\frac{1}{2}(\hat{{\bf{x}}},{\hat{{\bf{x}}}}_{B})\left(\begin{array}{*{20}{l}}0&{\mathcal{C}}\\ &\\ {\mathcal{C}}&0\\ \end{array}\right)\left(\begin{array}{*{20}{l}}\hat{{\bf{x}}}\\ {\hat{{\bf{x}}}}_{B}\end{array}\right),\ \ \ {\mathcal{C}}=\left(\begin{array}{*{20}{l}}\sqrt{\gamma }&0\\ 0&\sqrt{\gamma }\end{array}\right),$$
(10)

where we have introduced the quadratures of the bath \({\hat{{\bf{x}}}}_{B}\). A general-dyne, noisy measurement is described, in the Gaussian formalism, by giving the CM corresponding to the state over which one project. For an ideal general-dyne measurement on the single output mode, the state is pure and the CM is given by the 2 × 2 matrix

$$2{\sigma }_{m}=R{[\varphi ]}^{{\mathrm{T}}}\left({\begin{array}{ll}s&0\\ 0&1/s\end{array}}\right)R[\varphi ],$$
(11)

where R[φ] is a rotation matrix and s > 0. Note that, given the form of the excitation–exchange interaction Hamiltonian, s = 0 corresponds to homodyne detection of the x—quadrature of the output mode, and thus the indirect monitoring of the p—quadrature of the system, s = 1 corresponds to heterodyne detection on the output mode, and s = ∞ to indirect monitoring of the x—quadrature of the system (homodyne detection of the p—quadrature of the output mode). In order to account for noisy measurements, the CM σm needs to be modified by acting on it with the dual of a CP Gaussian map. The reason for this stems from the fact that a noisy measurement can be seen as the action of a CP Gaussian map on the state of the system previous to an ideal general-dyne measurement58. For our simple case, the CM σm for a general-dyne detection with efficiency η ∈ [0, 1] and additive Gaussian noise Δ is given by

$$2\sigma_{m} = R{[\varphi]}^{{\mathrm{T}}} \left(\begin{array}{*{20}{l}}s/\eta & 0\\ 0 & 1/(s\eta)\end{array}\right)R[\varphi]+\left(\begin{array}{*{20}{l}}(1-\eta)/\eta+\Delta & 0\\ 0 & (1-\eta)/\eta+\Delta\end{array}\right).$$
(12)

Given the measurement CM and the interaction Hamiltonian, we can obtain the measurements matrices Γ, C. For both our examples, these are given by

$${\Gamma }^{{\mathrm{T}}}=\frac{1}{\sqrt{2}}\Omega {\mathcal{C}}{\sigma }_{B}{\left({\sigma }_{B}+{\sigma }_{m}\right)}^{-1/2},$$
(13)
$${C}^{{\mathrm{T}}}=-\sqrt{2}{\mathcal{C}}\Omega {\left({\sigma }_{B}+{\sigma }_{m}\right)}^{-1/2}.$$
(14)

It should be noted that, in the limit of η → 0 and/or Δ → ∞, i.e., for zero efficiency of the detectors and/or infinite additive Gaussian noise, the conditional dynamics converges to the unconditional one. This is intuitive, given that in both these situations no information about the system is acquired by the inefficient/very noisy detection scheme. However, this highlight also another interesting aspect of this type of noisy general-dyne detection: no matter how large the additive noise or how inefficient the detectors, the conditional dynamics will never increase the uncertainty on the state of the system more than the unconditional dynamics.

Finally, we specify the Hamiltonians of the two systems that we consider and we explicit the parameters chosen in Fig. 2. For the thermal quench of the harmonic oscillator, we chose a thermal occupation number of the bath such that 2nth + 1 = 100. The Hamiltonian of the system, comprising a quadratic term and a linear drive, is given by

$${\hat{H}}_{s}=\frac{1}{2}{\hat{{\bf{x}}}}^{{\mathrm{T}}}\left(\begin{array}{*{20}{l}}\omega &0\\ 0&\omega \end{array}\right)\hat{{\bf{x}}}+{{\boldsymbol{d}}}^{{\mathrm{T}}}\Omega \hat{{\bf{x}}},$$
(15)

where \(d=-(\sqrt{2}{\mathcal{E}}\cos \theta ,\sqrt{2}{\mathcal{E}}\sin \theta )\) and the driving term correspond, in terms of annihilation and creation operators of the system oscillator, to \({\hat{H}}_{{\rm{drive}}}=i{\mathcal{E}}(\hat{a}{e}^{i\theta }-{\hat{a}}^{\dagger }{e}^{-i\theta }).\) Here as in the second example, we work in natural units. Furthermore, we set ω = 1 so that all other quantities appearing are in units of ω. In Fig. 2, we have chosen \(\theta =0,{\mathcal{E}}=2,\) and γ = 1/10. For the measurement, we chose the rotation matrix to be the identity, i.e., φ = 0, and we consider an ideal measurement Δ = 0, η = 1, with s = {0, 1, ∞}. Furthermore, the initial mean values of the oscillator quadratures is \(\bar{{\bf{x}}}(t=0)=(1,1)\). The drift and diffusion matrices are readily obtained as

$$A=\left(\begin{array}{*{20}{l}}-\gamma /2&\omega \\ -\omega &-\gamma /2\end{array}\right),$$
(16)
$$D={\gamma ({n}_{{\rm{th}}}+1/2){\mathbb{I}}}.$$
(17)

For the optical parametric oscillator, we chose the bath in the vacuum state nth = 0, which is a reasonable assumption for optical modes. The (effective) Hamiltonian of the system is given by

$${\hat{H}}_{s}=\frac{1}{2}{\hat{{\bf{x}}}}^{{\mathrm{T}}}\left(\begin{array}{*{20}{l}}0&-\chi \\ -\chi &0\end{array}\right)\hat{{\bf{x}}}.$$
(18)

The unconditional dynamics of the oscillator is stable only if γ > 2χ. The drift and diffusion matrices are given by

$$A=\left(\begin{array}{*{20}{l}}-\chi -\gamma /2&0\\ 0&\chi -\gamma /2\end{array}\right),$$
(19)
$$D={\gamma ({{n}_{{\rm{th}}}}+1/2){\Bbb{I}}}.$$
(20)

Note that, as expected, only the reversible part of the drift matrix (A) changes with respect to the previous example. In Fig. 2, we set χ = 1 so that all other quantities appearing are in units of χ. We chose the coupling constant to be γ = 2.001, i.e., the parametric oscillator is close to the instability point γ = 2χ. The initial expectation value of the quadratures is chosen in the origin of phase space. For the measurement, we chose the rotation matrix to be the identity, i.e., φ = 0, and we consider an efficient measurement (η = 1) with a small additive noise Δ = 0.1. As before s = {0, 1, ∞}. We add Gaussian noise in such a way to have an unconditional dynamics which, for different detection schemes, leads the system to steady states with different purities. It should be noted that for a thermal bath at zero temperature and ideal general-dyne measurements, the steady state of the conditional dynamics would always be a pure state (in contrast to the unconditional steady state which is always a mixed state).