Abstract
Hippocampal replay during sharp-wave ripple events (SWRs) is thought to drive memory consolidation in hippocampal and cortical circuits. Changes in neocortical activity can precede SWR events, but whether and how these changes influence the content of replay remains unknown. Here we show that during sleep there is a rapid cortical–hippocampal–cortical loop of information flow around the times of SWRs. We recorded neural activity in auditory cortex (AC) and hippocampus of rats as they learned a sound-guided task and during sleep. We found that patterned activation in AC precedes and predicts the subsequent content of hippocampal activity during SWRs, while hippocampal patterns during SWRs predict subsequent AC activity. Delivering sounds during sleep biased AC activity patterns, and sound-biased AC patterns predicted subsequent hippocampal activity. These findings suggest that activation of specific cortical representations during sleep influences the identity of the memories that are consolidated into long-term stores.
This is a preview of subscription content, access via your institution
Access options
Subscription info for Japanese customers
We have a dedicated website for our Japanese customers. Please go to natureasia.com to subscribe to this journal.
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Frankland, P.W. & Bontempi, B. The organization of recent and remote memories. Nat. Rev. Neurosci. 6, 119–130 (2005).
Squire, L.R. & Alvarez, P. Retrograde amnesia and memory consolidation: a neurobiological perspective. Curr. Opin. Neurobiol. 5, 169–177 (1995).
Eichenbaum, H. A cortical-hippocampal system for declarative memory. Nat. Rev. Neurosci. 1, 41–50 (2000).
Buzsáki, G. The hippocampo-neocortical dialogue. Cereb. Cortex 6, 81–92 (1996).
Buzsáki, G. Hippocampal sharp wave-ripple: a cognitive biomarker for episodic memory and planning. Hippocampus 25, 1073–1188 (2015).
Lisman, J. & Morris, R.G. Memory. Why is the cortex a slow learner? Nature 411, 248–249 (2001).
Peyrache, A., Khamassi, M., Benchenane, K., Wiener, S.I. & Battaglia, F.P. Replay of rule-learning related neural patterns in the prefrontal cortex during sleep. Nat. Neurosci. 12, 919–926 (2009).
Ego-Stengel, V. & Wilson, M.A. Disruption of ripple-associated hippocampal activity during rest impairs spatial learning in the rat. Hippocampus 20, 1–10 (2010).
Girardeau, G. & Zugaro, M. Hippocampal ripples and memory consolidation. Curr. Opin. Neurobiol. 21, 452–459 (2011).
Inostroza, M. & Born, J. Sleep for preserving and transforming episodic memory. Annu. Rev. Neurosci. 36, 79–102 (2013).
Sadowski, J.H., Jones, M.W. & Mellor, J.R. Sharp-wave ripples orchestrate the induction of synaptic plasticity during reactivation of place cell firing patterns in the hippocampus. Cell Rep. 14, 1916–1929 (2016).
Oliva, A., Fernández-Ruiz, A., Buzsáki, G. & Berényi, A. Role of hippocampal CA2 region in triggering sharp-wave ripples. Neuron 91, 1342–1355 (2016).
Suzuki, S.S. & Smith, G.K. Spontaneous EEG spikes in the normal hippocampus. IV. Effects of medial septum and entorhinal cortex lesions. Electroencephalogr. Clin. Neurophysiol. 70, 73–83 (1988).
Chrobak, J.J. & Buzsáki, G. High-frequency oscillations in the output networks of the hippocampal-entorhinal axis of the freely behaving rat. J. Neurosci. 16, 3056–3066 (1996).
Isomura, Y. et al. Integration and segregation of activity in entorhinal-hippocampal subregions by neocortical slow oscillations. Neuron 52, 871–882 (2006).
Jadhav, S.P., Rothschild, G., Roumis, D.K. & Frank, L.M. Coordinated excitation and inhibition of prefrontal ensembles during awake hippocampal sharp-wave ripple events. Neuron 90, 113–127 (2016).
Ji, D. & Wilson, M.A. Coordinated memory replay in the visual cortex and hippocampus during sleep. Nat. Neurosci. 10, 100–107 (2007).
Sirota, A., Csicsvari, J., Buhl, D. & Buzsáki, G. Communication between neocortex and hippocampus during sleep in rodents. Proc. Natl. Acad. Sci. USA 100, 2065–2069 (2003).
Wierzynski, C.M., Lubenov, E.V., Gu, M. & Siapas, A.G. State-dependent spike-timing relationships between hippocampal and prefrontal circuits during sleep. Neuron 61, 587–596 (2009).
Eschenko, O., Ramadan, W., Mölle, M., Born, J. & Sara, S.J. Sustained increase in hippocampal sharp-wave ripple activity during slow-wave sleep after learning. Learn. Mem. 15, 222–228 (2008).
Girardeau, G., Benchenane, K., Wiener, S.I., Buzsáki, G. & Zugaro, M.B. Selective suppression of hippocampal ripples impairs spatial memory. Nat. Neurosci. 12, 1222–1223 (2009).
Jadhav, S.P., Kemere, C., German, P.W. & Frank, L.M. Awake hippocampal sharp-wave ripples support spatial memory. Science 336, 1454–1458 (2012).
Diekelmann, S. & Born, J. The memory function of sleep. Nat. Rev. Neurosci. 11, 114–126 (2010).
Maingret, N., Girardeau, G., Todorova, R., Goutierre, M. & Zugaro, M. Hippocampo-cortical coupling mediates memory consolidation during sleep. Nat. Neurosci. 19, 959–964 (2016).
Bendor, D. & Wilson, M.A. Biasing the content of hippocampal replay during sleep. Nat. Neurosci. 15, 1439–1444 (2012).
Remondes, M. & Schuman, E.M. Role for a cortical input to hippocampal area CA1 in the consolidation of a long-term memory. Nature 431, 699–703 (2004).
Fritz, J., Shamma, S., Elhilali, M. & Klein, D. Rapid task-related plasticity of spectrotemporal receptive fields in primary auditory cortex. Nat. Neurosci. 6, 1216–1223 (2003).
Nelken, I. Stimulus-specific adaptation and deviance detection in the auditory system: experiments and models. Biol. Cybern. 108, 655–663 (2014).
Letzkus, J.J. et al. A disinhibitory microcircuit for associative fear learning in the auditory cortex. Nature 480, 331–335 (2011).
Rothschild, G., Cohen, L., Mizrahi, A. & Nelken, I. Elevated correlations in neuronal ensembles of mouse auditory cortex following parturition. J. Neurosci. 33, 12851–12861 (2013).
Weinberger, N.M. Specific long-term memory traces in primary auditory cortex. Nat. Rev. Neurosci. 5, 279–290 (2004).
Recanzone, G.H., Schreiner, C.E. & Merzenich, M.M. Plasticity in the frequency representation of primary auditory cortex following discrimination training in adult owl monkeys. J. Neurosci. 13, 87–103 (1993).
Sacco, T. & Sacchetti, B. Role of secondary sensory cortices in emotional memory storage and retrieval in rats. Science 329, 649–656 (2010).
Rothschild, G. & Mizrahi, A. Global order and local disorder in brain maps. Annu. Rev. Neurosci. 38, 247–268 (2015).
Wilson, M.A. & McNaughton, B.L. Reactivation of hippocampal ensemble memories during sleep. Science 265, 676–679 (1994).
Skaggs, W.E. & McNaughton, B.L. Replay of neuronal firing sequences in rat hippocampus during sleep following spatial experience. Science 271, 1870–1873 (1996).
Siapas, A.G. & Wilson, M.A. Coordinated interactions between hippocampal ripples and cortical spindles during slow-wave sleep. Neuron 21, 1123–1128 (1998).
Staresina, B.P. et al. Hierarchical nesting of slow oscillations, spindles and ripples in the human hippocampus during sleep. Nat. Neurosci. 18, 1679–1686 (2015).
Clemens, Z. et al. Temporal coupling of parahippocampal ripples, sleep spindles and slow oscillations in humans. Brain 130, 2868–2878 (2007).
Issa, E.B. & Wang, X. Sensory responses during sleep in primate primary and secondary auditory cortex. J. Neurosci. 28, 14467–14480 (2008).
Schreiner, T. & Rasch, B. Boosting vocabulary learning by verbal cueing during sleep. Cereb. Cortex 25, 4169–4179 (2015).
Rudoy, J.D., Voss, J.L., Westerberg, C.E. & Paller, K.A. Strengthening individual memories by reactivating them during sleep. Science 326, 1079 (2009).
Logothetis, N.K. et al. Hippocampal-cortical interaction during periods of subcortical silence. Nature 491, 547–553 (2012).
Lesburguères, E. et al. Early tagging of cortical networks is required for the formation of enduring associative memory. Science 331, 924–928 (2011).
Cowansage, K.K. et al. Direct reactivation of a coherent neocortical memory of context. Neuron 84, 432–441 (2014).
Luczak, A., Barthó, P. & Harris, K.D. Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron 62, 413–425 (2009).
Insausti, R., Herrero, M.T. & Witter, M.P. Entorhinal cortex of the rat: cytoarchitectonic subdivisions and the origin and distribution of cortical efferents. Hippocampus 7, 146–183 (1997).
Furtak, S.C., Wei, S.M., Agster, K.L. & Burwell, R.D. Functional neuroanatomy of the parahippocampal region in the rat: the perirhinal and postrhinal cortices. Hippocampus 17, 709–722 (2007).
Swanson, L.W. & Köhler, C. Anatomical evidence for direct projections from the entorhinal area to the entire cortical mantle in the rat. J. Neurosci. 6, 3010–3023 (1986).
Lansink, C.S., Goltstein, P.M., Lankelma, J.V., McNaughton, B.L. & Pennartz, C.M. Hippocampus leads ventral striatum in replay of place-reward information. PLoS Biol. 7, e1000173 (2009).
Karlsson, M.P. & Frank, L.M. Network dynamics underlying the formation of sparse, informative representations in the hippocampus. J. Neurosci. 28, 14271–14281 (2008).
Karlsson, M.P. & Frank, L.M. Awake replay of remote experiences in the hippocampus. Nat. Neurosci. 12, 913–918 (2009).
Cheng, S. & Frank, L.M. New experiences enhance coordinated neural activity in the hippocampus. Neuron 57, 303–313 (2008).
Peyrache, A., Benchenane, K., Khamassi, M., Wiener, S.I. & Battaglia, F.P. Principal component analysis of ensemble recordings reveals cell assemblies at high temporal resolution. J. Comput. Neurosci. 29, 309–325 (2010).
Acknowledgements
We thank L. Tian, K. Kay, J. Yu, E. Anderson, M. Sosa, A. Eban-Rothschild, M. Karlsson and C. Schreiner for discussion and suggestions, and L. Tian, I. Grossrubatscher and S. Harris for technical assistance. This work was supported by the Howard Hughes Medical Institute, an NIH grant (R01 MH090188) to L.M.F. and an EMBO long-term postdoctoral fellowship and an ELSC postdoctoral fellowship to G.R.
Author information
Authors and Affiliations
Contributions
G.R. and L.M.F. conceived the study. G.R. conducted the experiments. G.R. analyzed the data. E.E. contributed to the generalized linear model analysis. G.R. and L.M.F. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Integrated supplementary information
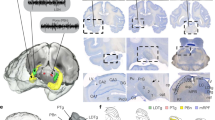
Supplementary Figure 1 Histology
Nissl stained histological coronal sections showing example electrode tracks and lesion locations. Top: auditory cortex, Bottom: dorsal CA1. Scale bars are 1 mm.
Supplementary Figure 2 Rest, sleep and SWR counts
Rest, sleep and SWR data per silent sleep epoch (left) and per day across silent sleep epochs (right). From top to bottom: Silent rest epoch durations, NREM sleep during silent rest epochs, NREM sleep proportion out of rest time, all SWR counts, temporally well-isolated SWR counts (after removal of SWRs at temporal offsets of <500ms from other SWRs, as being used for SWR modulation and GLM predictions), SWR rates of temporally well-isolated SWR counts.
Supplementary Figure 3 Same temporal pattern of SWR modulation using alternative SWR-modulation criterion
Parallel figures to Fig. 2a-c but when applying an SWR-modulation criterion of P<0.05 across entire daily datasets. The same temporal patterns are apparent.
(a) SWR-triggered mean spiking histograms of all SWR-modulated AC neurons. Each row shows the z-scored mean SWR-triggered spiking histogram of one neuron. Neurons are ordered by timing of peak firing in -250 ms to 250 ms window relative to SWR onset
(b) Same as (a) for CA1 neurons.
(c) Mean z-scored SWR-triggered spiking histogram across all SWR-modulated neurons for AC (green) and CA1 (orange). Shaded area indicates sem. Traces correspond to the mean±sem of data in (a) and (b).
Supplementary Figure 4 Reactivation of awake patterns during sleep in auditory cortex
(a) Histogram of reactivation amplitudes for the example in Fig. 1g.
(b) Distribution of reactivation skewness values across all epochs
(c) SWR-triggered reactivation as in Fig. 1h, but using full correlation matrix from awake state as template instead of first principle component. This alternative analysis demonstrates that the reactivation shown in Figure 1 is not dependent on the choice of the first principle component as the reactivation measure.
Supplementary Figure 5 SWR-triggered LFP in auditory cortex
(a) Mean z-scored SWR-triggered spectrogram of AC local field potential. We extracted the LFP around all SWRs across the dataset and calculated the spectrogram around each SWR. Spectrograms were averaged across tetrodes in the same recordings, and z-scored by the average power across frequencies. The spectrogram shows an increase in power in the delta and spindle bands during SWRs.
(b) Mean SWR-triggered raw local field potential
(c) SWR-triggered power in the delta band. We filtered the LFP in the delta band (1-4 Hz) and identified its envelope using the Hilbert transform. We extracted the delta envelope around all SWRs in the dataset and z-scored each of them. The shaded area is mean±SEM. As seen in ‘a’, the delta power increases during SWRs, with an increase before SWR onset.
(d) SWR-triggered power in the spindle band. Similar to ‘c’ but in the spindle band (8-20 Hz). As seen in ‘a’, power in the spindle band shows an increase during SWRs.
Supplementary Figure 6 Predicting SWR occurrence from AC ensemble spiking patterns
To predict SWR occurrences we used a cross-validated GLM approach. For each silent sleep epoch we binned all AC spike counts into 200 ms bins and created a vector of 0/1’s of the same length indicating bins in which SWRs occurred. We used 5-fold cross validation: the data was divided into 5 equally sized datasets, balanced in the number of SWRs. For each fold, 4 folds were used to train a binomial GLM model to predict SWR occurrence from the AC firing patterns, and the remaining fold was used as a test set. To quantify performance of each fold, the GLM model was applied to predict the likelihood of SWR occurrences in all bins from the AC ensemble spiking in the test fold. The test error was defined as the mean absolute difference between the prediction and real rates. Test errors were averaged across folds. As control, we calculated the error across 100 shuffles of the test sets. Prediction gain for each dataset was defined as the error of the shuffled data divided by the error of the original data.
(a) Prediction gain of SWR occurrence. Each column at time t depicts the prediction gain of SWR occurrence at time 0 from predictor AC patterns at time t. Prediction was measured as described above. Gray is shuffled data, in which the AC patterns were shuffled relative to SWR times. Error bars are SEM.
(b) Significance of median larger than 1, corresponding to the data in ‘a’. P-values were measured using a one-sided Wilcoxon signed-rank test and presented as –log10(P)
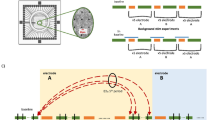
Supplementary Figure 7 Visual illustration of GLM cross-validation method
The overall procedure was as follows: For each combination of predictor ensemble and predicted cell in a given time window, the predictor data consisted of the ensemble patterns (binned spiked counts) across SWRs, and the predicted data consisted of the single-cell SWR responses (binned spiked counts) across SWRs. We then performed 5-fold cross validation by randomly partitioning the daily SWRs into 5 equal-sized sets. For each of the 5 folds, we used 4 of 5 folds to train the GLM model, and the remaining fold to test. For the test phase, the model derived from the training phase was applied to the predictor ensemble data in the test set, yielding predictions for the predicted cell firing across SWRs. The prediction error was the mean absolute difference between the predicted spike counts and the real spike counts. A baseline prediction error was calculated as the mean prediction errors across 100 random shuffles of the predicted firing rates across SWRs. The real and shuffled prediction errors were then averaged across the 5 folds. Prediction gain for one predictor ensemble/predicted cell combination in one time window was defined as the shuffled prediction error divided by the real prediction error. For comparison, we repeated the exact same procedure described above on 100 random shuffles of the entire original dataset, where shuffling entailed random matching of activity patterns in the predictor and predicted data.
Supplementary Figure 8 Alternative statistical tests for GLM prediction significance
(a) Prediction of CA1 single-cell spiking during SWRs from ensemble spiking patterns in AC across varying time windows (n = 107 predicted CA1 cells). Black error bars indicate mean ± s.e.m. prediction gain for real data. Grey dashed line indicates 1 (no gain). Columns represent varying time windows used as predictor data; predicted data is always the SWR time window (0 – 200 ms). This panel parallels Fig. 2g, but significance of prediction gain is tested against 1 using a two-tailed Wilcoxon signed rank test. CA1 spiking during SWRs could be significantly predicted better than shuffled data from AC ensemble spiking patterns in the -400 to -200 ms window (P=0.0061), -200 to 0 ms window (P=9.35e-5) and 0 to 200 ms window (P=1.22e-8), but not from the -600 to -400 ms window (P=0.7) (two-tailed Wilcoxon signed rank test of difference from 1).
(b) Same as (a), but in the opposite direction: prediction of AC single-cell spiking during SWRs from ensemble spiking in CA1 (n=152 predicted AC cells) using statistical test of difference from 1. AC spiking during SWRs could not be significantly predicted from pre-SWR CA1 ensemble spiking patterns, but could be predicted from CA1 spiking during the SWR (-600 to -400: P=0.845; -400 to -200: P=0.371; -200 to 0: P=0.769; 0 to 200: P=1.05e-6, two-tailed Wilcoxon signed rank test of difference from 1)
(c) Same as (a), but using an additional test of whether log(prediction gain) is different from 0. Results show the same pattern: -600 to -400: P=0.705; -400 to -200: P=0.0063; -200 to 0: P=9.6e-5; 0 to 200: P=1.29e-8, two-tailed Wilcoxon signed rank test of difference from 0.
(d) Same as (b), but using an additional test of whether log(prediction gain) is different from 0. Results show the same pattern: -600 to -400: P=0.851; -400 to -200: P=0.377; -200 to 0: P=0.76; 0 to 200: P=1.1e-6, two-tailed Wilcoxon signed rank test of difference from 0.
Supplementary Figure 9 Firing rate differences do not account for prediction patterns
(a) Firing rates of AC (top) and CA1 (bottom) cells across time bins relative to SWR times. Data are pooled across cells, SWRs and experiments. Firing rates in both AC and CA1 show a significant difference across time bins (P<10-10, one-way ANOVA).
(b) Same as in (a) but after firing rate equalization. For firing rates of a given predictor ensemble in a given time window, equalization was done by multiplying the firing rates of all neurons in the ensemble across all SWRs by a factor of 2.5/(observed mean) to yield a resulting mean of 2.5 across cells and SWRs. The resulting equalized firing rates did not show a significant difference across time bins (p>0.99, one-way ANOVA).
(c) Prediction gains paralleling Fig. 2g-h and Suppl. Fig. 8, when applied on firing-rate equalized data (b). The same prediction patterns across time bins and brain regions were observed as with original data. In the AC to CA1 direction (top): -600 to -400: P=0.697; -400 to -200: P=0.0061; -200 to 0: P=9.35e-5; 0 to 200: P=1.22e-8, two-tailed Wilcoxon signed rank test of difference from 1. In the CA1 to AC direction (bottom): -600 to -400: P=0.845; -400 to -200: P=0.371; -200 to 0: P=0.769; 0 to 200: P=1.05e-6, two-tailed Wilcoxon signed rank test of difference from 1.
(d) Upper bound of prediction gains of firing patterns in pre-SWR CA1 windows predicting AC SWR spiking. Upper bound was estimated by artificially sorting the original firing rates of each predictor cell across SWRs to match the firing rate order of the predicted cell. The upper bound of ~50% prediction gain indicates that lack of prediction in this direction in the original data is not due to lack of sufficient spikes. P<10-10 in all three windows, two-tailed Wilcoxon signed rank test of difference from 1
Supplementary Figure 10 Rate of significantly predictive ensemble–cell combinations
a. Fraction of individually significant (P<0.05) ensemble-cell predictions in the AC->CA1 direction. Significance was tested by comparing the prediction gain of each cross-validated model to the prediction gains obtained from 1000 shuffles. The P-value was defined as the rate of shuffles with gain higher than the data.
b. The same as in ‘a’ for the CA1->AC direction.
Supplementary Figure 11 Sound spectrograms
Spectrograms of the 4 auditory stimuli used.
Supplementary Figure 12 Additional examples of AC sound responses during sleep
Responses of 14 example AC cells to the auditory stimuli presented during sound sleep sessions. Each group of 8 panels shows the responses of one AC cell to the 4 different stimuli in one sleep sound epoch as in Fig. 3b. These data illustrate the strength, temporal profiles and diversity of the observed responses.
Supplementary Figure 13 Sound decoding from CA1 ensemble patterns during SWRs
Decoding was performed as in Figure 3e, but for CA1 ensemble firing patterns during the SWR. Decoding gain was not significantly different from 0 (P=0.172, cross-validated linear discriminant analysis, population test for mean larger than 0 using one-tailed t-test)
Supplementary Figure 14 Stimulus-specific SWR density across learning
(a)Stimulus-specific SWR density across learning, as in Fig. 5b, using alternative cutoffs for First/Later days, showing similar results. Left: First days are 1-2, Later days are >=3. Right: First days are 1-4, Later days are >=5.
(b)SWR density across days, for daily (first and last epochs combined, left), first daily epochs (middle) and last daily epochs (right). SWR density of non-target stimuli did not show a decreasing trend across days.
(c)Stimulus-specific SWR density across learning, as in Fig. 5b, but including SWR density in no-sound times (gray filled bars). Note that at later stages of learning, SWR density during target sound presentation did not differ from during no-sound.
(d)Stimulus-specific SWR density in First versus Later days. The first and last daily epochs were combined.
Supplementary information
Supplementary Text and Figures
Supplementary Figures 1–14 (PDF 2523 kb)
Rights and permissions
About this article
Cite this article
Rothschild, G., Eban, E. & Frank, L. A cortical–hippocampal–cortical loop of information processing during memory consolidation. Nat Neurosci 20, 251–259 (2017). https://doi.org/10.1038/nn.4457
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nn.4457
This article is cited by
-
Sleep microstructure organizes memory replay
Nature (2025)
-
Differential contribution of canonical and noncanonical NLGN3 pathways to early social development and memory performance
Molecular Brain (2024)
-
Emerging many-to-one weighted mapping in hippocampus-amygdala network underlies memory formation
Nature Communications (2024)
-
Spindle-locked ripples mediate memory reactivation during human NREM sleep
Nature Communications (2024)
-
Cortical reactivations predict future sensory responses
Nature (2024)