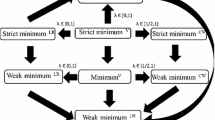
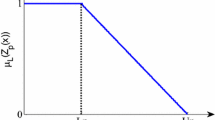
Abstract
Many practical optimization problems are characterized by some flexibility in the problem constraints, where this flexibility can be exploited for additional trade-off between improving the objective function and satisfying the constraints. Fuzzy sets have proven to be a suitable representation for modeling this type of soft constraints. Conventionally, the fuzzy optimization problem in such a setting is defined as the simultaneous satisfaction of the constraints and the goals. No additional distinction is assumed to exist amongst the constraints and the goals. This paper proposes an extension of this model for satisfying the problem constraints and the goals, where preference for different constraints and goals can be specified by the decision-maker. The difference in the preference for the constraints is represented by a set of associated weight factors, which influence the nature of trade-off between improving the optimization objectives and satisfying various constraints. Simultaneous weighted satisfaction of various criteria is modeled by using the recently proposed weighted extensions of (Archimedean) fuzzy t-norms. The weighted satisfaction of the problem constraints and goals are demonstrated by using a simple fuzzy linear programming problem. The framework, however, is more general, and it can also be applied to fuzzy mathematical programming problems and multi-objective fuzzy optimization.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Bellman, R. E., & Zadeh, L. A. (1970). Decision-making in a fuzzy environment. Management Science, 17(4): 141–164.
Dubois, D., Fargier, H., & Prade, H. (1994). Propagation and satisfaction of flexible constraints. In Yager, R. R., & Zadeh, L. A. eds., Fuzzy Sets, Neural Networks and Soft Computing, pages 166–187. Van Nostrand Reinhold, New York.
Dubois, D., Grenier, P., Prade, H., & Sabbadin, R. (1998). A fuzzy constraint satisfaction problem in the wine industry. Journal of Intelligent and Fuzzy Systems, 6: 361–374.
Dyckhoff, H., & Pedrycz, W. (1984). Generalized means as model of compensative connectives. Fuzzy Sets and Systems, 14: 143–154.
Gill, P. E., Murray, W., & Wright, M. (1981). Practical Optimization. Academic Press, New York.
Goldberg, D. E. (1989). Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley, New York.
Grabisch, M., Nguyen, H. T., & Walker, E. A. (1995). Fundamentals of Uncertainty Calculi with Applications to Fuzzy Inference, Vol. 30 of B: Mathematical and Statistical Methods. Kluwer Academic Publishers, Dordrecht.
Kaymak, U. (1998). Fuzzy decision making with control applications. Ph.D. thesis, Delft University of Technology, Delft, the Netherlands.
Kaymak, U., & Sousa, J. M. (1997). Model based fuzzy predictive control applied to a simulated gantry crane. In Proceedings of 2nd Asian Control Conference, Seoul, Korea, pages III-455–III-458.
Kaymak, U., & van Nauta Lemke, H. R. (1993). A parametric generalized goal function for fuzzy decision making with unequally weighted objectives. In Proceedings of the Second IEEE International Conference on Fuzzy Systems, Vol. 2, pages 1156–1160.
Kaymak, U., & van Nauta Lemke, H. R. (1998). A sensitivity analysis approach to introducing weight factors into decision functions in fuzzy multicriteria decision making. Fuzzy Sets and Systems, 97(2): 169–182.
Kaymak, U., van Nauta Lemke, H. R., & den Boer, T. (1998). A sensitivity-based analysis of weighted fuzzy aggregation. In Proceedings of the IEEE World Congress on Computational Intelligence. Anchorage, Alaska, pages 755–760.
Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. (1983). Optimization by simulated annealing. Science, 220(4598): 671–680.
Klir, G. J., & Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall, Upper Saddle River, NJ.
Nelder, J. A., & Mead, R. (1965). A simplex method for function minimization. Computer Journal, 7: 308–313.
Sousa, J. M. (2000). Optimization issues in predictive control with fuzzy objective functions. International Journal of Intelligent Systems, 15(9): 879–899.
van Nauta Lemke, H. R., Dijkman, J. G., van Haeringen, H., & Pleeging, M. (1983). A characteristic optimism factor in fuzzy decision-making. In Proc. IFAC Symp. on Fuzzy Information, Knowledge Representation and Decision Analysis, Marseille, France, pages 283–288.
Yager, R. R. (1978). Fuzzy decision making including unequal objectives. Fuzzy Sets and Systems, 1: 87–95.
Yager, R. R. (1984). General multiple-objective decision functions and linguistically quantified statements. International Journal of Man-Machine Studies, 21: 389–400.
Yager, R. R. (1988). On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Transactions on Systems, Man and Cybernetics, 18(1): 183–190.
Yager, R. R., & Filev, D. P. (1994). Essentials of Fuzzy Modelling and Control. John Wiley, New York.
Zimmermann, H. J. (1976). Description and optimization of fuzzy systems. International Journal of General Systems, 2: 209–215.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Kaymak, U., Sousa, J.M. Weighted Constraint Aggregation in Fuzzy Optimization. Constraints 8, 61–78 (2003). https://doi.org/10.1023/A:1021998611875
Issue Date:
DOI: https://doi.org/10.1023/A:1021998611875