Published online by Cambridge University Press: 22 June 2020
In 2004 Atserias, Kolaitis, and Vardi proposed 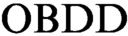 $\text {OBDD}$
-based propositional proof systems that prove unsatisfiability of a CNF formula by deduction of an identically false
$\text {OBDD}$
-based propositional proof systems that prove unsatisfiability of a CNF formula by deduction of an identically false 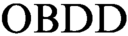 $\text {OBDD}$
from
$\text {OBDD}$
from 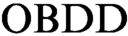 $\text {OBDD}$
s representing clauses of the initial formula. All
$\text {OBDD}$
s representing clauses of the initial formula. All 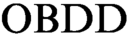 $\text {OBDD}$
s in such proofs have the same order of variables. We initiate the study of
$\text {OBDD}$
s in such proofs have the same order of variables. We initiate the study of 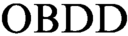 $\text {OBDD}$
based proof systems that additionally contain a rule that allows changing the order in
$\text {OBDD}$
based proof systems that additionally contain a rule that allows changing the order in 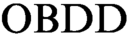 $\text {OBDD}$
s. At first we consider a proof system
$\text {OBDD}$
s. At first we consider a proof system 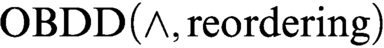 $\text {OBDD}(\land , \text{reordering})$
that uses the conjunction (join) rule and the rule that allows changing the order. We exponentially separate this proof system from
$\text {OBDD}(\land , \text{reordering})$
that uses the conjunction (join) rule and the rule that allows changing the order. We exponentially separate this proof system from 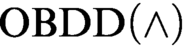 $\text {OBDD}(\land )$
proof system that uses only the conjunction rule. We prove exponential lower bounds on the size of
$\text {OBDD}(\land )$
proof system that uses only the conjunction rule. We prove exponential lower bounds on the size of 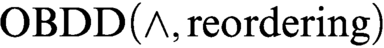 $\text {OBDD}(\land , \text{reordering})$
refutations of Tseitin formulas and the pigeonhole principle. The first lower bound was previously unknown even for
$\text {OBDD}(\land , \text{reordering})$
refutations of Tseitin formulas and the pigeonhole principle. The first lower bound was previously unknown even for 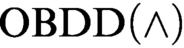 $\text {OBDD}(\land )$
proofs and the second one extends the result of Tveretina et al. from
$\text {OBDD}(\land )$
proofs and the second one extends the result of Tveretina et al. from 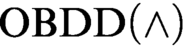 $\text {OBDD}(\land )$
to
$\text {OBDD}(\land )$
to 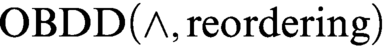 $\text {OBDD}(\land , \text{reordering})$
.
$\text {OBDD}(\land , \text{reordering})$
.
In 2001 Aguirre and Vardi proposed an approach to the propositional satisfiability problem based on 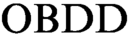 $\text {OBDD}$
s and symbolic quantifier elimination (we denote algorithms based on this approach as
$\text {OBDD}$
s and symbolic quantifier elimination (we denote algorithms based on this approach as 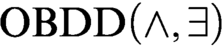 $\text {OBDD}(\land , \exists )$
algorithms). We augment these algorithms with the operation of reordering of variables and call the new scheme
$\text {OBDD}(\land , \exists )$
algorithms). We augment these algorithms with the operation of reordering of variables and call the new scheme 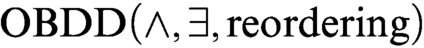 $\text {OBDD}(\land , \exists , \text{reordering})$
algorithms. We notice that there exists an
$\text {OBDD}(\land , \exists , \text{reordering})$
algorithms. We notice that there exists an 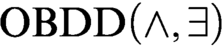 $\text {OBDD}(\land , \exists )$
algorithm that solves satisfiable and unsatisfiable Tseitin formulas in polynomial time (a standard example of a hard system of linear equations over
$\text {OBDD}(\land , \exists )$
algorithm that solves satisfiable and unsatisfiable Tseitin formulas in polynomial time (a standard example of a hard system of linear equations over 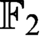 $\mathbb {F}_2$
), but we show that there are formulas representing systems of linear equations over
$\mathbb {F}_2$
), but we show that there are formulas representing systems of linear equations over 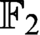 $\mathbb {F}_2$
that are hard for
$\mathbb {F}_2$
that are hard for 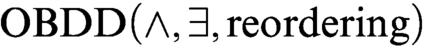 $\text {OBDD}(\land , \exists , \text{reordering})$
algorithms. Our hard instances are satisfiable formulas representing systems of linear equations over
$\text {OBDD}(\land , \exists , \text{reordering})$
algorithms. Our hard instances are satisfiable formulas representing systems of linear equations over 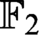 $\mathbb {F}_2$
that correspond to checksum matrices of error correcting codes.
$\mathbb {F}_2$
that correspond to checksum matrices of error correcting codes.
The present paper is an expansion of an earlier conference paper [17]. It includes the contents of [17] augmented with all the proofs that were omitted in the conference version. In addition, the paper contains a new deterministic construction of a hard example for  $\text {OBDD}(\land , \exists )$
algorithms.
$\text {OBDD}(\land , \exists )$
algorithms.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.