Published online by Cambridge University Press: 07 May 2019
Unsteady flow generated by a point-like source takes place into a  $d$-dimensional porous formation where the spatial variability of the hydraulic conductivity
$d$-dimensional porous formation where the spatial variability of the hydraulic conductivity 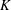 $K$ is modelled within a stochastic framework that regards
$K$ is modelled within a stochastic framework that regards 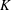 $K$ as a stationary, normally distributed random space function (rsf). As a consequence, the hydraulic head
$K$ as a stationary, normally distributed random space function (rsf). As a consequence, the hydraulic head 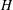 $H$ becomes also stochastic, and we aim at quantifying its uncertainty. Towards this aim, we have derived the head covariance by means of a perturbation expansion which regards the variance
$H$ becomes also stochastic, and we aim at quantifying its uncertainty. Towards this aim, we have derived the head covariance by means of a perturbation expansion which regards the variance 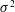 $\unicode[STIX]{x1D70E}^{2}$ of the zero mean rsf
$\unicode[STIX]{x1D70E}^{2}$ of the zero mean rsf $\unicode[STIX]{x1D700}=1-K/\langle K\rangle$ (hereafter
$\unicode[STIX]{x1D700}=1-K/\langle K\rangle$ (hereafter 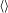 $\langle \rangle$ being the ensemble average operator) as a small parameter. The analytical results are expressed in terms of multiple quadratures which are markedly reduced after adopting specific autocorrelation
$\langle \rangle$ being the ensemble average operator) as a small parameter. The analytical results are expressed in terms of multiple quadratures which are markedly reduced after adopting specific autocorrelation 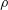 $\unicode[STIX]{x1D70C}$ for
$\unicode[STIX]{x1D70C}$ for  $\unicode[STIX]{x1D700}$. This enables one to obtain simple results providing straightforward physical insight into the spatial distribution of
$\unicode[STIX]{x1D700}$. This enables one to obtain simple results providing straightforward physical insight into the spatial distribution of 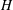 $H$ as a consequence of the heterogeneity of
$H$ as a consequence of the heterogeneity of 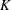 $K$. In view of those applications (pumping tests) aiming at the identification of the hydraulic properties of geological formations, we have focused on a flow generated by a source of instantaneous and constant strength. The attainment of the large time (steady-state) regime is studied in detail.
$K$. In view of those applications (pumping tests) aiming at the identification of the hydraulic properties of geological formations, we have focused on a flow generated by a source of instantaneous and constant strength. The attainment of the large time (steady-state) regime is studied in detail.
Present address: Division of Water Resources Management and Biosystems Engineering, via Universitá 100, I80055 Portici (NA), Italy. Email address for correspondence: gerardo.severino@unina.it
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.