Implementation and Evaluation of Breaking Detection Criteria for a Hybrid Boussinesq Model | Water Waves
Skip to main content
Springer Nature Link
Log in

Implementation and Evaluation of Breaking Detection Criteria for a Hybrid Boussinesq Model

  • Original Article
  • Published:
Water Waves Aims and scope Submit manuscript

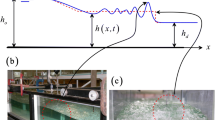
Abstract

The aim of the present work has been to develop a model able to represent the propagation and transformation of waves in nearshore areas. The focus is on the phenomena of wave breaking, shoaling, and run-up. These different phenomena are represented through a hybrid approach obtained by the coupling of non-linear Shallow Water equations with the extended Boussinesq equations of Madsen and Sørensen. The novelty is the switch tool between the two modelling equations: a critical free surface Froude criterion. This is based on a physically meaningful new approach to detect wave breaking, which corresponds to the steepening of the wave’s crest which turns into a roller. To allow for an appropriate discretization of both types of equations, we consider a finite element Upwind Petrov Galerkin method with a novel limiting strategy that guarantees the preservation of smooth waves as well as the monotonicity of the results in presence of discontinuities. We provide a detailed discussion of the implementation of the newly proposed detection method, as well as of two other well-known criteria which are used for comparison. An extensive benchmarking on several problems involving different wave phenomena and breaking conditions allows to show the robustness of the numerical method proposed, as well as to assess the advantages and limitations of the different detection methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

Notes

  1. Matrix absolute values are computed, as usual, by means of an eigen-decomposition.

References

  1. Abgrall, R., Ricchiuto, M.: High-order methods for CFD. In: Erwin Stein, RdB, Hughes, T.J. (eds.) Encyclopedia of Computational Mechanics Second Edition, pp. 1–54. Wiley Online Library, Oxford (2017)

    Google Scholar 

  2. Bacigaluppi, P., Ricchiuto, M., Bonneton, P.: Upwind Stabilized Finite Element Modelling of Non-hydrostatic Wave Breaking and Run-up. Research Report RR-8536, INRIA (2014)

  3. Bacigaluppi, P., Ricchiuto, M., Bonneton, P.: A 1D stabilized finite element model for non-hydrostatic wave breaking and run-up. In: Fuhrmann, J., Ohlberger, M., Rohde, C. (eds.) Finite Volumes for Complex Applications VII-Elliptic, Parabolic and Hyperbolic Problems, pp. 779–790. Springer, Cham (2014)

    MATH  Google Scholar 

  4. Beji, S., Battjes, J.: Experimental investigation of wave propagation over a bar. Coast. Eng. 19(1–2), 151–162 (1993)

    Google Scholar 

  5. Bjørkavåg, M., Kalisch, H.: Wave breaking in Boussinesq models for undular bores. Phys. Lett. A 375(14), 1570–1578 (2011)

    MATH  Google Scholar 

  6. Bonneton, P.: Modelling of periodic wave transformation in the inner surf zone. Ocean Eng. 34(10), 1459–1471 (2007)

    Google Scholar 

  7. Borthwick, A.G.L., Ford, M., Weston, B.P., Taylor, P.H., Stansby, P.K.: Solitary wave transformation, breaking and run-up at a beach. Proc. Inst. Civ. Eng. Maritime Eng. 159(3), 97–105 (2006)

    Google Scholar 

  8. Briganti, R., Musumeci, R.E., Bellotti, G., Brocchini, M., Foti, E.: Boussinesq modeling of breaking waves: description of turbulence. J. Geophys. Res. Oceans 109(C07015) (2004)

  9. Brun, M.K., Kalisch, H.: Convective wave breaking in the KdV equation. Anal. Math. Phys. 8(1), 57–75 (2018)

    MathSciNet  MATH  Google Scholar 

  10. Buhr Hansen, J., Svendsen, I.: Regular waves in shoaling water, experimental data. Tech. Rep. 21, Institute of Hydrodynamics and Hydraulic Engineering, Technical University of Denmark (1979)

  11. Castro, M., Ferreiro, A., García-Rodríguez, J., González-Vida, J., Macías, J., Parés, C., Vázquez-Cendón, M.: The numerical treatment of wet/dry fronts in shallow flows: application to one-layer and two-layer systems. Math. Comput. Model. 42(3–4), 419–439 (2005)

    MathSciNet  MATH  Google Scholar 

  12. Cea, L., Vázquez-Cendón, M.: Unstructured finite volume discretisation of bed friction and convective flux in solute transport models linked to the shallow water equations. J. Comput. Phys. 231(8), 3317–3339 (2012)

    MathSciNet  MATH  Google Scholar 

  13. Chanson, H.: Hydraulics of Open Channel Flow. Elsevier, Oxford (2004)

    Google Scholar 

  14. Cienfuegos, R., Barthélemy, E., Bonneton, P.: Wave-breaking model for Boussinesq-type equations including roller effects in the mass conservation equation. J. Waterw. Port Coast. Ocean Eng. 136(1), 10–26 (2009)

    Google Scholar 

  15. Delis, A., Kazolea, M., Kampanis, N.: A robust high-resolution finite volume scheme for the simulation of long waves over complex domains. Int. J. Num. Methods Fluids 56(4), 419–452 (2008)

    MathSciNet  MATH  Google Scholar 

  16. Dingemans, M.: Water Wave Propagation Over Uneven Bottoms: Linear wave propagation. Advanced series on ocean engineering. World Scientific Publishing Co Pte Ltd, Singapore (1997)

    MATH  Google Scholar 

  17. Favre, H.: Étude théorique et expérimentale des ondes de translation dans les canaux découverts. Publications du Laboratoire de recherches hydrauliques annexé á l’École polytechnique fédérale de Zurich. Dunod (1935)

  18. Filippini, A., Bellec, S., Colin, M., Ricchiuto, M.: On the nonlinear behavior of Boussinesq type models: amplitude-velocity vs amplitude-flux forms. Coast. Eng. 99, 109–123 (2015)

    Google Scholar 

  19. Filippini, A., Kazolea, M., Ricchiuto, M.: A flexible genuinely nonlinear approach for wave propagation, breaking and run-up. J. Comput. Phys. 310, 381–417 (2016)

    MathSciNet  MATH  Google Scholar 

  20. Harten, A., Hyman, J.: Self adjusting grid methods for one-dimensional hyperbolic conservation laws. J. Comput. Phys. 50(2), 235–269 (1983)

    MathSciNet  MATH  Google Scholar 

  21. Kazolea, M.: Personal communication.

  22. Kazolea, M., Delis, A.: A well-balanced shock-capturing hybrid finite volume-finite difference numerical scheme for extended 1D Boussinesq models. Appl. Num. Math. 67, 167–186 (2013)

    MathSciNet  MATH  Google Scholar 

  23. Kazolea, M., Ricchiuto, M.: On wave breaking for Boussinesq-type models. Ocean Model. 123, 16–39 (2018)

    Google Scholar 

  24. Kazolea, M., Delis, A.I., Synolakis, C.E.: Numerical treatment of wave breaking on unstructured finite volume approximations for extended Boussinesq-type equations. J. Comput. Phys. 271, 281–305 (2014)

    MathSciNet  MATH  Google Scholar 

  25. Kennedy, A., Chen, Q., Kirby, J., Dalrymple, R.: Boussinesq modeling of wave transformation, breaking and run-up I: 1D. J. Waterw. Port Coast. Ocean Eng. 126(1), 39–47 (2000)

    Google Scholar 

  26. Kermani, M., Plett, E.: Modified entropy correction formula for the Roe scheme. In: 39th Aerospace Sciences Meeting and Exhibit, p. 83 (2001)

  27. Lannes, D.: The Water Waves Problem: Mathematical Analysis and Asymptotics. Mathematical Surveys and monographs. American Mathematical Society, Providence (2013)

    MATH  Google Scholar 

  28. LeVeque, R.J.: Finite Volume Methods for Hyperbolic Problems. Cambridge Texts in Applied Mathematics. Cambridge University Press, Cambridge (2002)

    Google Scholar 

  29. Longuet-Higgins, M.S.: On wave breaking and the equilibrium spectrum of wind-generated waves. Proc. R. Soc. Lond. A. Math. Phys. Sci. 310(1501), 151–159 (1969)

    Google Scholar 

  30. Madsen, P.A., Sørensen, O.R.: A new form of the Boussinesq equations with improved linear dispersion characteristics. Part 2. A slowly-varying bathymetry. Coast. Eng. 18(3–4), 183–204 (1992)

    Google Scholar 

  31. Madsen, P.A., Murray, R., Sørensen, O.R.: A new form of the Boussinesq equations with improved linear dispersion characteristics. Coast. Eng. 15(4), 371–388 (1991)

    Google Scholar 

  32. Melville, W., Rapp, R.J.: The surface velocity field in steep and breaking waves. J. Fluid Mech. 189, 1–22 (1988)

    Google Scholar 

  33. Okamoto, T., Basco, D.R.: The relative trough froude number for initiation of wave breaking: theory, experiments and numerical model confirmation. Coast. Eng. 53(8), 675–690 (2006)

    Google Scholar 

  34. Pelanti, M., Quartapelle, L., Vigevano, L.: A review of entropy fixes as applied to Roe’s linearization. Teaching material of the Aerospace and Aeronautics Department of Politecnico di Milano (2001)

  35. Ricchiuto, M., Bollermann, A.: Stabilized residual distribution for shallow water simulations. J. Comput. Phys. 228(4), 1071–1115 (2009)

    MathSciNet  MATH  Google Scholar 

  36. Ricchiuto, M., Filippini, A.: Upwind residual discretization of enhanced Boussinesq equations for wave propagation over complex bathymetries. J. Comput. Phys. 271, 306–341 (2014)

    MathSciNet  MATH  Google Scholar 

  37. Roeber, V., Cheung, K.F.: Boussinesq-type model for energetic breaking waves in fringing reef environments. Coast. Eng. 70, 1–20 (2012)

    Google Scholar 

  38. Schäffer, H.A., Madsen, P.A., Deigaard, R.: A boussinesq model for waves breaking in shallow water. Coast. Eng. 20(3–4), 185–202 (1993)

    Google Scholar 

  39. Shi, F., Kirby, J.T., Harris, J.C., Geiman, J.D., Grilli, S.T.: A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation. Ocean Model. 43, 36–51 (2012)

    Google Scholar 

  40. Shiach, J.B., Mingham, C.G.: A temporally second-order accurate Godunov-type scheme for solving the extended Boussinesq equations. Coast. Eng. 56(1), 32–45 (2009)

    Google Scholar 

  41. Skotner, C., Apelt, C.: Application of a Boussinesq model for the computation of breaking waves: Part 1: development and verification. Ocean Eng. 26(10), 905–925 (1999)

    Google Scholar 

  42. Sørensen, O.R., Schäffer, H.A., Sørensen, L.S.: Boussinesq-type modelling using an unstructured finite element technique. Coast. Eng. 50(4), 181–198 (2004)

    Google Scholar 

  43. Synolakis, C.E.: The runup of solitary waves. J. Fluid Mech. 185, 523–545 (1987)

    MathSciNet  MATH  Google Scholar 

  44. Tissier, M., Bonneton, P., Marche, F., Chazel, F., Lannes, D.: A new approach to handle wave breaking in fully non-linear Boussinesq models. Coast. Eng. 67, 54–66 (2012)

    MATH  Google Scholar 

  45. Tonelli, M., Petti, M.: Hybrid finite volume-finite difference scheme for 2DH improved Boussinesq equations. Coast. Eng. 56(5–6), 609–620 (2009)

    Google Scholar 

  46. Tonelli, M., Petti, M.: Finite volume scheme for the solution of 2D extended Boussinesq equations in the surf zone. Ocean Eng. 37(7), 567–582 (2010)

    Google Scholar 

  47. Tonelli, M., Petti, M.: Simulation of wave breaking over complex bathymetries by a Boussinesq model. J. Hydraul. Res. 49(4), 473–486 (2011)

    Google Scholar 

  48. Tonelli, M., Petti, M.: Shock-capturing boussinesq model for irregular wave propagation. Coast. Eng. 61, 8–19 (2012)

    Google Scholar 

  49. Treske, A.: Undular bores (Favre-waves) in open channels-experimental studies. J. Hydraul. Res. 32(3), 355–370 (1994)

    Google Scholar 

  50. Viviano, A., Musumeci, R.E., Foti, E.: A nonlinear rotational, quasi-2DH, numerical model for spilling wave propagation. Appl. Math. Model. 39(3–4), 1099–1118 (2015)

    MathSciNet  MATH  Google Scholar 

  51. Wei, G., Kirby, J.T., Grilli, S.T., Subramanya, R.: A fully nonlinear Boussinesq model for surface waves. Part 1. Highly nonlinear unsteady waves. J Fluid Mech 294, 71–92 (1995)

    MathSciNet  MATH  Google Scholar 

  52. Zelt, J.: The run-up of nonbreaking and breaking solitary waves. Coast. Eng. 15(3), 205–246 (1991)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mathematics, University of Zurich, Winterthurerstrasse 190, 8057, Zürich, Switzerland

    Paola Bacigaluppi

  2. Team CARDAMOM, Inria Bordeaux Sud-Ouest, 200 avenue de la Vieille Tour, 33405, Talence Cedex, France

    Mario Ricchiuto

  3. University of Bordeaux, CNRS, UMR 5805 EPOC, Allée Geoffroy Saint-Hilaire, 33615, Pessac, France

    Philippe Bonneton

Authors
  1. Paola Bacigaluppi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mario Ricchiuto
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Philippe Bonneton
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Paola Bacigaluppi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bacigaluppi, P., Ricchiuto, M. & Bonneton, P. Implementation and Evaluation of Breaking Detection Criteria for a Hybrid Boussinesq Model. Water Waves 2, 207–241 (2020). https://doi.org/10.1007/s42286-019-00023-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42286-019-00023-8

Keywords

Search

Navigation