Abstract
This paper provides an evolutionary explanation for the different patterns of cooperation across groups in societies in which social and political identity dimensions are cross-cutting, compared to societies in which identity dimensions are overlapping. An agent-based model of interaction between individuals belonging to different groups is presented. An agent’s decision to cooperate or defect in a prisoners' dilemma game is based on the identity of the others along two identity dimensions. In the first version of the model, the two identities are equally salient, while in the second version, their relative salience varies. The results show that in the presence of cross-cutting identity dimensions, cooperation takes place not only within clusters of identical individuals, as suggested by previous models, but also along each of the two identity dimensions, between individuals that share only one of the two identity traits. As the relative salience of one identity dimension increases, cooperating along the lines of the more salient dimension becomes the most successful strategy. These findings are relevant for understanding the patterns of cooperation in heterogenous societies and under increased levels of social and political polarization.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
An extensive political science literature on social cleavages [24, 32, 37], as well as an increasingly large political economy literature on the discrepancy between economic interest and voting behavior [23, 46], suggest that the presence of multiple, cross-cutting identity dimensions changes the patterns of inter-group cooperation, with implications for inter-group coalition formation and political stability. Examples include alliances between different ethnic groups that share an economic interest or alliances between groups that have conflicting economic interests, but have the same preferences over moral issues. At the same time, there is evidence that the relative importance or salience of different identity dimensions has a strong impact on inter-group relations [48, 53, 54].
However, a few attempts have been made to provide formal explanations for the observed relations between multiple intersecting identities and inter-group cooperation, and between the relative salience or relevance of identity dimensions and patterns of social interaction. Axelrod and Hammond [1] and Hammond and Axelrod [26] partially address this issue in their model of local interaction between individuals belonging to different groups. Their main result is that the most successful strategy in this situation is “ethnocentrism”, which is defined as the strategy of collaborating with members of the same group and defecting with members of other groups. Individuals that have a predisposition for in-group favoritism have a better chance of survival and reproduction. Moreover, they conclude that ethnocentrism proves to be a good strategy for sustaining individually costly cooperation in the absence of other more complex mechanisms. However, the groups in Hammond and Axelrod's model are defined on a single identity dimension. In fact, most models of identity and inter-group relations are based on the assumption that individuals have a single activated group identity at a certain point in time.
At the same time, political scientists have long emphasized the multi-dimensional character of social divisions and political competition, which raises several questions: What types of strategies are most successful from an evolutionary perspective in the presence of multiple identity dimensions? Can the observed tendency towards increased cooperation across group lines in situations in which group identities are cross-cutting, as opposed to situations in which the same identities are overlapping be explained? If some of the identity dimensions are more salient than others, how does this relative salience affect the patterns of social interaction? Does it change the success of different evolutionary strategies?
To address these issues, I present a modified version of Hammond and Axelrod’s model, in which there are two identity dimensions present in the population at the same time: color and shape. Each agent is randomly assigned one of four colors: green, red, blue, and yellow and one of four shapes: club, diamond, heart, and spade. Agents then interact with their neighbors in a prisoner’s dilemma game, receive payoffs, and have a chance at local reproduction that is proportional to their accumulated payoffs. Each agent takes its decision to cooperate or defect based on the color and shape of the other, given its own predefined strategy for meeting someone of a certain color and shape. A full set of potential strategies based on combinations of same/different color and same/different shape is defined, and the success of each strategy, as well as the rate of overall cooperation in the world are recorded. Two versions of the model will be analyzed. In the first one, the two dimensions are equally salient. In the second version of the model, I allow for an increase in the salience of one identity dimension relative to the other. Specifically, I focus on a situation in which shape is more important than color and define relative salience as the probability of observing the wrong color while always observing the correct shape of other agents.
The rest of this paper proceeds as follows: The next section presents a brief review of the literature on social identity and inter-group relations, with an emphasis on agent-based models of identity, as well as some insights into the possible effects of multiple identities for group relations, derived from social psychology and the theory of political cleavages. The third section describes the model and the experimental design, and the subsequent one presents and interprets the results. Two aspects are taken into consideration when presenting the results. The first one is a comparison between the original Hammond and Axelrod [26] model and the modified version in which both identity dimensions are equally salient. The second one is a comparison between this equal-salience model specification and the one in which the relative salience of the two dimensions is allowed to vary. The final section summarizes and discusses the findings.
Theoretical motivation
Social identity in agent-based models
Most agent-based models of social identity focus on the endogenous formation and evolution of a sense of shared identity in a population. In Lustick’s [34] model, agents have repertoires of latent identities and decide which of these identities to activate based on the active identities of their neighbors. A curvilinear relation between the size of each agent’s repertoire and the degree of identity concentration in the population emerges. Intermediate repertoire sizes favor the formation of large regions of individuals who share the same identity. Rousseau and Van der Veen [41] discover a similar curvilinear relation between the variety of views in the population and the emergence of shared identity.
Other studies focus less on the emergence and evolution of identity, and more on the political implications of having multiple identities in a population. Epstein [19] models civil violence as a function of the mutual perception by ethnic groups of the others’ right to exist and finds that a peacekeeping central authority is needed to avoid violence and the annihilation of one of the groups. Cederman [8] studies the formation of national identities in ethnically diverse landscapes, while Srbljinovic et al. [47] explain the differences in political mobilization levels across populations through the degree of importance individuals place on their ethnic identity and the structure of the social networks.
Axelrod and Hammond [1] and Hammond and Axelrod [26] develop an agent-based model in which in-group favoritism emerges as the most successful strategy despite being based on arbitrarily assigned group memberships and in the absence of complex cognitive abilities. In their model, agents interact locally in a prisoner’s dilemma game. Each agent has three predefined traits: color, a strategy (defect or cooperate) for meeting someone of the same color, and a strategy for meeting someone of a different color. Ethnocentrism is defined as cooperating with agents of the same color while defecting with others, and in the presence of local interaction and local reproduction, it emerges as the most successful strategy. Maintaining and acting upon a distinctive group identity have been viewed by biologists and social scientists alike as a successful mechanism for overcoming problems of cooperation at the group level. Starting with the experiments of Tajfel [49], people have consistently been found to give preferential treatment to those belonging to their own group, even in situations in which group membership is arbitrarily assigned.
A counter-intuitive result in Axelrod and Hammond [1] and Hammond and Axelrod [26] model is that if ethnocentrism is replaced by a strategy which does not discriminate towards members of other groups, overall cooperation in the world decreases. They also show that the ability to distinguish between in-group and out-group members is essential for maintaining high levels of cooperation in the population and for ethnocentrism to dominate the other possible strategies. Kaznatcheev [29] reaches a similar conclusion. He emphasizes the ability of ethnocentrists to distinguish between in and out-group partners as the main element that separates them from other types of agents, and shows that when a cost of cognition is associated with this ability, ethnocentrism is quickly replaced by humanitarianism (cooperate with everyone) as the most successful strategy.
This suggests that in-group favoritism is best sustained on identity dimensions on which a clear distinction between different categories can be easily made. In fact, one of the main theses of the social identity theory is that in-group favoritism and out-group discrimination can be based on the existence of a shared trait, but only if the trait in question is salient enough in the population [54]. Traits that are not salient tend to be ignored and will not lead to ethnocentrist behaviors. Turner et al. [53] show that increasing the salience of either an induced or preexisting group membership increases in-group favoritism.
A common characteristic of the studies of identity and inter-group relations discussed so far is the presence of a single activated group identity for each individual at a certain point in time. Most of the studies on social identity in the psychology literature are also focusing on a single identity dimension, such as race, ethnicity, class, gender, age, or sexual orientation [28]. When the analysis is extended to two dimensions, one of which is seen as subordinated with respect to the other, the attention is restricted to the individual-level inner conflict between these two dimensions. Examples include studies of the relation between gender and either class [4] or race [39].Footnote 1 However, theories of political competition often assume the existence of multiple identity dimensions along which electorates are divided and political parties compete. These theories are supported by empirical evidence on the positions of voters and parties [5]. The next section discusses the role of multiple identities in the political science literature.
Multiple identity dimensions and political cleavages
Political and social cleavages can be broadly understood as divides between groups in society. For example, an ethnic cleavage—a division between groups with different ethnic backgrounds—could exist in a multiethnic society, or a religious cleavage could exist in a society in which there are multiple religious groups. Depending on their structure and the extent to which they are relevant (or salient) at the societal level, these divisions can have different political and social consequence, can affect the patterns of inter-group interaction and cooperation, and can, in some cases, lead to inter-group conflict.
The term “political cleavage” was coined by Lipset and Rokkan [32], who linked the structure of the party system and the dimensions of political competition that existed in Europe at the time of their writing to the traditional social group divisions which were salient at the beginning of the twentieth century when the European party system was being formed. Social cleavages are based on easily distinguishable social divisions into groups that have a sense of collective identity. The main characteristic that distinguishes political cleavages from other forms of social divisions is the fact that they become institutionalized through the party system. This gives them a high degree of resilience to change. The four primordial political cleavages identified by Lipset and Rokkan [32] were center-periphery, church-state, agricultural-industrial, and the class cleavage. Although this classification is outdated, new, similar divisions have replaced the old ones [2, 30].
When a group that forms a distinctive category on one of these relevant dimensions is equally divided between the multiple categories of another dimension, the cleavages are cross-cutting. The opposite situation is the one in which there is a perfect overlap between the categories of one divide and those of the other (reinforcing cleavages). However, there is an ongoing debate about the correct way of measuring cross-cuttingness. Rae and Taylor [38] propose an index that measures the degree to which two dimensions cross-cut each other, and define it as: “the extent to which individuals who are in the same group on one cleavage are in different groups on the other cleavage”, or, more specifically, the proportion of pairs of individuals whose members are in the same group on one dimension and in another group on the other. Lijphart [33] classifies different cleavage structures based on the angle of intersection of different cleavages. In a recent review of the issue, Selway [43] draws a clear distinction between subgroup fractionalization (defined in a classical manner through the Herfindahl index), cross-cuttingness (which he defines as statistical independence), and what he calls cross-fractionalization (which is Rae and Taylor’s measure).
Regardless of the exact definition, the distinction between cross-cutting and reinforcing cleavages has been used to explain a multitude of observed differences in political outcomes between countries. The main link to be explored was that between the likelihood of having a stable democracy and the existence of cross-cutting political affiliations. The theory is that the importance of each identity dimension is reduced in the presence of cross-cutting ties, which makes conflict less likely and increases the chances for inter-group cooperation [6, 7]. This is an idea that has been present in the political science literature for a long time [15, 16, 40, 45]. If one of the identity dimensions has multiple sub-divisions, the nature of these sub-divisions affects political stability in a similar fashion [9]. Gubler and Selway [25] show that civil war onset is 12 times less probable in societies where ethnicity is cross-cut by other cleavages. Conversely, overlapping cleavages have been generally viewed as a source of conflict [16, 32].
Empirical studies support the idea that the structure of social and political divisions can alter the patterns of inter-group interactions. Dunning and Harrison [18] show that cross-cutting ties stemming from the informal institution of cousinage reduce the political importance of the ethnic dimension in Mali, thus preventing conflict on ethnic lines. At a micro-level, psychologists discovered that adding a second dimension—common values—to a predefined group division affects the behavior of individuals towards members of other groups. Specifically, individuals belonging to a predefined group which is divided on the ideological value dimension discriminate less towards members of other groups [53]. If, however, there is a strong overlap between the values of the individuals and group membership, out-group discrimination is higher. At the same time, political economists have started focusing on the economic effects of social cleavages. Yang [57] and Snowberg [46] tested similar models of cross-cutting cleavages in the context of American politics, by focusing on the impact of the relation between race and income on redistributive policy. They find that at the local level, a looser overlap between race and income has a positive impact on people’s preferences for government spending and redistribution as well as the actual policies that are implemented.
Identity salience and cooperation
The defining characteristic of social cleavages is that they are rooted in sociological divisions based on attributes that are hard to change. Chandra and Boulet [12] define such at- tributes as “ethnic”, while Chandra [10] calls them “sticky”. The divisions that result from such attributes tend to persist for a long time, and, from a constructivist perspective, tend to influence the choice of individuals to identify with one social group or another [42]. Political psychologists make the distinction between salient and non-salient identity attributes, where salience is defined as the likelihood that an identity will be invoked in certain situations [27]. Political scientists, on the other hand, tend to define salience as the likelihood that a certain identity will influence individuals’ behavior and have consequences for political conflict.
Following Tajfel’s [51] theory, Ting-Toomey et al. [52] as well as Espinoza and Garza [20] define salience as the extent to which individuals hold a certain attribute of their identity to be of importance and show that, in laboratory experiments which involve interactions between different ethnic and cultural groups, the patterns of cooperation and conflict are greatly influenced by the extent to which the salience of their ethnic and cultural identity is emphasized. A simple way of increasing the salience of an identity attribute is by manipulating the number of members of the interacting groups. Subjects that are in minority tend to be more aware of their identity and their minority status. Gaertner et al. [22] show that inter-group bias can be reduced by reducing the salience of the identity division, which, in turn, can be achieved through inter-group interaction and cooperative interdependence. Their experiments were based on asking members of different groups to cooperate to solve a task and measuring their bias towards members of the other group afterward. Situations that involved competition between the groups increase the salience of their identities and, as a consequence, increased inter-group bias.
Whether or not different categories of an identity dimension are salient also depends on the social context. Posner [36] shows that a division between two ethnic groups which is salient in Malawi has political consequences that are not present in Zambia, where the same division is not salient. In Malawi, the two ethnic groups form a large share of the country’s population, and political competition becomes structured along the lines of this salient ethnic division. In contrast, in Zambia, where both groups are small and the division between them is not salient, political competition is not structured along the lines of this ethnic division.
Expectations
Previous agent-based models of identity show that within-group cooperation can emerge as a strategy that is successful from an evolutionary perspective. The theories and empirical findings discussed above suggest that in the presence of multiple identity dimensions, the patterns of individual interaction and cooperation will change. The theory of social cleavages makes predictions about the increased likelihood of cooperation across groups that are divided on more than one identity dimension. When social cleavages are cross-cutting, cooperation is expected to take place not only within groups of identical individuals, but also across groups, between individuals that share at least a common identity trait.
Increasing the salience or importance of one social characteristic relative to another makes individuals more aware of the in-group/out-group distinction on the more salient dimension and should, therefore, increase out-group bias on this dimension. Reducing the salience of an identity dimension, on the other hand, should increase the likelihood of cooperation across groups and reduce out-group bias.
The next section shows that these predictions, derived from theories of social identity as well as empirical observation, also emerge from a simple agent-based model of interaction that makes very few assumptions about individual preferences and abilities.
Model description
General setup
The model is a modified version of the Axelrod and Hammond [1] and Hammond and Axelrod [26] model of ethnocentrism, in which there was a single identity dimension. The interesting thing to notice is that a perfectly overlapping (or reinforcing) political cleavage is in fact equivalent to having a single identity dimension. As a consequence, from the perspective of social cleavages theory, Hammond and Axelrod’s model can be seen as a model of perfectly overlapping cleavages. In contrast, the model I develop is a model of perfectly cross-cutting cleavages. Together, these two models provide an agent-based framework for the theory of political cleavages. The extent to which the two dimensions in the model below are cross-cutting is perfect. In Selway’s [43] framework, cross-cuttingness is 1, meaning that the knowing the category an individual belongs to one dimension does not tell us anything about the individual’s position on the other dimension. The two dimensions are independent, and there is a strong tendency for them to remain this way after multiple repeated interactions, when even though the social structure takes a certain shape and some individual strategies outperform others, all the categories on both dimensions are still represented and individuals display a variety of combinations of characteristics.
The model is built in NetLogo, a multi-agent modeling software, and, as already mentioned, it is a modified version of the original model of Axelrod and Hammond [1] and Hammond and Axelrod [26] and the NetLogo version of Wilensky [55, 56]. The space is a toroidalFootnote 2 square lattice of 50 × 50 cells in which each cell can contain a single agent. Two versions of the world setup have been used. In the first one, we start with an empty world in which agents immigrate at a certain rate, while in the second one, we start with a world full of randomly distributed agents. The results are very similar for these two initial setups, so I will report results based on the second one.
Each agent has six traits:
-
One of four colors (red, blue, green, and yellow).
-
One of four shapes (spade, heart, diamond, and club).
-
A strategy (defect or cooperate) for interacting with someone of the same color and same shape.
-
A strategy (defect or cooperate) for interacting with someone of a different color but same shape.
-
A strategy (defect or cooperate) for interacting with someone of the same color but a different shape.
-
A strategy (defect or cooperate) for interacting with someone of a different color and a different shape.
Immigrant agents receive a random combination of these traits, while an offspring of an existent agent takes the traits of its parent, with a small chance of mutation for each trait. The standard case will be that of a rate of immigration of one agent per unit of time and a mutation rate of 0.5% per trait. Agents start with an equal potential to reproduce (PTR), set to 12%. This value changes based on payoffs received by the agents in the prisoner’s dilemma interactions which they have with their neighbor (see the example below). The cost of cooperating with another agent is 1% point and the benefit of receiving help when the other cooperates is 3% points. The resulting prisoner’s dilemma game for these values is presented in Table 1.
For example, cooperating reduces the PTR of an agent from an initial value of 12–11%. Receiving help when the other cooperates increases the PTR of an agent from an initial 12–15%. If both agents cooperate in the one-on-one interaction, assuming that both start with a PTR of 12%, each ends up with a PTR of 14%. The death rate is also equal for all agents, 10%. These parameters were set to the values used by Axelrod and Hammond [1] and Hammond and Axelrod [26] in their simulation to keep the results of their model as a benchmark for comparison.
In the original model, since there was a single identity dimension, agents had two possible strategy traits: one for interacting with someone of the same color and one for meeting someone of a different color. This resulted in four possible combinations of strategies, that defined four genotypes (cosmopolitan—cooperate with everyone; ethnocentrist—cooperate if same color, defect if not; traitor—defect if same color, cooperate if not; and selfish, or defector—defect with everyone). With two dimensions and four strategy traits for each individual, the set of possible combinations of strategies based on both shape and color increases to 16. The resulting 16 genotypes and their behavior are presented in Table 2.
At each time period, the following sequence of stages takes place:
-
a)
First, if there are empty cells in the world, immigrants randomly occupy them at a certain immigration rate.
-
b)
The PTR of each agent is set to the value of the initial PTR. Agents interact with their four von Neumann (immediately adjacent) neighbors in a one-move prisoner’s dilemma in which they decide to cooperate or defect based on their predefined strategies, the color and shape of the other, and the value of a Salience parameter. As a result of these four one-on-one interactions, each agent’s PTR is updated, as described above.
-
c)
Agents have a chance to reproduce which is equal to their updated PTR. Reproduction is asexual and local, meaning that each agent can produce an offspring that shares its features (with a certain chance of mutation) and that the offspring is placed in an empty cell around its parent, if there is one.Footnote 3 The order in which agents are given the chance to reproduce is random.
-
d)
Each agent has a chance of dying equal to the death rate.
Making shape more salient than color
A number of new parameters have been added to the original model. The first and most important one is salience. Salience is defined as importance of one dimension, relative to the other one.
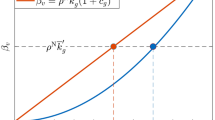
I will capture the notion of identity salience by assuming that the probability of playing a predefined strategy is higher based on shape than based on color. Specifically, I define p as the probability of playing one’s predefined strategy with respect to the shape of the other, and fix it to p = 1. This means that agents will always play their predefined strategy based on the shape of the other. Conversely, I define q as the probability of playing one’s predefined strategy with respect to the color of the other, and let it take several values in the [0.5, 1] interval. When q = 1, always play their predefined strategy with respect to both color and shape. However, when p = 1 and q = 0.8, an agent will always play her predefined strategy with respect to the shape of the other, but will only play the predefined strategy with respect to color 80% of the time. The relative salience parameter is the difference between p and q. (see Table 3).
For example, take the case of an agent who cooperates when meeting the other agents with at least one of same color or same shape, and only defects if the other person shares none of them—a Tolerant (presented in Table 4. Also assume that the Tolerant meets an individual of the same color but a different shape. If the two dimensions were equally salient, the agent would know that the other person has the same color but a different shape, and since only one of these traits is needed for a Tolerant to cooperate, he would have a 100% chance of cooperating. However, if we let Salience = 0.5, this means that the agent has a 50% chance of playing the opposite strategy with respect to color, while still playing her predefined strategy with respect to shape. In this particular situation, upon meeting someone of the same color and a different shape, the agent will have a 50% chance of acting as if he was, in fact, interacting with someone of a different color and a different shape. Since a tolerant is defecting with those that do not share any of his identities, this translates into a 50% chance of defecting instead of cooperating (which is what he would have done if the salience were 0).
The salience parameter is always less than or equal to 0.5, since q ∈ [0.5, 1]. Values of q < 0.5 would simply flip the strategies from defection to cooperation and the other way around on the color dimension while keeping them fixed on the shape dimension. The result would be a mirror image of the world in which q > 0.5. For example, q = 0 would make one always act as if the color of the other was not the same as their own when in reality it is the same, and act as if the color of the other is the same as their own when in reality it is different. This equivalent to the situation in which q = 1, but now, a color-driven agent acts like a color traitor, a color traitor becomes a color-driven agent, and so on. Only the names of the strategies need to be changes, but the model is, in fact, exactly the same as the one in which q = 1.
Operationalizing salience (or relevance) through the extent to which individuals both perceive and, most importantly, act based on the identity characteristics of others is rooted in Lipset and Rokkan’s [32] framework in which social cleavages are formed on easily distinguishable social divisions into groups, which are then institutionalized through the party system. Identity dimensions which have historically and in multiple contexts been identified as most salient are the ones on which it is easy to perceive differences between members of different groups, such as race, ethnicity, and, to some extent, religion. Salience is, therefore, closely linked to perceptions and visibility. In this framework, q = 1 could be interpreted as a perfect ability of the agents to distinguish the color of those they interact with and infer if it is the same as their own or not. The difference p − q would then be the probability that agents will make a mistake about the color of the others.
However, in our model, salience captures more than misperceptions or indeterminacy (the inability to determine the identity of the other)—it captures changes in agent actions. Characteristics may be visible, but individuals may choose not to act based on them. Only when the underlying identity dimension is salient will agents choose to act according to it, and in the model, the action is playing a predefined strategy which is based on the other’s color with a certain probability.
Experimental design
The parameters that were manipulated in the experiments, as well as their values are presented in Table 5. I use grid-sweeping to vary the parameters [31], since their number is not very large and there are naturally arising values for the main parameter of interest (the relative salience of shape is easy to understand as twice as salient, equally salient or 20% more salient). For the other parameters, the purpose was to keep as close as possible to the original configuration of Hammond and Axelrod [26], so we can have a benchmark for comparison.
Since the processes are stochastic processes for which a time average does not provide a representative estimate of variable means, burn-in was established by examining the plots of successful strategies [31]. The process appeared to have entered steady state after 2000 iterations. I, therefore, ran 50 repetitions of 54 model runs corresponding to the combinations of parameters presented in Tables 5 and 6 values for the salience parameter × 3 values for the rate of immigration × 3 values for the rate of mutation × 1 for each of the other parameters—each with 2000 iterations. The variables of interest were recorded at the last iteration. The quantities of interest were computed as ensemble averages. They include: the total number of agents in the world, the number of interactions between different types of agents, the number of cooperative and defective interactions, and the number of agents playing each of the 16 combinations of strategies (genotypes). The standard configuration is similar to the one of Hammond and Axelrod [26], in which there is 1 immigrant per model run and the mutation rate is 0.5% per trait.
Results
Equally salient, cross-cutting identities
This sub-section presents the results of simulations in which the salience parameter is fixed at 0, meaning that both identity dimensions are equally salient. The main question is which of the 16 strategies for interacting with other agents proves to be the most successful in a world where there are two cross-cutting identity dimensions. Figure 1 presents the results for the case in which all the parameters are set at the standard level and the salience is 0. In Hammond and Axelrod’s model, ethnocentrism was defined as cooperating with agents of the same color and defecting with agents of different colors and it was the strategy that ended up dominating almost 75% of the world. Given the wider variety of strategies, here, I redefine Ethnocentrism as the strategy of cooperating only with agents of the same color and shape while defecting with all other types of agents. For example, a Red Heart will only cooperate with other Red Hearts and will defect with everyone else. This strategy is still the most successful from an evolutionary perspective, but its success rate is greatly reduced in the presence of two identity dimensions. Less than a third of the agents in the world are ethnocentrists after 2000 model steps, 19.5% of them are color-driven (cooperate only if they meet someone of the same color) and 19% are shape-driven (cooperate only if they meet someone of the same shape). A t test fails to reject the null that these last two values are equal with 99% confidence.
Moreover, although the difference between the number of ethnocentrists and the number of either shape-driven or color-driven agents is statistically significant, there are worlds in which these two strategies manage to overcome the domination of ethnocentrism. The success of color-driven and shape-driven agents is equal, and the difference between them is not statistically significant. This shows that in the presence of two cross-cutting identity dimensions, individuals that do well are those who cooperate not only with the small group of people who are exactly like them, but also with individuals that share at least one of their traits, without necessarily sharing the other one. From a substantive perspective, this could explain alliances between members of different income groups that have the same ideological preferences. A rich conservative will cooperate not only with other rich conservatives, but also with poor conservatives.
An interesting finding is the success of CDDC agents (who defect with someone of the same shape but not the same color, as well as someone of the same color but not the same shape, but cooperate with both those exactly like them and those that have nothing in common with them). Their performance might be a consequence of their ability to free ride on two of the most highly achieving strategies: color-driven and shape-driven.Footnote 4 Another interesting result is the performance of tolerants—agents who only defect with those of a different color and a different shape—who are the fifth most successful group, with a mean of 9% of the population. Going back to our political economy example, being a tolerant-rich conservative implies a favorable attitude towards other rich people as well as other conservatives, but discrimination towards poor liberals. The element that unites the top most successful strategies is the fact that they all discriminate against individuals who are dissimilar on both identity dimensions.
The fact that the patterns of cooperation are different in a world where there are two cross-cutting identity dimensions does not necessarily mean that the level of overall cooperation in the world will be higher. This result is illustrated in Fig. 2. Overall cooperation is 73.8%, close to the level of overall cooperation reported by Axelrod and Hammond [1] and Hammond and Axelrod [26] for the same combination of parameters but with a single identity dimension. Most of the cooperative interactions take place between agents that share a similar color and a similar shape. This is explained by the social landscape that forms as a consequence of local interaction and local reproduction. Agents tend to form clusters of the same color, same shape, and same strategy (see Fig. 6). However, with greater diversity comes greater potential for defection, which occurs not only at the border between clusters, but also within them, through immigration and mutation. This greater potential for defection would, for instance, be reduced in the case of a null mutation rate, when overall cooperation becomes 83% (see Appendix Fig. 7b).
Low rates of both immigration and mutation favor pure ethnocentrism at the expense of the other, more inclusive strategies.Footnote 5 Color-driven and shape-driven agents perform best at average rates of mutation and relatively low immigration. However, the ranking of the most successful strategies is maintained even at high levels of both mutation and immigration. Tolerants are more affected by changes in the rate of mutation than by increased immigration. This result seems to be driven by the tendency of immigrants to occupy the free cells at the border between two clusters of similar individuals, combined with the greater resilience of tolerants to exploitation at the border than to exploitation from within the group, which matches the previous findings by Shultz et al. [44] with respect to the success of Ethnocentrists in the basic model. Sub-figure b confirms the results of Hammond and Axelrod [26], this time for the two-dimensional case: overall cooperation is negatively affected by increases in mutation and greater immigration. Again, the social landscape helps to explain why this might be the case. As mentioned before, most of the cooperation takes place in clusters of similar agents. The chances of these clusters being weakened from within increase with mutation, while a high number of immigrants affect the clusters at the border. The combination of these two factors has a strong detrimental impact on overall cooperation which only takes place in 60% of the interactions when mutation has a 1% chance of occurring and 10 immigrants enter the world at each unit of time.
Increasing the salience of shape
The previous section has focused on the case of equally important identity dimensions. A more realistic setting is one in which the two identity dimensions have different weights. The importance of one identity dimension versus another can increase or decrease depending on the social and political context or of the moment. For example, an ethnic clash in a neighboring country could increase the salience of the ethnic cleavage at home, while the importance of other identity dimensions remains unchanged or decreases. This section presents the effects of such a change in the relative salience of the two identity dimensions. Figure 3 presents the performance of each strategy when the salience of Shape, relative to color is at its maximum. In this situation, agents are always perfectly capable of observing the shape of the others, but will be wrong about the color 50% of the time.
By far, the most successful strategy is to cooperate as long as the others have the same shape as you but defect if they do not. In the standard case, when immigration is 1 and mutation 0.5%, at the end of 2000 interaction cycles, almost half of the individuals are shape-driven. This shows that if an identity dimension is much more salient than the others, individuals who base their decisions on group membership along that dimension perform best. The second most successful strategy, at a large distance though, is tolerance, with an average of 14.6%, and the third one, with 13.2% of the overall population, is the strategy of cooperating with everyone but those of the same color but not the same shape (CDCC). The success of these two strategies is based on the fact that the first one is rewarding agents that have the same shape, while the second one is punishing those that despite having the same shape do not have the same color. Together, they make good partners for shape-driven agents. Surprisingly, Ethnocentrists perform very badly in such a setup. Only 5.5% of the individuals are playing this strategy. The explanation for this is simple: individuals’ behavior when interacting with others on the non-salient dimension becomes irrelevant. Such interactions do take place (the proportion of different combinations of colors and shapes in the population does not change and all colors and shapes are still present), but they are not relevant for the success of an agent. It is the behavior on the relevant identity dimension that matters. This result is important from a substantive perspective, since it suggests that group divisions which are more visible will tend to dictate the patterns of social interaction and political competition.
The results above reflect the extreme situation in which the relative salience of shape is at its maximum. However, similar conclusions can be drawn for lower values of the difference between the importance of the two identity dimensions. Figure 4 presents the performance of each strategy as salience increases from zero to maximum. The patterns that can be easily observed are: an increased success of shape-driven agents as well as agents that only defect with those of the same color but not the same shape, combined with a decrease in the success of ethnocentrists and color-driven agents. There is, however, no clear trend in the evolution of tolerants as salience increases. Their numbers increase and decrease, and most differences between the mean at one value of salience and the mean at another value are not statistically significant.
We would expect the level of overall cooperation to decrease if one dimension becomes more salient than the other, compared to the situation in which the two identity dimensions were equally salient. Cooperation does seem to go down as the salience of Color decreases, but not by much. Compared to the equally salient identity dimension situation presented in the previous section, the drop in overall cooperation is of 3.2% points. As expected, the difference comes from a decrease in cooperation between agents that are similar on both dimensions, which cannot be compensated by the increase in cooperation between agents that have only shape, but not color in common Fig. 5.
As the number of immigrants increases, the success of shape-driven agents decreases. The same thing happens as the mutation rate increases, and the effects are even more pronounced in this situation. The success of shape-driven individuals is maximal when mutation is zero and immigration is at its minimum. 84% of the agents in the world will be cooperating with those of the same shape and defecting with those of different shape in this situation.
The social landscape
As already mentioned, local interaction and local reproduction favor the formation of clusters of agents of the same shape and color and who are playing a similar strategy. However, the position of these clusters relative to one another varies from one model specification to another. In a model in which color is the only identity dimension, clusters of different colors will be randomly distributed in the space. Adding a second dimension, shape, changes this random distribution. With two, equally important identity dimensions, clusters of agents that share the same color but not the same shape, most of which will be color-driven, will join together and form long regions in which all agents have the same color. At the same time, clusters of agents that have the same shape but not the same color, most of which will be shape-driven, will join together and form long regions in which all agents have the same shape. These two types of long regions will intersect. The intersection spot for two regions will be a cluster of perfectly identical individuals.
Figure 6a presents an example of a world in which shape and color are equally important. The vertical rectangle contains agents of the same color, most of which are either ethnocentrists or color-driven. Since the space is a torus, the triangle continues from the lower right corner to the lower left corner. At the same time, the larger horizontal rectangle that intersects it contains agents of the same shape (spade), most of which are either ethnocentrists or shape-driven. Cooperation occurs along both of these identity regions, and also across them. In contrast, part b of the same figure shows a world in which the relative salience of shape is maximal. Larger regions of the same shape and various colors form here as well, but they are not intersected by other regions in which a certain color dominates, like in the previous case.
To formally test this observed regularity, I conducted 10 repetitions with equal salience and 10 in which shape was twice as salient as color, and used Moran’s I index [14] to make inferences about the spatial distribution of clusters of identical agents on both dimensions. Moran’s index measures the degree to which spatial observations are correlated, and is a measure of the difference between the values of neighboring observations, weighted by the distance between them.
It ranges between − 1 and 1, with 1 corresponding to perfect positive spatial correlation, in which similar values are spatially clustered, 0 to no correlation and − 1 to perfect negative spatial correlation. Chen and Gettis [13] Moran’s I is usually used with continuous variables, and in our case, both color and shape are nominal variables, but since we are interested in the different clustering patterns between the equal-salience model specification and the double shape salience specification, we can create dummy variables for each of the categories of shape (spades, diamonds, hearts, and clubs) and color (red, yellow, green, and blue), compute Moran’s index for each of them, and compare the results. Graphic inspection of the model evolution seems to suggest a high level of correlation for both shape and color subcategories in the equal-salience case, and a somewhat lower level of correlation on the color dimension in case the salience of shape is higher.
Table 6 presents the value of Moran’s I for each of the four categories of the two dimensions independent of each other and averaged over each set of ten iterations. Categories 1–4 correspond to the four possible colors of the agents for the color dimension (red, yellow, green, blue), and the four possible shapes of the agents on the shape dimension (hearts, diamonds, clubs, and spades). The numbers show the degree to which agents that are similar on the specified characteristic (a certain color or a certain shape) are clustered together. As expected, the spatial correlations are on average higher on the shape dimension when shape is more salient than color, but the values are very close to each other when the two dimensions are equally salient.
Robustness checks
Hammond and Axelrod’s results are sensitive to changes in the assumptions made about local interaction and reproduction [3, 29]. The same is valid for this model. Group tags maintain cooperation, but cooperation is contingent upon the proximity between parents and their children. However, assuming that agents interact more with their neighbors and offsprings reside close to their parents, the model passes other robustness tests. Doubling and halving the value of the standard parameters do not change the main results (see Figs. 7a, b, 8a, b, 9, and 10 in the Appendix). Color-driven and shape-driven agents are still among the top three strategies, close to ethnocentrism, and the most successful strategy when the salience of shape is at its maximum is still shape-driven. A similar conclusion was reached for varying the sizes of the groups to half and double the standard values (by changing the probability that an individual with a certain combination of shape and/or color is being born).
Another feature that was added to the model to test its robustness was a cluster variable that takes the value 0 if there are no initial clusters of similar agents and the value 1 if a quarter of the world is initially occupied by agents of the same color and the same shape. This allowed us to test whether spatial clustering affects the results and in what direction. Slightly modified versions of the model included one in which there were more groups on one of the dimensions than on the other and one in which the size of one of the groups, compared to the others was greatly increased. This initial territorial concentration disappeared quickly in interactions and had no effect on the final results. Similarly, there is no distinction between starting with a fully populated world and starting with an empty world or halving and doubling the cost of giving in the game. Despite all these changes, strategies that defect against dissimilar agents perform best, but taken together, the two strategies based on favoritism along identity lines perform better than pure ethnocentrism.
Conclusion
We can summarize the most important results by comparing them to the original model of Hammond and Axelrod [26]. The overall success of color-driven and shape-driven agents which together perform better than Ethnocentrists shows that in the presence of two cross-cutting and equally salient identity dimensions, agents can do well not only by cooperating with the small group of others who are exactly like them, but also by cooperating with agents who share at least one of their traits, without necessarily sharing the other one. However, when the relative salience of Shape is at its maximum, agents who cooperate along the lines of the more salient dimension perform best, outperforming ethnocentrists, as well as all the other strategies by a large margin.
Similarly to the original Axelrod and Hammond [1] and Hammond and Axelrod [26] model, the agent-based model presented here shows that even when group membership is assigned arbitrarily, individuals have very basic cognitive abilities and use very simple strategies for interacting with each other, favoring similar others emerges as the most successful strategy, and the world ends up being populated predominantly by individuals who follow it. At the same time, in the presence of multiple identity dimensions, the most successful strategies match those predicted by social cleavages theory. In societies where social cleavages are reinforcing, cooperation occurs overwhelmingly between members of the same group. However, societies characterized by cross-cutting cleavages achieve cooperation not only within groups of identical individuals, but also between groups of individuals who share one identity feature, but can differ on the other. This result is in accordance to the previous theoretical [21] and empirical studies [6] and [7], which show that peaceful and even cooperative relations between groups are common in contexts in which multiple political and social identities are present.
Situations in which multiple identity dimensions are equally salient in the real world are rare, and most of the time, one dimension is more important than others. The model shows that an identity dimension which has little visibility and small salience becomes irrelevant in inter-group interaction. Such an identity dimension is bound to have little political impact compared to other, more salient dimensions. Therefore, the most successful strategies in this situation are those based on cooperation with similar others along the lines of the more salient identity dimension.
The findings also provide a computational explanation for the ways in which political contexts characterized by marked increases in the salience of an identity dimension relative to others could lead to situations in which cooperation occurs only along the lines of the most salient dimension, at the cost of other forms of cooperation across less salient identity dimension. This results in an overall reduction in levels of cooperation across society and increases the likelihood of inter-group conflict.
A fundamental assumption of the present model is that individuals participate in one-on-one, repeated but isolated encounters. However, according to social identity theory, group behavior and inter-group relations are not just the sum of interactions between separate group members. Taking this fact into account and relaxing the one-on-one interactions, assumption is beyond the scope of this paper but is a promising task for future research.
Notes
See Howard, 2000, for a review of the social psychology literature on identity.
The edges wrap around such that all agents have exactly four adjacent neighbors.
There is no reproduction if all the cells around an agent are occupied. However, the bias that will likely result from this does not run against the results presented. The most successful strategies achieve this status fairly quickly, and the agents playing these strategies tend to form compact clusters that are able to resist invasions even though the individuals in the middle are not able to reproduce.
The baseline percentage driven by the invasion rate, but taking death rate into consideration is 0.66%. Without any interactions but in the presence of migration and mutation there are on average 10 agents in the world at all times. However, migration has a stronger impact in the presence of interactions and in a world dominated by cooperation, since the new agents have the chance to increase their PTR.
References
Axelrod, R., & Hammond, R. A. (2003). The evolution of ethnocentrist behavior. Chicago: Midwest Political Science Convention.
Bartolini, S., & Mair, P. (1990). Identity, competition, and electoral availability: The stabilisation of European electorates 1885–1985. Cambridge: Cambridge University Press
Bausch, A. W. (2014). The geography of ethnocentrism. Journal of Conflict Resolution. https://doi.org/10.1177/0022002713515401.
Beckwith, K. (1998). Collective identities of class and gender: Working-class women in the Pittston coal strike. Political Psychology, 19(1), 147–167.
Benoit, K., & Laver, M. (2006). Party policy in modern democracies. Abingdon: Routledge.
Brewer, M. B. (1997). The social psychology of intergroup relations: Can research inform practice? Journal of Social Issues, 53, 197–211. https://doi.org/10.1111/0022-4537.14199714.
Brewer, M. (2001) Ingroup identification and intergroup conflict: When does ingroup love become outgroup hate? In R. D. Ashmore, L. J. Jussim, & D. Wilder (Eds.), Social identity, intergroup conflict, and conflict reduction (pp. 17–42). Oxford: Oxford University Press US.
Cederman, L.-E. (2002). Endogenizing geopolitical boundaries with agent-based modeling. Proceedings of the National Academy of Sciences of the United States of America, 99(10), 7296–7303.
Chandra, K. (2005). Ethnic parties and democratic stability. Perspect Politics, 3(02), 235–252. https://doi.org/10.1017/S1537592705050188.
Chandra, K. (2006). What Is Ethnic Identity and Does It Matter? Annual Review of Political Science, 9(1), 397–424.
Chandra, K., & Boulet, C. (2003). A model of change in an ethnic demography. Unpublished manuscript, MIT. Retreieved March 3, 2020 from https://www.researchgate.net/profile/Ian_Lustick/publication/228430030_A_model_of_change_in_an_ethnic_demography/links/02bfe514389d0f04b5000000/Amodel-of-change-in-an-ethnic-demography.pdf.
Chandra, K., & Boulet, C. (2012). A combinatorial language for thinking about ethnic identity change. Constructivist theories of ethnic politics, pp. 179–228.
Chen, D., & Getis, A. (1998). Point Pattern Analysis. Working Paper.
Cliff, A. D., & Ord, J. K. (1981). Spatial processes: models & applications. Taylor & Francis.
Dahl, R. (1956). Hierarchy, democracy, and bargaining in politics and economics. In: H. Eulau, S.J. Eldersveld, M.S. Janowitz (Eds.), Political behavior: A reader in theory and research/Ed. Glencoe: Free Press.
Dahl, R. A. (1982). Dilemmas of pluralist democracy: Autonomy vs. control. Yale: Yale University Press.
Dow, J. (2001). A comparative spatial analysis of majoritarian and proportional elections. Electoral Studies, 20(1), 109–125. https://doi.org/10.1016/S0261-3794(99)00041-4.
Dunning, T., & Harrison, L. (2010). Cross-Cutting cleavages and ethnic voting: an experimental study of cousinage in Mali. American Political Science Review, 104(01), 21–39. https://doi.org/10.1017/S0003055409990311.
Epstein, J. M. (2002). Modeling civil violence: An agent-based computational approach. Proceedings of the National Academy of Sciences, 99(90003), 7243–7250. https://doi.org/10.1073/pnas.092080199.
Espinoza, J. A., & Garza, R. T. (1985). Social group salience and interethnic cooperation. Journal of Experimental Social Psychology, 21(4), 380–392. https://doi.org/10.1016/0022-1031(85)90037-X.
Fearon, J. D., & Laitin, D. D. (1996). Explaining interethnic cooperation. The American Political Science Review, 90(4), 715–735.
Gaertner, S. L., Rust, M. C., Dovidio, J. F., & Bachman, B. A. (1996). The contact hypothesis: The role of a common ingroup identity on reducing intergroup bias among majority and minority group members.
Gelman, A. (2008). Red state, blue state, rich state, poor state. Princeton: Princeton University Press.
Goodin, R. E. (1975). Cross-cutting cleavages and social conflict. British Journal of Political Science, 5(04), 516–519. https://doi.org/10.1017/S000712340000836X.
Gubler, J. R., & Selway, J. S. (2012). Horizontal inequality, crosscutting cleavages, and civil war. Journal of Conflict Resolution, 56(2), 206–232.
Hammond, R. A., & Axelrod, R. (2006). The evolution of ethnocentrism. Journal of Conflict Resolution, 50(6), 926–936. https://doi.org/10.1177/0022002706293470.
Hogg, M. A., Terry, D. J., & White, K. M. (1995). A tale of two theories: A critical comparison of identity theory with social identity theory. Social Psychology Quarterly, 58(4), 255–269. https://doi.org/10.2307/2787127.
Howard, J. A. (2000). Social psychology of identities. Annual Review of Sociology, 26(1), 367–393. https://doi.org/10.1146/annurev.soc.26.1.367.
Kaznatcheev, A. (2010). The Cognitive Cost of Ethnocentrism. Presented at the Proceedings of the Thirty-Second Annual Conference of the Cognitive Science Society, Portland.
Kriesi, H. (1998). The transformation of cleavage politics: The 1997 Stein Rokkan lecture. European Journal of Political Research, 33(2), 165–185.
Laver, M., & Sergenti, E. (2011). Party competition: An agent-based model. Princeton University Press.
Lipset, S. M., & Rokkan, S. (1967). Party systems and voter alignments: Cross-national perspectives. New York: Free Press.
Lustick, I. S. (1997). Lijphart, lakatos, and consociationalism. World Politics, 50(1), 88–117.
Lustick, I. (2000). Agent-based modelling of collective identity: Testing constructivist theory. Journal of Artificial Societies and Social Simulation, 3(1), 1–1.
Lustick, I. (2002). PS-I: A user-friendly agent-based modeling platform for testing theories of political identity and political stability. Journal of Artificial Societies and Social Simulation, 5(3), 1–7.
Posner, D. N. (2004). The political salience of cultural difference: Why Chewas and Tumbukas are allies in Zambia and adversaries in Malawi. American Political Science Review, 98(04), 529–545. https://doi.org/10.1017/S0003055404041334.
Powell, G. B. (1976). Political cleavage structure, cross-pressure processes, and partisanship: An empirical test of the theory. American Journal of Political Science, 20(1), 1–23.
Rae, D. W., & Taylor, M. (1970). The analysis of political cleavages. Yale University Press.
Reid, P. T., & Comas-Diaz, L. (1990). Gender and ethnicity: Perspectives on dual status. Sex Roles, 22(7–8), 397–408. https://doi.org/10.1007/BF00288160.
Rose, G. B. (1920). The Industrial Crisis and the Bar. The Virginia Law Register, 6(7), 496–514.
Rousseau, D., & van der Veen, A. M. (2005). The emergence of a shared identity. Journal of Conflict Resolution, 49(5), 686–712. https://doi.org/10.1177/0022002705279336.
Sambanis, N., & Shayo, M. (2013). Social identification and ethnic conflict. American Political Science Review, 107(2), 294–325.
Selway, J. S. (2011). The measurement of cross-cutting cleavages and other multidimensional cleavage structures. Political Analysis, 19(1), 48–65. https://doi.org/10.1093/pan/mpq036.
Shultz, T. R., Hartshorn, M., & Kaznatcheev, A. (2009). Why Is Ethnocentrism More Common Than Humanitarianism? Presented at the Proceedings of the Thirty-First Annual Conference of the Cognitive Science Society, Amsterdam, Netherlands.
Simmel, G. (1964). Conflict and the Web of Group Affiliations. New York, NY: The Free Press.
Snowberg, E. (2007). Cross-Cutting Cleavages and Government Spending. Retrieved March 3, 2020 from http://www.its.caltech.edu/~snowberg/papers/Snowberg%20Cross-Cutting.pdf.
Srbljinovic, A., Penzar, D., Rodik, P., & Kardov, K. (2003). An agent-based model of ethnic mobilisation. Journal of Artificial Societies and Social Simulation, 6(1), 1–1.
Stets, J. E., & Burke, P. J. (2000). Identity theory and social identity theory. Social Psychology Quarterly, 63(3), 224–237.
Tajfel, H. (1970). Experiments in intergroup prejudice. Scientific American, 223, 96–102.
Tajfel, H. (1982). Social psychology of intergroup relations. Annual Review of Psychology, 33(1), 1–39. https://doi.org/10.1146/annurev.ps.33.020182.000245.
Tajfel, H. E. (1978). Differentiation between social groups: Studies in the social psychology of intergroup relations. Academic Press.
Ting-Toomey, S., Yee-Jung, K. K., Shapiro, R. B., Garcia, W., Wright, T. J., & Oetzel, J. G. (2000). Ethnic/cultural identity salience and conflict styles in four US ethnic groups. International Journal of Intercultural Relations, 24(1), 47–81. https://doi.org/10.1016/S0147-1767(99)00023-1.
Turner, J. C., Brown, R. J., & Tajfel, H. (1979). Social comparison and group interest in ingroup favouritism. European Journal of Social Psychology, 9(2), 187–204.
Turner, J. C., & Tajfel, H. (1986). The social identity theory of intergroup behavior. Chicago: Physchology of Intergroup Relations.
Wilensky, U. (1999). NetLogo. Retrieved March 3, 2020, from https://ccl.northwestern.edu/netlogo.
Wilensky, U. (2005). NetLogo Ethnocentrism model. Retrieved March 3, 2020, from https://ccl.northwestern.edu/netlogo/models/Ethnocentrism.
Yang, T.-T. (2003). Cleavage Patterns and Social Conflict: A Theory with an Application to Political Conflict over Fiscal Policy. Retrieved March 3, 2020, from https://eml.berkeley.edu/~webfac/bardhan/e271_f03/yang.pdf.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cioroianu, I. An agent-based model of cooperation with cross-cutting identity dimensions. J Comput Soc Sc 4, 49–75 (2021). https://doi.org/10.1007/s42001-020-00065-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42001-020-00065-w