1 Introduction

Most of the titanium alloys possess significant industrial values owing to their rare and dignified characteristics such as good corrosion resistance, high specific strength, excellent biocompatibility and low weight ratio [1, 2]. Notable industries where this material branch is widely accepted are chemical, gas, oil, power industries, then automobile and aircraft parts manufacturing, and in biomedical application. For all its superior properties, the machinability of Ti alloys is cumbersome due to some of its innate characteristics like retention of high strength even at high temperature and having low Young modulus [3]. Because of the following properties, it is challenging to obtain a good heat dissipation process with direct impact on the increase of the cutting zone temperature.

In this perspective, the use of metalworking fluids (MWFs) in machining of Ti alloys is highly recommended to counterbalance the adversities triggered by this elevated temperature. However, implementation of conventional flood cooling is restricted and to the best case obviated entirely due to the environmental and economic sustainability perspectives. In one side, this limitation and in another side the urgency to ensure congenial machinability of difficult-to-cut (i.e., Ti- and Ni-based alloys) materials have compelled researchers to come up with innovative as well as effective methods of supplying MWFs. Such distinguished techniques are cryogenic cooling, high-pressure cooling, minimum quantity of lubrication (MQL), of cooling and a combination of both cooling/lubrication (MQCL), cooling with compressed air, solid lubricant, nano-fluids and also the hybrid (combination of two or more) methods.

The above strategies have their limitation or benefits; the novel solution made of nano-fluid imported in MQL was studied as an alternative in machining [4, 5]. The nano-fluids are reported to increase the thermal conductivity and heat carrying capacity of MWFs. However, they have small enough to avoid obstruction and abrasion progress. When the nanoparticles are mixed with the fluids for a more extended period of time that facilitate a better heat transfer because the heat transfer will move through the particle’s surface, they can increase the volume fraction of fluid, generating better performances for heat transfer [6, 7].

Numerous research works regarding the machining of Ti alloy have been reported with different advanced techniques for implementing MWFs. For instance, Mia et al. [8, 9] machined the Ti–6Al–4V using a dual oil jet for better chip–tool activity and tool–work interfaces. After the investigations, they reported that the used method had outperformed dry condition; to be specific, reduced tool wear, improved surface finish, lower cutting temperature and force were found. In another study, Mia and Dhar [10] claimed that in machining Ti alloy, an enhanced convective heat transfer by supplied jets divulged favorability in machinability improvement. However, the use of excessive coolant in those studies is against sustainability of manufacturing processes. In that respect, Gupta and Sood [11] reported machining of two difficult-to-cut alloys, i.e., Ti alloy and Inconel grades with the assistance of minimum quantity lubrication. On the other side, Khanna and Sangwan [12]studied the machinability of specific titanium alloys (i.e., Ti–6Al–4V and Ti5553) using an intermittent condition that allows the variation in the edge of cutting tool insert. It was also stressed on the comparative machinability of these two alloys—focusing on the generation of cutting force and temperature. Their study did not utilize any cutting fluids.

Then, Gupta and Sood [13] studied roughness morphology applying turning routine to manufacture Ti (grade II) alloy using the nano-fluid MQL. Besides, they have used desirability-based optimization for multi-objective optimization. Nonetheless, it is essential to study parameters like cutting force and temperature in machining such a material. Liu et al. [14] investigated the cutting force and temperature features under the employment of MQL when Ti–6Al–4V was end-milled. Rahim et al. [15] proposed a natural oil-based lubricant (i.e., Palm oil) using the MQL of Ti–6Al–4V superalloy by simulating high-speed drilling. It was reported that this mode of cooling lubrication outperformed conventional flood cooling and dry condition. Moura et al. [16] used graphite and MoS2 solid lubricants in machining Ti–6Al–4V. That study focused mainly on tool wear, though the authors have studied the surface roughness, temperature and cutting force too. Recently, Ali et al. [17] proved the benefits of machining titanium alloys grade Ti–6Al–4V when were used minimum nano-lubrication that incorporate some surfactant. It is appreciable that quite several research studies have been conducted on machinability of Ti–6Al–4V, but rare studies have considered machining of Ti alloy (grade II).

State of the art highlights the potential of using dry, MQL and nano-fluid assisted by lubricants in a minimum quantity (NFMQL) during machining very challenge materials like various grades of titanium and its alloys. However, the dry machining is not much preferred as it has many adverse effects on the machining performance of titanium and its alloys like material sticking on tool, chips that are not washed, high cutting temperature and poor surface finish, etc. In this respect, the MQL strategy with nano-fluids during turning of titanium and its alloys is considered a viable method toward green or cleaner manufacturing provided the nano-fluid is accredited as environmentally sustainable cooling and lubrication system [5, 18].

Besides, it has been observed from the literature that the proper selection of cutting conditions (i.e., turning parameters, materials of tool together with cooling conditions) requires careful attention that leads to an economic model with the highest productivity, respectively. Thus, the research may be focused on predictive modeling which quantifies and affects the output responses, without performing the experiments. The predictive modeling remains an open area of research, primarily due to the arrival of different novel and improved modeling techniques. Up to now were developed some advanced models using artificial intelligence techniques (algorithms based on neural networks, genetic, neuro-fuzzy techniques and particle swarm optimization) that complement with classical strategy (based on regression-responses prediction). A comparison among the intelligent methods and regression-based modeling was reported in the literature indicating the adaptive neuro-fuzzy inference system (ANFIS) as a more accurate tool [19].

In terms of statistics, the multi-factorial response surface methodology (RSM) provides the best outcomes from the literature studied. The data extracted from experimental results were used for detecting the polynomial coefficients that permit predicting the model outputs. The RSM can be combined with design-of-experiments approach (as per Taguchi strategy) for further improvements. Due to the deficiency of precise analytical models for various machining operations, the experiment-based techniques are gaining more popularity nowadays, and this is exactly what has been done in this paper.

Manufacturing of Ti alloys by machining intrigued many researchers, yet the Ti (grade II) alloy is not studied that much which opens up a window of investigating the machining of this material. Similarly, to effectively plan and control the outcomes of a machining process, prediction of the responses and optimization of the input parameters are inevitable, especially in the face of present resource limitation. Moreover, it is also patent that nano-fluid assistance in machining preserves the potential to improve the machining performances by influencing the thermal and mechanical behavior for critical contacted parts (i.e., interfaces of chip/tool or tool/workpiece).

In this respect, this study intends to reduce the gaps of the literature by studying the turning operation under the implementation of three nano-fluids: aluminum oxide (Al2O3), molybdenum disulfide (MoS2) and graphite (C) with sustainable MQL. Herein, artificial intelligence and statistics based on sophisticated models (i.e., ANFIS and RSM) are utilized to construct a predictive model and an optimization model. The impact of each parameter was detected by applying ANOVA simulation. Afterward, these models are validated with unexplored experimental data. Furthermore, the best nano-fluid is suggested based on the performance criteria (i.e., superior surface roughness, minimum cutting force/temperature). The surface quality for the contacted parts (workpiece and tool surfaces) was observed by scanning electron microscope (SEM).

2 Experimental conditions

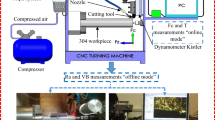
In the experimental work, the material used for turning trials is a Ti (grade II) biocompatible alloy. The machined specimen is 150 mm in length and 50 mm in diameter, respectively. This Ti-grade has application in manufacturing parts such as in automobile industries (i.e., the connecting rods, engine valves, valve spring retainer), for biomedical industries (i.e., the hip and knee joints, bone screws, surgical devices), and for aerospace industries (i.e., the fasteners, castings, gas turbine engines), etc. Details of its chemical composition are shown in Table 1. Specific CBN inserts designed per ISO standards (as CCGW 09T304-2) were employed in the protocol. The inserts geometry is formed from a positive angle of rake 7°, the angle clearance, 80°, rhombic shape, and a radius of nose 0.4 mm. The tool was mounted on the dynamometer of the lathe.

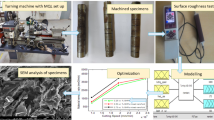
Table 1 Chemical composition of titanium (grade II)
Full size table

Figure 1 presents the experimental setup that contains the CNC turning lathe machine used to perform the oblique turning operations. It is a model “BATLIBOI Sprint 20TC.” By using this setup, a smooth turning process is possible. This machine permits to release a maximum 11 kW for the spindle power, while the speeds of spindle can vary between 30 and 4000 RPM. Each cut was produced for a length of 75 mm, and to produce accurate results, a brand-new insert was embedded.

Fig. 1
figure 1

Experimental setup

Full size image

The nano-fluids were prepared by a two-step method. This process is extensively used in the synthesis of nano-fluids by mixing base fluids with commercially available nano-powders obtained from different mechanical, physical and chemical routes such as milling, grinding and sol–gel and vapor-phase methods. In this method, an ultrasonic vibrator or higher shear mixing device is generally used to stir nano-powders with host fluids. Frequent use of ultrasonication or stirring is required to reduce particle agglomeration. Moreover, stability is a big issue that is inherently related to this operation as the powders easily aggregate due to robust van der Waals force among nanoparticles. Despite such disadvantages, this process is still applicable as the most economical process for nano-fluids production.

The NF-assisted MQL process was developed under a NOGA MQL model. The experiments were conducted using 30 ml/hr (flow rate), 60 L/min (air flow rate) and 5 bar (pressure). In MQL system were used three different nanoparticles, namely aluminum oxide (Al2O3), molybdenum disulfide (MoS2) and graphite (C). They were dispersed uniformly in vegetable oil. The used particles have a maximum size of 40 nm and a concentration of 3% per weight. The morphology of these nanoparticles is shown in Fig. 2. For a homogenous dispersion of the nanoparticles into base oil, an ultrasonicator (for 1 h) and a magnetic stirrer (for half an hour) were used. The nano-fluids viscosity was measured with a rotating viscometer, model: Fungi lab S.A., and the thermal conductivity was evaluated through the hot-wire method using a liquid thermal conductivity instrument, Balaji enterprises; Table 2 presents the achieved value for these properties.

Fig. 2
figure 2

SEM images of nanoparticles: (a) Al2O3, (b) MoS2, (c) graphite

Full size image
Table 2 Properties of nano-fluids
Full size table

The main input cutting parameters studied (i.e., the speed of cutting, feed rate and approach angle) were verified against three nano-fluids (1. Al2O3, 2. MoS2 and 3. graphite) which were selected as input control factors. Further division of the factors into different levels is given in Table 3. The approach angle is also known as the principal cutting-edge angle. It has been taken as a variable for the present study—adjusted to three different values. The approach angle was adjusted by using the provision provided in the TeLC DKM2010 dynamometer. The tool is directly mounted on the lathe tool dynamometer, and the approach angle is adjusted using the adjustable holder, as shown in Fig. 1. Then, the angle is set with the Vernier bevel protector, and the holder is moved as per the respective angle (i.e., 60°, 75°, 90°). Table 3 lists the studied three responses.

Table 3 Input factors and output responses
Full size table

The input parameters were identified based on a robust combination (recommendation from tool manufacturing, state of the art and trial runs). The cutting depth was kept constant (1.0 mm), whereas the speed of cutting along with the feed rate was varied. Here, a depth of cut that is neither too high nor too less (i.e., 1.0 mm) allows desirable strength for the tooltip. At one side, when the tool is used at low cutting depth, its tip experiences contact with the machining surface and subsequently reduces its strength. When a large depth of cut such as more than 1.0 mm is employed, the stress distribution becomes even over the whole edges of tool. So thereby, a prolonged tool life is provided [20, 21].

Moreover, the reference values of depth of cut in ISO 3685 for 0.4 mm nose radius were given as 0.5 mm to 2 mm. An average value (i.e., 1 mm) was selected as per ISO-3685. The specific output responses (i.e., the cutting forces, amount of the tool wear and surface morphology) are dictated vastly by the speed of cutting and feed rate [22].

Surface morphology is linked to feeding rate performances that is translated to the pitch profile as (Ra = f2/32r); here, f represents the feed rate, whereas r is the nose radius of tool. An uncontrolled feed rate produces a sharp increase in surface roughness. A similar mechanism is driven by the cutting forces that govern the formation of uncut chip area and the shear stress (\(F_{c} = A_{c} \times k_{s}\)), where Ac (mm2) denotes the uncut chip area and ks (N/mm2) is the cutting stress. There, the cutting depth has no major effect on the cutting forces performances [20].

The experimental structure was build based on the simulation of Box–Behnken’s RSM (response surface methodology), and the parameters are shown in Table 4. As per the selected design, 29 experiments have been provided by the design of expert software. TeLC DKM2010 dynamometer (Germany) allows acquiring the cutting forces values (Fc) through a linked XKM software. The online cutting temperature (θ) was detected through the HTC infrared thermometer. The acquired values are given in Table 5. Mitutoyo SJ 301 tester was embedded to detect the surface profile in order to determine the average surface roughness parameter (Ra). For all above-mentioned responses, three readings were taken per experimental run and a mean was computed. The mean values of the responses (Fc, θ and Ra) are listed in Table 4.

Table 4 Machining parameters with the experimental design and their results
Full size table
Table 5 The specification of HTC infrared thermometer
Full size table

3 Modeling methodology

3.1 Adaptive neuro-fuzzy inference system (ANFIS)

The fuzzy logic system is endorsed as a good option because it finds immense applications in various fields such as modeling, identification, prediction and measurement. However, the significant limitations of fuzzy systems are that they are not adaptive and the self-learning ability is shallow. On the other hand, the behavior of neural networks is a learning and capable method that permits to generate a relationship between the input-responses parameters. It has been also observed that the neural networks are constructive to solve nonlinear functional problems quickly because it adopts the benefits of both systems, i.e., estimation of input–output data and fuzzy knowledge [23].

Therefore, the ANFIS works as an example that combines the fuzzy and neural systems to identify the predicted parameters. They use the least-squares and hybrid learning rule which incorporate the back-propagation gradient descent methods [24]. The ANFIS network works on the Takagi–Sugeno (TS)-type fuzzy rules (derived from neural learning process). The interference mechanism obeys experimental figures (relation between input parameters and selected responses) or with the system designer experience.

The kth rule is denoted by “If–Then.”

kth rule: If vc is A1 and f is B1, ϕ is C1, and NF is D1, Eq. 1 can be written as:

$$F_{c} = P_{1} \times A_{1} + Q_{1} \times B_{1} + R_{1} \times C_{1} + S_{1} \times D_{1} + T_{1}$$
(1)

where A1, B1, C1 and D1represent fuzzy term sets corresponding to speed of cutting, feeding rate, contact angle and nano-fluid, respectively. P1, Q1, R1, S1 and T1are the adjustable parameters used for tuning the training phase. A total of 29 rules were formulated for selected responses as well. Therefore, in a rule base with k rules (using hybrid training), the ANFIS output can be obtained as in Eq. 2:

$$\begin{aligned} g & = \frac{{w_{1} }}{{\sum\nolimits_{i = 1}^{K} {w_{i} } }}g_{1} + \frac{{w_{2} }}{{\sum\nolimits_{i = 1}^{K} {w_{i} } }}g_{2} + \cdots + \frac{{w_{k} }}{{\sum\nolimits_{i = 1}^{K} {w_{i} } }}g_{k} = \overline{{w_{1} }} g_{1} + \overline{{w_{2} }} g_{2} + \cdots + \overline{{w_{k} }} g_{k} \\ & = (\overline{{w_{1} }} v_{c} )P_{1} + (\overline{{w_{1} }} f)Q_{1} + (\overline{{w_{1} }} \phi )R_{1} + (\overline{{w_{1} }} NF)S_{1} + \overline{{w_{1} }} T_{1} + \cdots + (\overline{{w_{k} }} v_{c} )P_{k} + (\overline{{w_{k} }} f)Q_{k} + (\overline{{w_{k} }} \phi )R_{k} + (\overline{{w_{k} }} NF)S_{k} + \overline{{w_{k} }} T_{k} \\ \end{aligned}$$
(2)

where wi represents the firing strength of ith rule, determined by the second layer of ANFIS.

The three layers with nodes are selected as the ANFIS network structure associated with the cutting forces, the temperature of cutting and surface roughness, respectively [19], giving the nodes functioning process. The mathematical meaning for the ANFIS layers is motivated as:

Layer 1: Each adaptive node that forms a layer can be allocated to a membership grade that corresponds to the input vectors. In this study, the four inputs are associated with a Gaussian membership functions.

Layer 2: Here, the nodes from this dedicated layer allow to calculate the rule of firing strength. The product operator “AND” allows performing this action. Equation 3 describes the firing strength wi obtained from a system with k rules:

$$w_{i} = A(v_{c} )\;{\text{AND}}\;B(f)\;{\text{AND}}\;C(\phi )\;{\text{AND}}\;D({\text{NF}}) = \mu A(v_{c} ) \times \mu B(f) \times \mu C(\phi ) \times \mu D({\text{NF}}),\quad \quad i = 1,2, \ldots ,k$$
(3)

where A(vc), B(f), C(ϕ), D(NF) and μA (vc), μB (f), μC (ɸ), μD (NF) denote the linguistic term set along with the membership functions for the speed of cutting, feed rate, approach angle and nano-fluid, respectively.

Further, a normalized nodes-layer for the firing strength determined for each rule over the sum of the firing strengths of all rules is described by Eq. 4:

$$\overline{{w_{i} }} = \frac{{w_{i} }}{{\sum\nolimits_{i = 1}^{K} {w_{i} } }}.$$
(4)

On layer 2, later phase, each node i is defined by function, expressed in Eq. 5:

$$\overline{{w_{i} }} g_{i} = \overline{{w_{i} }} (P_{i} \times v_{c} + Q_{i} \times f + R_{i} \times \phi + S_{i} \times {\text{NF}} + T_{i} ).$$
(5)

Layer 3: The single node from that layer is computed for the overall output denoted as a sum up to all incoming signals (that obey Eq. 2).

3.2 Response surface methodology (RSM)

Machining industries have a good bonding with response surface methodology (RSM) in terms of its wide application. RSM is a statistical method of three types of modeling: mathematical model, predictive model and optimization model. It works in six functions—(1) input and output variables of a system are to be defined, (2) appropriate experimental design is performed, (3) required regression model development, (4) identification of significant parameters by using analysis of variance, (5) validation of the models by confirmation test and (6) finalization of accept or reject decision.

For this study, (1) inputs are vc, f, ϕ, NF, while outputs are Fc, θ, Ra, (2) Box–Behnken DOE—29 experimental runs, (3) second-order polynomial regression model was developed, (4) ANOVA allows detecting the input parameters that influence the output responses, (5) using explored data, models were validated, and (6) depending on the percentage error the decision was made about acceptance.

The typical form of a first-order model is shown in Eq. 6:

$$y(x) = \beta_{0} + \sum\limits_{i = 0}^{N} {\beta_{i} x_{i} + } \sum\limits_{j = 0}^{N} {\beta_{j} x_{j} + } \sum\limits_{k = 0}^{N} {\beta_{k} x_{k} + \ldots (i,j,k = 1,2,3 \ldots n)}$$
(6)

where \(\beta_{o}\) is the intercept and \(\beta_{1} ,\beta_{2} \ldots \beta_{n}\) are the coefficients of linear terms, respectively, starting from left to right.

3.3 Composite desirability approach

The desirability function approach has been used in this study for generating multi-response optimization of the process parameters. It eliminates the potential of clashing responses in respect of classical optimization strategy. The single response yi (x) is transformed into an individual desirability function (di), yet different of 0 ≤ di ≤ 1. A desirability function can be divided into three categories based on the objective of the response characteristics, mathematically defined in Eqs. 7–9:

First: When the objective is “Higher is better,”

$$d_{i} = \left\{ {\begin{array}{*{20}c} {0,} & {y_{i} \le y_{i*} } \\ {\left[ {\frac{{y_{i} - y_{i*} }}{{y_{i}^{^{\prime}} - y_{i*} }}} \right]^{t} ,} & {y_{i*} < y_{i} < y_{i}^{^{\prime}} } \\ {1,} & {y_{i} \ge y_{i}^{^{\prime}} ,} \\ \end{array} } \right.$$
(7)

where yi* represents the minimum adequate value of yi, yi′ represents the maximum value for the yi, while t denotes the desirability the shape function.

Second: When the objective is “Smaller is better,”

$$d_{i} = \left\{ {\begin{array}{*{20}c} {1,} & {y_{i} \le y_{i}^{^{\prime\prime}} } \\ {\left[ {\frac{{y_{i}^{*} - y_{i} }}{{y_{i}^{*} - y_{i}^{^{\prime\prime}} }}} \right]^{r} ,} & {y_{i}^{^{\prime\prime}} < y_{i} < y_{i}^{*} } \\ {0,} & {y_{i} \ge y_{i}^{*} ,} \\ \end{array} } \right.$$
(8)

where yi″ represents the minimum value of yi, yi* represents the highest adequate value for the i, while r denotes the shape function.

Third: When the objective is “Nominal is better,”

$$d_{i} = \left\{ {\begin{array}{*{20}c} {\left[ {\frac{{y_{i} - y_{i}^{*} }}{{C_{i} - y_{i}^{*} }}} \right]^{s} ,} & {y_{i*} < y_{i} < C_{i} } \\ {\left[ {\frac{{y_{i} - y_{i}^{*} }}{{C_{i} - y_{i}^{*} }}} \right]^{t} ,} & {C_{i} < y_{i} < y_{i}^{*} } \\ {0,} & {y_{i} > y_{i}^{*} \, or \,y_{i*} > y_{i} } \\ \end{array} } \right.$$
(9)

where Ci represents the adequate or objective value, whereas s and t denote the exponential parameters that permit to determine the shape of desirability function. The mathematical desirability function for this multi-response is written as \(D = (d_{i}^{w1} \cdot d_{2}^{w2} \ldots d_{n}^{wn} )\); here, wj (0 < wj < 1) represents the weight value that endorses the jth response importance variable and \(\sum\nolimits_{j = 1}^{n} {w_{j} = 1}\). The best optimum factor is obtained when the combination of these parameters generates the highest desirability. Figure 3 presents a schematic outline of the strategy designed in this survey.

Fig. 3
figure 3

Methodology of the current work

Full size image

4 Results and discussion

The achieved results were discussed in correspondence to the physics of machining. They allow motivating the interaction of the nano-fluids with a tool, chip and workpiece. The predicted and optimized algorithms, along with their verification, were argued.

4.1 Effect of cutting parameter and nano-fluid condition on cutting force

The cutting parameters characteristics developed during machining of titanium (grade II) alloy with direct effects on the cutting force are graphically shown by using the perturbation plot in Fig. 4. In this figure, the speed of cutting is described as the highly dominant factor that drives the cutting force, and the feed rate has a secondary effect while the approaching angle does not affect the process. However, the effect of nano-fluids is essential in reverse order. That is, while the increase of cutting speed increases the value of cutting force, a similar trend in nano-fluids from aluminum to graphite NF the cutting force decreases.

Fig. 4
figure 4

Perturbation plot of cutting force.[A—cutting speed, B—feed rate, C—approaching angle, D—nano-fluid condition]

Full size image

A similar result is also obtainable from the analysis of variance (ANOVA) of cutting force which is listed in Table 6. According to ANOVA principle, if the computed “Prob > F” has a value lower than 0.05, the results are robust. Further, it should meet the condition of “Prob > F” in order to demonstrate the model reliability. A rule of F-test endorses the greater F-values of a specific variable, and the more significant impact on the process performances is developed. Furthermore, there is only 0.01 percent possibility that the “model F-value” is greater than those summed up in Table 6. When the correlation coefficient (R2) is equal to 1, the results are ideal. This following statement helps within explaining the performances of the model fitted by regression analysis. The results from our model for the Fc reach their maximum in terms of R2 that is equal to 1 (Table 6). As per “Pred R-Squared” is also sensibly closer to the “Adj R-Squared,” that further endorse the fitness of the model. Here, the error measurement, i.e., the coefficient of variation (CV) of the developed models, is defined by Eq. 10:

$${\text{CV}} = \frac{{{\text{Std}}.\;{\text{Dev}}.}}{{{\text{Mean}}}}.$$
(10)
Table 6 ANOVA for cutting force
Full size table

The low CV value observed in Table 6 is an indication of the enhanced accuracy and consistency of the experiments conducted. An adequate precision ratio > 4 is desirable. This performance was noted for all simulated models; hence, they are good indicators to validate the simulation. The most significant factors are the speed of cutting and feed rate. Nonetheless, considering the F-value, the speed of cutting is more dominant in defining the cutting force. After these two factors, the nano-fluid plays an essential role in changing the value of cutting force depending on the selection of nano-fluid.

In parallel to the above-mentioned results, a more insightful demonstration of the cutting force behavior is discernible from the 3D plot (see details of Fig. 5a, b). Figure 5a depicts the evolution of cutting forces concerning speed of cutting and feed rate. Moreover, Fig. 5b shows how the cutting forces evolve concerning speed of cutting speed and nano-fluid condition. The increases in speed of cutting and feed rate result in much larger cutting forces.

Fig. 5
figure 5

3D response surface plots: (a) Fc versus vc and f, (b) Fc versus vc and NF

Full size image

Interestingly, the use of different nano-fluids resulted in different values of cutting force. For instance, when the Al2O3 NF was used, the cutting force is higher, compared to the cutting force produced under the use of MoS2 NF, and lastly, the lowest cutting force is found for graphite NF-assisted turning. The use of NF causes a formation of the tribological film, and this film reduces the sliding friction [25]. Also, the used NFs have different values of viscosity and thermal conductivity which resulted in changes in the cutting force. Su et al. [26] had also reported a reduced cutting force when the graphite was used in the oil medium. The lower friction coefficients have been accredited as the possible cause. Similarly, Reddy and Rao [27] claimed that the graphite and MoS2generate lower cutting forces associated with the reduced frictional effect.

The increases in cutting forces with increase in cutting speed and feed rate have driven a larger length of tool–chip contact [28]. The high feed rate can be affected by the geometry of tool (i.e., the nose radius). When the nose radius is more significant, higher stress is developed on the tooltip. Conversely, it can be claimed that the cutting force was increased in such cases. Similarly, the reduction in cutting force with the change in selection of nano-fluids can be imputed to the low viscosity of graphite-based NF.

Furthermore, the use of such NF has facilitated a thin nano-layer at the chip–tool interface. This nano-layer acts as a lubricating layer [29] to cause reduction in the cutting force. Note that this nano-layer also actively aids the cutting fluid (oil) to penetrate to the interfaces at the maximum degree. In support of this fact, Park et al. [29] claimed that NF increases the wet ability of used vegetable oil and reduces friction. A multilayered material like the graphite generates a suitable bonding by a weak van der Waals attraction force between layers. Consequently, this graphite nano-fluid when dispersed suitably produces proper lubrication at nano-size level. Also, the exfoliation process of bulk graphite into few layered graphites allows a better thermal conductivity. There, the ultrasonication engenders the breaking of nanoparticles into even smaller-sized nanoparticles causing the interfaces to be further lubricated and eventually results in a lower cutting force. The effect of NF in aiding material removal has been stressed as micro-machining [30].

4.2 Effect of cutting parameter and nano-fluid condition for the cutting temperature

The perturbation graph with the evolution of cutting temperature during turning of Ti alloy (grade II) by varying the nano-fluids on the MQL conditions is presented in Fig. 6. It is appreciable from this figure that the cutting speed has the highest steepness; therefore, it is the most critical factor in defining the value of the cutting temperature. In other words, the cutting forces increased by a unity could produce the highest magnitude for cutting temperature adjustment. Next to speed of cutting is the evolution of feed rate—it has a moderate slope which indicates a moderate effect on the cutting temperature. Lastly, the nano-fluid condition exhibits that the graphite-based NF, when used in turning, has revealed the lowest cutting temperature. As mentioned in the previous section, a similar trend was found for the cutting force. The classical cutting theory indicates that the cutting force is responsible for generation of cutting temperature due to mechanical work [31]. Thereby, it can be referred that change in cutting forces has caused the change in the local cutting temperature.

Fig. 6
figure 6

Perturbation plot of cutting temperature [A—cutting speed, B—feed rate, C—approaching angle, D—nano-fluid condition]

Full size image

Table 7 presents the ANOVA results for the cutting temperature. In general, the model is significant to a confidence interval of 99%. Moreover, the R2 values indicate that the model is capable of predicting the cutting temperature with good accordance with the experimental cutting temperature. It is further appreciable that only cutting speed is statistically significant. On top of it, the F-value reveals which is highly relevant factor in generating more increase in the local cutting temperature, namely the speed of cutting. After cutting speed, the selection of NFs plays the second most crucial role. However, the feed rate together with the approach angle has negligible contribution.

Table 7 ANOVA for cutting temperature
Full size table

A 3D surface response plotted in Fig. 7 presents the evolution of local cutting temperature concerning the speed of cutting and feed rate/nano-fluid conditions. An augmented speed of cutting and feed rate generate elevation of local temperature (see Fig. 7a). However, as mentioned earlier the rate of change is higher in case of changes of speed cutting as compared to feed rate. Graphite NF revealed the lowest cutting temperature than the Al2O3 and MoS2 NFs.

Fig. 7
figure 7

3D response surface plots: (a) θ versus vc and f, (b) θ versus vc and NF

Full size image

The higher cutting speed means higher momentum of the spindle, which is converted into heat upon the tool–work contact. The heating energy driven by mechanical activity, in turn, produces temperature raises for the tool, work and chip. Hence, the augmentation of speed of cutting generates transformation in the kinetic energy \(\left( {{\text{KE}} = \frac{1}{2}mv_{c}^{2} } \right)\), that is, an increase in produced heat. In this way, thereby, the temperature is increased. Moreover, the relation of cutting speed with temperature increment can be explained by the relation proposed by Cook [32]: \(\Delta \theta = \frac{0.4U}{{\rho C}}\left( {\frac{{v_{c} t_{o} }}{K}} \right)^{1/3}\); here, U is the specific energy, to is the thickness of chip before cut, K represents thermal diffusivity, while ρC denotes the volumetric amount of specific heat. This analytical relation permits creating a proportional relationship between increases of speed of cutting and the local temperature produced in this routine.

The chip–tool contact surface is improved because of using nano-fluid lubrication that decreases considerable friction activity. The friction is reduced by the nano-ball bearing phenomenon of the employed NF between the sliding surfaces. Along with this, the enhanced wetting surface can facilitate improved heat removal [33]. As such, the graphite NF has the lowest viscosity and the highest thermal conductivity (Table 2). The former property assists to generate suitable lubrication activity for the cutting zone, while the following property helps to remove the heat released on the cutting zone. Hence, the excellent performances demonstrated by cutting temperature parameters are attributed to graphite-based nano-fluid that has superior properties.

4.3 Effect of cutting parameter and nano-fluid condition on the surface roughness

The perturbation graph presenting the evolution of surface roughness is depicted in Fig. 8. Here, unlike previous responses, the feed rate is showing the steepest curve. Here, this parameter (i.e., feed rate) proves to be the most critical factor driving the modification of surface roughness. The theory of surface evolution endorses this aspect. Immediately after this parameter, the speed of cutting is shown to have the second most important role. Instead, the approach angle and nano-fluid condition inversely affect the surface roughness. That means the increase in approach angle is associated with superior surface morphology (lower Ra). Also, the graphite-based NF resulted in smoother surface finish.

Fig. 8
figure 8

Perturbation plot of surface roughness [A—cutting speed, B—feed rate, C—approaching angle, D—nano-fluid condition]

Full size image

The quantitative analysis by ANOVA has shown (Table 8) a similar result. Overall, the model is statistically significant. However, the R2 values are little lower than the values found for cutting force and temperature. These R2 values are acceptable as similar results were reported in the literature in predicting the surface roughness by using RSM and other methods. Only significant parameter found in this table is the feed rate. F-value endorses this statement, as the primary importance is played by the feed rate.

Table 8 ANOVA for surface roughness
Full size table

A 3D graph that includes the responses of surface plots associated with the average surface roughness parameter (Ra) is depicted in Fig. 9. A higher feed rate produces a significantly increases for the surface roughness (see details of Fig. 9a). Similarly, the speed of cutting increment is reflected by an increase in surface roughness. In Fig. 9b, the effects of nano-fluid are discernable, though not so prominent, yet the graphite formed by nano-fluid mixture generates the lowest surface roughness. However, it is notable that the generated surface roughness is below 1.0 μm for most of the experimental conditions. This can be attributed to the positive effects of nano-fluids. Mia et al. [8] detected in their study the surface roughness values of Ra mostly higher than 1.0 μm in dry condition. Although they attributed this trend to high-pressure coolant (HPC) system that creates superior surface roughness compared to dry condition, the present study reveals a surface roughness that is even lower than the surface roughness found with HPC assistance in their study.

Fig. 9
figure 9

3D response surface plots: (a) Ra versus vc and f, (b) Ra versus vc and NF

Full size image

In theory, the surface roughness is dictated by the feed rate over the cutting tool nose radius by the relation, \(R_{a} = {\raise0.7ex\hbox{${f^{2} }$} \!\mathord{\left/ {\vphantom {{f^{2} } {32r}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${32r}$}}\). Hence, the nose radius geometry generates alteration on the surface roughness directly proportionally with the feed rate square. They prove our results that the surface roughness suffered higher modification when the feed rate increased. On the other side, the increment of surface roughness caused by a higher speed of cutting is credited to increased vibration with such a high speed of cutting. When machining Ti alloy imposing the speed of cutting higher than 100 m/min pose some issue produced by the inherent characteristics [8,9,10]; this has been already discussed in Introduction section. Here, the cutting speed is 200–300 m/min. Moreover, the large plastic deformations produced at the workpiece interface are locus for chipping initiation; later, the damage can advance forming cracking and tool inserts fracturing that have final effect on surface quality of manufactured part. Figure 10 shows the scanning electron microscopic (SEM) micrographs and 3D surface profiles generated in different nano-fluid-assisted cutting conditions. It is noticeable that depending on the nano-fluid conditions the surface quality varied to a great extent. Figure 10a depicts the machining of Ti alloy (grade II) under Al2O3 nano-fluids at specific cutting conditions. The surface morphology analysis under SEM has underscored feed mark irregularities, adhered microparticles of cutting material and various surface and subsurface layers. It can be summarized that under Al2O3 nano-fluids, machined surface was not perfectly smooth. The reasons can be associated with the longtime stay of the Al2O nano-fluids on the surface of titanium alloy surface. In addition, Fig. 10b highlights the machining of Ti alloy under MoS2 nano-fluids at the same cutting condition to differentiate the surface morphology under lubrication mode. It is pertinent to mention that much smooth surface has been observed under MoS2 nano-fluids compared to Al2O3 nano-fluids, throughout machining. However, small micro-burrs and surface pitting were observed under machining of MoS2 machining. Figure 10c highlights very smooth and clear surface roughness under graphite nano-fluids under the same machining conditions. It is pertinent to mention that very smooth surface with small micro-burrs was observed. However, the surface was smooth under graphite nano-fluids. The surface morphology gets better due to nano-fluid viscosity and sustainability of the graphite nano-fluids at tool–chip interface [30]. In fact, graphite nano-fluids behave perfectly as spacers and effect of ball bearing at tool–workpiece contact interface. Moreover, the wetted area of the NF has reduced by an increase in the contact angle between the workpiece and NF. The used three NFs have a different molecular structure, and reportedly the smaller-sized NFs are more desired as they have the capability for an effective penetration inside the interfaces [34]. Furthermore, an increase in NF concentration causes an increase in the viscosity, yet viscosity that in the system can be altered because of higher local temperature [35].For instance, the nano-fluid when used in suspension with the base oil causes acceleration of heat transfer that facilitates the flush of materials [36, 37]. These phenomena might be the possible cause of the change of the surface.

Fig. 10
figure 10

Machined surfaces corresponding to different working conditions at vc = 300 m/min, f = 0.15 mm/rev, ϕ = 75°: (a, d) Al2O3 nano-fluid, (b, e) MoS2 nano-fluid, (c, f) graphite nano-fluid

Full size image

4.4 Effects of nano-fluids on the tool wear pattern

The influence of different nano-fluids on the evolution of the tool wear was analyzed by SEM technique. Some micrographs with the cutting tool nose, analyzed after machining of Ti alloy using (1) Al2O3-, (2) MoS2-, and (3) graphite-assisted MQL, are presented in Fig. 11. Figure 11a depicts the primary cutting-edge fracture and eventual damage of the tool edge. This can be explained by the fact that when the Al2O3 particles have been impinged between the tool and work, the hard Al2O3 nanoparticle might have worked as the agent for crack initiator on the tool surface. Later this crack might have propagated by the tool imposed cutting stress and eventually caused the tool’s outer layer to be failed. Similarly, Fig. 11b underscores the nose wear and coating spelling under machining of MoS2 nano-fluids. However, it did not reveal any such severe tool material breakage from the nose area as previously under Al2O3 nano-fluids. Instead, it is observable that the tool rake face has ensured severe abrasion. The rake surface presents some abrasion mark (see Fig. 11c) under machining of graphite nano-fluids. However, overall a smoother tool profile that has little adhesion of material is displayed. The reduced wear process was demonstrated on the tool, when the graphite-MQL strategy was developed, for manufacturing of Ti alloy, is associated with a better lubrication mechanism and low hardness. In addition, the lowest viscosity of graphite enabled a smoother movement of the tool edge over the work surface. In that condition, the tribological behavior was improved locally and consequently produced a better surface of the tool.

Fig. 11
figure 11

Tool wear images at different working conditions at vc = 300 m/min, f = 0.15 mm/rev, ϕ = 75°: (a) Al2O3 nano-fluid, (b) MoS2 nano-fluid, (c) graphite nano-fluid

Full size image

4.5 Prediction by ANFIS

Adaptive neuro-fuzzy inference system (ANFIS) was simulated to reduce the cutting force/temperature and improve surface roughness. Here, in Figs. 12, 13 and 14, the experimentation scheme and designed ANFIS architecture, fuzzy model structure and rule viewer of the training process for cutting force predictive modeling are presented, respectively. The similar structure was developed to detect suitable cutting temperature while improving the surface roughness values, which is not presented here. Data that were generated in this process (input vs. output) are used to design the training data set (similar as the polynomial model used in RSM) in the ANFIS system, and the prediction model is developed using the technical specification already discussed in Sect. 3.1. Then, to check the validity of proposed models 10 experiments (different from training data set) were carried out. Before doing so, the response values of these experiments are collected and listed in Table 9. Afterward, the values of input variable were put into the ANFIS model rule viewer, and the corresponding output was computed. In this manner, all the responses corresponding to the testing runs were computed and are listed in Table 9 under the column “pre-ANFIS.” It shows that the experimental value and ANFIS predicted values of Fc, θ and Ra show a good agreement. In fact, the absolute percentage errors for these responses were 3%, 5% and 4%, respectively.

Fig. 12
figure 12

Experimentation scheme and designed ANFIS architecture for cutting force prediction

Full size image
Fig. 13
figure 13

Fuzzy model corresponding to cutting force

Full size image
Fig. 14
figure 14

Rule viewer of fuzzy model

Full size image
Table 9 Predicted RSM, ANFIS and experimentally obtained values for turning operation
Full size table

4.6 Mathematical model by RSM

As mentioned earlier, in Sect. 3.2, the RSM regression analysis method was built considering three mathematical models that include parameters for cutting forces, local cutting temperature together with surface roughness. Afterward, those models are validated with a testing data set (unused in training the model). The designed polynomial models for the prediction of cutting forces, local cutting temperature together with surface roughness were provided within Eqs. 11–13:

$$F_{c} = 57.96552 + 0.62667v_{c} + 513.3333f + 0.22222\phi - 9.16667{\text{NF}}$$
(11)
$$\theta = 257.54023 + 0.90500v_{c} + 253.3333f - 0.0611\phi - 5.50{\text{NF}}$$
(12)
$$R_{a} = 0.23511 + 2.01667 \times 10^{ - 3} v_{c} + 3.13333f - 3.27778 \times 10^{ - 3} \phi - 0.035NF.$$
(13)

The R2 values of these models are 92%, 90% and 74% proving higher model performances. The complete details of RSM predicted values are presented in Table 9, values that belong to column “pre-RSM.” There, the simulated and experimental testing values are in good agreement to each other which justify the acceptability of these models; this phenomenon is also visible in Fig. 15—correlation plot of predicted and experimental values of cutting force.

Fig. 15
figure 15

Correlation between experimental and RSM predicted cutting forces for testing data set

Full size image

4.7 Comparison of ANFIS and RSM models

The comparison of RSM and ANFIS modeling has been made, and the predicted values are graphically presented in Fig. 16a–c. The main parameters verified were the cutting forces/ temperature and details of surface roughness. It has been found that the results are more accurately predicted in the case of ANFIS model. Besides, a numerical comparison was performed based on the minimum value of the absolute percentage error (APE) which is calculated using Eq. 14 and listed in Table 9:

$${\text{APE}} = \frac{{\left| {{\text{Actual}} - {\text{Predicted}}} \right|}}{{{\text{Actual}}}} \times 100.$$
(14)
Fig. 16
figure 16

Deviation plots

Full size image

It is observable from Table 9 that the APE for any model is less than 10%—it indicates that all the developed models are highly accurate. In fact, in many cases the APE is less than 1%. If compared with RSM, the ANFIS models exhibited a better accuracy in terms of a lower APE value. The mean absolute percentage error (MAPE) was also computed using Eq. 15:

$${\text{MAPE}} = \frac{1}{N}\sum\limits_{n = 1}^{N} {\left( {\frac{{\left| {{\text{Actual}} - {\text{Predicted}}} \right|}}{{{\text{Actual}}}}} \right)} \times 100.$$
(15)

The determination of ANFIS models for the main parameters (i.e., cutting force, local cutting temperature and surface roughness) generates the MAPE values 1.888%, 0.405% and 1.645%, while those for the RSM models are 3.434%, 1.164% and 4.072% successively for the respective responses. Therefore, an obvious conclusion is that the ANFIS model outperforms the RSM model. In other words, the ANFIS demonstrates a better convergence toward experimental outcomes compared to the RSM approach in predicting these three main parameters (i.e., cutting force, local cutting temperature and surface roughness) on turning operation. Notwithstanding, the ANFIS requires a better quality of the training data. Besides, it depends extensively on the empirical calculation that allows identifying suitable structure that reflects a better current condition. The RSM that is based on statistical determination appears as a more robust method when training data space is available.

4.8 Optimization by CDA

Based on the fundamental of composite desirability approach (CDA) described in Sect. 3.3, in this section, the cutting force/temperature and surface roughness were optimized applying an objective of “minimization” for all the responses. However, in doing so, all the input parameters were varied in a controlled way within the range of the input values. For instance, the speed of cutting speed was used within a range of 200 m/min to 300 m/min. Similarly, other input parameters, outputs, their range, weights and essential follow the range given in Table 10.

Table 10 Inputs and outputs with respective weight and importance for desirability-based optimization
Full size table

Here, an equivalent weight (= 3) is assigned to cutting force, temperature and roughness. This assumption was used due to high significance for all the responses that contributed to the manufactured performances of a part. For instance, the cutting force acts predominantly for the deformation of the structural component of a machine tool. Furthermore, the dimensional deviation and tolerance alteration are influenced by the changes in the cutting force. Likewise, the surface roughness parameters have been known to affect the dimensional accuracy, fitting of product-pair, surface morphology, residual stress and its key engineering performance. On the other side, the cutting temperature highly influences the tool–work interface. Thereby, the tool performance, as well as the machined surface quality, is adversely affected.

The results of the optimization are shown in Table 11 along with other close iterations. Furthermore, the ramp function graphs for variable with best combinations are plotted in Fig. 17. A suitable condition is encountered when Vc = 200 m/min, f = 0.1 mm/rev, ϕ = 79.83 and graphite NF is used. At these parameter sets, the composite desirability was 0.9501 (where 1.0 is ideal condition). The optimum results found in this method were as follows: Fc = 108.99 N, θ = 442.52 °C and Ra = 0.5854 µm. Therefore, the best solution is obtained with the lowest value of speed of cutting/feed rate, average value of approach angle and using the graphite-based nano-fluid.

Table 11 Optimum values of the parameters with maximum desirability
Full size table
Fig. 17
figure 17

Ramp function graph for optimized values

Full size image

5 Conclusion

This research deals with the machinability of Ti (grade II) alloy submitted to a turning process using CBN cutting tool. The impingement of nano-fluid-assisted MQL was investigated to attain better control of the cutting forces, temperature and surface roughness. Moreover, performance prediction together with optimization models was developed using statistical and intelligent methods. Besides, the effects of exploited parameters are determined. Finally, the optimum control factor levels and the best performing nano-fluid are suggested. Concluding remarks are as follows:

  • Among the investigated nano-fluids (Al2O3, MoS2, C), graphite NF showed best features that allow decreasing the cutting force and temperature and improving surface roughness. A better tool profile of the worn insert was found for graphite-assisted MQL too. This can be attributed to graphite’s layered structure which provides sufficient lubrication and to the higher thermal conductivity which efficiently removes heat from cutting zone.

  • The speed of cutting exhibited a most considerable influence on the cutting force and local temperature, while the feed rate influenced the surface roughness primarily. This can be accredited to increased kinetic energy and chip–tool contact length by augmentation of the speed of cutting. Yet, an increased feed rate creates an increased distance between the ridges of turning curvilinear profile.

  • The developed predictive models are proven accurate and reliable based on the appropriate statistical error assessment. The average absolute errors detected, for the RSM models, of Fc, θ and Ra, were found to be ~ 14%, ~ 18% and ~ 20%, respectively, whereas the errors for ANFIS models were ~ 3%, ~ 5% and ~ 5%, respectively. This indicates that ANFIS demonstrates better convergence toward experimental outcomes compared to RSM approach due to its ability to create a more robust relationship of input parameters. These models can help in establishing the manufacturing system with automatic controlling of turning parameter.

  • The mathematical models showed a high degree of accuracy in terms of higher correlation coefficient (R2 → 1). The optimum parameter levels are vc = 200 m/min, f = 0.1 mm/rev, ϕ = 79.83, and graphite NF condition. At these parameter levels, the composite desirability was 0.9501 and responses were Fc = 108.99 N, θ = 442.52 °C and Ra = 0.5854 µm.

6 Future scope

Some tentative future avenues of research can be the investigation of other nano-fluids by simulating machining process using different metals and alloys, with keen focus on superalloys machining. Besides, other modeling techniques based on artificial intelligence (AI) can further generate more accurate models for improving machining parameters (i.e., cutting force, local temperature, surface roughness, tool wear, tool life, etc.).