Abstract
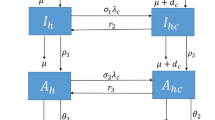
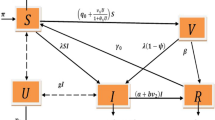
Acquired immunodeficiency syndrome (AIDS) is an infectious and contagious disease caused by the human immunodeficiency virus (HIV), which is a global health problem. This study presents a cellular automaton (CA) model of HIV that uses an adaptation of the system of ordinary differential equations proposed by Anderson et al. (J Math Appl Med Biol 3:229–263, 1986) and an interval type-2 fuzzy rule-based system (FRBS). The aim of this study is to show that this CA model is consistent with known statistical results of HIV patients. The novelty of this research is not only the use of CA with a type-2 FRBS to model the HIV in a way that is consistent with the data, its adaptation and improvement of the standard dynamical system model of Anderson et al. (J Math Appl Med Biol 3:229–263, 1986) by adding three phases of viral evolution of the HIV infection in the absence of antiretroviral treatment. One of the features of the CA is its randomness due to the movement of its cells, the infection period in which the individuals are, the places and partners that represent the activity of the HIV population. This feature is efficiently modeled using FRBS with interval type-2 fuzzy sets. The output of our model favorably compares to the data from the period of 1980–1995, when the use of antiretroviral drug was not available.



















Similar content being viewed by others
References
Anderson RM, Medley GF, May RM, Johnson A (1986) A preliminary study of the transmission dynamics of the human immunodeficiency virus HIV, the causative agent of AIDS. IMA J Math Appl Med Biol 3:229–263
AVERT (2015) Worldwide HIV & AIDS statistics. http://www.avert.org/worldwide-hiv-aids-statistics.htm. Accessed May 2015
Benyoussef A, HafidAllah NE, ElKenz A, Ez-Zahraouy H, Loulidi M (2003) Dynamics of HIV infection on 2D cellular automata. Phys A 322:506–520
Cabrera N (2014) Aplicação da extensão de Zadeh para conjuntos fuzzy do tipo 2 intervalar. Master’s thesis, Universidade Federal de Uberlândia, Uberlândia, Brazil (in Portuguese)
Castillo O, Melin P (2008) Type-2 fuzzy logic: theory and applications. Springer, Berlin
Coutinho FAB, Lopez L, Burattini M, Massad E (2001) Modelling the natural history of HIV infection in individuals and its epidemiological implications. Bull Math Biol 63:1041–1062
Czaran T (1998) Spatiotemporal models of population and community dynamics. Chapman & Hall, Boca Raton
Ermentrout G, Edelstein-Keshet L (1993) Cellular automata approaches to biological modeling. J Theor Biol 160:97–133
Golpayegani GN, Jafari AH, Dabanloo NJ (2017) Providing a therapeutic scheduling for HIV infected individuals with genetic algorithms using a cellular automata model of HIV infection in the peripheral blood stream. J Biomed Sci Eng 10:77–106
Gomes L, Barros L, Bede B (2015) Fuzzy differential equations in various approaches. Springer Briefs in Mathematics, Berlin
Gruttola V, Seage G, Mayer K, Horsburgh C (1989) Infectiousness of HIV between male homosexual partners. J Clin Epidemiol 42(9):849–856
Health M (2012) Aspectos clínicos do HIV e boletim epidemiológico AIDS.DST. http://www.aids.gov.br. Accessed 25 May 2012 (in Portuguese)
Jafelice RM, Silva CAF, Barros LC, Bassanezi RC (2015) A fuzzy delay approach for HIV dynamics using a cellular automaton. J Appl Math 2015:378753. https://doi.org/10.1155/2015/378753
Jafelice R, Barros L, Bassanezi R, Gomide F (2004) Fuzzy modeling in asymptomatic HIV virus infected population. Bull Math Biol 66:1463–1942
Jafelice RM, Bechara BFZ, Barros LC, Bassanezi RC, Gomide F (2009) Cellular automata with fuzzy parameters in microscopic study of positive HIV individuals. Math Comput Model 50:32–44
Jafelice RM, Barros LC, Bassanezi RC (2014) Study of the dynamics of HIV under treatment considering fuzzy delay. Comput Appl Math 33:45–61
Jafelice R, Silva P (2011) Cellular automata—simplicity behind complexity, Intech, chap studies on population dynamics using cellular automata, pp 105–130
Karnik N, Mendel J, Liang Q (1999) Type-2 fuzzy logic systems. IEEE Trans Fuzzy Syst 7(6):643–658
Lee Y, Kouvroukoglou S, McIntire L, Zygourakis K (1995) A cellular automaton model for the proliferation of migrating contact-inhibited cells. Biophys J 69:1284–1298
Mendel J (2007) A reprint “type-2 set and systems: an overview”. Suppl IEEE Comput Intell Mag 2(1):20–29
Mendel J, Wu H (2007) New results about the centroid of an interval type-2 fuzzy set, including the centroid of a fuzzy granule. Inf Sci 177:360–377
Mendel J, John R, Liu F (2006) Interval type-2 fuzzy logic systems made simple. IEEE Trans Fuzzy Syst 14(6):808–821
Mendel JM, Rajati MR, Sussner P (2016) On clarifying some definitions and notations used for type-2 fuzzy sets as well as some recommended changes. Inf Sci 340–341:337–345
Mielke A, Pandey R (1998) A computer simulation study of cell population in a fuzzy interaction model for mutating HIV. Phys A 251:430–438
Moore EF (1962) Machine models of self-reproduction. In: Proceddings of symposia in applied mathematics, United States of America, vol XIV, pp 17–34
Mostafa K, Khalid H, Noura Y (2014) Modeling the adaptive immune response in HIV infection using a cellular automata. Int J Eng Comput Sci 3:5040–5045
O’Brien T, Shaffer N, Jaffe H (1995) Transmissão e infecção do vírus HIV. In: Sande M, Volberding P (eds) Tratamento Clínico da AIDS, 3rd edn. Revinter, Rio de Janeiro, pp 3–14 (in Portuguese)
Pedrycz W, Gomide F (1998) An introduction to fuzzy sets: analysis and design. MIT, Cambridge
Perelson A, Nelson P (1999) Mathematical analysis of HIV-1 dynamics in vivo. SIAM Rev 41:3–44
Rachid M, Schechter M (2005) Manual de HIV/AIDS, 8th edn. REVINTER, Rio de Janeiro (in Portuguese)
Renning C (1999/2000) Collective behaviour: Emergent dynamics in populations of interacting agents. In: Seminar artificial life
Rizol PR, Mesquita L, Saotome O (2011) Lógica fuzzy tipo 2. Revista SODEBRAS 6:27–46
Saag M (1995) Diagnóstico laboratorial da AIDS presente e futuro. In: Sande M, Volberding P (eds) Tratamento Clínico da AIDS, 3rd edn. Revinter, Rio de janeiro, pp 27–43 (in Portuguese)
Santos R, Coutinho S (2001) Dynamics of HIV infection: a cellular automata approach. Phys Rev Lett 87(16):1681021–1681024
Silva C, Jafelice R (2010) Uso de autômato celular em tratamento dos HIV positivos dependendo da evolução da doença. In: \(18^{\circ }\) SIICUSP, São Paulo, Brazil (in Portuguese)
Sloot P, Chen F, Boucher C (2002) Cellular automata model of drug therapy for HIV infection. In: Lecture notes in computer science, pp 282–293
UNAIDS (2013) http://www.unaids.org. Accessed Oct 2014 (in Portuguese)
Wolfram S (1994) Cellular automata and complexity. Addison-Wesley publishing Company, New York
Zadeh L (1965) Fuzzy sets. Inf Control 8:338–353
Acknowledgements
The first author acknowledges to the Brazilian Research Agency CAPES for the scholarship process number 88881.119095/2016-01. The fourth author acknowledges CNPq, the Brazilian National Research Council, for its financial support (process 305862/2013-8).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Eduardo Souza de Cursi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Jafelice, R.M., Pereira, B.L., Bertone, A.M.A. et al. An epidemiological model for HIV infection in a population using type-2 fuzzy sets and cellular automaton . Comp. Appl. Math. 38, 141 (2019). https://doi.org/10.1007/s40314-019-0867-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-019-0867-8