Dynamic maximal covering location problem for fire stations under uncertainty: soft-computing approaches | International Journal of System Assurance Engineering and Management Skip to main content
Springer Nature Link
Log in

Dynamic maximal covering location problem for fire stations under uncertainty: soft-computing approaches

  • Original Article
  • Published:
International Journal of System Assurance Engineering and Management Aims and scope Submit manuscript

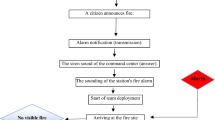
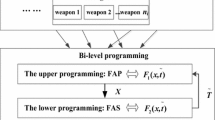
Abstract

In this paper, a mathematical formulation is presented for fire station’s locating and facilities allocating to stations in different periods and emergency situations (wars and natural disasters). This model is designed, considering amount of demands and facilities coverage radius, being dynamic based on traffic and type region and fuzzy in different periods. According to fact, in the model, amount of demand for each demand point depends on number of coverage and the location. In this model, location of stations is positioned once in different periods. The number of facilities which are allocated to stations are located dynamically and can be relocated in different periods. Since the proposed model is NP-hard, particle swarm optimization (PSO) and artificial bee colony (ABC) algorithms by considering an efficient combinatorial chromosome are presented to solve the problem at hand. In the PSO, way of making chromosome is such that locating chromosome, early and final allocation are presented in a novel approach. The results demonstrated that the presented PSO are better than ABC in terms of quality of solutions and computational time.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  • Afzal S, Padmanabh T (2017) Reduced order modelling of linear time invariant system using modified cuckoo search algorithm. Soft Comput 22:3449–3459

    Google Scholar 

  • Afzal S, Rajendra P (2017) New technique for system simplification using cuckoo search and ESA. Sadhana 42:1453–1458

    MathSciNet  MATH  Google Scholar 

  • Araz C, Selim H, Ozkarahan I (2007) A fuzzy multi-objective covering-based vehicle location model for emergency services. Comput Oper Res 34:705–726

    MATH  Google Scholar 

  • Aytug H, Saydam C (2002) Solving large-scale maximum expected covering location problems by genetic algorithms: a comparative study. Eur J Oper Res 141:480–494

    MathSciNet  MATH  Google Scholar 

  • Barbas J, Marin Á (2004) Maximal covering code multiplexing access telecommunication networks. Eur J Oper Res 159:219–238

    MathSciNet  MATH  Google Scholar 

  • Basar A, Çaray B, Ünuyurtt T (2011) A multi-period double coverage approach for locating the emergency medical service stations in Istanbul. J Oper Res Soc 62:627–637

    Google Scholar 

  • Batanovic V, Petrovic D, Petrovic R (2009) Fuzzy logic based algorithms for maximum covering location problems. Inf Sci 179:120–129

    MATH  Google Scholar 

  • Berman O, Huang R (2008) The minimum weighted covering location problem with distance constraints. Comput Oper Res 35:356–372

    MathSciNet  MATH  Google Scholar 

  • Berman O, Krass D (2002) The generalized maximal covering location problem. Comput Oper Res 29:563–581

    MathSciNet  MATH  Google Scholar 

  • Berman O, Wang J (2011) The minmax regret gradual covering location problem on a network with incomplete information of demand weights. Eur J Oper Res 208:233–238

    MathSciNet  MATH  Google Scholar 

  • Berman O, Krass D, Menezes MBC (2007) Facility reliability issues in network p-median problems: strategic centralization and co-location effects. Oper Res 55:332–350

    MathSciNet  MATH  Google Scholar 

  • Berman O, Drezner Z, Wesolowky GO (2009) The maximal covering problem with some negative weights. Geogr Anal 41:30–42

    Google Scholar 

  • Bhatt R, Parmar G, Gupta R, Sikander A (2018) Application of stochastic fractal search in approximation and control of LTI systems, Microsystem Technologies pp 1–10.

  • Canbolat MS, Vonmassow M (2009) Planar maximal covering with ellipses. Comput Ind Eng 57:201–208

    Google Scholar 

  • Colombo F, Cordone R, Lulli G (2016) The multimode covering location problem. Comput Oper Res 67:25–33

    MathSciNet  MATH  Google Scholar 

  • Curtin KM, Hayslett-Mccall K, Qie F (2010) Determining optimal police patrol areas with maximal covering and backup covering location models. Netw Spat Econ 10:125–145

    MathSciNet  MATH  Google Scholar 

  • De Assis CF, Lorena LAN, Ribeiro GM (2009) A decomposition approach for the probabilistic maximal covering location-allocation problem. Comput Oper Res 36:2729–2739

    MathSciNet  MATH  Google Scholar 

  • Eberhart R, Kennedy J (1995) A New Optimizer Using Particle Swarm Theory, In: Proceedings of the sixth international symposium on machine and human science, pp 39–43.

  • Erdemir ET, Battar SS, Rogerson PA, Blatt A, Flanigan M (2008) Location coverage models with demand originating from nodes and paths: application to cellular network design. Eur J Oper Res 190:610–632

    MathSciNet  MATH  Google Scholar 

  • Espejo LGA, Galvao RD, Boffey B (2003) Dual-based heuristics for a hierarchical covering location problem. Comput Oper Res 30:165–180

    MATH  Google Scholar 

  • Fajardo Calderín J, Nodarse CP, Year LS, Diago E, Rodrígue E (2017) Software tool for model and solve the maximum coverage location problem a case study: location police officers. Revista Invest Oper 2:141–149

    MathSciNet  Google Scholar 

  • Farahanir Z, Hassani A, Mousavis M, Bayagi MB (2014) A hybrid artificial bee colony for disruption in a hierarchical maximal covering location problem. Comput Ind Eng 75:129–141

    Google Scholar 

  • Galvao RD, Espejo LGA, Boffey B (2000a) A comparison of Lagrangean and surrogate relaxations for the maximal covering location problem. Eur J Oper Res 124:377–389

    MathSciNet  MATH  Google Scholar 

  • Galvao RD, Gonzalo AcostaC Espejo L, Boffey B (2000b) A comparison of Lagrangean and surrogate relaxations for the maximal covering location problem. Eur J Oper Res 124:377–389

    MathSciNet  MATH  Google Scholar 

  • Galvao RD, Espejo LGA, Boffeyb B (2002) A hierarchical model for the location of perinatal facilities in the municipality of Rio de Janeiro. Eur J Oper Res 138:495–517

    MathSciNet  MATH  Google Scholar 

  • Gendreau M, Laporte G, Semet F (2001) A dynamic model and parallel tabu search heuristic for real-time ambulance relocation. Parallel Comput 27:1641–1653

    MATH  Google Scholar 

  • Gumawarane G (1982) Dynamic versions of set covering type public facility location problems. Eur J Oper Res 10:190–195

    Google Scholar 

  • Hajipour V, Zanjiranifarahani R, Fattahi P (2016) Bi-objective vibration damping optimization for congested location-pricing problem. Comput Oper Res 70:87–100

    MathSciNet  MATH  Google Scholar 

  • Hasanzadeh H, Bashiri M, Amiri A (2018) A new approach to optimize a hub covering location problem with a queue estimation component using genetic programming. A Soft Comput 22:949. https://doi.org/10.1007/s00500-016-2398-1

    Article  MATH  Google Scholar 

  • Ibrahim MK, Ali RS (2016) Novel optimization algorithm inspired by camel traveling behavior. Iraq J Electric Electron Eng 12:167–178

    Google Scholar 

  • Jeetendra A, Girish P Rajeev G, Afzal S (2018) Analysis of grey wolf optimizer based fractional order PID controller in speed control of DC motor. Microsystem Technologies pp 1–10

  • Karaboga D (2005) An idea based on honey bee swarm for numerical optimization, Technical Report-TR06, Erciyes University, Engineering Faculty, Computer Engineering Department

  • Karasakal O, Karasakale K (2004) A maximal covering location model in the presence of partial coverage. Comput Oper Res 31:1515–1526

    MathSciNet  MATH  Google Scholar 

  • Kumar Sharma T, Millie P (2018) Identification of noise in multi noise plant using enhanced version of shuffled frog leaping algorithm. Int J Syst Assur Eng Manage 9:43–51

    Google Scholar 

  • Lee JM, Lee YH (2010) Tabu based heuristics for the generalized hierarchical covering location problem. Comput Ind Eng 58:638–645

    Google Scholar 

  • Li Q, Zeng B, Savachkin A (2013) Reliable facility location design under disruptions. Comput Oper Res 40:901–909

    MathSciNet  MATH  Google Scholar 

  • Marianov V, Revelle C (1994) The queuing probabilistic location set covering problem and some extensions. Socioecon Plann Sci 28:167–178

    Google Scholar 

  • Marianov V, Serra D (2001) Hierarchical location–allocation models for congested systems. Eur J Oper Res 135:195–208

    MATH  Google Scholar 

  • Masegosa AD, de la Iglesia I, Hernandez-Jayo U, Diez LE, Bahillo A, Onieva E (2018) A New Approach for Information Dissemination in VANETs Based on Covering Location and Metaheuristics. In: Cruz Corona C (eds) Soft computing for sustainability science. studies in fuzziness and soft computing, vol 358. Springer, Cham

  • Moore GC, Revelle C (1982) The hierarchical service location problem. Manage Sci 28:775–780

    MATH  Google Scholar 

  • Murawski L, Church RL (2009) Improving accessibility to rural health services: The maximal covering network improvement problem. Socioecon Plann Sci 43:102–110

    Google Scholar 

  • O’hanleyChurch JRRL (2011) Designing robust coverage networks to hedge against worst-case facility losses. Eur J Oper Res 209:23–36

    MathSciNet  Google Scholar 

  • Peidro D, Mula J, Poler R, Verdegay JL (2009) Fuzzy optimization for supply chain planning under supply, demand and process uncertainties. Fuzzy Sets Syst 160:2640–2657

    MathSciNet  MATH  Google Scholar 

  • Qu B, Weng K (2009) Path relinking approach for multiple allocation hub maximal covering problem. Comput Math Appl 57:1890–1894

    MathSciNet  MATH  Google Scholar 

  • Rajagopalan HK, Saydam C, Xiao J (2008) A multiperiod set covering location model for dynamic redeployment of ambulances. Comput Oper Res 35:814–826

    MATH  Google Scholar 

  • Ratick SJ, Osleeb JP, Hozumi D (2009) Application and extension of the Moore and ReVelle hierarchical maximal covering model. Socioecon Plann Sci 43:92–101

    Google Scholar 

  • Repede JF, Bernado JJ (1994) Developing and validating a decision support system for locating emergency medical vehicles in Louisville, Kentucky. Eur J Oper Res 75:567–581

    Google Scholar 

  • Revelle CS, Eiselt HA (2005) Location analysis: a synthesis and survey. Eur J Oper Res 165:1–19

    MathSciNet  MATH  Google Scholar 

  • Revelle C, Scholssberg M, Williams J (2008a) Solving the maximal covering location problem with heuristic concentration. Comput Oper Res 35:427–435

    MathSciNet  MATH  Google Scholar 

  • Revelle CS, Eiselt HA, Daaskin MS (2008b) A bibliography for some fundamental problem categories in discrete location science. Eur J Oper Res 184:817–848

    MathSciNet  MATH  Google Scholar 

  • Şahin G, Sural H (2007) A review of hierarchical facility location models. Comput Oper Res 34:2310–2331

    MathSciNet  MATH  Google Scholar 

  • Sait A, Uymaz GT, E, (2013) Artificial algae algorithm(AAA) for nonlinear global optimization. Appl Soft Comput 31:153–157

    Google Scholar 

  • Schillingd A (1980) Dynamic location modeling for public-sector facilities: a multicriteria approach. Decis Sci 11:714–724

    Google Scholar 

  • Shandi H, Mahloohi H (2006) A fuzzy queuing location model with a genetic algorithm for congested systems. Appl Math Comput 181:440–456

    MathSciNet  Google Scholar 

  • Shandi H, Mahloohi H (2007) Fuzzy hierarchical location-allocation models for congested systems. J Indus Syst Eng 1:171–189

    Google Scholar 

  • Shen ZJM, Zhan RL, Zhang J (2011) The reliable facility location problem: formulations, heuristics, and approximation algorithms. INFORMS J Comput 23:470–482

    MathSciNet  MATH  Google Scholar 

  • Shi Y (2015) An optimization algorithm based on brainstorming process. Emerging Research on Swarm Intelligence and Algorithm Optimization, pp 1–35.

  • Snyder LV, Daskin MS (2005) Reliability models for facility location: the expected failure cost case. Transp Sci 39:400–416

    Google Scholar 

  • Xia L, Xie M, Xu W, Shao J, Yin W, Dong J (2009) An empirical comparison of five efficient heuristics for maximal covering location problems. Service Operations, Logistics and Informatics. SOLI'09 IEEE/INFORMS International Conference on IEEE 747–753

  • Younies H, Wesolowsky GO (2004) A mixed integer formulation for maximal covering by inclined parallelograms. Eur J Oper Res 159:83–94

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Industrial Engineering, Faculty of Engineering, Islamic Azad University, West Tehran Branch, Tehran, Iran

    Vahid Hajipour

  2. Department of Industrial Engineering, Faculty of Engineering, Alzahra University, Tehran, Iran

    Parviz Fattahi & Samaneh Babaei Morad

  3. Department of Industrial Engineering, Faculty of Engineering, Bu-Ali Sina University, Hamadan, Iran

    Hasan Bagheri

Authors
  1. Vahid Hajipour
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Parviz Fattahi
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Hasan Bagheri
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Samaneh Babaei Morad
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Vahid Hajipour.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hajipour, V., Fattahi, P., Bagheri, H. et al. Dynamic maximal covering location problem for fire stations under uncertainty: soft-computing approaches. Int J Syst Assur Eng Manag 13, 90–112 (2022). https://doi.org/10.1007/s13198-021-01109-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13198-021-01109-8

Keywords