Abstract
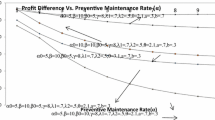
The main focus of this paper is on the reliability modelling of a computer system considering the concepts of redundancy, preventive maintenance and priority in repair activities. Two identical units of a computer system are taken—one unit is initially operative and the other is kept as spare in cold standby. In each unit h/w and s/w work together and may fail independently from normal mode. There is a single server who visits the system immediately as and when needed. Server conducts preventive maintenance of the unit (computer system) after a maximum operation time. Repair of the h/w is done at its failure while s/w is upgraded from time to time as per requirements. If server unable to repair the h/w in a pre-specific time (called maximum repair time), h/w is replaced by new one giving some replacement time. Priority to h/w repair is given over s/w up gradation if, in one unit s/w is under up-gradation and h/w fails in another operative unit. The failure time of h/w and s/w follows negative exponential distributions while the distributions of preventive maintenance, h/w repair/replacement and s/w up-gradation times are taken as arbitrary with different probability density functions. The expressions for several reliability and economic measures are derived in steady state using semi-Markov process and regenerative point technique. The graphical study of mean time to system failure (MTSF) and profit function has also been made giving particular values to various parameters and costs.



Similar content being viewed by others
Abbreviations
- E:
-
The set of regenerative states
- NO:
-
The unit is operative and in normal mode
- Cs:
-
The unit is cold standby
- a/b:
-
Probability that the system has hardware/software failure
- \( \lambda_{1} /\lambda_{2} \) :
-
Constant hardware/software failure rate
- α0 :
-
Maximum operation time
- β0 :
-
Maximum repair time
- Pm/PM:
-
The unit is under preventive maintenance/under preventive maintenance continuously from previous state
- WPm/WPM:
-
The unit is waiting for preventive maintenance/waiting for preventive maintenance from previous state
- HFur/HFUR:
-
The unit is failed due to hardware and is under repair/under repair continuously from previous state
- HFurp/HFURP:
-
The unit is failed due to hardware and is under replacement/under replacement continuously from previous state
- HFwr/HFWR:
-
The unit is failed due to hardware and is waiting for repair/waiting for repair continuously from previous state
- SFurp/SFURP:
-
The unit is failed due to the software and is under up-gradation/under up-gradation continuously from previous state
- SFwrp/SFWRP:
-
The unit is failed due to the software and is waiting for up-gradation/waiting for up-gradation continuously from previous state
- h(t)/H(t):
-
pdf/cdf of up-gradation time of unit due to software
- g(t)/G(t):
-
pdf/cdf of repair time of the hardware
- m(t)/M(t):
-
pdf/cdf of replacement time of the hardware
- f(t)/F(t):
-
pdf/cdf of the time for PM of the unit
- qij(t)/Qij(t):
-
pdf/cdf of passage time from regenerative state i to a regenerative state j or to a failed state j without visiting any other regenerative state in (0, t]
- pdf/cdf:
-
Probability density function/Cumulative density function
- qij.kr (t)/Qij.kr(t):
-
pdf/cdf of direct transition time from regenerative state i to a regenerative state j or to a failed state j visiting state k, r once in (0, t]
- μi(t):
-
Probability that the system up initially in state Si ∈ E is up at time t without visiting to any regenerative state
- Wi(t):
-
Probability that the server is busy in the state Si up to time ‘t’ without making any transition to any other regenerative state or returning to the same state via one or more non-regenerative states
- mij :
-
Contribution to mean sojourn time (μi) in state Si when system transit directly to state Sj so that \( \mu_{i} = \sum\limits_{j} {m_{ij} } \) and mij = \( \int {tdQ_{ij} (t) = - q_{ij}^{*} \prime (0)} \)
- \( \circledS \)/©:
-
Symbol for Laplace-Stieltjes convolution/Laplace convolution
- ~/*:
-
Symbol for Laplace Steiltjes Transform/Laplace Transform
- ‘(desh):
-
Used to represent alternative result
References
Friedman MA, Tran P (1992) Reliability techniques for combined hardware/software systems. In: Proceedings of annual reliability and maintability symposiym, pp 290–293
Kumar A, Malik SC, Barak MS (2012) Reliability modeling of a computer system with independent H/W and S/W failures subject to maximum operation and repair times. Int J Math Arch 3(7):2622–2630
Malik SC, Anand J (2010) Reliability and economic analysis of a computer system with independent hardware and software failures. Bull Pure Appl Sci 29E (Math. & Stat.)(1):141–153
Malik SC, Nandal P (2010) Cost-analysis of stochastic models with priority to repair over preventive maintenance subject to maximum operation time. Learning manual on modeling, optimization and their applications, Edited Book. Excel India Publishers, pp 165–178
Malik SC, Sureria JK (2012) Reliability and economic analysis of a computer system with priority to H/w repair over S/W replacement. Int J Stat Anal 2(4):379–389
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Malik, S.C. Reliability modeling of a computer system with preventive maintenance and priority subject to maximum operation and repair times. Int J Syst Assur Eng Manag 4, 94–100 (2013). https://doi.org/10.1007/s13198-013-0144-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13198-013-0144-y
Keywords
- Computer system
- Cold standby
- Preventive maintenance
- Maximum operation and repair times
- H/w repair and replacement
- S/w up-gradation
- Reliability measures
- Profit function