Attribute-oriented cognitive concept learning strategy: a multi-level method | International Journal of Machine Learning and Cybernetics Skip to main content
Springer Nature Link
Log in

Attribute-oriented cognitive concept learning strategy: a multi-level method

  • Original Article
  • Published:
International Journal of Machine Learning and Cybernetics Aims and scope Submit manuscript

Abstract

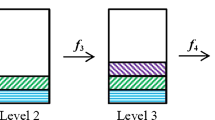
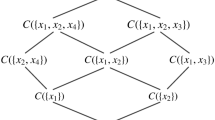
Recently, formal concept analysis has become a potential direction of cognitive computing, which can describe the processes of cognitive concept learning. We establish a concept hierarchy structure based on the existing cognitive concept learning methods. However, none of these methods could obtain the following results: get the concept, recognize objects and distinguish between two different objects. In this paper, our focus is to construct an attribute-oriented multi-level cognitive concept learning method so as to improve and enhance the ability of cognitive concept learning. Firstly, the view point of human cognition is discussed from the multi-level approach, and then the mechanism of attribute-oriented cognitive concept learning is investigated. Through some defined special attributes, we propose a corresponding structure of attribute-oriented multi-level cognitive concept learning from an interdisciplinary viewpoint. It is a combination of philosophy and psychology of human cognition. Moreover, to make the presented attribute-oriented multi-level method easier to understand and apply in practice, an algorithm of cognitive concept learning is established. Furthermore, a case study about how to recognize the real-world animals is studied to use the proposed method and theory. Finally, in order to solve conceptual cognition problems, we perform an experimental evaluation on five data sets downloaded from the University of California-Irvine (UCI) databases. And then we provide a comparative analysis with the existing \(granular\ computing\ approach\ to\ two\)-\(way\ learning\) [44] and the three-\(way\ cognitive\ concept\ learning\ via\ multi\)-granularity [9]. We obtain more number of concepts than \(the\ two\)-\(way\ learning\ and\ the\ three\)-\(way\ cognitive\ concept\ learning\ approaches\), which shows the feasibility and effectiveness of our attribute-oriented multi-level cognitive learning method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Agarwal GC (1991) Human cognition is an adaptive process. Behav Brain Sci 14(3):485–486

    Article  MathSciNet  Google Scholar 

  2. Bargiela A, Pedrycz W (2006) The roots of granular computing. In: IEEE international conference on granular computing, pp 806–809

  3. Belohlávek R, Baets BD, Outrata J, Vychodil V (2009) Inducing decision trees via concept lattices. In: International conference on concept lattices and their applications, Cla 2007, Montpellier, France, October, DBLP, pp 455–467

  4. Düntsch I, Gediga G (2002) Modal-style operators in qualitative data analysis. In: IEEE international conference on data mining, 2002, ICDM 2003, pp 155–162

  5. Ganter B (1999) Formal concept analysis: mathematical foundations. Springer, New York

    Book  MATH  Google Scholar 

  6. Huang C, Li J, Mei C, Wu WZ (2017) Three-way concept learning based on cognitive operators: an information fusion viewpoint. Int J Approx Reason 83:218–242

    Article  MathSciNet  MATH  Google Scholar 

  7. Konecny J (2017) On attribute reduction in concept lattices: methods based on discernibility matrix are outperformed by basic clarification and reduction. Inf Sci 415–416:199–212

    Article  Google Scholar 

  8. Kumar CA, Ishwarya MS, Loo CK (2015) Formal concept analysis approach to cognitive functionalities of bidirectional associative memory. Biol Inspir Cogn Archit 12:20–33

    Google Scholar 

  9. Li J, Huang C, Qi J, Qian Y, Liu W (2017) Three-way cognitive concept learning via multi-granularity. Inf Sci 378:244–263

    Article  Google Scholar 

  10. Li J, Mei C, Lv Y (2012) Knowledge reduction in real decision formal contexts. Inf Sci 189:191–207

    Article  MathSciNet  MATH  Google Scholar 

  11. Li J, Mei C, Lv Y (2013) Incomplete decision contexts: approximate concept construction, rule acquisition and knowledge reduction. Int J Approx Reason 54(1):149–165

    Article  MathSciNet  MATH  Google Scholar 

  12. Li J, Mei C, Xu W, Qian Y (2015) Concept learning via granular computing: a cognitive viewpoint. Inf Sci 298:447–467

    Article  MathSciNet  MATH  Google Scholar 

  13. Li J, Ren Y, Mei C, Qian Y, Yang X (2016) A comparative study of multigranulation rough sets and concept lattices via rule acquisition. Knowl Based Syst 91:152–164

    Article  Google Scholar 

  14. Li W, Pedrycz W, Xue X, Xu W, Fan B (2018) Distance-based double-quantitative rough fuzzy sets with logic operations. Int J Approx Reason 101:206–233

    Article  MathSciNet  MATH  Google Scholar 

  15. Liu M, Shao M, Zhang W, Wu C (2007) Reduction method for concept lattices based on rough set theory and its application. Comput Math Appl 53(9):1390–1410

    Article  MathSciNet  MATH  Google Scholar 

  16. Luksch P, Wille R (1991) A mathematical model for conceptual knowledge systems. Classification, data analysis, and knowledge organization. Springer, Berlin, pp 156–162

    Book  MATH  Google Scholar 

  17. Modha DS, Ananthanarayanan R, Esser SK, Ndirango A, Sherbondy AJ, Singh R (2011) Cognitive computing. Commun ACM 54(8):62–71

    Article  Google Scholar 

  18. Moreton E, Pater J, Pertsova K (2017) Phonological concept learning. Cogn Sci 41(1):4–69

    Article  Google Scholar 

  19. Pedrycz W, Skowron A, Kreinovich V (2008) Handbook of granular computing. Wiley-Interscience, Hoboken

    Book  Google Scholar 

  20. Pei D, Mi JS (2011) Attribute reduction in decision formal context based on homomorphism. Int J Mach Learn Cybern 2(4):289–293

    Article  Google Scholar 

  21. Pinggera J (2015) Visualizing human behavior and cognition: the case of process modeling. In: International conference on business process management, Springer, Cham, pp 547–551

  22. Qi J, Wei L, Yao Y (2014) Three-way formal concept analysis. In: International conference on rough sets and knowledge technology, Springer, Cham, pp 732–741

  23. Qi J, Qian T, Wei L (2016) The connections between three-way and classical concept lattices. Knowl Based Syst 91:143–151

    Article  Google Scholar 

  24. Rodríguez-Jiménez JM, Cordero P, Enciso M, Mora A (2014) A generalized framework to consider positive and negative attributes in formal concept analysis. In: Bertet K, Rudolph S (eds) Proceedings of the eleventh international conference on concept lattices and their applications, CLA 2014. Pavol Jozef Šafárik University in Košice, Slovakia, pp 267–279

    Google Scholar 

  25. Rodríguez-Jiménez JM, Cordero P, Enciso M, Rudolph S (2016) Concept lattices with negative information: a characterization theorem. Inf Sci 369:51–62

    Article  MathSciNet  Google Scholar 

  26. Shao M, Yang H (2013) Two kinds of multi-level formal concepts and its application for sets approximations. Int J Mach Learn Cybern 4(6):621–630

    Article  Google Scholar 

  27. Shivhare R, Cherukuri AK (2017) Three-way conceptual approach for cognitive memory functionalities. Int J Mach Learn Cybern 8(1):21–34

    Article  Google Scholar 

  28. Shivhare R, Cherukuri AK, Li J (2017) Establishment of cognitive relations based on cognitive informatics. Cogn Comput 9(5):721–729

    Article  Google Scholar 

  29. Singh PK, Cherukuri AK, Li J (2017) Concepts reduction in formal concept analysis with fuzzy setting using Shannon entropy. Int J Mach Learn Cybern 8(1):179–189

    Article  Google Scholar 

  30. Vormbrock B (2005) Complete subalgebras of semiconcept algebras and protoconcept algebras. In: International conference on formal concept analysis, Berlin, Heidelberg, pp 329–343

  31. Wang H, Zhang WX (2008) Approaches to knowledge reduction in generalized consistent decision formal context. Math Comput Model 48(11–12):1677–1684

    Article  MathSciNet  MATH  Google Scholar 

  32. Wang R, Wang XZ, Kwong S, Xu C (2017) Incorporating diversity and informativeness in multiple-instance active learning. IEEEE Trans Fuzzy Syst 25(6):1460–1475

    Article  Google Scholar 

  33. Wang XZ, Wang R, Xu C (2018) Discovering the relationship between generalization and uncertainty by incorporating complexity of classification. IEEE Trans Cybern 48(2):703–715

    Article  MathSciNet  Google Scholar 

  34. Wang XZ, He YL, Wang DD (2014) Non-naive Bayesian classifiers for classification problems with continuous attributes. IEEE Trans Cybern 44(1):21–39

    Article  Google Scholar 

  35. Wang XZ, Wang R, Feng HM, Wang HC (2014) A new approach to classifier fusion based on upper integral. IEEE Trans Cybern 44(5):620–635

    Article  MathSciNet  Google Scholar 

  36. Wang X, Xing HJ, Li Y, Hua Q, Dong CR, Pedrycz W (2015) A study on relationship between generalization abilities and fuzziness of base classifiers in ensemble learning. IEEE Trans Fuzzy Syst 23(5):1638–1654

    Article  Google Scholar 

  37. Wang Y (2008) On concept algebra: a denotational mathematical structure for knowledge and software modeling. Int J Cogn Inform Nat Intell 2(2):1–19

    Article  Google Scholar 

  38. Wang Y (2009) On cognitive computing. Int J Softw Sci Comput Intell 1(3):1–15

    Article  Google Scholar 

  39. Wang Y, Chiew V (2010) On the cognitive process of human problem solving. Cogn Syst Res 11(1):81–92

    Article  Google Scholar 

  40. Wang Y, Zadeh LA, Yao Y (2012) On the system algebra foundations for granular computing. In: Software and intelligent sciences: new transdisciplinary findings, \(|G|\) Global, pp 98–121

  41. Wille R (1992) Concept lattices and conceptual knowledge systems. Comput Math Appl 23(6–9):493–515

    Article  MATH  Google Scholar 

  42. Wille R (1982) Restructuring lattice theory: an approach based on hierarchies of concepts. Ordered sets. Springer, Dordrecht, pp 445–470

    MATH  Google Scholar 

  43. Wu WZ, Leung Y, Mi JS (2009) Granular computing and knowledge reduction in formal contexts. IEEE Trans Knowl Data Eng 21(10):1461–1474

    Article  Google Scholar 

  44. Xu W, Li W (2016) Granular computing approach to two-way learning based on formal concept analysis in fuzzy datasets. IEEE Trans Cybern 46(2):366–379

    Article  MathSciNet  Google Scholar 

  45. Xu W, Pang J, Luo S (2014) A novel cognitive system model and approach to transformation of information granules. Int J Approx Reason 55(3):853–866

    Article  MathSciNet  MATH  Google Scholar 

  46. Yao Y (2004) A comparative study of formal concept analysis and rough set theory in data analysis. In: International conference on rough sets and current trends in computing, Springer, Berlin, Heidelberg, pp 59–68

  47. Yao Y (2017) Interval sets and three-way concept analysis in incomplete contexts. Int J Mach Learn Cybern 8(1):3–20

    Article  Google Scholar 

  48. Yao Y (2009) Interpreting concept learning in cognitive informatics and granular computing. IEEE Trans Syst Man Cybern Part B (Cybern) 39(4):855–866

    Article  Google Scholar 

  49. Yao YY (2004) Concept lattices in rough set theory. Fuzzy Information, 2004, Processing NAFIPS’04. In: IEEE annual meeting of the IEEE, vol 2, pp 796–801

  50. Yao YY (2001) On modeling data mining with granular computing. In: Computer software and applications conference, COMPSAC, 2001 25th annual international. IEEE, pp 638–643

  51. Zhao Y, Li J, Liu W, Xu W (2017) Cognitive concept learning from incomplete information. Int J Mach Learn Cybern 8(1):159–170

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported by the Macau Science and Technology Development Fund (No. 081/2015/A3), the National Natural Science Foundation of China (No. 71471060, No. 61472463, and No. 61772002), the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJ1709221).

Author information

Authors and Affiliations

  1. Faculty of Information Technology, Macau University of Science and Technology, Taipa, Macau, People’s Republic of China

    Bingjiao Fan & Eric C. C. Tsang

  2. School of Mathematics and Statistics, Southwest University, Chongqing, 400715, People’s Republic of China

    Weihua Xu

  3. Department of Mathematics and Physics, North China Electric Power University, Beijing, 102206, People’s Republic of China

    Degang Chen

  4. Department of Mathematics, Harbin Institute of Technology, Harbin, 150001, People’s Republic of China

    Wentao Li

Authors
  1. Bingjiao Fan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Eric C. C. Tsang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Weihua Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Degang Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Wentao Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Eric C. C. Tsang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fan, B., Tsang, E.C.C., Xu, W. et al. Attribute-oriented cognitive concept learning strategy: a multi-level method. Int. J. Mach. Learn. & Cyber. 10, 2421–2437 (2019). https://doi.org/10.1007/s13042-018-0879-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s13042-018-0879-5

Keywords

Search

Navigation