Correlation coefficient of T-spherical type-2 hesitant fuzzy sets and their applications in clustering analysis | Journal of Ambient Intelligence and Humanized Computing Skip to main content

Advertisement

Springer Nature Link
Log in

Correlation coefficient of T-spherical type-2 hesitant fuzzy sets and their applications in clustering analysis

  • Original Research
  • Published:
Journal of Ambient Intelligence and Humanized Computing Aims and scope Submit manuscript

Abstract

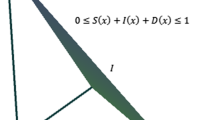
The fuzzy set (FS) theory has a significant role in the modelling of uncertainties. However, using the fuzzy set remain incapable in the modelling of the problems, when the decision-makers do not have the same opinion about the membership degree of an element or a decision-maker has different opinion related to membership degree of an element. To cope with this problem, the concept of a hesitant fuzzy set (HFS) was introduced by Torra and Narukawa. Recently, many generalizations of the FSs have been worked by researchers. One of them is type-2 fuzzy set (T2FS) and this set is an important role for dealing with problems involving uncertainty and linguistic variables. To take advantages of T2FSs and HFSs in the modelling of some problems into consideration, the concept of type-2 hesitant fuzzy sets (T2HFS) was defined. Another generalization of the FSs is spherical fuzzy set (SFS) and T-spherical fuzzy set (T-SFS) which is a generalization of SFS. In this research paper, to take advantages of T2HFSs and T-SFSs in the modelling of some problems into consideration, the concept of T-spherical type-2 hesitant fuzzy sets (T-ST2HFS) is defined and operations of union and intersection between two T-ST2HFSs. The basic idea behind of the set introduced in this paper is the assignment of T2HF elements for the components of a T-SFS. Then, a method is given to equalize lengths of the T2HF elements of which lengths are different from each other based on the optimistic and pessimistic approaches. The correlation coefficient is a very useful tool for dealing with some situations requiring the calculation of the relation between the two objects. With this motivation, correlation coefficients and weighted correlation coefficients are defined between proposed sets and some of their properties are obtained. Furthermore, a clustering analysis method, based on the put forward correlation coefficient formula is presented. Finally, to tackle a problem involving clustering the alternatives for a firm that wants to invest with a large amount of money, an application of the proposed method is given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  • Akram M (2020) Decision making method based on spherical fuzzy graphs. In: Otay I (ed) Kahraman C. Spherical fuzzy sets book. Studies in fuzziness and soft computing. Springer, Berlin

    Google Scholar 

  • Akram M, Saleem D, Al-Hawary T (2020a) Spherical fuzzy graphs with application to decision-making. Math Comput Appl 25(8):2–32. https://doi.org/10.3390/mca25010008

    Article  MathSciNet  Google Scholar 

  • Akram M, Alsulami S, Khan A, Karaaslan F (2020b) Multi-criteria group decision-making using spherical fuzzy prioritized weighted aggregation operators. Int J Comput Int Syst 13(1):1429–1446

    Google Scholar 

  • Ashraf S, Abdullah S, Mahmood T (2019a) Spherical fuzzy Dombi aggregation operators and their application in group decision making problems. J Amb Intel Hum Comput 11:2731–2749

    Google Scholar 

  • Ashraf S, Abdullah S, Mahmood T, Ghani F, Mahmood T (2019b) Spherical fuzzy sets and their applications in multi-attribute decision making problems. J Intell Fuzzy Syst 36(3):2829–2844

    Google Scholar 

  • Ashraf S, Abdullah S, Aslam M, Qias M, Kutbi MA (2019c) Spherical fuzzy sets and its representation of spherical fuzzy t-norms and t-conorms. J Intell Fuzzy Syst 36(6):6089–6102

    Google Scholar 

  • Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96

    MATH  Google Scholar 

  • Bustince H, Burillo P (1995) Correlation of interval valued intuitionistic fuzzy sets. Fuzzy Set Syst 74:237–244

    MathSciNet  MATH  Google Scholar 

  • Chaneau JL, Gunaratne M, Altschaev AG (1987) An application o type-2 sets to decision making in engineering. In: Bezdek JC (ed) Analysis of fuzzy in formation-vol II: artificial intelligence and decision systems. CRC Press Inc, Boca Raton

    Google Scholar 

  • Chen N, Xu Z, Xia M (2013a) Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis. Appl Math Modell 37(4):2197–2211

    MathSciNet  MATH  Google Scholar 

  • Chen N, Xu ZS, Xia MM (2013b) Interval-valued hesitant preference relations and their applications to group decision making. Knowl-Based Syst 37:528–540

    Google Scholar 

  • Chen ZS, Yang Y, Wang XJ, Chin KS, Tsui KL (2019) Fostering linguistic decision-making under uncertainty: a proportional interval type-2 hesitant fuzzy TOPSIS approach based on Hamacher aggregation operators and andness optimization models. Inf Sci 500:229–258

    Google Scholar 

  • Cuong B (2013) Picture fuzzy sets-first results. part 1. In: Seminar “Neuro-Fuzzy Systems with Applications”. Institute of Mathematics, Hanoi

  • Dubois D, Prade H (1980) Fuzzy sets and systems: theory and applications. Academic Press Inc, New York

    MATH  Google Scholar 

  • Dumitrescu D (1977) A definition of an informational energy in fuzzy sets theory. Stud Univ Babes Bolvai Ser Math 2:57–59

    MathSciNet  MATH  Google Scholar 

  • Farhadinia B (2013) Information measures for hesitant fuzzy sets and interval-valued hesitant fuzzy sets. Inf Sci 240:129–144

    MathSciNet  MATH  Google Scholar 

  • Garg H, Munir M, Ullah K, Mahmood T, Jan N (2018) Algorithm for T-spherical fuzzy multi-attribute decision making based on improved interactive aggregation operators. Symmetry 10(12):670

    Google Scholar 

  • Gerstenkorn T, Manko J (1991) Correlation of intuitionistic fuzzy sets. Fuzzy Sets Syst 44:39–43

    MathSciNet  MATH  Google Scholar 

  • Guleria A, Bajaj RK (2020) T-spherical fuzzy graphs: operations and applications in various selection process. Arab J Sci Eng 45:2177–2193

    Google Scholar 

  • Gundogdu FK, Kahraman C (2019a) Spherical fuzzy sets and spherical fuzzy TOPSIS method. J Intell Fuzzy Syst 36(1):337–352

    Google Scholar 

  • Gundogdu FK, Kahraman C (2019b) Spherical fuzzy sets and decision making applications. In: Kahraman C, Cebi S, Cevik Onar S, Oztaysi B, Tolga A, Sari I (eds) Intelligent and fuzzy techniques in big data analytics and decision making. INFUS 2019. Advances in intelligent systems and computing, vol 1029. Springer, Cham (2020)

  • Gundogdu, FK, Kahraman C, Onar SC, Oztaysi B (2019) Hospital location selection using spherical fuzzy TOPSIS. In: 2019 conference of the international fuzzy systems association and the European Society for Fuzzy Logic and Technology (EUSFLAT 2019). Atlantis Press

  • Feng L, Chuan-qiang F, Wei-he X (2018) Type-2 hesitant fuzzy sets. Fuzzy Inf Eng 10(2):249–259

    Google Scholar 

  • Hagras H (2004) A hierarchical type-2 fuzzy logic control architecture for autonomous mobile robots. IEEE Trans Fuzzy Syst 4(12):524–539

    Google Scholar 

  • Huang J, You XY, Liu HC, Si SL (2019) New approach for quality function deployment based on proportional hesitant fuzzy linguistic term sets and prospect theory. Int J Prod Res 57(5):1283–1299

    Google Scholar 

  • Hung WL, Yang MS (2004) Similarity measures between type-2 fuzzy sets. Int J Uncertain Fuzzy 12(6):827–841

    MathSciNet  MATH  Google Scholar 

  • Hwang CM, Yang MS, Hung WL, Stanley LE (2011) Similarity, inclusion and entropy measures between type-2 fuzzy sets based on the sugeno integral. Math Comput Model 53(9):1788–1797

    MathSciNet  MATH  Google Scholar 

  • Innocent P, John R (2002) Type 2 fuzzy diagnosis. IEEE Int Conf Fuzzy Syst 2:1326–1330

    Google Scholar 

  • Innocent P, John R, Belton I, Finlay D (2001) Type 2 fuzzy representations of lung scans to predict pulmonary emboli. In: Proceedings of 2001 IFSA/NAFIPS joint conference, Vancouver, BC, Canada, Jul 2001, pp 1902–1907

  • John R (1996) Type-2 inferencing and community transport scheduling. In: Proceedings of 4th European Congress Intelligent Techniques Soft Computing, Aachen, Germany, 1996, pp 1369–1372

  • John R (1998) Type 2 fuzzy sets, an appraisal of theory and applications. Int J Uncertain Fuzzy 6(6):563–576

    MathSciNet  MATH  Google Scholar 

  • John RI, Innocent PR, Barnes MR (1997) Type-2 fuzzy sets and neuro-fuzzy clustering or radiographic tibia images. In: Proceedings of 6th international conference on fuzzy systems, Barcelona, Spain, 1997, pp 1375–1380

  • Karaaslan F, Ozlu S (2020) Correlation coefficients of dual type2 hesitant fuzzy sets and their applications in clustering analysis. Int J Intell Syst 35:1200–1229

    Google Scholar 

  • Karnik N, Mendel J (1999) Applications of type-2 fuzzy logic systems to forecasting of time series. Inf Sci 120:89–111

    MATH  Google Scholar 

  • Liang Q, Mendel J (2001) MPEG VBR video traffic modeling and classification using fuzzy techniques. IEEE Trans Fuzzy Syst 1(9):183–193

    Google Scholar 

  • Liao H, Xu Z (2013) A VIKOR-based method for hesitant fuzzy multi-criteria decision making. Springer, New York

    MATH  Google Scholar 

  • Liao HC, Yang LY, Xu ZS (2018) Two new approaches based on ELECTRE II to solve the multiple criteria decision making problems with hesitant fuzzy linguistic term sets. Appl Soft Comput 63:223–234

    Google Scholar 

  • Liu P, Khan Q, Mahmood T, Hassan N (2019) T-spherical fuzzy power muirhead mean operator based on novel operational laws and their application in multi-attribute group decision making. IEEE 7:22613–22632

    Google Scholar 

  • Mahmood T, Ullah K, Khan Q, Jan N (2018) An approach towards decision making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput Appl 31:7041–7053

    Google Scholar 

  • Mitchell HB (2006) Correlation coefficient for type-2 fuzzy sets. Wiley Period 21(2):143–153

    MATH  Google Scholar 

  • Mizumoto M, Tanaka K (1976) Some properties of fuzzy sets of type-2. Inf Control 31:312–340

    MathSciNet  MATH  Google Scholar 

  • Mizumoto M, Tanaka K (1981) Fuzzy sets of type 2 under algebraic product and algebraic sum. Fuzzy Sets Syst 5:277–290

    MathSciNet  MATH  Google Scholar 

  • Mendel JM, John RB (2002) Type-2 fuzzy sets made simple. IEEE Trans Fuzzy Syst 10(2):117–127

    Google Scholar 

  • Mendel J, Hani H, Sola HB, Herrera F (2014) Interval type-2 fuzzy sets are generalization of interval-valued fuzzy sets: toward a wider view on their relationship. IEEE Trans Fuzzy Syst 23(5):1876–1882

    Google Scholar 

  • Munir M, Kalsoom H, Ullah K, Mahmood T, Chu YM (2020) T-Spherical Fuzzy Einstein Hybrid Aggregation Operators and Their Applications in Multi-Attribute decision making problems. Symmetry 12:365

    Google Scholar 

  • Nieminen J (1977) On the algebraic structure of fuzzy sets of type-2. Kybernetica 13(4):261–273

    MathSciNet  MATH  Google Scholar 

  • Ozlu S, Karaaslan F (2020) Some distance measures for Type-2 hesitant fuzzy sets and their application to multi-criteria group decision making problems. Soft Comput 24:9965–9980

    Google Scholar 

  • Peng DH, Gao CY, Gao ZF (2013) Generalized hesitant fuzzy synergetic weighted distance measures and their application to multiple criteria decisionmaking. Appl Math Modell 37:5837–5850

    MATH  Google Scholar 

  • Peng JJ, Wang JQ, Wang J, Yang LJ, Chen XH (2015) An extension of ELECTRE to multi-criteria decision-making problems with multi-hesitant fuzzy sets. Inf Sci 307:113–126

    MathSciNet  MATH  Google Scholar 

  • Qian G, Wang H, Feng X (2013) Generalized hesitant fuzzy sets and their application in decision support system. Knowl Based Syst 37:357–365

    Google Scholar 

  • Quek SG, Selvachandran G, Munir M, Mahmood T, Ullah K, Son LH, Thong PH, Kumar R, Priyadarshini I (2019) Multi-attribute multi-perception decision-making based on generalized T-spherical fuzzy weighted aggregation operators on neutrosophic sets. Mathematics 7:780

    Google Scholar 

  • Rodriguez RM, Martinez L, Herrera F (2014a) Hesitant fuzzy linguistic term sets for decision making. IEEE Trans Fuzzy Syst 20:109–119

    Google Scholar 

  • Rodriguez RM, Martinez L, Torra V, Xu ZS, Herrera F (2014b) Hesitant fuzzy sets: state of the art and future directions. Int J Intell Syst 29:495–524

    Google Scholar 

  • Sahin R, Liu P (2017) Correlation coefficients of single valued neutrosophic hesitant fuzzy sets and their applications in decision making. Neural Comput Appl 28:1387–1395

    Google Scholar 

  • Sellak H, Ouhbi B, Frikh B (2018) A knowledge-based outranking approach for multi-criteria decision-making with hesitant fuzzy linguistic term sets. Appl Soft Comput 67:625–640

    Google Scholar 

  • Singh P (2014) Some new distance measures for type-2 fuzzy sets and distance measure based ranking for group decision making problems. Front Comput Sci 8(5):741–752

    MathSciNet  MATH  Google Scholar 

  • Torra V (2010) Hesitant fuzzy sets. Int J Intell Syst 25:529–539

    MATH  Google Scholar 

  • Torra V, Narukawa Y (2009) On hesitant fuzzy sets and decision. In:18th IEEE international conference on fuzzy systems. Jeju Island, Korea 2009:1378–1382

    Google Scholar 

  • Ullah K, Mahmood T, Jan N (2014) Similarity measures for T-spherical fuzzy sets with applications in pattern recognition. Symmetry 10(6):193

    MATH  Google Scholar 

  • Ullah K, Mahmood T, Jan N, Ali Z (2018) A note on geometric aggregation operators in T-spherical fuzzy environment and their applications in multi-attribute decision making. J Eng Appl Sci 37(2):75–86

    Google Scholar 

  • Ullah K, Hassan N, Mahmood T, Jan N, Hassan M (2019) Evaluation of investment policy based on multi-attribute decision-making using interval valued T-spherical fuzzy aggregation operators. Symmetry 11(3):357

    Google Scholar 

  • Ullah K, Mahmood T, Garg H (2020a) Evaluation of the performance of search and rescue robots using T-spherical fuzzy Hamacher aggregation operators. Int J Fuzzy Syst 22:570–582

    Google Scholar 

  • Ullah K, Garg H, Mahmood T, Jan N, Ali Z (2020b) Correlation coefficients for T-spherical fuzzy sets and their applications in clustering and multi-attribute decision making. Soft Comput 24:1647–1659

    MATH  Google Scholar 

  • Wang PZ (1983) Fuzzy set theory and applications. Shanghai Scientific and Technical Publishers, Shanghai

    Google Scholar 

  • Wei CP, Ren ZL, Rodriguez RM (2014) A hesitant fuzzy linguistic TODIM method based on a score function. Int J Comput Intell Syst 8(4):701–712

    Google Scholar 

  • Wu K (1996) Fuzzy interval control of mobile robots. Comput Electr Eng 22:211–229

    Google Scholar 

  • Wu M, Chen T, Fan J (2020) Divergence measure of T-spherical fuzzy sets and its applications in pattern recognition. IEEE 8:10208–10221

    Google Scholar 

  • Xu Z, Xia MM (2012) Hesitant fuzzy entropy and cross-entropy and their use in multiattribute decision making. Int J Intell Syst 27:799–822

    Google Scholar 

  • Xu Z, Chen J, Wu J (2008) Clustering algorithm for intuitionistic fuzzy sets. Inf Sci 178(19):3775–3790

    MathSciNet  MATH  Google Scholar 

  • Yager RR (1980) Fuzzy subsets o type II in decisions. J Cybernet 10:137–159

    MathSciNet  Google Scholar 

  • Yager RR (2013a) Pythagorean fuzzy subsets. 2013 Joint IFSA world congress and NAFIPS annual meeting (IFSA-NAFIPS) (2013), pp 57-61

  • Yager RR (2013b) Pythagorean membership grades in multi-criteria decision making. IEEE Trans Fuzzy Syst 22(4):958–965

    Google Scholar 

  • Yang MS, Lin DC (2009) On similarity and inclusion measures between type-2 fuzzy sets with an application to clustering. Comput Math Appl 57(6):896–907

    MathSciNet  MATH  Google Scholar 

  • Yang MS, Shih HM (2001) Cluster analysis based on fuzzy relations. Fuzzy Sets Syst 120(2):197–212

    MathSciNet  MATH  Google Scholar 

  • Yang Y, Chin KS, Ding H, Lv HX, Li YL (2019) Pythagorean fuzzy Bonferroni means based on T-norm and its dual T-conorm. Int J Int Syst 34(6):1303–1336

    Google Scholar 

  • Ye J (2015) Multiple-attribute decision-making method under a single-valued neutrosophic hesitant fuzzy environment. J Intell Syst 24:23–36

    Google Scholar 

  • Zadeh LA (1965) Fuzzy sets. Inform Comput 8:338–353

    Google Scholar 

  • Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning-1. Inf Sci 8:199–249

    MathSciNet  MATH  Google Scholar 

  • Zeng S, Garg H, Munir M, Mahmood T, Hussain AA (2019) Multi-attribute decision making process with immediate probabilistic interactive averaging aggregation operators of T-spherical fuzzy sets and its application in the selection of solar cells. Energies 12(23):4436

    Google Scholar 

  • Zhao H, Xu Z, Wang Z (2013) Intuitionistic fuzzy clustering algorithm based on Boolean matrix and association measure. Int J Inf Technol Decis Mak 12(1):95–118

    Google Scholar 

  • Zhang XL, Xu ZS (2014) The TODIM analysis approach based on novel measured functions under hesitant fuzzy environment. Knowl Based Syst 61:48–58

    Google Scholar 

  • Zhong X, Xu X (2020) Clustering-based method for large group decision making with hesitant fuzzy linguistic information: Integrating correlation and consensus. Appl Soft Comput 87:105973

    Google Scholar 

  • Zhu B, Xu Z, Xia M (2012) Dual hesitant fuzzy sets. J Appl Math Article ID 879629:13

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Nizip Vocational High School, Gaziantep University, Gaziantep, Turkey

    Şerif Özlü

  2. Department of Mathematics, Faculty of Science, Çankırı Karatekin University, 18100, Çankırı, Turkey

    Faruk Karaaslan

Authors
  1. Şerif Özlü
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Faruk Karaaslan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Faruk Karaaslan.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Özlü, Ş., Karaaslan, F. Correlation coefficient of T-spherical type-2 hesitant fuzzy sets and their applications in clustering analysis. J Ambient Intell Human Comput 13, 329–357 (2022). https://doi.org/10.1007/s12652-021-02904-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12652-021-02904-8

Keywords

Search

Navigation