Echo state network based on improved fruit fly optimization algorithm for chaotic time series prediction | Journal of Ambient Intelligence and Humanized Computing Skip to main content
Springer Nature Link
Log in

Echo state network based on improved fruit fly optimization algorithm for chaotic time series prediction

  • Original Research
  • Published:
Journal of Ambient Intelligence and Humanized Computing Aims and scope Submit manuscript

Abstract

Chaos is a common phenomenon in nature and society. Chaotic system affects many fields. It is of great significance to find out the regularity of chaotic time series from chaotic system. Chaotic system has extremely complex dynamic characteristics and unpredictability. The traditional prediction methods for chaotic time series have some problems, such as low accuracy, slow convergence speed and complex model structure. In this paper, an echo state network prediction method based on improved fruit fly optimization algorithm for chaotic time series is proposed. The phase space reconstruction is introduced for the prediction of chaotic time series. The C–C method is used to determine the delay time. The embedding dimension is obtained by the G–P method. After reconstructing the phase space of the chaotic time series, an improved echo state network is proposed as the prediction model. In order to improve the prediction accuracy, an improved fruit fly optimization algorithm is proposed to optimize the parameters of the prediction model. Three typical chaotic time series, including Lorenz, Mackey–Glass, and short-term wind speed, are selected as simulation objects. The simulation results show that the prediction method proposed in this paper has good prediction indicators. At the same time, the results of the reliability and Pearson's test also show the better predictive effect.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25
Fig. 26
Fig. 27
Fig. 28
Fig. 29
Fig. 30

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Abbreviations

ARMA:

Auto regressive moving average

ARIMA:

Auto regressive integrated moving average

ELM:

Extreme learning machine

SVM:

Support vector machine

LSSVM:

Least squares support vector machine

ESN:

Echo state network

FOA:

Fruit fly optimization algorithm

C–C:

Correlation–correlation

GP:

Grassberger–Procaccia

DR:

Dynamic reservoir

SR:

Spectral radius

SD:

Sparse degree

IS:

Input scale

RMSE:

Root mean square error

MAE:

Mean absolute error

MAPE:

Mean absolute percentile error

\({R^{2}}\) :

R square

EMD:

Empirical mode decomposition

\(\tau\) :

Delay time

m :

Embedding dimension

\(x(k)\) :

Time series at sampling time k

\(\overline{x} (k)\) :

Predictive value of time series at sampling time k

\(\overline{x}\) :

The mean value of chaotic time series

\(N\) :

The length of time series

M :

The amount of m-dimensional phase points

\(\mathop S\limits^{\_} (t)\) :

Average test statistics

\(\Delta \mathop S\limits^{\_} (t)\) :

Mean deviation

\(\varepsilon\) :

The standard deviation of time series

r :

The multiple of deviation

\(n_{m}\) :

The number of possible values of m

\(n_{k}\) :

The number of possible values of r

\(D_{m}\) :

Searching radius

\(C_{n} (r)\) :

Correlation integral

\(\theta ()\) :

Heaviside unit function

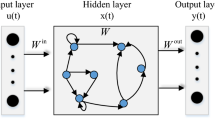
\({\mathbf{W}}_{in}\) :

Input weight matrix

\({\mathbf{W}}_{out}\) :

Output weight matrix

\({\mathbf{u}}(k)\) :

Input of ESN

K :

Input layers of ESN

B :

Internal processing units of ESN

L :

Output layers of ESN

U :

Input matrix of ESN

Y :

Output matrix of ESN

\(c\) :

Compensation signal

K :

Input layers of ESN

\(\alpha\) :

Ratio coefficient of reservoir

β :

Output feedback coefficient of reservoir

\(\lambda _{{\max }}\) :

The absolute value of the largest eigenvalue of connection weight matrix of ESN

\(X_{i}^{best}\) :

Abscissa of the position coordinates of the optimal individual

\(Y_{i}^{best}\) :

Ordinate of the position coordinates of the optimal individual

\(X_{i}^{{{\text{Secbest}}}}\) :

Abscissa of the position coordinates of the sub-optimal individual

\(Y_{i}^{{{\text{Secbest}}}}\) :

Ordinate of the position coordinates of the sub-optimal individual

\(X\_{\text{axis}}\) :

Abscissa of the coordinates of the position after the movement of the ith fruit fly

\(Y\_{\text{axis}}\) :

Ordinate of the position coordinates of the sub-optimal individual

DIST:

The optimal individual is the minimum distance

\(S_{i}\) :

The determination of the smell concentration of each fruit fly individual in populations

\({\text{Dist}}_{{{\text{best}}}}\) :

The distance of the fruit fly individual and the origin

t :

The iterative algebra

\(\eta\) :

The threshold

NI :

The amount of all individuals

\({\rm smell}_{{best}}^{r}\) :

The determination of the smell concentration of the optimal individual at the tth iteration

\({\rm smell}_{{best}}^{t}\) :

The sum of the determination of the smell concentration of all individuals at the tth Iteration

pos_up:

The lower limit of the fruit fly's search range

pos_low:

The upper limit of the fruit fly's search range

NI :

The amount of all individuals

maxgen:

Maximum amount of iterations

sizepop:

The size of the fruit fly population

\(\xi ^{{(1 - a)}}\) :

The amount of actual values falling into the confidence interval under the confidence level 1−α

\(\Delta T\) :

Sampling interval of Lorenz time series

\(\Delta\) :

Delay parameter of Mackey-Glass time series

γ :

Regularization parameters of LSSVM

\(\delta^{2}\) :

Radial basis function width of LSSVM

λ :

Sigmoid function parameter

μ :

Scale factor of the improved ELM

a, b:

Parameters to be estimated of grey model

\(c_{1} ,c_{2}\) :

Weight coefficient of hybrid prediction model

ρ :

Discard probability

References

  • Adewumi A, Kagamba A, Alochukwu A (2016) Application of chaos theory in the prediction of motorised traffic flows on urban networks. Math Prob Eng 5656734:15

    Google Scholar 

  • Bala A, Ismail I, Ibrahim R, Sait SM (2018) Applications of metaheuristics in reservoir computing techniques: a review. IEEE Access 6:58012–58029

    Google Scholar 

  • Camastra F, Vinciarelli A (2002) Estimating the intrinsic dimension of data with a fractal-based method. IEEE Trans Pattern Anal Mach Intell 24(10):1404–1407

    Google Scholar 

  • Chai SH (2015) Forecasting business cycle with chaotic time series based on neural network with weighted fuzzy membership functions. Chaos Solitons Fractals 90:118–126

    MathSciNet  MATH  Google Scholar 

  • Chandra R (2015) Competition and collaboration in cooperative coevolution of Elman recurrent neural networks for time-series prediction. IEEE Trans Neural Netw Learn Syst 26(12):3123–3136

    MathSciNet  Google Scholar 

  • Chen X, Li FW, Feng P (2018) A new hybrid model for nonlinear and non-stationary runoff prediction at annual and monthly time scales. J Hydro Environ Res 20:77–92

    Google Scholar 

  • Chikh R, Chikhi S (2019) Clustered negative selection algorithm and fruit fly optimization for email spam detection. J Ambient Intell Hum Comput 10(1):143–152

    Google Scholar 

  • Chouikhi N, Ammar B, Rokbani N, Alimi AM (2017) PSO-based analysis of Echo State Network parameters for time series forecasting. Appl Soft Comput 55:211–225

    Google Scholar 

  • Deng HL, Li B, Xiang YY, Dun GT (2016) Comparison of chaotic and fractal properties of polar faculae with sunspot activity. Astron J 151(1):2

    Google Scholar 

  • Du TS, Ke XT, Liao JG, Shen YJ (2018) DSLC-FOA: improved fruit fly optimization algorithm for application to structural engineering design optimization problems. Appl Math Model 55:314–339

    MathSciNet  MATH  Google Scholar 

  • Fang LD, Zeng QQ, Faraj Y, Zhao N, Wei ZH, Li XT (2019) Analysis of chaos characteristics of gas-liquid two-phase flow noise. Flow Meas Instrum 65:98–109

    Google Scholar 

  • Garg N, Soni K, Saxen TK, Maji S (2015) Applications of AutoRegressive integrated moving average (ARIMA) approach in time-series prediction of traffic noise pollution. Noise Control Eng J 63(2):182–194

    Google Scholar 

  • Guo W, Xu T, Lu LZ (2016) An integrated chaotic time series prediction model based on efficient extreme learning machine and differential evolution. Neural Comput Appl 27(4):883–898

    Google Scholar 

  • Guo YN, Liu QJ, Wang YH, Sun CL, Tian WY, Naik GR, Abraham A (2017a) Optimized phase-space reconstruction for accurate musical-instrument signal classification. Multimed Tools Appl 76(20):20719–20737

    Google Scholar 

  • Guo YN, Liu QJ, Wang AH (2017b) Optimized phase-space reconstruction for accurate musical-instrument signal classification. Multimed Tools Appl 76(20):20719–20737

    Google Scholar 

  • Henrique BM, Sobreiro VA, Kimura H (2019) Literature review: Machine learning techniques applied to financial market prediction. Expert Syst Appl 124:226–251

    Google Scholar 

  • Huang FM, Huang JS, Jiang SH, Zhou CB (2017) Landslide displacement prediction based on multivariate chaotic model and extreme learning machine. Eng Geol 218:173–186

    Google Scholar 

  • Jaeger H, Haas H (2004) Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 304:78–80

    Google Scholar 

  • Jiang P, Wang B, Li HM, Lu HY (2019) Modeling for chaotic time series based on linear and nonlinear framework: application to wind speed forecasting. Energy 173:468–482

    Google Scholar 

  • Kim HS, Eykholt R, Salas JD (1999) Nonlinear dynamics, delay times, and embedding windows. Physica D 127:48–60

    MATH  Google Scholar 

  • Li K, Han Y (2018) Modelling for motor load torque with dynamic load changes of beam pumping units based on a serial hybrid model. Trans Inst Meas Control 40(3):603–917

    MathSciNet  Google Scholar 

  • Li K, Xu WS, Han Y, Ge FW, Wang YA (2019) Soft sensor for the moisture content of crude oil based on multi-kernel Gaussian process regression optimized by an adaptive variable population fruit fly optimization algorithm. Trans Inst Meas Control. https://doi.org/10.1177/0142331219878959

    Article  Google Scholar 

  • Li YL, Zhang YP, Wang J, Huang B, Liu WX (2016) The Volterra adaptive prediction method based on matrix decomposition. J Interdiscip Math 19(2):363–377

    Google Scholar 

  • Lin GY (2012) Prediction of chaotic time series using least square support vector machines. Adv Inform Sci Serv Sci 4(5):21–27

    Google Scholar 

  • Liu JZ (2017) Adaptive forgetting factor OS-ELM and bootstrap for time series prediction. Int J Model Simul Sci Comput 8(3):1750029

    Google Scholar 

  • Liu LJ, Fu Y, Ma SW (2014) Wind power Short-Term prediction method based on multivariable mutual information and phase space reconstruction. Int Conf Intell Comput Sustain Energy Environ 463:1–12

    Google Scholar 

  • Lukoseviciute K, Baubliene R, Howard D, Ragulskis M (2018) Bernstein polynomials for adaptive evolutionary prediction of short-term time series. Appl Soft Comput 65:45–57

    Google Scholar 

  • Ma JH, Chen YS, Xin BG (2004) Study on prediction methods for dynamic systems of nonlinear chaotic time series. Appl Math Mech (Eng Ed) 25(6):605–611

    MATH  Google Scholar 

  • Milad HSA, Farooq U, EI-Hawary ME, Usman M (2017) Neo-Fuzzy integrated adaptive decayed brain emotional learning network for online time series prediction. IEEE Access 5:1037–1049

    Google Scholar 

  • Miranian A, Abdollahzade M (2013) Developing a local least-squares support vector machines-based neuro-fuzzy model for nonlinear and chaotic time series prediction. IEEE Trans Neural Netw Learn Syst 24(2):207–218

    Google Scholar 

  • Niu W, Wang GQ, Zhai ZJ, Cheng J (2011) Prediction of chaotic time series based on rough sets and support vector machine. Int J Digit Content Tech Appl 5(9):145–152

    Google Scholar 

  • Pan WT (2012) A new fruit fly optimization algorithm: taking the financial distress model as an example. Knowl Based Syst 26(2):69–74

    Google Scholar 

  • Peng YP (2016) Chaotic time series prediction based on rbf neural network. Revista Tecnica de la Facultad de Ingenieria Universidad del Zulia 39(1):339–345

    Google Scholar 

  • Qiao JF, Li FJ, Han HG, Li WJ (2017) Growing echo-state network with multiple subreservoirs. IEEE Trans Neural Netw Learn Syst 28(2):391–404

    Google Scholar 

  • Qiao JF, Wang L, Yang CL, Gu K (2018) Adaptive Levenberg–Marquardt algorithm based echo state network for chaotic time series prediction. IEEE Access 6:10720–70732

    Google Scholar 

  • Rojas I, Valenzuela O, Rojas A, Guillen A, Herreta LJ, Pomares H, Marquez L, Pasadas M (2008) Neurocomputing 71(4–6):519–537

    Google Scholar 

  • Shabestari PS, Panahi B, Hatef B, Jafari S, Sprott JC (2018) A new chaotic model for glucose-insulin regulatory system". Chaos Solitons Fractals 112:44–51

    MathSciNet  Google Scholar 

  • Song Y, Li YB, Wang Q, Li CH (2010) Multi-steps prediction of chaotic time series based on echo state network. Proceedings In: 2010 IEEE 5th International Conference on Bio-Inspired Computing: Theories and Applications, pp 669–672.

  • Sun XC, Li T, Li Q (2017) Deep belief echo-state network and its application to time series prediction. Knowl Based Syst 130:17–29

    Google Scholar 

  • Tian ZD, Li SJ (2017) A network traffic prediction method based on IFS algorithm optimised LSSVM. Int J Eng Syst Model Simul 9(4):200–213

    Google Scholar 

  • Tian ZD, Li SJ, Wang YH, Sha Y (2017) A prediction method based on wavelet transform and multiple models fusion for chaotic time series. Chaos Solitons Fractals 98:158–172

    MathSciNet  MATH  Google Scholar 

  • Tian ZD, Li SJ, Wang YH, Wang XD (2015) A network traffic hybrid prediction model optimized by improved harmony search algorithm. Neural Netw World 25(6):669–686

    Google Scholar 

  • Tian ZD, Ren Y, Wang G (2018) Short-term wind power prediction based on empirical mode decomposition and improved extreme learning machine. J Elect Eng Tech 13(5):1841–1851

    Google Scholar 

  • Wang RX, Gao JM, Gao ZY, Gao X, Jiang HQ, Gui L (2015) Data fusion based phase space reconstruction from multi-time series. Int J Datab Theory Appl 8(6):101–110

    Google Scholar 

  • Wang YL, Hu FX, Cao Y, Yuan XF, Yang CH (2019) Improved CCM for variable causality detection in complex systems. Control Eng Pract 83:67–82

    Google Scholar 

  • Wang C, Zhang HL, Fan WH, Ma P (2017a) A new chaotic time series hybrid prediction method of wind power based on EEMD-SE and full-parameters continued fraction. Energy 138:977–990

    Google Scholar 

  • Wang HS, Ni CJ, Yan XF (2017b) Optimizing the echo state network based on mutual information for modeling fed-batch bioprocesses. Neurocomputing 225:111–118

    Google Scholar 

  • Wang JZ, Yang WD, Du P, Niu T (2018) A novel hybrid forecasting system of wind speed based on a newly developed multi-objective sine cosine algorithm. Energy Convers Manage 163:134–150

    Google Scholar 

  • Xu ML, Han M (2016) Adaptive elastic echo state network for multivariate time series prediction. IEEE Trans Cybern 46(10):2173–2183

    Google Scholar 

  • Yang L, Zhang JX, Wu XJ, Zhang YM, Li JJ (2016) A chaotic time series prediction model for speech signal encoding based on genetic programming. Appl Soft Comput J 38:754–761

    Google Scholar 

  • Yuan YP, An ZL, Sun YT (2018) Prediction model of nonlinear combination based on support vector machine. Int J Circ Syst Signal Process 12:399–404

    Google Scholar 

Download references

Acknowledgements

This paper is supported by the Science Research Project of Liaoning Education Department (No. LGD2016009), Natural Science Foundation of Liaoning Province of China (No. 20170540686).

Author information

Authors and Affiliations

  1. College of Information Science and Engineering, Shenyang University of Technology, Shenyang, 110870, China

    Zhongda Tian

Authors
  1. Zhongda Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhongda Tian.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tian, Z. Echo state network based on improved fruit fly optimization algorithm for chaotic time series prediction. J Ambient Intell Human Comput 13, 3483–3502 (2022). https://doi.org/10.1007/s12652-020-01920-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12652-020-01920-4

Keywords

Search

Navigation