Analysis of an ND-policy Geo/G/1 queue and its application to wireless sensor networks | Operational Research Skip to main content
Springer Nature Link
Log in

Analysis of an ND-policy Geo/G/1 queue and its application to wireless sensor networks

  • Original Paper
  • Published:
Operational Research Aims and scope Submit manuscript

Abstract

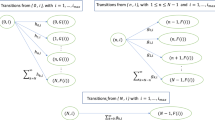
In this paper, we consider a discrete-time Geo/G/1 queue controlled by the combination of the N and D policies (called ND-policy). In this system, when there are N waiting customers or the service time backlog of all waiting customers exceeds a given threshold D, whichever emerges first, the idle server immediately resumes its service. Under this policy, since the service times of the customers arriving during the idle period, conditioned on the number of these customers, are dependent, and stochastically different from the service times of the customers arriving during the busy period, the customers in the system are classified into two types. Based on this classification, we first derive the probability generating functions and means of the queue length, idle and busy periods, service time backlog, waiting time and sojourn time, where the busy period is first studied in the discrete-time queues involving the D-policy. Next, by analyzing some results and flaws in the work of Gu et al. (J Syst Sci Complex, 2016. doi:10.1007/s11424-016-4180-y), we theoretically show the discrepancies that could arise if the conditional dependency of the service times of the customers arriving during the idle period is ignored. Finally, the numerical examples are provided to study the effects of different parameters on the mean queue length. Through an energy consumption optimization problem in wireless sensor networks, the application of our queueing model in the real world is illustrated, and the flaws that resulted from the results by Gu et al. (J Syst Sci Complex, 2016. doi:10.1007/s11424-016-4180-y) are numerically revealed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Agarwal RP, Dshalalow JH (2005) New fluctuation analysis of D-policy bulk queues with multiple vacations. Math Comput Model 41:253–269

    Article  Google Scholar 

  • Artalejo JR (2001) On the M/G/1 queue with D-policy. Appl Math Model 25:1055–1069

    Article  Google Scholar 

  • Balachandran KR (1973) Control policies for a single server system. Manag Sci 19:1013–1018

    Article  Google Scholar 

  • Balachandran KR, Tijms H (1975) On the D-policy for the M/G/1 queue. Manag Sci 21:1073–1076

    Article  Google Scholar 

  • Boxma OJ (1976) Note on a control problem of Balachandran and Tijms. Manag Sci 22:916–917

    Article  Google Scholar 

  • Dshalalow JH (1996) On applications of excess level processes to (N, D)-policy bulk queueing systems. J Appl Math Stoch Anal 9:551–562

    Article  Google Scholar 

  • Dshalalow JH (1998) Queueing processes in bulk systems under D-policy. J Appl Probab 35:976–989

    Article  Google Scholar 

  • Fuhrmann SW, Cooper RB (1985) Stochastic decompositions in the M/G/1 queue with generalized vacations. Oper Res 33(5):1117–1129

    Article  Google Scholar 

  • Gaki GK, Rhee HK, Sivazlian BD (1995) Distributions and first moments of the busy and idle periods in controllable M/G/1 queueing models with pure and dyadic policies. Stoch Anal Appl 13:47–81

    Article  Google Scholar 

  • Gu JX, Wei YY, Tang YH, Yu MM (2016) Queue size distribution of Geo/G/1 queue under the Min(N, D)-policy. J Syst Sci Complex. doi:10.1007/s11424-016-4180-y

  • Hernández-Díaz AG, Moreno P (2009) A discrete-time single-server queueing system with an N-policy, an early setup and a generalization of the bernoulli feedback. Math Comput Model 49:977–990

    Article  Google Scholar 

  • Hunter J (1983) Mathematical techniques of applied probability, discrete time models: techniques and applications, vol 2. Academic Press, New York

    Google Scholar 

  • Jiang FC, Huang DC, Yang CT, Leu FY (2012) Lifetime elongation for wireless sensor network using queue-based approaches. J Supercomput 59:1312–1335

    Article  Google Scholar 

  • Lan SJ, Tang YH (2016) Analysis of a discrete-time Geo\(^{\lambda _1,\lambda _2}\)/G/1 queue with N-policy and D-policy. J Appl Math Comput. doi:10.1007/s12190-016-0987-x

    Google Scholar 

  • Lee HW, Lee SW, Seo WJ, Cheon SH, Jeon J (2006) A unified framework for the analysis of the M/G/1 queues controlled by workload. Lect Note Comput Sci 3982:718–727

    Article  Google Scholar 

  • Lee SW, Lee HW, Baek JW (2011) Analysis of discrete-time Geo/G/1 queue under the D-policy. In: Proceedings of the 6th international conference on queueing theory and network applications. pp 107–115

  • Lee HW, Seo WJ, Lee SW, Jeon J (2010) Analysis of the MAP/G/1 queue under the Min(N, D)-policy. Stoch Models 26:98–123

    Article  Google Scholar 

  • Lee SW, Lee HW, Baek JW (2012) Analysis of discrete-time MAP/G/1 queue under workload control. Perform Eval 69:71–85

    Article  Google Scholar 

  • Lee HW, Seo WJ (2008) The performance of the M/G/1 queue under the dyadic Min(N, D)-policy and its cost optimization. Perform Eval 65:742–758

    Article  Google Scholar 

  • Lee DH, Yang WS (2013) The N-policy of a discrete time Geo/G/1 queue with disasters and its application to wireless sensor networks. Appl Math Model 37:9722–9731

    Article  Google Scholar 

  • Lim DE, Lee DH, Yang WS, Chae KC (2013) Analysis of the GI/Geo/1 queue with N-policy. Appl Math Model 37:4643–4652

    Article  Google Scholar 

  • Luo CY, Tang YH, Li W, Xiang KL (2012) The recursive solution of queue length for Geo/G/1 queue with N-policy. J Syst Sci Complex 25:293–302

    Article  Google Scholar 

  • Moreno P (2007) A discrete-time single-server queue with a modified N-policy. Int J Syst Sci 38:483–492

    Article  Google Scholar 

  • Moreno P (2008) Analysis of a Geo/G/1 queueing system with a generalized N-policy and setup-closedown times. Qual Technol Quant Manag 5:111–128

    Article  Google Scholar 

  • Rhee HK (1997) Development of a newmethodology to find the expected busy periods for controllable M/G/1 queueing models operating under the multivariable operating policies: concepts and applications to the dyadic policies. J Korean Inst Ind Eng 23:729–739

    Google Scholar 

  • Shanthikumar JG (1988) On stochastic decomposition in M/G/1 type queues with generalized server vacations. Oper Res 36(4):566–569

    Article  Google Scholar 

  • Tadj L, Choudhury G (2005) Optimal design and control of queues. Top 13:359–412

    Article  Google Scholar 

  • Takagi H (1993) Queueing analysis: vol III, discrete-time systems. North-Holland, Amsterdam

    Google Scholar 

  • Tijms HC (1976) Optimal control of workload in M/G/1 queueing system with removable server. Math Oper Stat Ser Stat 7:933–943

    Article  Google Scholar 

  • Wang TY, Ke JC (2009) The randomized threshold for the discrete-time Geo/G/1 queue. Appl Math Model 33:3178–3185

    Article  Google Scholar 

  • Wei YY, Yu MM, Tang YH, Gu JX (2012) Queue size distribution and capacity optimum design for N-policy Geo\(^{(\lambda _1,\lambda _2,\lambda _3)}/G/1\) queue with setup time and variable input rate. Math Comput Model 57:1559–1571

    Article  Google Scholar 

  • Yadin M, Naor P (1963) Queueing systems with a removable service station. Oper Res Q 14:393–405

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous reviewers for their valuable comments and suggestions to improve the quality of this paper. This research was supported in part by the NRF funds for the SARChI Chair in Advanced Sensor Networks (South Africa) and the National Natural Science Foundation of China (No. 71301111).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Chongqing University of Technology, Chongqing, 400054, China

    Renbin Liu

  2. Department of Electrical, Electronic and Computer Engineering, University of Pretoria, Pretoria, 0002, South Africa

    Renbin Liu & Attahiru Sule Alfa

  3. Department of Electrical and Computer Engineering, University of Manitoba, Winnipeg, MB, R3T 5V6, Canada

    Attahiru Sule Alfa

  4. School of Science, Sichuan University of Science and Engineering, Zigong, 643000, Sichuan, China

    Miaomiao Yu

Authors
  1. Renbin Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Attahiru Sule Alfa
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Miaomiao Yu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Renbin Liu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, R., Alfa, A.S. & Yu, M. Analysis of an ND-policy Geo/G/1 queue and its application to wireless sensor networks. Oper Res Int J 19, 449–477 (2019). https://doi.org/10.1007/s12351-017-0304-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12351-017-0304-y

Keywords

Mathematics Subject Classification