Time-space spectral Galerkin method for time-fractional fourth-order partial differential equations | Journal of Applied Mathematics and Computing Skip to main content
Springer Nature Link
Log in

Time-space spectral Galerkin method for time-fractional fourth-order partial differential equations

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

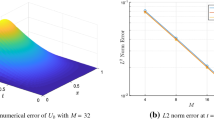
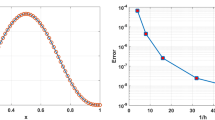
The goal of this paper is to present a high-order numerical scheme for solving fourth-order time-fractional partial differential equations (TFPDEs). The fractional derivative in the considered model is in Caputo’s sense. In the proposed approach, the time variable is approximated by the Legendre polynomials, and space discretisation is based on the modified basis constructed from a combination of the Legendre polynomials. We study the stability and convergence of the proposed method. Some numerical examples are investigated to validate the efficiency, accuracy, and theoretical results of the given method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Arqub, O.A.: Application of residual power series method for the solution of time-fractional Schrödinger equations in one-dimensional space. Fund. Inform. 166(2), 87–110 (2019)

    MathSciNet  MATH  Google Scholar 

  2. An, X., Liu, F., Zheng, M., Anh, V.V., Turner, I.W.: A space-time spectral method for time-fractional Black-Scholes equation. Appl. Numer. Math. 165, 152–166 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  3. Bu, W., Xiao, A., Zeng, W.: Finite difference/finite element methods for distributed-order time fractional diffusion equations. J. Sci. Comput. 72(1), 422–441 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  4. Canuto, C., Hussaini, M.Y., Quarteroni, A., Zang, T.A.: Spectral Methods: Fundamentals in Single Domains. Springer (2007)

  5. Cen, D., Wang, Z., Mo, Y.: Second order difference schemes for time-fractional KdV-Burgers’ equation with initial singularity. Appl. Math. Lett. 112, 106829 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  6. Chen, H., Lü, S., Chen, W.: Finite difference/spectral approximations for the distributed order time fractional reaction-diffusion equation on an unbounded domain. J. Comput. Phys. 315, 84–97 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chen, Y., Zhou, J.: Error estimates of spectral Legendre-Galerkin methods for the fourth-order equation in one dimension. Appl. Math. Comput. 268, 1217–1226 (2015)

    MathSciNet  MATH  Google Scholar 

  8. Dehghan, M., Safarpoor, M., Abbaszadeh, M.: Two high-order numerical algorithms for solving the multi-term time fractional diffusion-wave equations. J. Comput. Appl. Math. 290, 174–195 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  9. Dehghan, M., Abbaszadeh, M., Mohebbi, A.: Legendre spectral element method for solving time fractional modified anomalous sub-diffusion equation. Appl. Math. Model. 40(5–6), 3635–3654 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  10. Du, Y., Liu, Y., Li, H., Fang, Z., He, S.: Local discontinuous Galerkin method for a nonlinear time-fractional fourth-order partial differential equation. J. Comput. Phys. 344, 108–126 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  11. Ervin, V.J., Roop, J.P.: Variational formulation for the stationary fractional advection dispersion equation. Numer. Methods Partial Differ. Equ.: Int. J. 22(3), 558–576 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  12. Farhad, F.-I.: Fully spectral-Galerkin method for the one-and two-dimensional fourth-order time-fractional partial integro-differential equations with a weakly singular kernel. Numer. Methods Partial Differ. Equ. (2020). https://doi.org/10.1002/num.22634

  13. Fakhar-Izadi, F.: Fully Petrov-Galerkin spectral method for the distributed-order time-fractional fourth-order partial differential equation. Eng. Comput. 1–10 (2020b)

  14. Gao, G., Alikhanov, A.A., Sun, Z.: The temporal second order difference schemes based on the interpolation approximation for solving the time multi-term and distributed-order fractional sub-diffusion equations. J. Sci. Comput. 73(1), 93–121 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  15. Guo, L., Wang, Z., Vong, S.: Fully discrete local discontinuous Galerkin methods for some time-fractional fourth-order problems. Int. J. Comput. Math. 93(10), 1665–1682 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  16. Hao, Z., Sun, Z., Cao, W.: A fourth-order approximation of fractional derivatives with its applications. J. Comput. Phys. 281, 787–805 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  17. Hu, X., Zhang, L.: A compact finite difference scheme for the fourth-order fractional diffusion-wave system. Comput. Phys. Commun. 182(8), 1645–1650 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  18. Hu, X., Zhang, L.: A new implicit compact difference scheme for the fourth-order fractional diffusion-wave system. Int. J. Comput. Math. 91(10), 2215–2231 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  19. Jafari, H., Dehghan, M., Sayevand, K.: Solving a fourth-order fractional diffusion-wave equation in a bounded domain by decomposition method. Numer. Methods Partial Differ. Equ. Int. J. 24(4), 1115–1126 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  20. Kharazmi, E., Zayernouri, M., Karniadakis, G.E.: Petrov-Galerkin and spectral collocation methods for distributed order differential equations. SIAM J. Sci. Comput. 39(3), A1003–A1037 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  21. Kilbas, A.A., Marichev, O.I., Samko, S.G.: Fractional Integral and Derivatives: Theory and Applications. Gordon and Breach, Switzerland (1993)

    MATH  Google Scholar 

  22. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations, Vol. 204. Elsevier (2006)

  23. Li, H., Jiang, W., Li, W.: Space-time spectral method for the Cattaneo equation with time fractional derivative. Appl. Math. Comput. 349, 325–336 (2019)

    MathSciNet  MATH  Google Scholar 

  24. Li, X., Chuanju, X.: A space-time spectral method for the time fractional diffusion equation. SIAM J. Numer. Anal. 47(3), 2108–2131 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  25. Li, X., Chuanju, X.: Existence and uniqueness of the weak solution of the space-time fractional diffusion equation and a spectral method approximation. Commun. Comput. Phys. 8(5), 1016 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  26. Liu, Y., Fang, Z., Li, H., He, S.: A mixed finite element method for a time-fractional fourth-order partial differential equation. Appl. Math. Comput. 243, 703–717 (2014)

    MathSciNet  MATH  Google Scholar 

  27. Miller, K.S., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley (1993)

  28. Momani, S., Abu Arqub, O., Maayah, B.: Piecewise optimal fractional reproducing kernel solution and convergence analysis for the Atangana-Baleanu-Caputo model of the Lienard’s equation. Fractals 28(08), 2040007 (2020)

    Article  MATH  Google Scholar 

  29. Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, Vol. 198. Elsevier (1998)

  30. Qiao, L., Wang, Z., Da, X.: An alternating direction implicit orthogonal spline collocation method for the two dimensional multi-term time fractional integro-differential equation. Appl. Numer. Math. 151, 199–212 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  31. Ran, M., Zhang, C.: New compact difference scheme for solving the fourth-order time fractional sub-diffusion equation of the distributed order. Appl. Numer. Math. 129, 58–70 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  32. Roul, P., Goura, V.M.K.P.: A high order numerical method and its convergence for time-fractional fourth order partial differential equations. Appl. Math. Comput. 366, 124727 (2020)

    MathSciNet  MATH  Google Scholar 

  33. Sayevand, K., Yazdani, A., Arjang, F.: Cubic B-spline collocation method and its application for anomalous fractional diffusion equations in transport dynamic systems. J. Vib. Control 22(9), 2173–2186 (2016)

  34. Shen, J., Wang, L.-L.: Fourierization of the Legendre-Galerkin method and a new space-time spectral method. Appl. Numer. Math. 57(5–7), 710–720 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  35. Shen, J., Tang, T., Wang, L.-L.: Spectral Methods: Algorithms, Analysis and Applications, Vol. 41. Springer (2011)

  36. Sheng, C., Shen, J.: A space-time Petrov-Galerkin spectral method for time fractional diffusion equation. Numer. Math. Theory Methods Appl. 11(4) (2018)

  37. Siddiqi, S.S., Arshed, S.: Numerical solution of time-fractional fourth-order partial differential equations. Int. J. Comput. Math. 92(7), 1496–1518 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  38. Szegö, G.: Orthogonal Polynomials, Vol. 23. In: American Mathematical Society Colloquium Publications (1975)

  39. Tariq, H., Akram, G.: Quintic spline technique for time fractional fourth-order partial differential equation. Numer. Methods Partial Differ. Equ. 33(2), 445–466 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  40. Vong, S., Wang, Z.: Compact finite difference scheme for the fourth-order fractional sub-diffusion system. Adv. Appl. Math. Mech. 6(4), 419–435 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  41. Wang, Z., Cen, D., Mo, Y.: Sharp error estimate of a compact L1-ADI scheme for the two-dimensional time-fractional integro-differential equation with singular kernels. Appl. Numer. Math. 159, 190–203 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  42. Wei, L., He, Y.: Analysis of a fully discrete local discontinuous Galerkin method for time-fractional fourth-order problems. Appl. Math. Model. 38(4), 1511–1522 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  43. Zhe, Yu., Boying, W., Sun, J.: A space-time spectral method for one-dimensional time fractional convection diffusion equations. Math. Methods Appl. Sci. 40(7), 2634–2648 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  44. Zhang, C., Yao, H., Li, H.: New space-time spectral and structured spectral element methods for high order problems. J. Comput. Appl. Math. 351, 153–166 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  45. Zhao, Z., Jin, X.-Q., Lin, M.M.: Preconditioned iterative methods for space-time fractional advection-diffusion equations. J. Comput. Phys. 319, 266–279 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  46. Zheng, M., Liu, F., Anh, V., Turner, I.: A high-order spectral method for the multi-term time-fractional diffusion equations. Appl. Math. Model. 40(7–8), 4970–4985 (2016)

  47. Zheng, M., Liu, F., Turner, I., Anh, V.: A novel high order space-time spectral method for the time fractional Fokker-Planck equation. SIAM J. Sci. Comput. 37(2), A701–A724 (2015)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Computer Science, Amirkabir University of Technology (Tehran Polytechnic), Tehran, Iran

    Farhad Fakhar-Izadi & Narges Shabgard

Authors
  1. Farhad Fakhar-Izadi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Narges Shabgard
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fakhar-Izadi, F., Shabgard, N. Time-space spectral Galerkin method for time-fractional fourth-order partial differential equations. J. Appl. Math. Comput. 68, 4253–4272 (2022). https://doi.org/10.1007/s12190-022-01707-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-022-01707-0

Keywords

Mathematics Subject Classification

Search

Navigation