A method for fuzzy time series forecasting based on interval index number and membership value using fuzzy c-means clustering | Evolutionary Intelligence Skip to main content
Springer Nature Link
Log in

A method for fuzzy time series forecasting based on interval index number and membership value using fuzzy c-means clustering

  • Research Paper
  • Published:
Evolutionary Intelligence Aims and scope Submit manuscript

Abstract

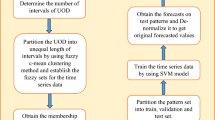
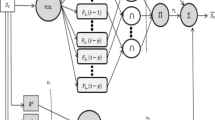
Fuzzy time series forecasting methods are very popular among researchers for predicting future values as they are not based on the strict assumptions of traditional forecasting methods. Non-stochastic methods of fuzzy time series forecasting are preferred by the researchers over the years because these methods are capable to deal with real life uncertainties and provide significant forecast. There are generally, four factors that determine the performance of the forecasting method (1) number of intervals (NOIs) and length of intervals to partition universe of discourse (UOD), (2) fuzzification rules or feature representation of crisp time series, (3) method of establishing fuzzy logic rule (FLRs), (4) defuzzification rule to get crisp forecasted value. Considering, first two factors to improve the forecasting accuracy, we proposed a modified non-stochastic method of fuzzy time series forecasting in which interval index number and membership value are used as input features to predict future value. We suggested a rounding-off range and large step-size method to find the optimal NOIs and used fuzzy c-means clustering process to divide UOD into intervals of unequal length. We implement two techniques (1) regression by support vector machine and (2) neural network by multilayer perceptron to establish FLRs. To test our proposed method by both techniques we conduct a simulated study on eight widely used real time series and compare the performance with some recently developed models. Two performance measures RSME and SMAPE are used for performance analysis and observed better forecasting accuracy by the proposed model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353. https://doi.org/10.1016/S0019-9958(65)90241-X

    Article  MATH  Google Scholar 

  2. Song Q, Chissom BS (1993) Forecasting enrollments with fuzzy time series—part I. Fuzzy Sets Syst 54(1):1–9. https://doi.org/10.1016/0165-0114(93)90355-L

    Article  Google Scholar 

  3. Song Q, Chissom BS (1993) Fuzzy time series and its models. Fuzzy Sets Syst 54(3):269–277. https://doi.org/10.1016/0165-0114(93)90372-O

    Article  MATH  Google Scholar 

  4. Song Q, Chissom BS (1994) Forecasting enrollments with fuzzy time series—part II. Fuzzy Sets Syst 62(1):1–8. https://doi.org/10.1016/0165-0114(94)90067-1

    Article  Google Scholar 

  5. Chen SM (1996) Forecasting enrollments based on fuzzy time series. Fuzzy Sets Syst 81(3):311–319. https://doi.org/10.1016/0165-0114(95)00220-0

    Article  Google Scholar 

  6. Huarng K (2001) Effective lengths of intervals to improve forecasting in fuzzy time series. Fuzzy Sets Syst 123(3):387–394. https://doi.org/10.1016/S0165-0114(00)00057-9

    Article  MATH  Google Scholar 

  7. Huarng K (2001) Heuristic models of fuzzy time series for forecasting. Fuzzy Sets Syst 123(3):369–386. https://doi.org/10.1016/S0165-0114(00)00093-2

    Article  MATH  Google Scholar 

  8. Li ST, Cheng YC (2007) Deterministic fuzzy time series model for forecasting enrollments. Comput Math Appl 53:1904–1920. https://doi.org/10.1016/j.camwa.2006.03.036

    Article  MATH  Google Scholar 

  9. Huarng K, Yu THK (2006) Ratio-based lengths of intervals to improve fuzzy time series forecasting. IEEE Trans Syst Man Cybern B Cybern 36(2):328–340. https://doi.org/10.1109/TSMCB.2005.857093

    Article  Google Scholar 

  10. Chen SM, Chung NY (2006) Forecasting enrollments using high-order fuzzy time series and genetic algorithms. Int J Intell Syst 21:485–501. https://doi.org/10.1002/int.20145

    Article  MATH  Google Scholar 

  11. Yu T (2005) A Refined Fuzzy Time-Series Model for Forecasting. Physica A 346:657–681. https://doi.org/10.1016/j.physa.2004.07.024

    Article  Google Scholar 

  12. Kuo IH, Horng SJ, Kao TW, Lin TL, Lee CL, Pan Y (2009) An improved method for forecasting enrollments based on fuzzy time series and particle swarm optimization. Expert Syst Appl 36:6108–6117. https://doi.org/10.1016/j.eswa.2008.07.043

    Article  Google Scholar 

  13. Kuo IH, Horng SJ, Chen YH, Run RS, Kao TW, Chen RJ, Lai JL, Lin TL (2010) Forecasting TAIFEX based on fuzzy time series and particle swarm optimization. Expert Syst Appl 37:1494–1502. https://doi.org/10.1016/j.eswa.2009.06.102

    Article  Google Scholar 

  14. Hsu LY, Horng SJ, Kao TW, Chen YH, Run RS, Chen RJ, Lai JL, Kuo IH (2010) Temperature prediction and TAIFEX forecasting based on fuzzy relationships and MTPSO techniques. Expert Syst Appl 37:2756–2770. https://doi.org/10.1016/j.eswa.2009.09.015

    Article  Google Scholar 

  15. Huang YL, Horng SJ, He M, Fan P, Kao TW, Khan MK, Lai JL, Kuo IH (2011) A hybrid forecasting model for enrollments based on aggregated fuzzy time series and particle swarm optimization. Expert Syst Appl 38:8014–8023. https://doi.org/10.1016/j.eswa.2010.12.127

    Article  Google Scholar 

  16. Chen SM, Phuong BDH (2017) Fuzzy time series forecasting based on optimal partitions of intervals and optimal weighting vectors. Knowl-Based Syst 118:204–216. https://doi.org/10.1016/j.knosys.2016.11.019

    Article  Google Scholar 

  17. Cai Q, Zhang D, Zheng W, Leung SC (2015) A new fuzzy time series forecasting model combined with ant colony optimization and auto-regression. Knowl Based Syst 74:61–68. https://doi.org/10.1016/j.knosys.2014.11.003

    Article  Google Scholar 

  18. Enayatifar R, Sadaei HJ, Abdullah AH, Gani A (2013) Imperialist competitive algorithm combined with refined high-order weighted fuzzy time series (RHWFTS-ICA) for short term load forecasting. Energy Convers Manag 76:1104–1116. https://doi.org/10.1016/j.enconman.2013.08.039

    Article  Google Scholar 

  19. Sadaei HJ, Enayatifar R, Lee MH, Mahmud M (2016) A hybrid model based on differential fuzzy logic relationships and imperialist competitive algorithm for stock market forecasting. Appl Soft Comput J 40:132–149. https://doi.org/10.1016/j.asoc.2015.11.026

    Article  Google Scholar 

  20. Bisht K, Kumar S (2016) Fuzzy time series forecasting method based on hesitant fuzzy sets. Expert Syst Appl 64:557–568. https://doi.org/10.1016/j.eswa.2016.07.044

    Article  Google Scholar 

  21. Gupta K, Kumar S (2018) Hesitant probabilistic fuzzy set based time series forecasting method. Granul Comput 4:739–758. https://doi.org/10.1007/s41066-018-0126-1

    Article  Google Scholar 

  22. Cheng CH, Cheng GW, Wang JW (2008) Multi-attribute fuzzy time series method based on fuzzy clustering. Expert Syst Appl 34:1235–1242. https://doi.org/10.1016/j.eswa.2006.12.013

    Article  Google Scholar 

  23. Li ST, Cheng YC, Lin SY (2008) A FCM-based deterministic forecasting model for fuzzy time series. Comput Math Appl 56:3052–3063. https://doi.org/10.1016/j.camwa.2008.07.033

    Article  MATH  Google Scholar 

  24. Liu HT, Wei ML (2010) An improved fuzzy forecasting method for seasonal time series. Expert Syst Appl 37:6310–6318. https://doi.org/10.1016/j.eswa.2010.02.090

    Article  Google Scholar 

  25. Pattanayak RM, Panigrahi S, Behera HS (2020) High-order fuzzy time series forecasting by using membership values along with data and support vector machine. Arab J Sci Eng. https://doi.org/10.1007/s13369-020-04721-1

    Article  Google Scholar 

  26. Egrioglu E, Aladag CH, Yolcu U, Uslu VR, Erilli NA (2011) Fuzzy time series forecasting method based on Gustafson–Kessel fuzzy clustering. Expert Syst Appl 38:10355–10357. https://doi.org/10.1016/j.eswa.2011.02.052

    Article  Google Scholar 

  27. Cheng CH, Chang JR, Yeh CA (2006) Entropy-based and trapezoid fuzzification-based fuzzy time series approaches for forecasting IT project cost. Technol Forecast Soc Change 73:524–542. https://doi.org/10.1016/j.techfore.2005.07.004

    Article  Google Scholar 

  28. Rubio A, Bermúdez JD, Vercher E (2016) Forecasting portfolio returns using weighted fuzzy time series methods. Int J Approx Reason 75:1–12. https://doi.org/10.1016/j.ijar.2016.03.007

    Article  MATH  Google Scholar 

  29. Rubio A, Bermúdez JD, Vercher E (2017) Improving stock index forecasts by using a new weighted fuzzy-trend time series method. Expert Syst Appl 76:12–20. https://doi.org/10.1016/j.eswa.2017.01.049

    Article  Google Scholar 

  30. Yolcu OC, Yolcu U, Egrioglu E, Aladag CH (2016) High order fuzzy time series forecasting method based on an intersection operation. Appl Math Model 40:8750–8765. https://doi.org/10.1016/j.apm.2016.05.012

    Article  MATH  Google Scholar 

  31. Tinh NV (2020) Enhanced forecasting accuracy of fuzzy time series model based on combined fuzzy C-mean clustering with particle swam optimization. Int J Comput Intell Appl. https://doi.org/10.1142/S1469026820500170

    Article  Google Scholar 

  32. Iqbal S, Zhang C, Arif M, Hassan M, Ahmad S (2020) A new fuzzy time series forecasting method based on clustering and weighted average approach. J Intell Fuzzy Syst 38(5):6089–6098. https://doi.org/10.3233/JIFS-179693

    Article  Google Scholar 

  33. Aladag CH, Yolcu U, Egrioglu E, Dalar AZ (2012) A new time invariant fuzzy time series forecasting method based on particle swarm optimization. Appl Soft Comput J 12:3291–3299. https://doi.org/10.1016/j.asoc.2012.05.002

    Article  Google Scholar 

  34. Wong HL, Tu YH, Wang CC (2010) Application of fuzzy time series models for forecasting the amount of Taiwan export. Expert Syst Appl 37:1465–1470. https://doi.org/10.1016/j.eswa.2009.06.106

    Article  Google Scholar 

  35. Singh P, Borah B (2013) An efficient time series forecasting model based on fuzzy time series. Eng Appl Artif Intell 26:2443–2457. https://doi.org/10.1016/j.engappai.2013.07.012

    Article  Google Scholar 

  36. Ye F, Zhang L, Zhang D, Fujita H, Gong Z (2016) A novel forecasting method based on multi-order fuzzy time series and technical analysis. Inf Sci 367–368:41–57. https://doi.org/10.1016/j.ins.2016.05.038

    Article  MATH  Google Scholar 

  37. Cheng SH, Chen SM, Jian WS (2016) Fuzzy time series forecasting based on fuzzy logical relationships and similarity measures. Inf Sci 327:272–287. https://doi.org/10.1016/j.ins.2015.08.024

    Article  MATH  Google Scholar 

  38. Loia V, Tomasiello S, Vaccaro A, Gao J (2020) Using local learning with fuzzy transform: application to short term forecasting problems. Fuzzy Optim Decis Mak 19(1):13–32. https://doi.org/10.1007/s10700-019-09311-x

    Article  MATH  Google Scholar 

  39. Nguyen L, Novák V (2019) Forecasting seasonal time series based on fuzzy techniques. Fuzzy Sets Syst 361:114–129. https://doi.org/10.1016/J.FSS.2018.09.010

    Article  MATH  Google Scholar 

  40. Huarng K, Yu THK (2006) The application of neural networks to forecast fuzzy time series. Physica A 363:481–491. https://doi.org/10.1016/j.physa.2005.08.014

    Article  Google Scholar 

  41. Aladag CH, Basaran MA, Egrioglu E, Yolcu U, Uslu VR (2009) Forecasting in high order fuzzy times series by using neural networks to define fuzzy relations. Expert Syst Appl 36:4228–4231. https://doi.org/10.1016/j.eswa.2008.04.001

    Article  Google Scholar 

  42. Egrioglu E, Aladag CH, Yolcu U, Uslu VR, Basaran MA (2009) A new approach based on artificial neural networks for high order multivariate fuzzy time series. Expert Syst Appl 36:10589–10594. https://doi.org/10.1016/j.eswa.2009.02.057

    Article  Google Scholar 

  43. Singh P, Borah B (2013) High-order fuzzy-neuro expert system for time series forecasting. Knowl Based Syst 46:12–21. https://doi.org/10.1016/j.knosys.2013.01.030

    Article  Google Scholar 

  44. Gu L, Guo H, Liu X (2017) Fuzzy time series forecasting based on information granule and neural network. Int J Comput Sci Eng 15(1–2):146–152. https://doi.org/10.1504/IJCSE.2017.085968

    Article  Google Scholar 

  45. Bas E, Grosan C, Egrioglu E, Yolcu U (2018) High order fuzzy time series method based on pi-sigma neural network. Eng Appl Artif Intell 72:350–356. https://doi.org/10.1016/j.engappai.2018.04.017

    Article  Google Scholar 

  46. Panigrahi S, Behera DH (2018) A computationally efficient method for high order fuzzy time series forecasting. J Theor Appl Inf Technol 96:7215–7226

    Google Scholar 

  47. Panigrahi S, Behera HS (2020) A study on leading machine learning techniques for high order fuzzy time series forecasting. Eng Appl Artif Intell 87:103245. https://doi.org/10.1016/j.engappai.2019.103245

    Article  Google Scholar 

  48. Bezdek JC (1981) Pattern recognition with fuzzy objective function algorithms. Springer, Boston. https://doi.org/10.1007/978-1-4757-0450-1

  49. Vapnik VN (1995) The nature of statistical learning theory. Springer, New York. https://doi.org/10.1007/978-1-4757-2440-0

  50. Aladag C (2013) Using multiplicative neuron model to establish fuzzy logic relationships. Expert Syst Appl 40:850–853. https://doi.org/10.1016/j.eswa.2012.05.039

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Statistics and Computer Science, G. B. Pant University of Agriculture and Technology, Pantnagar, Uttarakhand, 263145, India

    Kiran Bisht & Arun Kumar

Authors
  1. Kiran Bisht
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Arun Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kiran Bisht.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bisht, K., Kumar, A. A method for fuzzy time series forecasting based on interval index number and membership value using fuzzy c-means clustering. Evol. Intel. 16, 285–297 (2023). https://doi.org/10.1007/s12065-021-00656-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12065-021-00656-0

Keywords

Search

Navigation