Abstract
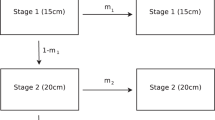
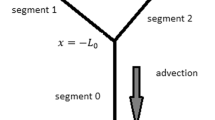
We use a reaction diffusion equation, together with a genetic algorithm approach for model selection to develop a general modeling framework for biological invasions. The diffusion component of the reaction diffusion model is generalized to include dispersal and advection. The reaction component is generalized to include both linear and non-linear density dependence, and Allee effect. A combination of the reaction diffusion and genetic algorithm is able to evolve the most parsimonious model for invasive species spread. Zebra mussel data obtained from Lake Champlain, which demarcates the states of New York and Vermont, is used to test the appropriateness of the model. We estimate the minimum wave spread rate of Zebra mussels to be 22.5 km/year. In particular, the evolved models predict an average northward advection rate of 60.6 km/year (SD ± 1.9), which compares very well with the rate calculated from the known hydrologic residence time of 60 km/year. A combination of a reaction diffusion model and a genetic algorithm is, therefore, able to adequately describe some of the hydrodynamic features of Lake Champlain and the spread of a typical invasive species—Zebra mussels within the lake.


Similar content being viewed by others
References
Akaike H (1973) Information theory and an extension of maximum likelihood Principle. In: Petrov BN, Csaki F (eds) Second international symposium on information theory. Akademia Kiado, Budapest, pp 267–281
Andow DA, Kareiva PM, Levin SA, Okubo A (1990) Spread of invading organisms. Landsc Ecol 4:177–188
Bentil DE, Osei BM, Ellingwood CD, Hoffmann JP (2003) Uncertainty modeling and analysis. In: 4th International Symposium on Uncertainty Modeling and Analysis (ISUMA), College Park, MD
Bentil DE, Osei BM, Ellingwood CD, Hoffmann JP (2007) Analysis of a Schnute postulate-based unified growth model for mode selection in evolutionary computations. BioSystems 90:467–474
Flockhart W, Radcliffe NJ (1995) GA-MINER: parallel data mining with hierarchical genetic algorithms. Final Report, The University of Edinburgh
Hauser M, Gustavsen L (1998) Zebra mussels. In: Otter T, Soper E (eds) Lake Champlain basin program: facts series 1. http://lcbp.org/factsht/zmfs.PDF
Hoffman JP (2006) Simultaneous inductive and deductive modeling of ecological systems via evolutionary computation and information theory. Simulation 82(7):439–450
Hoffmann JP, Ellingwood CD, Osei BM, Bentil DE (2004) Ecological model selection via evolutionary computation and information theory. Genet Program Evolvable Mach 5(2):229–241
Horvath TG, Crane L (2010) Hydrodynamic forces affect larval zebra mussel (Dreissena polymorpha) mortality in a laboratory setting. Aquat Invasions 5(4). doi:10.3391/ai.2010.5.4
Kullback S, Leibler RA (1951) On information and sufficiency. Ann Math Stat 22:79–86
Levine D (1996) Users’ guide to the PGAPack parallel genetic algorithm library Technical Report ANL-95/18. Argonne National Laboratory, Batavia
Lubina JA, Levin SA (1988) The spread of a reinvading species in the California Sea Otter. Am Nat 131(4):526–543
Murray JD (2001) Mathematical biology. Springer-Verlag, Berlin
Osei BM, Hoffmann JP, Ellingwood CD, Bentil DE (2005) Probabilistic uncertainty in population dynamics. WSEAS Trans Biol Biomed 2(1):51–56
Pond SLK, Posada D, Gravenor MB, Woelk CH, Frost SDW (2006a) GARD: a genetic algorithm for recombination detection. Bioinformatics 22(24):3096–3098
Pond SLK, Posada D, Gravenor MB, Woelk CH, Frost SDW (2006b) Automated phylogenetic detection of recombination using a genetic algorithm. Mol Biol Evol 23(10):1891–1901
Pond SLK, Mannino FV, Gravenor MB, Muse SV, Frost SDW (2007) Evolutionary model selection with a genetic algorithm: a case study using stem RNA. Mol Biol Evol 24(1):159–170
Ross P, Tuson A (1998) Adapting operator settings in genetic algorithms. Evol Algorithm 6(2):161–184
Stoeckel JA, Rehmann CR, Schneider DW, Padilla DK (2004) Retention and supply of zebra mussel larvae in a large river system: importance of an upstream lake. Freshw Biol 49:919–930
Viard F, Ellien C, Dupont L (2006) Dispersal ability and invasion success of Crepidula fornicata in a single gulf: insights from genetic markers and larval-dispersal model. Helgoland Marine Res 60:144–152
Acknowledgments
This work was supported in part by grants from the National Science Foundation (DUE 0436330) to DEB; United States Department of Agriculture Hatch and the University of Vermont Department of Energy Computational Biology grants to JPH, and DEB and support from Eastern Connecticut State University to OBM
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Osei, B.M., Ellingwood, C.D., Hoffmann, J.P. et al. Modeling invasive species spread in Lake Champlain via evolutionary computations. Theory Biosci. 130, 145–152 (2011). https://doi.org/10.1007/s12064-011-0122-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12064-011-0122-3