Mixture modeling of data with multiple partial right-censoring levels | Advances in Data Analysis and Classification
Skip to main content
Springer Nature Link
Log in

Mixture modeling of data with multiple partial right-censoring levels

  • Regular Article
  • Published:
Advances in Data Analysis and Classification Aims and scope Submit manuscript

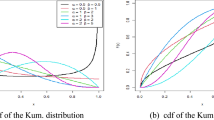
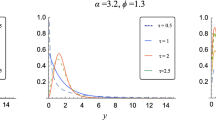
Abstract

In this paper, a new flexible approach to modeling data with multiple partial right-censoring points is proposed. This method is based on finite mixture models, flexible tool to model heterogeneity in data. A general framework to accommodate partial censoring is considered. In this setting, it is assumed that a certain portion of data points are censored and the rest are not. This situation occurs in many insurance loss data sets. A novel probability function is proposed to be used as a mixture component and the expectation-maximization algorithm is employed for estimating model parameters. The Bayesian information criterion is used for model selection. Additionally, an approach for the variability assessment of parameter estimates as well as the computation of quantiles commonly known as risk measures is considered. The proposed model is evaluated using a simulation study based on four common probability distribution functions used to model right skewed loss data and applied to a real data set with good results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
¥17,985 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price includes VAT (Japan)

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Bakar SA A, Hamzaha N A, Maghsoudia M, Nadarajah S (2015) Modeling loss data using composite models. Insur Math Econ 61:146–154

    Article  MathSciNet  Google Scholar 

  • Balakrishnan N, Mitra D (2011) Likelihood inference for lognormal data with left truncation and right censoring with an illustration. J Stat Plan Inference 141:3536–3553

    Article  MathSciNet  Google Scholar 

  • Balakrishnan N, Mitra D (2012) Left truncated and right censored Weibull data and likelihood inference with an illustration. Comput Stat Data Anal 56:4011–4025

    Article  MathSciNet  Google Scholar 

  • Balakrishnan N, Mitra D (2013) Likelihood inference based on left truncated and right censored data from a gamma distribution. IEEE Trans Reliab 62:679–688

    Article  Google Scholar 

  • Bang S, Cho H, Jhun M (2016) Simultaneous estimation for non-crossing multiple quantile regression with right censored data. Statistics and Computing 26:131–147

    Article  MathSciNet  Google Scholar 

  • Beirlant J, Goegebeur Y, Teugels J, Segers J (2004) Statistics of Extremes, 1st edn. Wiley, Hobuken, NJ

    Book  Google Scholar 

  • Biernacki C, Celeux G, Govaert G (2003) Choosing starting values for the EM algorithm for getting the highest likelihood in multivariate Gaussian mixture models. Comput Stat Data Anal 413:561–575

    Article  MathSciNet  Google Scholar 

  • Blostein M, Miljkovic T (2019a) ltmix: Left-Truncated Mixtures of Gamma. Weibull, and Lognormal Distributions, r package version (2)

  • Blostein M, Miljkovic T (2019) On modeling left-truncated loss data using mixtures of distributions. Insur Math Econ 85:35–46

    Article  MathSciNet  Google Scholar 

  • Bordes L, Chauveau D (2016) Stochastic EM algorithms for parametric and semiparametric mixture models for right-censored lifetime data. Comput Stat 31:1513–1538

    Article  MathSciNet  Google Scholar 

  • Calderín-Ojeda E, Kwok CF (2016) Modeling claims data with composite stoppa models. Scandinavian Actuarial Journal 9:817–836

    Article  MathSciNet  Google Scholar 

  • Chauveau D (1995) ‘A stochastic EM algorithm for mixture with censored data. J Stat Plan 46:1–25

    Article  MathSciNet  Google Scholar 

  • Coorey K, Ananda MM (2005) Modeling actuarial data with a composite Lognormal-Pareto model. Scandinavian Actuarial Journal 5:321–334

    Article  MathSciNet  Google Scholar 

  • Frees E, Valdez E (1998) Understanding relationships using copulas. N Am Actuar J 2:1–15

    Article  MathSciNet  Google Scholar 

  • Gruen B, Leisch F, Sarkar D, Mortier F (2019) ltmix: Left-Truncated Mixtures of Gamma, Weibull, and Lognormal Distributions, r package version 2.3-15

  • Gui W, Huang R, Lin XS (2018) Fitting the Erlang mixture model to data via a GEM-CMM algorithm. J Comput Appl Math 343:189–205

    Article  MathSciNet  Google Scholar 

  • Hoeting JA, Madigan D, Raftery AE, Volinsky CT (1999) Bayesian model averaging: a tutorial. Stat Sci 14:382–401

    Article  MathSciNet  Google Scholar 

  • Hubert L, Arabie P (1985) Comparing partitions. J Classif 2:193–218

    Article  Google Scholar 

  • Klugman S A, Panjer H H, Willmot G E (2012) Loss Models: From Data to Decisions, 4th edn. Wiley, Hobuken, NJ

    MATH  Google Scholar 

  • Klugman S A, Parsa R (1999) Fitting bivariate loss distribution with copulas. Insur Math Econ 24:139–148

    Article  MathSciNet  Google Scholar 

  • Lee G, Scott C (2012) EM algorithms for multivariate Gaussian mixture models with truncated and censored data. Comput Stat Data Anal 56:2816–2829

    Article  MathSciNet  Google Scholar 

  • Lee SCK, Lin XS (2010) Modeling and evaluating insurance losses via mixtures of Erlang distributions. N Am Actuar J 14:107–130

    Article  MathSciNet  Google Scholar 

  • McLachlan G, Jones SAA (1988) Fitting mixture models to grouped and truncated data via the EM algorithm. Biometrics 22:571–578

    Article  Google Scholar 

  • McLachlan G, Peel D (2000) Finite mixture models. Wiley, Hobuken, NJ

    Book  Google Scholar 

  • McNeil A (1997) Estimating the tails of loss severity distributions using extreme value theory. ASTIN Bull 27:117–137

    Article  Google Scholar 

  • Melnykov V, Michael S, Melnykov I (2015) Recent developments in model-based clustering with applications. In: Celebi ME (ed) Partitional clustering algorithms. Springer, Berlin, pp 1–39

    MATH  Google Scholar 

  • Michael S, Melnykov V (2016) An effective strategy for initializing the EM algorithm in finite mixture models. Adv Data Anal Classif 10:563–583

    Article  MathSciNet  Google Scholar 

  • Miljkovic T, Grün B (2016) Modeling loss data using mixtures of distributions. Insur Math Econ 70:387–396

    Article  MathSciNet  Google Scholar 

  • Pigeon M, Denuit M (2011) Composite Lognormal–Pareto Model with random threshold. Scandinavian Actuarial Journal 3:177–192

    Article  MathSciNet  Google Scholar 

  • R Core Team (2016) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria

  • Resnick SI (1997) Discussion of the Danish data on large fire insurance losses. ASTIN Bull 27:139–151

    Article  Google Scholar 

  • Ross S M (2014) Introduction to probability models, 11th edn. Academic Press, New York

    MATH  Google Scholar 

  • Schwarz G (1978) Estimating the dimension of a model. Ann Stat 6:461–464

    Article  MathSciNet  Google Scholar 

  • Scollnik DP (2007) On composite Lognormal-Pareto models. Scan Actuar J 1:20–33

    Article  MathSciNet  Google Scholar 

  • Sun Z, Ye X, Sun L (2018) Consistent test for parametric models with right-censored data using projections. Comput Stat Data Anal 118:112–125

    Article  MathSciNet  Google Scholar 

  • Verbelen R, Gong L, Antonio K, Badescu A, Lin S (2015) Fitting mixtures of Erlangs to censored and truncated data using the EM algorithm. ASTIN Bull 45:729–758

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, South Dakota State University, Brookings, SD, 57007, USA

    Semhar Michael

  2. Department of Statistics, Miami University, Oxford, OH, 45056, USA

    Tatjana Miljkovic

  3. Department of Information Systems, Statistics, and Management Science, University of Alabama, Tuscaloosa, AL, 35487, USA

    Volodymyr Melnykov

Authors
  1. Semhar Michael
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tatjana Miljkovic
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Volodymyr Melnykov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Semhar Michael.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 2096 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Michael, S., Miljkovic, T. & Melnykov, V. Mixture modeling of data with multiple partial right-censoring levels. Adv Data Anal Classif 14, 355–378 (2020). https://doi.org/10.1007/s11634-020-00391-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11634-020-00391-x

Keywords

Mathematics Subject Classification

Search

Navigation