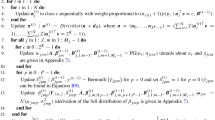Abstract
The evaluation of nursing homes is usually based on the administration of questionnaires made of a large number of polytomous items to their patients. In such a context, the latent class model represents a useful tool for clustering subjects in homogenous groups corresponding to different degrees of impairment of the health conditions. It is known that the performance of model-based clustering and the accuracy of the choice of the number of latent classes may be affected by the presence of irrelevant or noise variables. In this paper, we show the application of an item selection algorithm to a dataset collected within a project, named ULISSE, on the quality-of-life of elderly patients hosted in Italian nursing homes. This algorithm, which is closely related to that proposed by Dean and Raftery in 2010, is aimed at finding the subset of items which provides the best clustering according to the Bayesian Information Criterion. At the same time, it allows us to select the optimal number of latent classes. Given the complexity of the ULISSE study, we perform a validation of the results by means of a sensitivity analysis, with respect to different specifications of the initial subset of items, and of a resampling procedure.
Similar content being viewed by others
References
Bacci S, Bartolucci F, Gnaldi M (2014) A class of multidimensional latent class IRT models for ordinal polytomous item responses. Commun Stat Theory Methods 43:787–800
Bandeen-Roche K, Miglioretti DL, Zeger SL, Rathouz PJ (1997) Latent variable regression for multiple discrete outcomes. J Am Stat Assoc 92:1375–1386
Bandeen-Roche K, Xue QL, Ferrucci L, Walston J, Guralnik JM, Chaves P, Zeger SL, Fried LP (2006) Phenotype of frailty: characterization in the women’s health and aging studies. J Gerontol Ser A Biol Sci Med Sci 61:262–266
Biernacki C, Celeux G, Govaert G (2003) Choosing starting values for the EM algorithm for getting the highest likelihood in multivariate Gaussian mixture models. Comput Stat Data Anal 41:561–575
Breyer F, Costa-Font J, Felder S (2010) Ageing, health, and health care. Oxf Rev Econ Policy 26:674–690
Dean N, Raftery AE (2010) Latent class analysis variable selection. Ann Inst Stat Math 62:11–35
Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B 39:1–38
Fraley C, Raftery AE (2002) Model-based clustering, discriminant analysis, and density estimation. J Am Stat Assoc 97:611–631
Galasso V, Profeta P (2007) How does ageing affect the welfare state? Eur J Polit Econ 23:554–563
Goodman LA (1974) Exploratory latent structure analysis using both identifiable and unidentifiable models. Biometrika 61:215–231
Harel O, Schafer JL (2009) Partial and latent ignorability in missing-data problems. Biometrika 96:37–50
Hawes CH, Morris JN, Phillips CD, Fries BE, Murphy K, Mor V (1997) Development of the nursing home resident assessment instrument in the USA. Age Agening 26:19–25
Karlis D, Xekalaki E (2003) Choosing initial values for the EM algorithm for finite mixtures. Comput Stat Data Anal 41:577–590
Kass R, Raftery AE (1995) Bayes factors. J Am Stat Assoc 90:773–795
Kohler HP, Billardi FC, Ortega JA (2002) The emergence of lowest-low fertility in Europe during the 1990s. Popul Dev Rev 28:641–680
Lafortune L, Beland F, Bergman H, Ankri J (2009) Health status transitions in community-living elderly with complex care needs: a latent class approach. BMC Geriatr 9:6
Lattanzio F, Mussi C, Scafato E, Ruggiero C, Dell’Aquila G, Pedone C, Mammarella F, Galluzzo L, Salvioli G, Senin U, Carbonin PU, Bernabei R, Cherubini A (2010) Health care for older people in Italy: The U.L.I.S.S.E. project (un link informatico sui servizi sanitari esistenti per l’anziano—a computerized network on health care services for older people). J Nutr Health Aging 14:238–242
Lazarsfeld PF (1950) The logical and mathematical foundation of latent structure analysis. In: Stouffer SA, Suchman EA, Guttman L (eds) Measurement and prediction. Princeton University Press, New York
Lazarsfeld PF, Henry NW (1968) Latent structure analysis. Houghton Mifflin, Boston
Little RJA, Rubin DB (2002) Statistical analysis with missing data, 2nd edn. Wiley Series in Probability and Statistics, Wiley
Lu G, Copas JB (2004) Missing at random, likelihood ignorability and model completeness. Ann Stat 32:754–765
Magidson J, Vermunt JK (2001) Latent class factor and cluster models, bi-plots and related graphical displays. Sociol Methodol 31:223–264
Moran M, Walsh C, Lynch A, Coen RF, Coakley D, Lawlor BA (2004) Syndromes of behavioural and psychological symptoms in mild Alzheimer’s disease. Int J Geriatr Psychiatry 19:359–364
Morris J, Hawes C, Murphy K et al (1991) Resident assessment instrument training manual and resource guide. Eliot Press, Natick
Rubin DB (1976) Inference and missing data. Biometrika 63:581–592
Samejima F (1969) Estimation of latent ability using a response pattern of graded scores. Psychometrika: monograph supplement, vol 17. Psychometric Society, Richmond, p i-169
Samejima F (1996) Evaluation of mathematical models for ordered polychotomous responses. Behaviormetrika 23:17–35
Schwarz G (1978) Estimating the dimension of a model. Ann Stat 6:461–464
Vermunt JK, Magidson J (2002) Latent class cluster analysis. In: Hagenaars JA, McCutcheon AL (eds) Applied latent class analysis. Cambridge University Press, Cambridge
Acknowledgments
All authors acknowledge the financial support from Regione Umbria (IT). F. Bartolucci also acknowledges the financial support from the Grant RBFR12SHVV of the Italian Government (FIRB project “Mixture and latent variable models for causal inference and analysis of socio-economic data”).
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Bartolucci, F., Montanari, G.E. & Pandolfi, S. Item selection by latent class-based methods: an application to nursing home evaluation. Adv Data Anal Classif 10, 245–262 (2016). https://doi.org/10.1007/s11634-016-0232-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11634-016-0232-3
Keywords
- Bayesian information criterion
- Expectation-maximization algorithm
- Polytomous items
- Quality-of-life
- ULISSE project