1 Introduction

Many industrial applications consist of repeated execution of the same task over a finite duration. A generic example is a gantry robot executing a pick and place task where the sequence of operations is: 1) collect the payload from a fixed location, 2) transfer the payload over a finite duration, 3) place the payload at a fixed location or under synchronization on a moving conveyor, 4) return to the starting location and 5) repeat 1)–4) as many times as required or until a halt is required for maintenance or for other reasons. Each execution is known as a trial over the finite trial length. Once a trial is complete, all the information generated during execution is available for use in computing the control input for the next trial.

Iterative learning control (ILC) was developed for applications such as the gantry robot task briefly outlined above where previous trial information is used to compute the control input to be applied on the next trial. The basic idea is to improve performance from trial-to-trial and non-causal temporal information can be used provided it is generated in a previous trial. For example, at instant, say t, in trial k + 1, k ≥ 0, information at t + λ, λ > 0, on trial k can be used in the computation of the control input on subsequent trials. The use of such information is the main distinguishing feature of ILC.

The widely recognized starting point for ILC research is [1], which considered a simple first order linear servomechanism system for speed control of a voltage-controlled direct current servomotor. Since this first work, ILC has been broadened in breadth and depth, for recent overviews of the literature [2, 3]. Robust ILC design is an active topic lately[4–7]. Applications of ILC included batch-to-batch control[8, 9], traffic control[10, 11], point-to-point control[12], and positioning control[13–14].

In this paper, we exploit the natural 2D system structure of ILC where one direction of information is from trial-to-trial indexed by the subscript k and the other along a trial indexed by p. The first work on treating ILC in a 2D system setting is [15], where the Roesser state-space model is used. This initial work has been followed by extensions to deal with, e.g., uncertainty in the model of the dynamics and uncertain initial conditions at the start of each trial[16]. In [17], the 2D system setting for analysis and design has been extended to nonlinear batch processes operating in a series of piecewise affine operating regions and with industrial applications in mind, allowing the presence of constraints on the input and output.

Given that the trial length is finite by definition, a more natural model for ILC is a repetitive process[18]. These processes are characterized by a series of sweeps, termed as passes, through a set of dynamics defined over a fixed finite duration known as the pass length. In particular, a pass is completed and then the process is reset before the start of the next pass. On each pass, an output, termed the pass profile, is produced which acts as a forcing function on, and hence contributes to, the dynamics of the next pass profile.

Repetitive processes have their origins in the coal mining industry, references to the original work in the 1970s are given in [18], where coal is extracted by a cutting machine that makes repeated sweeps along the coal face. During any sweep, the machine rests on the previous pass profile, the height of the stone/coal interface above some datum line. The basic geometry confirms that coal cutting is a repetitive process and other physical examples are again discussed in [18] and the relevant cited references.

The explicit interaction between successive pass profiles in a repetitive process can lead to oscillations that increase in amplitude from pass-to-pass and these oscillations cannot be removed by standard control action. A stability theory for linear constant pass length repetitive processes has been developed[18] that, in essence, requires that a bounded initial pass profile produces a bounded sequence of pass profiles. This theory is based on an abstract model of the dynamics in a Banach space setting with the bounded property defined in terms of the norm of the Banach space to which the pass profile is assumed to belong. The repetitive process setting has been used to design ILC laws that have, in contrast to the 2D system based designs, been experimentally verified on a gantry robot[19, 20], where the necessary computations are linear matrix inequality (LMI) based.

In [21], the generalized Kalman-Yakubovich-Popov Lemma is used to develop ILC design algorithms in the repetitive process setting where frequency attenuation, the physical interpretation of the stability property, is only imposed over finite frequency ranges selected by knowledge of the particular application, again with experimental verification. Also, the repetitive process setting has been used[22] to develop results on how to make the most effective use of previous trial information.

In operation, an ILC control law requires, as in other areas, that actuators and sensors function properly, where should a failure occur this can be total, in which case the overall control scheme may fail, or partial. One way to guard against such problems is to do a fault tolerant design[23]. This topic has already been the subject of productive research in ILC[24–26]. This paper contributes to this general area by using the repetitive process setting to analyze the effects of actuator faults, leading to LMI based control law design algorithms with an extension to both norm bounded and polytopic based robustness. A numerical case study is also given.

The next section gives the required background on repetitive processes and formulates the general problem considered, including the representation of the faults. Section 3 then considers nominal model based ILC design and Section 4 extends the analysis to norm bounded and polytopic uncertainty. In Section 5, a simulation based case study is given using the model of an electric motor system used for evaluating other ILC designs. Section 6 concludes the paper by giving an overview of the new results obtained and discussion of possible future research.

Throughout this paper, the null and identity matrices of compatible dimensions are denoted by 0 and I respectively. Also, X > 0 and X < 0 denote a symmetric positive definite matrix and a symmetric negative definite matrix, respectively. The symbol * represents transposed entries in a symmetric matrix and ρ(·) denotes the spectral radius of its matrix argument.

2 Background and problem formulation

Repetitive processes are characterized by a series of sweeps, termed passes, through a set of dynamics defined over a finite duration known as the pass length. On each pass, an output produced termed the pass profile and the sequence of operations is that a pass is completed and then the process resets to the starting location and the next pass can begin, either immediately or after some time has elapsed. The pass profile produced on the previous pass acts as forcing function on the next pass and hence contributes to its dynamics. Variables in a repetitive process are two dimensional functions and the notation used is of the form y k (p), 0 ≤ p ≤ α − 1, k ≥ 0, where y is the scalar or vector valued variable, α < ∞ is the pass length and the subscript k denotes the pass number.

Let {y k } denote the sequence of pass profiles generated by an example. Then, the control problem is that this sequence can contain oscillations that increase in amplitude from pass-to-pass, i.e., with k. Repetitive processes have their origins in the coal mining industry where coal is mined by a series of passes along the coal face by a cutting machine that rests on the previous pass profile during the completion of the next pass. The original references are in [18], and in this example, the oscillations in the pass profile sequence are due, in the main, to the weight of the cutting machine. In the absence of control action, the only option is to halt productive work to enable their manual removal.

Pass-to-pass oscillations generated by a repetitive process cannot be controlled by application of standard, or 1D, control system theory and design since such an approach ignores their 2D system structure, i.e., the finite pass length and the resetting of the initial conditions before the start of each new pass. A complete treatment of this aspect can be found in [18] and the relevant cited references.

A stability theory for linear constant pass length repetitive processes has been developed[18]. This is based on an abstract model in a Banach space setting that includes wide range of such linear repetitive processes. Given the control problem, this theory demands that a bounded initial pass profile produces as bounded sequence of pass profiles, with boundedness defined in terms of the norm on the underlying function space. Moreover, this property can be enforced over the finite and fixed pass length, termed asymptotic stability, or for all possible values of the finite pass length, termed stability along the pass. This last property can be analyzed by considering α → ∞ and this is the form of repetitive process stability required in this paper.

The ILC design in this paper is based on discrete linear repetitive processes whose state-space model over 0 ≤ p ≤ α − 1, k ≥ 0, is

$$\matrix{{{x_{k + 1}}(p + 1) = A{x_{k + 1}}(p) + B{u_{k + 1}}(p) + {B_0}{y_k}(p)} \hfill \cr{{y_{k + 1}}(p) = C{x_{k + 1}}(p) + D{u_{k + 1}}(p) + {D_0}{y_k}(p)} \hfill \cr}$$
(1)

where on pass k, x k (p) ∈ Rn is the state vector, y k (p) ∈ Rm is the pass profile vector and u k (p) ∈ Rr is the control input vector. The boundary conditions, i.e., the pass state initial vector sequence and the initial pass profile, are

$$\begin{array}{*{20}c} {x_{k + 1} (0) = d_{k + 1} ,} & {k \geqslant 0,} \\ {y_0 (p) = f(p),} & {0 \leqslant p \leqslant \alpha - 1} \\ \end{array} $$
(2)

where the vector functions dk+1 and f(p)haveknown entries. In this model, it is not assumed that the entries in dk+1 are the same for each k but they are independent of the previous pass dynamics. These boundary conditions are the simplest possible but applications do exist where they must be replaced by an alternative structure and, in particular, the entries of a state initial vector could be set as functions of sampling instants on each pass. This topic is also treated in [18] where the abstract model based theory shows that such state initial conditions alone can cause instability.

As discussed above, stability of these processes is defined in terms of the contribution of the previous pass profile to that on the next pass. For processes described by (1) and (2), the pass-to-pass coupling is described by the convolution operator, denoted by L α , for a standard linear system with state-space model matrices {A, B0, C, D0}. Hence the contribution from pass k to pass k + 1 can be written as yk+1 = L αyk , k ≥ 0. Also, let y k ∈ E α , where E α is a suitably chosen Banach space with norm denoted by ∥ · ∥ and let the same symbol denote the induced norm on the bounded linear operator L α .

Asymptotic stability for linear repetitive processes is equivalent to the existence of finite real scalars M α > 0 and λ α ∈ (0, 1) such that \(L_\alpha ^k \le {M_\alpha}\lambda _\alpha ^k,k \ge 0\). For examples, described by (1) and (2), asymptotic stability requires that ρ(D0) < 1 and if this condition holds, the sequence of pass profiles produced will converge in k to a standard discrete linear system, termed the limit profile, with state matrix A lp = A + B0(I − D0)−1 C. However, consider the special case when A = 0.5, B = 1, B0 = −0.5+ β, C =1 and D0 = 0. Then A lp = β and hence the limit profile is unstable in p, i.e., along the pass when ∣β∣ ≥ 1.

The existence of examples such as the one given above is due to the finite pass length, a property of the process and not an assumption imposed for analysis purposes. Stability along the pass prevents such examples from arising by imposing the stability property for all possible values of the finite pass length. This property requires the existence of finite real scalars existence of finite real scalars M ∞ > 0 and λ∞(0, 1), which are independent of α, such that \(L_\alpha ^k \le {M_\infty}\lambda _\infty ^k,k \ge 0\). The following result characterizes stability along the pass of examples described by (1) and (2).

  • Lemma 1[18]. A discrete linear repetitive process described by (1) and (2) is stable along the pass if and only if 1) ρ(D0) < 1, 2) ρ(A) < 1, and 3) all eigenvalues of G(z)= C(zI − A)−1 B0 + D0 have modulus strictly less than unity for all ∣z∣ = 1.

Note that the intuitively obvious condition 2) in this result is also only a necessary condition for stability along the pass as the simple example given above demonstrates. Condition 3) in this result requires frequency attenuation of the complete spectrum of the previous pass profile.

The systems considered in this paper have the following state-space model in the ILC setting

$$\matrix{{{x_k}(p + 1) = A{x_k}(p) + B{u_k}(p)} \hfill \cr{{y_k}(p) = C{x_k}(p)} \hfill \cr{{x_{k + 1}}(0) = {d_{k + 1}},\quad 0 \leq p \leq \alpha - 1} \hfill \cr}$$
(3)

where on trial k, x k (p) ∈Rn is the state vector, y k (p) ∈ Rm is the output vector, u k (p) ∈ Rr and the entries in dk++1 are known constants. Also let u k, i (p), 1 ≤ i ≤ r, denote the entries in u k (p)and let \(u_{k,i}^F(p)\) denote an input and actuator signal with possible failures. Then, the failure model used in this paper is[24]

$$u_{k,i}^F(p) = {\gamma _i}{u_{k,i}}(p),\;i = 1,2, \cdots ,r$$
(4)

where

$$0 \leq {\underline \gamma _i} \leq {\gamma _i} \leq {\bar \gamma _i},\;i = 1,2, \cdots ,r$$
(5)

The scalars \({\underline \gamma _i}({\underline \gamma _i} \ge 1)\) and \({\overline \gamma _i}({\overline \gamma _i} \ge 1)\) in this failure model are assumed to be known. The scalar γ i is unknown but assumed to vary within a known range. If \({\underline \gamma _i} = {\overline \gamma _i}\), the fault-free case is recovered, i.e., \(u_i^F = {u_i}\). Also, γ i = 0 is the case when the actuator experiences complete failure and γ i > 0 corresponds to a partial failure, i.e., partial degradation of the actuator.

Introduce the notation

$$\Gamma = {\rm{diag}}\{{\gamma _1},{\gamma _2}, \cdots ,{\gamma _r}\}$$
(6a)
$$\bar \Gamma = {\rm{diag}}\{{\bar \gamma _1},{\bar \gamma _2}, \cdots ,{\bar \gamma _r}\}$$
(6b)
$$\underline \Gamma = {\rm{diag}}\{{\underline \gamma _1},{\underline \gamma _2}, \cdots ,{\underline \gamma _r}\}$$
(6c)

to give

$$u_k^F = {[u_{k,1}^F,u_{k,2}^F, \cdots ,u_{k,r}^F]^{\rm{T}}} = \Gamma {u_k}.$$
(6d)

Hence, the system described by (3) with actuator faults of the form considered in this paper can be described by the state-space model

$$\matrix{{{x_k}(p + 1) = A{x_k}(p)B\Gamma {u_k}(p)} \hfill \cr{{y_k}(p) = C{x_k}(p)} \hfill \cr{{x_{k + 1}}(0) = {d_{k + 1}},\quad 0 \leq p \leq \alpha - 1.} \hfill \cr}$$
(7)

Also, let y r (p) denote the supplied reference vector. Then, the tracking error on trial k is

$${e_k}(p) = {y_r}(p) - {y_k}(p).$$
(8)

The control design problem is to determine a fault-tolerant ILC law such that trial-to-trial error convergence occurs in k, i.e., limk→∞ ∥e k ∥ =0, where ∥ · ∥ is a convenient norm, in the presence of actuator failures. Moreover, the control input applied on each trial must satisfy limk→∞ ∥u k − u ∞ ∥ = 0, where u∞ is termed the learned control.

The following structure for the computation of the current trial input permits the use of previous trial data

$${u_{k + 1}}(p) = {u_k}(p) + \Delta {u_{k + 1}}(p)$$
(9)

i.e., the control input on the previous trial plus a correction term Δu k +1(p). Introduce, for analysis purposes only,

$${\eta _{k + 1}}(p + 1) = {x_{k + 1}}(p) - {x_k}(p)$$
(10)

and set

$$\Delta {u_{k + 1}}(p) = {K_1}{\eta _{k + 1}}(p + 1) + {K_2}{e_k}(p + 1)$$
(11)

where K1 and K2 are compatibly dimensioned matrices to be designed. Then, the controlled dynamics can be reformulated as

$$\matrix{{{\eta _{k + 1}}(p + 1) = A{x_{k + 1}}(p - 1) + B\Gamma {u_{k + 1}}(p - 1) -} \hfill \cr{\quad \quad \quad \quad \quad A{x_k}(p - 1) - B\Gamma {u_k}(p - 1) =} \hfill \cr{\quad \quad \quad \quad \quad (A + B\Gamma {K_1}){\eta _{k + 1}}(p) + B\Gamma {K_2}{e_k}(p)} \hfill \cr{{e_{k + 1}}(p) = {y_d}(p) - {y_{k + 1}}(p) =} \hfill \cr{\quad \quad \quad \;{e_k}(p) + {y_k}(p) - {y_{k + 1}}(p) =} \hfill \cr{\quad \quad \quad \; - C(A + B\Gamma {K_1}){\eta _{k + 1}}(p) +} \hfill \cr{\quad \quad \quad \;(I - CB\Gamma {K_2}){e_k}(p)} \hfill \cr}$$
(12)

or

$$\matrix{{{\eta _{k + 1}}(p + 1) = \hat A{\eta _{k + 1}}(p) + \hat B{e_k}(p)} \hfill \cr{{e_{k + 1}}(p) = \hat C{\eta _{k + 1}}(p) + \hat D{e_k}(p)} \hfill \cr}$$
(13)

where

$$\matrix{{\hat A = A + B\Gamma {K_1},\hat B = B\Gamma {K_2},} \hfill \cr{\hat C = - C(A\Gamma {K_1}),\hat D = I - CB\Gamma {K_2}.} \hfill \cr}$$

The state-space model (13) is that of a discrete linear repetitive process of the form (1) with the input term deleted from both the state and pass profile updating equations. On trial k + 1, the ILC error e k +1(p) is the pass profile vector and ηk+1 (p) is the current state vector.

In the next section, repetitive process theory is applied to ILC design, where for the remainder of this paper, pass is used instead of trial to conform with repetitive process literature.

3 ILC design

Introduce the notation

$$\Sigma = {\rm{diag}}\{{\sigma _1},{\sigma _2}, \cdots ,{\sigma _r}\}$$
(14a)
$${\Sigma _0} = {\rm{diag}}\{{\sigma _{10}},{\sigma _{20}}, \cdots ,{\sigma _{r0}}\}$$
(14b)

with

$${\sigma _i} = {{{{\bar \gamma}_i} + {{\underline \gamma}_i}} \over 2},\;i = 1,2, \cdots ,r$$
(15a)
$${\sigma _{i0}} = {{{{\bar \gamma}_i} + {{\underline \gamma}_i}} \over {{{\bar \gamma}_i} + {{\underline \gamma}_i}}},\;i = 1,2, \cdots ,r.$$
(15b)

Also, from (6) and (15), an unknown matrix Γ0 exists such that

$$\Gamma = (I + {\Gamma _0})\Sigma$$
(16)

and

$$\vert {\Gamma _0}\vert \leq {\Sigma _0} \leq I$$
(17)

where

$${\Gamma _0} = {\rm{diag}}\{{\gamma _{10}},{\gamma _{20}}, \cdots ,{\gamma _{r0}}\}$$
(18)

and

$$\vert {\Gamma _0}\vert = {\rm{diag}}\{{\gamma _{10}}\vert ,\vert {\gamma _{20}}\vert , \cdots ,\vert {\gamma _{r0}}\} .$$

The analysis that follows will make extensive use of the Schur’s complement formula and the following result.

  • Lemma 2[27]. Assume X, Y, Z = ZT are real matrices with compatible dimensions. Then, for any matrix Δ satisfying ΔTΔ ≤ I, the inequality

    $$Z + X\Delta Y + {Y^{\rm{T}}}{\Delta ^{\rm{T}}}{X^{\rm{T}}} < 0$$

    holds if and only if there exists a positive scalar ε such that

    $$Z + \varepsilon X{X^{\rm{T}}} + {\varepsilon ^{- 1}}{Y^{\rm{T}}}Y < 0.$$

The conditions of Lemma 1 can be used to test the stability of the controlled dynamics (13) and also have well defined physical interpretations. In particular, condition 1) of this result shows that ILC pass-to-pass error convergence is independent of the state initial vector sequence assumed in this work. However, if the initial state vector is a function of points along the previous trial, e.g., xk+1(0) = dk++1 + L yk (α − 1), then repetitive process stability theory[18], shows this term alone can cause instability and hence pass-to-pass error divergence would occur. Condition 2) of Lemma 1 guarantees that state dynamics along any pass are bounded independent of the pass length and condition 3) imposes frequency attenuation over the complete spectrum of the previous pass error.

An alternative to Lemma 1 is to use a Lyapunov function-based interpretation of stability[18], which results in LMI based design where the computations to be completed involve only matrices with constant entries. This approach is based on a sufficient, but not necessary, set of stability conditions, but designs in this setting have been experimentally verified[19, 20]. The following is the first new result of this paper.

  • Theorem 1. The discrete linear repetitive process representation of the ILC dynamics (13) is stable along the pass if there exists a scalar λ > 0 and matrices X1 > 0, X2 > 0, R1 and R2 such that the following LMI is feasible:

    $$\left[ {\begin{array}{*{20}c} { - X_1 } & * & * & * & * \\ 0 & { - X_2 } & * & * & * \\ {AX_1 + B\Sigma R_1 } & {B\Sigma R_2 } & { - X_1 + \lambda B\Sigma _0^2 B^T } & * & * \\ { - CAX_1 - CB\Sigma R_1 } & {X_2 - CB\Sigma R_2 } & { - \lambda CB\Sigma _0^2 B^T } & { - X_2 + \lambda CB\Sigma _0^2 B^T C^T } & * \\ {\Sigma R_1 } & {\Sigma R_2 } & 0 & 0 & { - \lambda I} \\ \end{array} } \right] < 0.$$
    (19)

    If this LMI is feasible, the control law matrices K1 and K2 can be computed using

    $$\matrix{{{K_1} = {R_1}X_1^{- 1}} \hfill \cr{{K_2} = {R_2}X_2^{- 1}.} \hfill \cr}$$
    (20)

  • Proof. Consider the candidate Lyapunov function

    $${V_k}(p) = V_k^1(p) + V_k^2(p)$$
    (21)

    where

    $$\matrix{{V_2^1(p) = \eta _{k + 1}^{\rm{T}}(p){P_1}{\eta _{k + 1}}(p)} \hfill \cr{V_k^2(p) = e_k^{\rm{T}}(p){P_2}{e_k}(p).} \hfill \cr}$$

    with P i > 0, i = 1, 2 and increment

    $$\Delta V_k (p) = \Delta V_k^1 (p) + \Delta V_k^2 (p) = V_k^1 (p + 1) - V_k^1 (p) + V_{k + 1}^2 (p) - V_k^2 (p) = \left[ {\begin{array}{*{20}c} {\eta _{k + 1(p)}^T } & {e_k^T (p)} \\ \end{array} } \right] \times \left( {\Phi ^T P\Phi - P} \right)\left[ {\begin{array}{*{20}c} {\eta _{k + 1} (p)} \\ {e_k (p)} \\ \end{array} } \right]$$
    (22)

    where \(\Phi = \left[ {\begin{array}{*{20}c} {\hat A} & {\hat B} \\ {\hat C} & {\hat D} \\ \end{array} } \right]\), P = diag{P1, P2}. Then, (13) is stable along the pass if there exists P > 0 such that

    $${\Phi ^{\rm{T}}}P\Phi - P < 0.$$
    (23)

An obvious application of the Schur’s complement formula to (23) yields

$$\left[ {\begin{array}{*{20}c} { - P_1 } & * & * & * \\ 0 & { - P_2 } & * & * \\ {\hat A} & {\hat B} & { - P_1^{ - 1} } & * \\ {\hat C} & {\hat D} & 0 & { - P_2^{ - 1} } \\ \end{array} } \right] < 0.$$
(24)

Next, introduce

$${X_1} = P_1^{- 1},\quad {X_2} = P_2^{- 1}$$

and pre-(left) and post-(right) multiply (24) by diag{X1, X2, I, I} to obtain

$$\left[ {\begin{array}{*{20}c} { - X_1 } & * & * & * \\ 0 & { - X_2 } & * & * \\ {AX_1 + B\Gamma K_1 X_1 } & {B\Gamma K_2 X_2 } & { - X_1 } & * \\ { - CAX_1 - CB\Gamma K_1 X_1 } & {X_2 - CB\Gamma K_2 X_2 } & 0 & { - X_2 } \\ \end{array} } \right] < 0.$$
(25)

Also, from (16),

$$\Lambda + H{\Gamma _0}F + {F^{\rm{T}}}\Gamma _0^{\rm{T}}{H^{\rm{T}}} < 0$$
(26)

where

$$\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} { - X_1 } & * & * & * \\ 0 & { - X_2 } & * & * \\ {AX_1 + B\Sigma K_1 X_1 } & {B\Sigma K_2 X_2 } & { - X_1 } & * \\ { - CAX_1 - CB\Sigma K_1 X_1 } & {X_2 - CB\Sigma K_2 X_2 } & 0 & { - X_2 } \\ \end{array} } \right]} \\ {H = \left[ {\begin{array}{*{20}c} 0 & 0 & {B^T } & { - B^T C^T } \\ \end{array} } \right]^T } \\ {F = \left[ {\begin{array}{*{20}c} {\Sigma K_1 X_1 } & {\Sigma K_2 X_2 } & 0 & 0 \\ \end{array} } \right].} \\ \end{array} $$

From Lemma 2, it follows that (26) holds if there exists a positive scalar λ > 0 such that

$$\Lambda + \lambda H\Sigma _0^2{H^{\rm{T}}} + {\lambda ^{- 1}}{F^{\rm{T}}}F < 0.$$
(27)

Using the Schur’s complement formula, (27) is equivalent to

$$\left[ {\begin{array}{*{20}c} {\Lambda + \lambda H\Sigma _0^2 H^T } & * \\ F & { - \lambda I} \\ \end{array} } \right] < 0.$$
(28)

Finally, introducing

$${R_1} = {K_1}{X_1},\quad {R_2} = {K_2}{X_2}$$

completes the proof. □

4 Robustness

4.1 Norm bounded uncertainty

Consider the following discrete-time linear system in the ILC setting with actuator faults and possibly time-varying uncertainties

$$\matrix{{{x_k}(p + 1) = (A + \Delta A){x_k}(p) + B\Gamma {u_k}(p)} \hfill \cr{{y_k}(p) = C{x_k}(p)} \hfill \cr{{x_{k + 1}}(0) = {d_{k + 1}},\quad 0 \leq p \leq \alpha - 1} \hfill \cr}$$
(29)

where ΔA represents admissible uncertainties that are assumed to satisfy

$$\Delta A = {H_1}\Delta {F_1}$$
(30)

where H1 and F1 are known constant matrices of appropriate dimensions and Δ is an unknown constant matrix or a matrix function satisfying

$${\Delta ^{\rm{T}}}\Delta \leq I.$$
(31)

Using (9)–(11) and following the analysis of the previous section, the controlled ILC dynamics with faults are described by the uncertain discrete linear repetitive process state-space model

$$\matrix{{{\eta _{k + 1}}(p + 1) = (\hat A + \Delta \hat A){\eta _{k + 1}}(p) + \hat B{e_k}(p)} \hfill \cr{{e_{k + 1}}(p) = (\hat C + \Delta \hat C){\eta _{k + 1}}(p) + \hat D{e_k}(p)} \hfill \cr}$$
(32)

where \(\Delta \hat A = \Delta A\) and \(\Delta \hat C = - C\Delta A\).

  • Theorem 2. The discrete linear repetitive process representation of the ILC dynamics (32) is stable along the pass if there exist scalars λ > 0, ϵ > 0and matrices X1 > 0, X2 > 0, R1, R2 such that the following LMI is feasible:

    $$\left[ {\begin{array}{*{20}c} { - X_1 } & * & * & * & * & * & * \\ 0 & { - X_2 } & * & * & * & * & * \\ {AX_1 + B\Sigma R_1 } & {B\Sigma R_2 } & { - X_1 + \lambda B\Sigma _0^2 B^T } & * & * & * & * \\ { - CAX_1 - CB\Sigma R_1 } & {X_2 - CB\Sigma R_2 } & { - \lambda CB\Sigma _0^2 B^T } & { - X_2 + \lambda CB\Sigma _0^2 B^T C^T } & * & * & * \\ {\Sigma R_1 } & {\Sigma R_2 } & 0 & 0 & { - \lambda I} & * & * \\ 0 & 0 & {\varepsilon H_1^T } & { - \varepsilon H_1^T C^T } & * & { - \varepsilon I} & * \\ {F_1 X_1 } & 0 & 0 & 0 & * & 0 & { - \varepsilon I} \\ \end{array} } \right] < 0.$$
    (33)

    If this LMI is feasible, the control law matrices K1 and K2 are given by \({K_1} = {R_1}X_1^{- 1}\) and \({K_2} = {R_2}X_2^{- 1}\).

  • Proof. In addition to the proof for Theorem 1, it is required to show that

    $$\Pi + H\Delta F + {F^{\rm{T}}}{\Delta ^{\rm{T}}}{H^{\rm{T}}} < 0$$
    (34)

    where

    $$\begin{array}{*{20}c} {\Pi = \left[ {\begin{array}{*{20}c} { - X_1 } & * & * & * & * \\ 0 & { - X_2 } & * & * & * \\ {AX_1 + B\Sigma R_1 } & {B\Sigma R_2 } & { - X_1 + \lambda B\Sigma _0^2 B^T } & * & * \\ { - CAX_1 - CB\Sigma R_1 } & {X_2 - CB\Sigma R_2 } & { - \lambda CB\Sigma _0^2 B^T } & { - X_2 + \lambda CB\Sigma _0^2 B^T C^T } & * \\ {\Sigma R_1 } & {\Sigma R_2 } & 0 & 0 & { - \lambda I} \\ \end{array} } \right]} \\ {H = \left[ {\begin{array}{*{20}c} 0 & 0 & {H_i^T } & { - H_1^T C^T } & 0 \\ \end{array} } \right]^T } \\ {F = \begin{array}{*{20}c} {F_1 X_1 } & 0 & 0 & 0 & 0 \\ \end{array} .} \\ \end{array} $$

From Lemma 2, it follows that (34) holds for all Δ satisfying (31) if there exists a positive scalar ϵ > 0 such that

$$\Pi + \epsilon H{H^{\rm{T}}} + {\epsilon ^{- 1}}{F^{\rm{T}}}F < 0$$
(35)

which, on applying the Schur’s complement formula, is equivalent to

$$\left[ {\begin{array}{*{20}c} \Pi & * \\ {\left[ {\begin{array}{*{20}c} {\varepsilon ^{\tfrac{1} {2}} H^T } \\ {\varepsilon ^{ - \tfrac{1} {2}} F} \\ \end{array} } \right]} & { - I} \\ \end{array} } \right] < 0.$$
(36)

Finally pre-multiplying and post-multiplying (36) by \({\rm{diag}}\{I,I,I,I,I,{\epsilon^{{1 \over 2}}}I,{\epsilon^{{1 \over 2}}}I\}\) gives the LMI of (33). □

4.2 Polytopic uncertainty

Polytopic uncertainty assumes that the matrices defining the system state-space model lie in a convex bounded uncertain domain Ω of the form

$$\matrix{{\Omega = \left\{{\left[ {A\left({\xi (k,p)} \right),B\left({\xi (k,p)} \right)} \right]\left\vert {\left[ {A\left({\xi (k,p)} \right),B\left({\xi (k,p)} \right)} \right]} \right. =} \right.} \hfill \cr{\left. {\quad \quad \sum\limits_{i = 1}^N {{\xi _i}(k,p)({A_i},{B_i}),{\xi _i} \geq 0,\sum\limits_{i = 1}^N {{\xi _i}(k,p) = 1}}} \right\}} \hfill \cr}$$
(37)

where A i , B i are the corresponding matrix vertices and N denotes their number.

The uncertain discrete linear repetitive process model for ILC in the presence of polytopic uncertainty is

$$\matrix{{{\eta _{k + 1}}(p + 1) = \hat A\left({\xi (k,p)} \right){\eta _{k + 1}}(p) + \hat B\left({\xi (k,p)} \right){e_k}(p)} \hfill \cr{{e_{k + 1}} = \hat C\left({\xi (k,p)} \right){\eta _{k + 1}}(p) + \hat D\left({\xi (k,p)} \right){e_k}(p)} \hfill \cr}$$
(38)

where

$$\matrix{{\hat A\left({\xi (k,p)} \right) = A\left({\xi (k,p)} \right) + B\left({\xi (k,p)} \right)\Gamma {K_1}} \hfill \cr{\hat B\left({\xi (k,p)} \right) = B\left({\xi (k,p)} \right)\Gamma {K_2}} \hfill \cr{\hat C\left({\xi (k,p)} \right) = - C\left[ {A\left({\xi (k,p)} \right) + B\left({\xi (k,p)} \right)\Gamma {K_1}} \right]} \hfill \cr{\hat D\left({\xi (k,p)} \right) = I - CB\left({\xi (k,p)} \right)\Gamma {K_2}.} \hfill \cr}$$

  • Theorem 3. The repetitive process representing the ILC dynamics (38) is stable along the pass if there exists a scalar λ > 0 and matrices X1 > 0, X2 > 0, R1, R2 such that the following LMI is feasible:

    $$\left[ {\begin{array}{*{20}c} { - X_1 } & * & * & * & * \\ 0 & { - X_2 } & * & * & * \\ {A_i X_1 + B_i \Sigma R_1 } & {B_i \Sigma R_2 } & { - X_1 + \lambda B_i \Sigma _0^2 B_i^T } & * & * \\ { - CA_i X_1 - CB_i \Sigma R_1 } & {X_2 - CB_i \Sigma R_2 } & { - \lambda CB_i \Sigma _0^2 B_i^T } & { - X_2 + \lambda CB_i \Sigma _0^2 B_i^T C^T } & * \\ {\Sigma R_1 } & {\Sigma R_2 } & 0 & 0 & { - \lambda I} \\ \end{array} } \right] < 0$$
    (39)

    for i = 1, 2, ⋯, N.

    If this LMI is feasible, the control law matrices K1 and K2 are given by \({K_1} = {R_1}X_1^{- 1}\) and \({K_2} = {R_2}X_2^{- 1}\).

  • Proof. The uncertain process is stable along the pass if this property holds for every vertex. The proof now follows identical steps to that of Theorem 1 for each matrix vertex. □

5 Case study

Consider the following model of an electric motor system given in [22] and references therein

$$\begin{array}{*{20}c} {\dot x(t) = A_c x(t) + B_c u(t)} \\ {y(t) = C_c x(t)} \\ \end{array} $$
(40)

where

$$\begin{array}{*{20}c} {A_c = \left[ {\begin{array}{*{20}c} { - \tfrac{{V_B }} {J}} & { - \tfrac{{3n_p \varphi _{mg} }} {{2J}}} & 0 \\ 0 & { - \tfrac{1} {\gamma }} & 0 \\ {\tfrac{{\omega _b }} {{2\pi }}} & {0.81} & 0 \\ \end{array} } \right]} \\ {B_c = \left[ {\begin{array}{*{20}c} 0 \\ {\tfrac{1} {\gamma }} \\ 0 \\ \end{array} } \right]} \\ {C_c = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right]} \\ \end{array} $$

with the following nominal motor parameters

$$\matrix{{{V_B} = 0.0625,\;J = 0.0267,\;{n_p} = 2} \hfill \cr{\gamma = 0.8 \times {{10}^{- 4}},\;{\phi _{mg}} = 0.9102,\;{\omega _b} = 315.315.} \hfill \cr}$$
(41)

Also, this model has been sampled at T s = 0.02 s to give a state-space model of the form (3). The pass length is 2s, the reference signal is

$${y_r}(t) = \sin (\pi t) + 0.5\sin (2\pi t) + 0.5\sin (3\pi t)$$
(42)

and zero boundary conditions are assumed. Also, pass-to-pass error convergence is measured by the root mean square formula

$$ER(k) = \sqrt {{1 \over \alpha}\sum\limits_{p = 0}^{\alpha - 1} {e_k^{\rm{T}}(p){e_k}(p)}} .$$
(43)

Assume that there exists an unknown actuator fault Γ but it is known that \(0.7 = \underline \Gamma \le \Gamma \le \overline \Gamma = 1.3\), and hence from (14) and (15), ∑ = 1, ∑0 = 0.3. The design is now illustrated by considering different scenarios of faults and uncertainty.

5.1 Scenario 1: Constant fault and nominal model

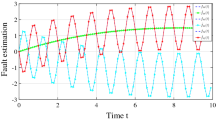
The controlled nominal process has been simulated with Γ = 1.3until k = 20 when a constant fault caused a switch to Γ = 0.7, and then at k = 40, a further switch returned Γ to its starting value.

Application of Theorem 1 results in the control law matrices given in the first row of Table 1. The simulation results for the controlled dynamics are shown in Fig. 1.

Fig. 1
figure 1

Simulation results for the Scenario 1 design

Full size image
Table 1 Control law matrices
Full size table

5.2 Scenario 2: Time-varying fault and model with norm-bounded uncertainties

The controlled processes with norm-bounded uncertainty has been simulated with Γ = 0.7until k = 20 when the constant fault switched to the time-varying fault Γ = 1 + 0.3sin(p), and then at k = 40, a further switch to Γ = 1 + 0.3cos(p) occurred. The matrices defining the uncertainty were taken as H1 = diag{0.1, 0.1, −0.05}, F1 = I and Δ = diag{δ1, δ2, δ3}, where δ1, δ2 and δ3 vary randomly between −1 and 1. Application of Theorem 2 gave the control law matrices shown in the second row of Table 1. The simulation results for the controlled dynamics are shown in Fig. 2.

Fig. 2
figure 2

Simulation results for the Scenario 2 design

Full size image

5.3 Scenario 3: Time-varying fault and model with polytopic uncertainties

In the motor model, ϕ mg and J are considered as uncertain parameters of the form

$$\matrix{{{\phi _{mg}} = {\xi _1}{\phi _{mg1}} + {\xi _2}{\phi _{mg2}}} \hfill \cr{J = {\xi _1}{J_1} + {\xi _2}{J_2}} \hfill \cr}$$
(44)

where (ϕ mg 1, J1) = (0.5, 0.016), (ϕ mg 2, J2) = (1.5, 0.036), ξ1 + ξ2 = 1, ξ1 and ξ2 are uncertain variables lying within [0, 1].

This gives a polytopic uncertainty with two vertices defined by the matrices:

  • Vertex 1:

    $$\begin{array}{*{20}c} {A_1 = \left[ {\begin{array}{*{20}c} {0.9248} & {0.0591} & 0 \\ 0 & 0 & 0 \\ {0.9655} & {0.595} & 1 \\ \end{array} } \right],} & {B_1 } \\ \end{array} = \left[ {\begin{array}{*{20}c} {86.9355} \\ 0 \\ {87.5465} \\ \end{array} } \right].$$

  • Vertex 2:

    $$\begin{array}{*{20}c} {A_2 = \left[ {\begin{array}{*{20}c} {0.9659} & {0.0822} & 0 \\ 0 & 0 & 0 \\ {0.9865} & {0.08} & 1 \\ \end{array} } \right],} & {B_2 } \\ \end{array} = \left[ {\begin{array}{*{20}c} {120.8769} \\ 0 \\ {119.1818} \\ \end{array} } \right].$$

The controlled system has been simulated with (ϕ mg , J) = (0.5, 0.016) and Γ = 0.7until k = 20 when the parameters were switched to (ϕ mg , J) = (1.5, 0.036) and Γ = (1 + 0.3sin(p)), and finally at k = 40, a further switch occurs to (ϕmg, J) = (0.5, 0.016) and Γ = (1 + 0.3cos(p)). Application of Theorem 3 gave the control law matrices shown in the third row of Table 1. The simulation results for the controlled dynamics are shown in Fig. 3.

Fig. 3
figure 3

Simulation results for the Scenario 3 design

Full size image

From Figs. 1–3, it is seen that the tracking performance along the pass direction experiences degradation when the value of fault changes at k =20and k = 40. However, the tracking performance quickly recovers over subsequent passes.

Given the control law matrices K1 and K2, the control law for implementation on pass k can, after routine manipulations of (9), be written as

$$\matrix{{{u_k}(p) = {u_{k - 1}}(p) + {K_1}\left({{x_k}(p) - {x_{k - 1}}(p) +} \right)} \hfill \cr{\quad \quad \quad {K_3}\left({{y_r}(p + 1) - {y_{k - 1}}(p + 1)} \right)} \hfill \cr}$$
(45)

where the second term on the right-hand side is phase-lead ILC, i.e., information that is non-causal in the temporal domain. The first term on the right-hand side is activated by the difference in the state vectors on two successive passes and an obvious extension is to seek to replace the state vectors with their pass profile counterparts. Finally, there are alternative 2D systems based designs that could be employed, e.g., [28], but the form of the control law to be implemented is much less transparent in terms of actual implementation. Moreover, the analysis in [22] uses a repetitive process model that has no 2D discrete linear systems counterpart. Finally, the repetitive process setting for design can be undertaken for differential dynamics, i.e., where design by emulation is the preferred or only option for a given application. This uses the theory of differential repetitive processes and again there is no 2D systems model counterpart or lifted model. In comparison to [24], the major advance in this paper is the robustness analysis and control law design.

6 Conclusions

This paper has considered the relevant applications problem of ILC design in the presence of actuator faults. The new results have been derived by writing the dynamics in each case as a discrete linear repetitive process, resulting in LMI based computations. It has also been shown that the results extend in a natural manner to norm bounded and polytopic uncertainty. The performance has been illustrated by a simulation case study on an electric motor system used in other ILC designs. These results provide a firm basis for onward development and eventual experimental verification.